БАЗОВІ ЗАДАЧІ, ЯКІ МОЖНА ПРОПОНУВАТИ УЧНЯМ ПРИ РОЗВ’ЯЗУВАННІ ЧОТИРИКУТНИКІВ
БАЗОВІ ЗАДАЧІ, ЯКІ МОЖНА ПРОПОНУВАТИ УЧНЯМ ПРИ РОЗВ’ЯЗУВАННІ ЧОТИРИКУТНИКІВ, А ТАКОЖ ПРИКЛАДИ ЗАДАЧ, ЩО РОЗВ’ЯЗУЮТЬСЯ З ЇХ ЗАСТОСУВАННЯМ.
Відмітимо деякі властивості чотирикутників, які часто застосовуються при розв’язуванні задач:
-
Сума внутрішніх кутів чотирикутника дорівнює
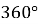
- Якщо з’єднати послідовно середини всіх сторін довільного чотирикутника ,то отримаємо паралелограм.
Доведення цих властивостей очевидне .
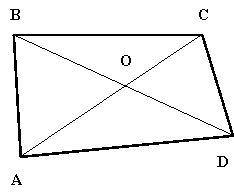
Базова задача 1. Довести, що площа будь-якого чотирикутника дорівнює половині добутку його діагоналей, помноженому на синус кута між ними:
![]() ,
,
де S – площа чотирикутника, d1 і d2 – довжини його діагоналей, ![]() - величина кута між діагоналями чотирикутника.
- величина кута між діагоналями чотирикутника.
![]()
![]()
Доведення:
Нехай в чотирикутника ABCD діагоналі АС і ВС дорівнюють d1 і d2 відповідно, a ![]() . Знайдемо площі кожного трикутника, на які діагоналі розділили даний чотирикутник:
. Знайдемо площі кожного трикутника, на які діагоналі розділили даний чотирикутник:
![]() ,
,
![]()
![]() .
.
Аналогічно
![]() ,
, ![]() .
.
Додамо ліві і праві частини даних рівностей:
![]()
![]()
![]()
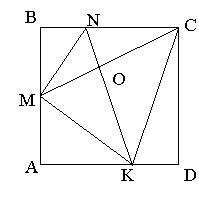
Задача 1.1 На сторонах квадрата ABCD дано точки М, N і К, де М – середина AB, N належить стороні ВС, причому 2BN=NC, К належить стороні DA, причому 2DK=КА. Знайти синус кута між МС і NK.
Розв’язання:
Нехай ![]() і
і ![]()
Обчислимо площі трикутників
![]() ,
,
![]() ,
,
![]() .
.
Тоді
![]()
![]() (*)
(*)
Неважко обчислити діагоналі МС і NK чотирикутника MNCK:
![]() ,
, ![]() .
.
Знайдемо ![]() за формулою базової задачі 1:
за формулою базової задачі 1:
![]() (**)
(**)
Прирівняємо праві частини рівностей (*) і (**)
![]()
![]() .
.
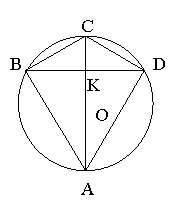
Задача 1.2 В коло вписано чотирикутник з кутами 120°, 90°, 60°, 90°. Площа чотирикутника дорівнює
![]() см2. Знайти радіус кола, якщо діагоналі чотирикутника взаємно перпендикулярні.
см2. Знайти радіус кола, якщо діагоналі чотирикутника взаємно перпендикулярні.
![]()
Розв’язання:
Нехай ABCD даний чотирикутник вписаний в коло, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() . За висновком базової задачі 1
. За висновком базової задачі 1
![]() ,
,
![]() ,
,
![]() (*)
(*)
Нескладно довести, що ![]() і
і ![]() –рівнобедрені, отже
–рівнобедрені, отже ![]() ,
, ![]() .
.
Позначимо ![]() , тоді
, тоді ![]() ,
,
![]() ,
, ![]() . Підставимо довжини діагоналей у рівність (*):
. Підставимо довжини діагоналей у рівність (*):
![]() ,
,
![]() ,
,
![]() ,
,
Базова задача 2. Довести, що якщо в чотирикутник вписано (або можна вписати) коло, то суми довжин його протилежних сторін рівні.
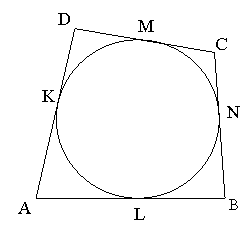
Доведення: Розглянемо чотирикутник ABCD, в який вписано коло. Нехай К, L, М, N – точки дотику чотирикутника і кола.
Тоді ![]()
(відрізки дотичних, проведених з відповідних точок).
Звідси:
![]() ,
,
т. б. ![]() .
.
Задача 2.1 Навколо кола описана рівнобічна трапеція з бічною стороною l, одна з основ якої дорівнює а. Знайти площу трапеції.

Розв’зання:
Нехай ABCD – дана трапеція, у якої AD=a, AB=l. Із властивості описаного навколо кола чотирикутника знаходимо, що ![]()
Побудуємо![]() ,
,
![]() .
.
З ![]() :
: ![]() .
.
Звідси: ![]() .
.
Задача 2.2. Пряма, перпендикулярна до двох сторін паралелограма, ділить його на дві трапеції, в кожну з яких можна вписати коло. Знайти гострий кут паралелограма, якщо довжини його сторін дорівнюють a i b (a < b).
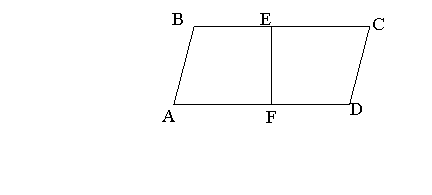
Розв’язання:
Нехай у паралелограма ABCD AB=a, AD=b і пряма EF перпендикулярна до AD і BC. Згідно умови в кожну з отриманих прямокутних трапецій можна вписати коло.
Нескладно довести, що ![]() .
.
Нехай ![]() і
і ![]() .
.
Тоді ![]() і
і ![]() .
.
За властивістю базової задачі 2 маємо
![]() ,
,
![]() ,
,
![]() ,
, ![]() .
.
Базова задача 3. В трапеції ABCD основи AD і ВС відповідно дорівнюють а і b. Через точку Е, що належить стороні АВ, причому ![]() , проведено пряму, паралельну основам трапеції, яка перетинає сторону CD в
, проведено пряму, паралельну основам трапеції, яка перетинає сторону CD в
точці F. Довести, що ![]() .
.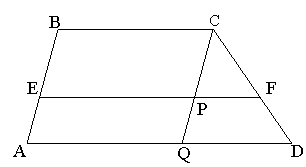
Доведення: Через вершину трапеції С проведемо пряму, паралельну стороні АВ, яка перетинає прямі EF і AD в точках Р і Q відповідно. Зрозуміло, що
![]() і
і ![]() .
.
![]() , а значить
, а значить ![]() ,
,
т.б. ![]() , звідки
, звідки ![]() .
.
Задача 3.1 Пряма, паралельна основам трапеції, проходить через точку перетину її діагоналей. Знайти довжину відрізка цієї прямої, розташованого між бічними сторонами трапеції, якщо основи трапеції дорівнюють
4 см і 12 см.
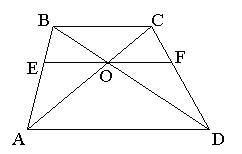
Розв’язання:
В трапеції ABCD AD=12 см і ВС=4см. Через точку О – точку перетину діагоналей проведемо пряму, паралельну основам трапеції, яка перетинає сторони АВ і CD в точках Е і F відповідно.
![]() ;
; ![]()
У такому ж відношенні точка Е ділить АВ т. б.
![]() , тоді, використовуючи твердження базової задачі 3, маємо:
, тоді, використовуючи твердження базової задачі 3, маємо:
![]() .
.
Задача 3.2 Два кола радіусами ![]() і
і ![]() дотикаються зовнішнім дотиком. Знайти відстань від точки дотику кіл до їх спільних дотичних.
дотикаються зовнішнім дотиком. Знайти відстань від точки дотику кіл до їх спільних дотичних.
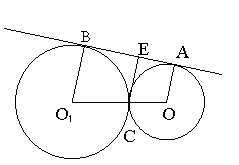
Розв’язання:
Нехай радіуси кіл з центрами О і О1, які дотикаються в точці С , дорівнюють 1 см і 3 см відповідно. Проведемо радіуси ОА і О1В в точки дотику кіл до їх спільної зовнішньої дотичної.
ОАВО1 – прямокутна трапеція. З точки С опустимо перпендикуляр СЕ на АВ. СЕ – шукана відстань.
Оскільки СЕ паралельний основам трапеції ОАВО1, то згідно формули базової задачі 3, маємо:
![]() .
.
Зрозуміло, що така ж буде і відстань від точки С до другої спільної зовнішньої дотичної.
Базова задача 4. Довести, що у рівнобічній трапеції, перпендикуляр, проведений з вершини меншої основи до більшої, ділить її на частини, більша з яких дорівнює по довжині середній лінії трапеції.
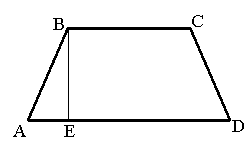
Доведення: Нехай ABCD – рівнобічна трапеція (![]() ) і AB=CD. Побудуємо
) і AB=CD. Побудуємо ![]() .
.
![]() , тоді
, тоді
![]() .
.
Задача 4.1 Навколо трапеції ABCD описане коло, діаметром якого є основа AD, що дорівнює а. Діагональ трапеції АС дорівнює l. Знайти площу трапеції.
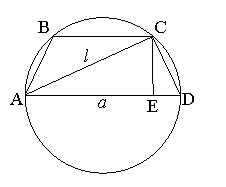
Розв’язання:
Так як навколо трапеції описане коло, то вона рівнобічна. Згідно умови, AD – діаметр описаного кола, тому ![]() – прямокутний. Проведемо
– прямокутний. Проведемо ![]() . Згідно твердження, доведеного в базовій задачі 4, довжина АЕ дорівнює довжині середньої лінії.
. Згідно твердження, доведеного в базовій задачі 4, довжина АЕ дорівнює довжині середньої лінії.
З ![]() ,
,
![]() ,
,
З ![]() ,
,
![]() .
.
Задача 4.2 Знайти площу рівнобічної трапеції, якщо її більша основа, діагональ і бічна сторона дорівнюють 4; 3 і 2 відповідно.
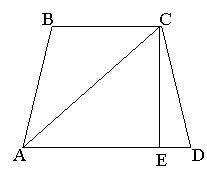
Розв’язання:
У рівнобічній трапеції ABCD ![]() більша основа
більша основа ![]() , діагональ
, діагональ ![]() і бічна сторона
і бічна сторона ![]() . Побудуємо
. Побудуємо ![]() . За формулою Герона обчислимо площу
. За формулою Герона обчислимо площу ![]() .
.
![]()
З іншого боку ![]() ,
,
Або ![]() ,
, ![]() .
.
З ![]() .
.
Використовуючи твердження базової задачі 4, отримаємо:
![]() .
.
Базова задача 5. Довести, що якщо діагоналі рівнобічної трапеції взаємно перпендикулярні, то довжина висоти трапеції дорівнює довжині середньої лінії, а площа дорівнює квадрату її висоти.
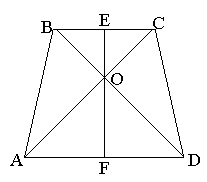
Доведення:
Нехай ABCD — рівнобічна трапеція, діагоналі якої АС і BD взаємно перпендикулярні. Через точку перетину діагоналей О проведемо висоту трапеції EF. З того, що трапеція рівнобічна, випливає, що ΔAOD і ΔВОС – рівнобедрені. Але оскільки вони ще й прямокутні, то
![]() .
.
Додамо ці рівності:
![]() ,
,
![]() ,
,
значить ![]() .
.
Задача 5.1 Площа рівнобічної трапеції, діагоналі якої взаємно перпендикулярні, дорівнює S. Знайти периметр цієї трапеції, якщо її бічна сторона утворює з більшою основою кут α.
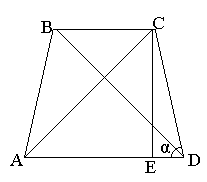
Розв’язання:
Нехай ABCD – рівнобічна трапеція. Побудуємо ![]() . Оскільки діагоналі трапеції взаємно перпендикулярні, то
. Оскільки діагоналі трапеції взаємно перпендикулярні, то
![]() .
.
З ![]() :
: ![]() .
.
Отже:
![]() .
.
Задача 5.2 У рівнобічної трапеції середня лінія дорівнює m, а діагоналі взаємно перпендикулярні . Обчислити площу трапеції.

Розв’язання:
Нехай ABCD – рівнобічна трапеція (![]() ). Середня лінія якої дорівнює m,
). Середня лінія якої дорівнює m, ![]() . За висновком базової задачі 5 висота даної трапеції дорівнює m, а площа m2.
. За висновком базової задачі 5 висота даної трапеції дорівнює m, а площа m2.
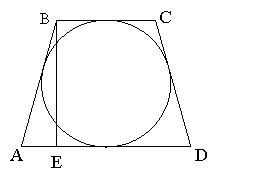 Базова задача 6. Довести, що якщо в рівнобічну трапецію можна вписати коло, то висота трапеції є середнє геометричне її основ.
Базова задача 6. Довести, що якщо в рівнобічну трапецію можна вписати коло, то висота трапеції є середнє геометричне її основ.
Доведення: Нехай ABCD - рівнобічна трапеція, в яку вписано коло . Побудуємо ![]() . Нехай
. Нехай ![]() ,
, ![]() ,
, ![]() . За властивістю, доведеною в базовій задачі 2,
. За властивістю, доведеною в базовій задачі 2, ![]() . Як уже відзначалось
. Як уже відзначалось ![]() .
.
З ![]() :
:
![]() ,
,
отже ![]() .
.
Задача 6.1 Навколо кола радіусом 5 см описана рівнобічна трапеція . Відстань між точками дотику бічних сторін дорівнює 8 см . Знайти площу трапеції.
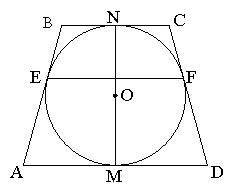
Розв’язання:
Навколо кола з центром О описана рівнобічна трапеція ABCD (![]() ), яка дотикається кола в точках Е, N, F, М. За умовою
), яка дотикається кола в точках Е, N, F, М. За умовою ![]() ,
, ![]() .
.
Оскільки точки Е і F рівновіддалені від основи AD трапеції, то ![]() .
.
Нехай ![]() і
і ![]() ,
,
тоді ![]() ,
, ![]() .
.
Використовуючи висновок базової задачі 6, маємо:
![]() , т. б.
, т. б. ![]() або
або ![]() .
.
Використавши результат базової задачі 3, отримаємо:
![]() ;
;
![]() , або
, або ![]() ,
, ![]() .
.
![]() .
.
Задача 6.2 В рівнобічну трапецію вписано коло радіусом R. Одна з основ трапеції у два рази менше її висоти. Знайти площу трапеції.
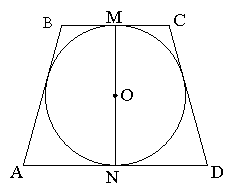
Розв’язання:
Нехай ABCD дана рівнобічна трапеція (![]() ), MN – висота трапеції,
), MN – висота трапеції, ![]() ,
, ![]() .
.
Так як ![]() , то
, то ![]() .
.
За висновком базової задачі 6:
![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.
Базова задача 7. Довести, що сума квадратів довжин діагоналей паралелограма дорівнює сумі квадратів довжин його сторін.
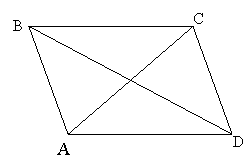
Доведення:
Нехай у паралелограма ABCD ![]() ,
,
тоді ![]() .
.
З ![]() за теоремою косинусів
за теоремою косинусів
![]() ,
,
3 ![]() аналогічно
аналогічно
![]()
![]() .
.
Додамо ці рівності:
![]() .
.
Задача 7.1 В трикутник вписано паралелограм зі сторонами 3 см і 5 см і діагоналлю 6 см. Знайти сторони трикутника, якщо відомо, що діагоналі паралелограма відповідно паралельні двом сторонам трикутника, а менша з його сторін лежить на третій стороні трикутника.
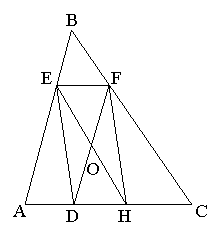
Розв’язання:
В паралелограмі DEFH, який вписано в трикутник ABC, ![]() ,
, ![]() ,
, ![]() . Нехай відповідно до умови
. Нехай відповідно до умови ![]() ,
, ![]() . Тоді очевидно, що
. Тоді очевидно, що ![]() і
і
![]() .
.
Знайдемо DF за допомогою результату базової задачі 7
![]()
![]()
Тоді![]()
Задача 7.2 Перпендикуляр, проведений з вершини паралелограма до його діагоналі, ділить цю діагональ на відрізки довжиною 6 см і 15 см. Різниця довжин сторін паралелограма дорівнює 7 см. Знайти довжини сторін паралелограма і його діагоналі.
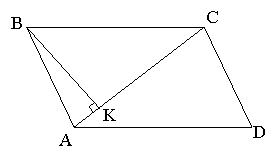
Розв’язання:
Нехай ABCD даний паралелограм, ![]() ,
, ![]() см,
см, ![]() см,
см, ![]() см.
см.
Позначимо ![]() , тоді
, тоді ![]() .
.
З ![]() :
: ![]() ,
,
з ![]() :
: ![]() .
.
Звідси:
![]() ,
,
![]() ,
,
![]() ,
,
тоді ![]() ,
,
![]()
Використовуючи твердження базової задачі 7, маємо: ![]()
![]()
![]() .
.
Відповідь: 10 см, 17 см, 21 см, ![]() см.
см.


про публікацію авторської розробки
Додати розробку
