Навчальний посібник "ОСНОВИ СТВОРЕННЯ ІНФОРМАЦІЙНИХ МОДЕЛЕЙ"
|
Комунальний заклад загальної середньої освіти І-ІІІ ступенів №12 Жовтоводської міської ради
|
|
|
ОСНОВИ СТВОРЕННЯ ІНФОРМАЦІЙНИХ МОДЕЛЕЙ Навчальний посібник Рудяков Андрій Володимирович
|
|
|
|
|
|
|
|
|
М . Ж О В Т І В О Д И 2 0 1 8 Р І К |
|
Рудяков А.В.
ОСНОВИ СТВОРЕННЯ
ІНФОРМАЦІЙНИХ МОДЕЛЕЙ

Жовті Води – 2018
Рекомендовано до друку рішенням засідання науково-методичної ради комунального закладу загальної середньої освіти І-ІІІ ступенів №12
(протокол № 2 від 27.10.2018 р)
Рецензент – Наконечна Т.В., доцент кафедри обчислювальної математики та математичної кібернетики Дніпровського національного університету ім. О. Гончара, кандидат фізико-математичних наук,.
Рудяков А.В.
Навчальний посібник містить короткий теоретичний матеріал і завдання за тематикою моделювання та покликаний надати допомогу учням середньої школи, починаючи з сьомого класу, розв’язувати завдання, що виникають перед людьми у повсякденному житті, які прийнято називати «компетентністними задачами», з використанням інформаційних моделей, що можуть бути реалізовані засобами сучасного програмного забезпечення для персональних комп’ютерів. Матеріал посібника викладено у відповідності до матеріалів підручників з інформатики, починаючи з сьомого класу, авторського колективу під керівництвом Й. Я. Ривкінда, як таких, з якими працює автор цього посібника та його учні.
Навчальний посібник призначений для учнів і вчителів загальноосвітніх шкіл, що бажають поглибити свої знання та вдосконалити навички з теми «Моделювання. Інформаційні моделі та їх реалізація засобами програмного забезпечення персональних комп’ютерів».
©Рудяков А.В., 2018
ЗМІСТ
ЗАГАЛЬНІ ТЕОРЕТИЧНІ ЗАСАДИ МОДЕЛЮВАННЯ.................................. 5
ЗАВДАННЯ ДЛЯ САМОСТІЙНОГО ОПРАЦЮВАННЯ.............................. 22
ПЕРЕЛІК ВИКОРИСТАНИХ ДЖЕРЕЛ......................................................... 23
ЗАГАЛЬНІ ТЕОРЕТИЧНІ ЗАСАДИ МОДЕЛЮВАННЯ
Ключем до розв’язання компетентнісних задач є вміння учнів створювати різноманітні інформаційні моделі у відповідних предметних галузях. Ці інформаційні моделі можуть бути представлені у будь-який зручний для розуміння учнями спосіб:
- словесно; - графічно;
- структурно;
- математично або ж представляти собою сукупність всіх цих представлень.
Джош Шелдон, відомий в професійних колах розробник програмного забезпечення та лектор у своєму виступі «Обчислювальне мислення в робочій силі та стандартах науки наступного покоління» на конференції американської національної наукової асоціації викладачів (National Science Teachers Association – NSTA) [1] навів ілюстрацію зв’язків, що існують між окремими етапами дослідницької діяльності людей (дивись рисунок 1).
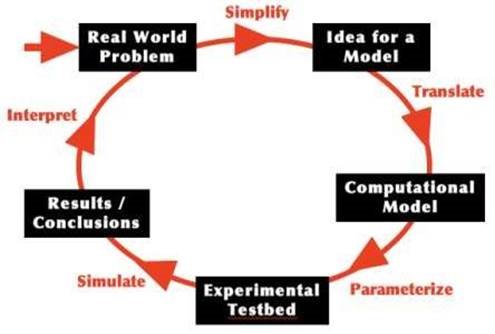
Рисунок 1 Цикл наукових обчислень
В повсякденному житті перед людиною постають певні задачі (Real
World Problem). Після певного спрощення (Simplify) йде добір варіантів моделей, що можна було б використати (Idea for a Model). Ідеї моделей після перетворення – трансляції (translation) використовуються для побудови обчислювальних моделей (Computational Model). Обчислювальна модель доповнюється параметрами (Parameterize), після чого має відбуватись експериментальне тестування отриманої моделі на визначених тестових наборах, які б задовольняли відповідним параметрам (Experimental Testbed). Процес симуляції (Simulate) передбачає створення діючої системи на основі обраної та протестованої моделі, про яку обов’язково робляться висновки (Results/Conclusions). За необхідності ці висновки або результати моделювання інтерпретуються (Interpret) та цикл дослідження проблеми починається з початку, але з урахуванням вже отриманих результатів. Наведена діаграма наочно демонструє, що без моделювання люди не зможуть досліджувати навколишній світ.
У відповідності до [2] всі моделі можна класифікувати так, як зазначено на рисунку 2.
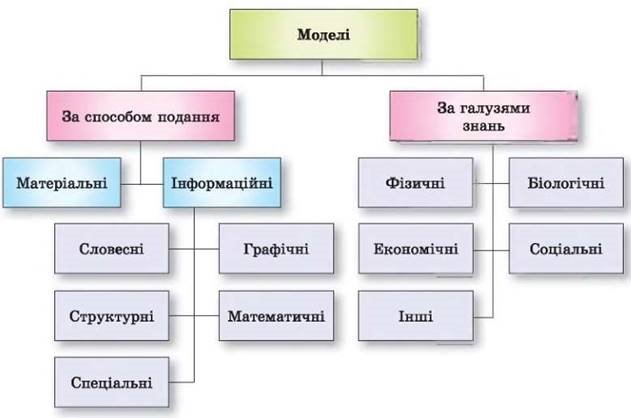
Рисунок 2 Класифікація моделей
Згідно наведеної класифікації розглядатимуться моделі за способом подання – всі з категорії «інформаційних», за галузями знань – здебільшого економічні, оскільки ще однією метою автора є навчання учнів основам фінансової грамотності через використання нескладних для розуміння дітей економічних арифметичних розрахунків, що легко реалізувати засобами, які вивчаються в курсі шкільної інформатики.
Побудова інформаційної моделі виконується за таким алгоритмом
(рисунок 3) [2]:
1. Визначити мету створення моделі.
2. Визначити предметну область дослідження, для якого створюється модель.
3. Виділити ті властивості об’єкта, які є суттєвими для дослідження.
4. Установити взаємозв’язки між значеннями вибраних властивостей, між даним об’єктом та іншими об’єктами предметної області, що є суттєвими для дослідження.
5. Вибрати форму подання інформаційної моделі.
6. Вибрати засіб, з використанням якого буде подано модель.
7. Зобразити модель відповідно до вибраної форми подання, відобразивши в ній суттєві властивості та встановлені взаємозв’язки.
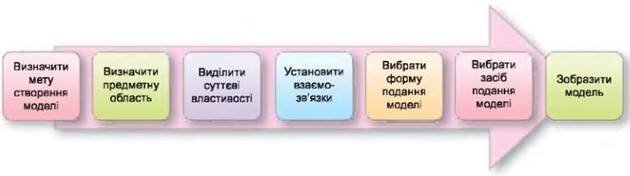
Рисунок 3 Алгоритм побудови інформаційної моделі
Надалі приклади створення моделей розглядатимуться у вигляді уявних практичних задач, що можуть поставати перед підлітками, та з якими учні за наявності прагнення і розуміння завдання можуть впоратись. Щоб не перевантажувати умови завдань деталями, автор подає довизначення окремих умов завдання уже під час його розв’язання. Це робиться навмисне, щоб дати змогу учням самим розуміти процес «довизначення умов» компетентнісних задач за рахунок використання відкритих джерел інформації, зокрема ресурсів мережі Інтернет, що також сприяє розвитку навичок учнів виконувати пошук необхідної інформації за допомогою сучасних засобів інформаційних технологій.
В якості засобів для створення моделей учням пропонуються текстовий процесор на кшталт Microsoft Word 2007 (чи будь-який аналог), редактор електронних таблиць Microsoft Excel 2007 (або аналогічне програмне забезпечення), графічний редактор, що надає базові можливості зі створення та редагування комп’ютерних зображень (типу Microsoft Paint). Такий вибір не є випадковим – за сучасною програмою курсу шкільної інформатики учні загальної школи з сьомого класу повинні володіти базовими знаннями та навичками з використання зазначених програмних засобів і вчителю не доведеться окремо навчати учнів використанню цих програм, хоча вдосконалення навичок учнів з використання такого програмного забезпечення обов’язково матиме місце.
Також посібник містить інші завдання, що можуть бути запропоновані учням для самостійного розв’язання за наведеною в посібнику методикою.
ЗАВДАННЯ 1
Оксана хоче зробити в своїй кімнаті невеликий ремонт шляхом оклеювання стін новими шпалерами. Тато й мама, зайняті на роботі, доручили донці проявити самостійність та розрахувати орієнтовну вартість витратних матеріалів для подальшого планування сімейного бюджету. Оксана мусить провести певну роботу, щоб аргументовано спілкуватись з батьками з приводу запланованого ремонту. Допоможіть Оксані у розв’язанні її проблеми, вартість роботи з оклеювання не повинна враховуватись, оскільки щаслива сім’я – тато, мама і Оксана самі наклеять шпалери.
РОЗВ’ЯЗАННЯ 1
Розв’язання слід виконувати у відповідності до наведеного у п.1 алгоритму.
1. Мета створення моделі та предметна область дослідження, для якого створюється модель, зазвичай, як в цій задачі, частково окреслені в умовах. Тобто метою створення дійсної моделі є виконання завдання з визначення матеріальних (фінансових) витрат на переклеювання шпалер в окремо взятій кімнаті.
2. Предметна область охоплює побутовий ремонт та фінансові витрати (витрачання грошових коштів сім’ї на придбання матеріалів, необхідних для ремонту).
3. Суттєвими властивостями є геометрична форма кімнати (зазвичай у вигляді паралелепіпеда), наявність та кількість дверей, вікон, їх габаритні (найбільші розміри), геометрична форма шпалер – рулон представляє собою зазвичай прямокутник стандартних для виробництва розмірів – 0,5 м × 5 м або 1 м × 5 м, клей, необхідний для наклеювання шпалер на стіни, має властивість витрат на одиницю оклеюваної площі (кв. м). Крім того всі витратні матеріали – шпалери та клей – мають однакову суттєву властивість – вартість.
4. На основі визначених властивостей слід відзначити, що головним зв’язком між ними виступає площа поверхонь: стіни, на які слід наклеювати шпалери, мають певну площу, яку можна визначити, скориставшись математичними обчисленнями. Кожен рулон шпалер також має свою площу, яку він здатен покрити. Шпалерами, відповідно, не покривають підлогу, вікна та двері, а стелю покривають за вибором. Витрати клею можна буде визначити виходячи з площі оклеюваної поверхні. Також суттєвою особливістю даної моделі буде те, що під час розрахунку кількості необхідних рулонів шпалер та упаковок клею треба використовувати ділення з округленням у більшу сторону для отримання цілого числа, оскільки торгівельні організації продають шпалери та клей у відповідних одиницях, що не діляться на більш дрібні.
5. Для створення моделі кімнати більш за все підійде графічна форма представлення, для якої необхідно зазначити всі потрібні розміри. Також для того, щоб отримати відповіді на всі запитання задачі, зручно буде використати табличний спосіб представлення моделі.
6. Виходячи з вибору представлення моделі засобами мають стати – графічний редактор (наприклад Microsoft Paint), або відповідні засоби текстового процесора Microsoft Word 2007, а також редактор електронних таблиць Microsoft Excel 2007.
7. Під час відтворення графічної моделі потрібно зобразити кімнату за таким описом: кімната – прямокутна, габаритні розміри – А метрів на В метрів, висота стелі – С метрів, є (наприклад) 2 вікна розмірами D м на E м та (наприклад) 2 дверей розмірами F м на J м (учні можуть описати власну кімнату). При цьому учні можуть використовувати як готові зображення, знайдені в Інтернеті, як, наприклад, на рисунку 4 (до цього плану потрібно довизначити розміри вікон, дверей, висоту кімнати), так і створені вручну на основі паперових ескізів (рисунок 5). Учні мають визначитись із шпалерами, скориставшись, наприклад, пошуком на маркетплейсі prom.ua за ключовим словом «обои» (шпалери російською), де за результатами пошуку вони уточнять характеристики та вартість шпалер (рисунки 6 та 7).
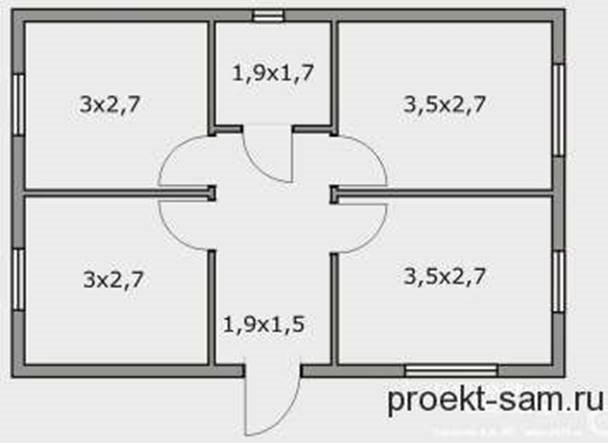
Рисунок 4 План одноповерхового будинку
Для зручного представлення обраної та створеної графічної моделі слід скористатись редактором електронних таблиць та створити в ньому відповідні таблиці, що міститимуть всі визначені величини, необхідні для проведення розрахунків. Приклад такої реалізації наведено на рисунку 8 (файл з електронною таблицею та відповідними даними, що можна використовувати в якості зразка наведено в електронному додатку до посібника). Зручність використання редактора електронних таблиць як то Microsoft Excel 2007 полягає ще й в тому, що він дозволяє виконати всі необхідні математичні розрахунки, що є реалізацією суттєвих зв'язків між властивостями моделі. Площа стін приміщення є сумою площ стін
(1):
𝑆стін = 2 × 𝐴 × 𝐶 + 2 × 𝐵 × 𝐶 (м кв. ), (1)
де А – довжина кімнати в метрах,
В – ширина кімнати в метрах, С – висота кімнати в метрах.
За потреби до цієї площі можна додати площу стелі, що дорівнює (2):
𝑆стелі = А × В (м кв. ) (2)
Ці формули на аркуші Excel, що показаний на рисунку 7, містяться у комірках В5 та В6 відповідно. Очевидним є те, що вікна та двері шпалерами не заклеюються, тобто площі відповідної кількості вікон та дверей у кімнаті вираховуються з загальної площі поверхонь кімнати.
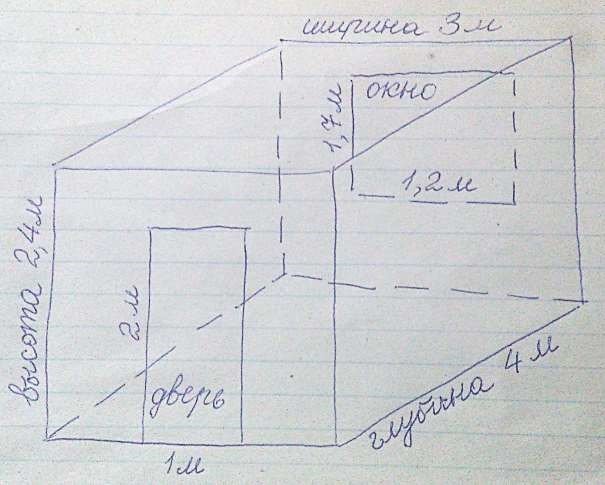
Рисунок 5 Паперовий ескіз – основа графічної моделі
Коли стала відомою площа, яку необхідно покрити шпалерами, слід з’ясувати, скільки для цього необхідно рулонів шпалер та упаковок клею для шпалер. Для визначення кількості рулонів шпалер слід отриману за формулою (1) площу розділити на площу одного рулону шпалер, а результат ділення округлити в більший бік до цілого.
Формула для комірки В15 на рисунку 8 має вигляд:
=ОКРУГЛВВЕРХ(B7/B14;0)
Рисунок 6 Приклад пошуку
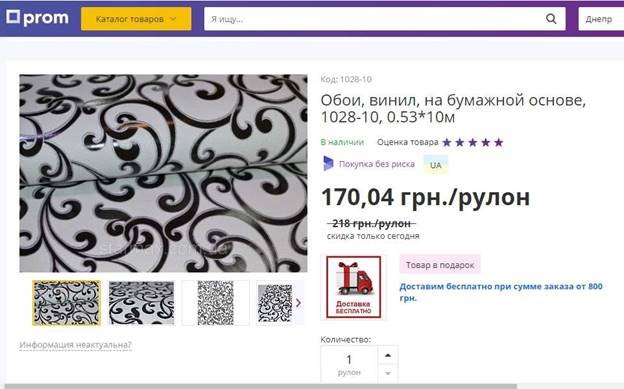
Рисунок 7 Один з результатів пошуку шпалер на prom.ua Для визначення кількості клею слід площу (1) розділити на число, що береться з характеристик клею як «витрати на площу». Ці витрати виробники зазначають як діапазон чисел, наприклад – «упаковка призначена для покриття площі від 30 до 40 м кв.» – слід брати для розрахунків менше число з діапазону.
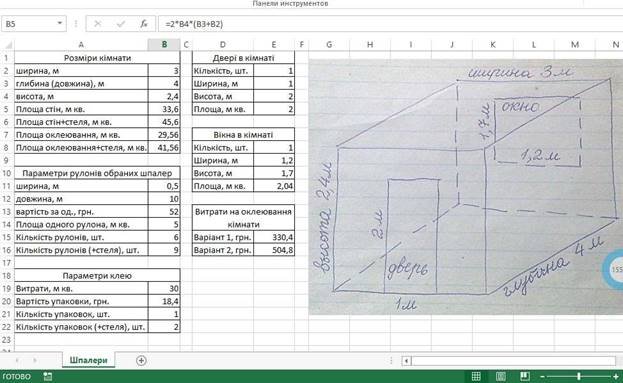
Рисунок 8 Реалізація табличної моделі в Microsoft Excel 2007 Для остаточних розрахунків слід вартість одиниці вимірювання матеріалів помножити на їх отриману кількість та просумувати отримані величини. Під варіантом 1 на рисунку 8 розуміється оклеювання шпалерами кімнати без оклеювання стелі, варіант 2 – зі стелею.
Подальшим розвитком цієї задачі може стати комбінування різних шпалер для оклеювання стін та стелі, що може урізноманітнити варіанти створюваних учнями моделей.
ЗАВДАННЯ 2
Оксана хоче оновити свою кімнату шляхом фарбування стін спеціальною фарбою та оздобленням стелі багетами під гіпсову ліпнину. Допоможіть Олені впоратись з розрахунками орієнтовних фінансових витрат на придбання відповідних матеріалів.
РОЗВ’ЯЗАННЯ 2
Для розв’язання цієї задачі слід діяти у відповідності до алгоритму, згідно з яким було розв’язане завдання 1 з тією різницею, що важливою властивістю одного з об’єктів, що присутній в моделі, а саме фарби, є зв’язок з об’ємом фарби та площею поверхні, що може покрити ця фарба. Як і в попередньому прикладі з клеєм для шпалер слід брати до розрахунків число, вказане в характеристиках дібраної для розв’язання прикладу фарби, що відповідає більшим витратам, тобто наприклад, якщо в характеристиках фарби зазначено «витрати: 100-200 г/м кв.», слід брати до розрахунків число 200. Слід пам’ятати, що для отримання вірного результату необхідно всі величини в розрахунках привести до одних одиниць вимірювання, наприклад, всі характеристики матеріалів перевести з грамів у кг, а з сантиметрів – в метри.
Також при побудові графічної та табличної моделі для розв’язання задачі слід пам’ятати, що багети мають клеїтись по периметру стелі, тобто їх загальна довжина має дорівнювати периметру кімнати (не менше). Багети можуть клеїтись в стик, крім того, для їх монтажу також потрібен клей, кількість якого також необхідно обрахувати.
Приклад розв’язання задачі з відповідними графічною та табличною моделлю наведено на рисунку 9 (файл з формулами та розрахунками – в електронному додатку до посібника).
Під час розглядання цієї моделі учні знайомляться з особливостями мулярських технологій на початковому рівні, що дає змогу показати, який це насправді непростий процес та які конкретно питання постають перед професіоналами у цій сфері. Крім того учні вчаться критичного мислення щодо витрат коштів сім’ї на подібні потреби.
Зазвичай фарба для внутрішніх приміщень виготовляється білого кольору, тож якщо учні хочуть отримати для Оксани кольорову кімнату, їм знадобиться врахувати у загальні витрати відповідну кількість так званого пігменту – речовини, що робить білу фарбу кольоровою. Тут слід зазначити, що співвідношення ваги пігменту до ваги фарби не повинно перевищувати 10:100 – за такого співвідношення отримується дуже насичений колір.
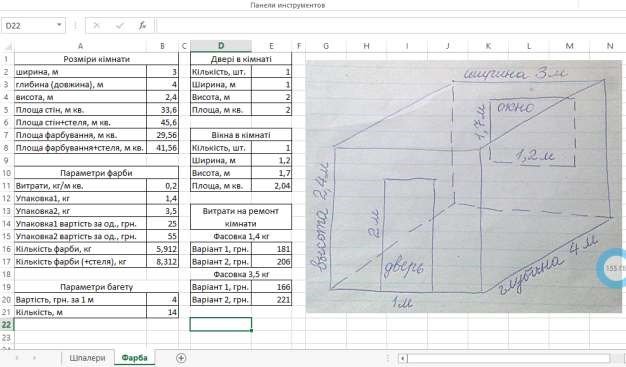
Рисунок 9 Приклад реалізації моделі в Microsoft Excel 2007
Наведена на рисунку 9 модель не враховує вартості витрат на колорування фарби, тому це пропонується зробити учням самостійно.
Також дуже цікавими і показовими є результати розрахунків: за умови використання меншої фасовки фарби вартість матеріалів для варіанта без стелі більша, ніж у випадку використання більшої фасовки – 3,5 кг. І навпаки, для фасовки 1,4 кг вартість варіанта зі стелею менша, ніж для фасовки 3,5 кг. Це пов’язано з тим, як число, що позначає вагу фасовки співвідноситься з числом, що являє собою витрати фарби на відповідну площу. Цей приклад може служити основою для пояснення учням такого розуміння, як «оптимізація витрат».
Подальшим розвитком цієї задачі може бути використання різнотипних фарб для оздоблення інтер’єра кімнати Оксани, що потребуватиме від учнів внесення відповідних коректив в модель. Можна для більшої наочності запропонувати учням створити графічну модель засобами будь-якого доступного графічного редактора, в якому відповідні частини необхідно розфарбувати, як, наприклад, на рисунку 10. Тобто, враховуючи, що кімната, зазвичай представляє собою по формі паралелепіпед, можна запропонувати учням створити кольорову розгортку паралелепіпеда, що також сприятиме розвитку їх просторової уяви.
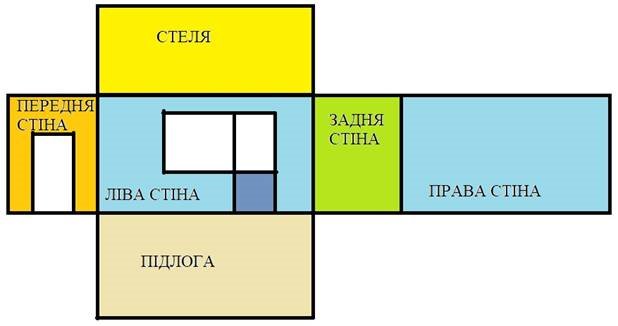
Рисунок 10 Приклад графічної моделі кімнати у вигляді розгортки
Продовженням такого моделювання може стати виготовлення паперової моделі кімнати.
ЗАВДАННЯ 3
Читаючи оповідання про піратів, Арсеній звернув увагу а те, що іноді відчайдухи витягали коштовності з кораблів через корабельні ілюмінатори, що зазвичай мають форму кола. Питання, яке виникло у Арсенія, чи могли пірати витягати через ілюмінатори сундуки чи ящики прямокутної форми?
РОЗВ’ЯЗАННЯ 3
Для розв’язання цієї задачі слід діяти у відповідності до алгоритму, згідно з яким було розв’язане завдання 1. Важливими властивостями об’єктів, що присутні в задачі, є внутрішній діаметр кола корабельного ілюмінатора та діагональ прямокутника бічної поверхні ящика чи сундука. Зв’язок між цими властивостями видно з рисунку 11, на якому d – це діаметр кола ілюмінатора, a, b, c – сторони паралелепіпеда, яким є сундук або ящик, d1, d2, d3 – діагоналі прямокутників, що утворюють паралелепіпед.
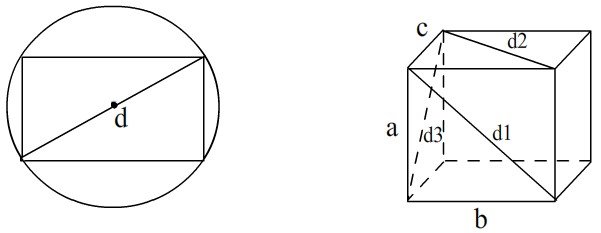
Рисунок 11 Графічна модель для розв’язання задачі
На основі графічної моделі нескладно реалізувати математичну модель, яка в основі використовує теорему Піфагора (3), (4), (5):
𝑑![]() (3)
(3)
𝑑![]() (4)
(4)
𝑑![]() (5)
(5)
Після виконання розрахунків необхідно діаметр кола ілюмінатора d порівняти з усіма діагоналями паралелепіпедів d1, d2 та d3. За умови, якщо хоча б одна з діагоналей буде меншою за діаметр, піратам вдасться витягти цей ящик через ілюмінатор (якщо піднімуть☺).
Алгоритм розв’язання цього завдання наведено на рисунку 12.
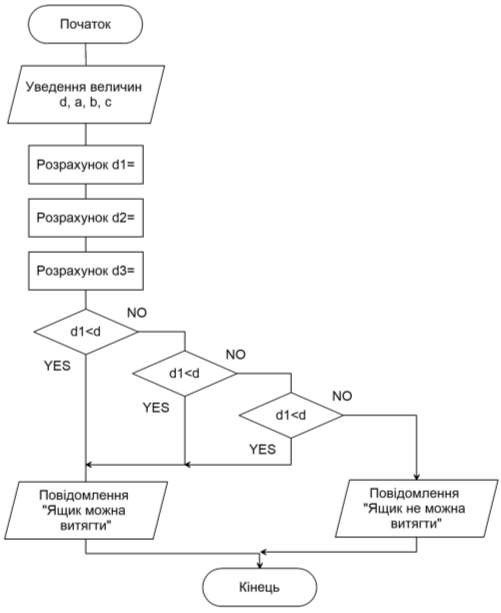
Рисунок 12 Алгоритм розв’язання поставленого завдання
Для учнів 8-го та старших класів, що вже вивчали тему «Основи подійного та об’єктно-орієнтованого програмування» і знайомі з мовою програмування ObjectPascal та середовищем програмування Lazarus може бути запропоновано реалізувати цей алгоритм засобами мови програмування
ObjectPascal. Нижче наведено лістинг програми мовою Pascal, що реалізує поставлене завдання, в цьому лістингу виділено фрагменти програмного коду, що можуть бути пропущені для того, щоб учні могли вставити вірні строчки для вірної реалізації програми:
uses crt; var d, a, b, c, dl, d2, d3:real;
begin clrscr; read(d, a, b, c); dl:=sqrt(sqr(a)+sqr(b)); d2:=sqrt(sqr(b)+sqr(c)); d3 :=sqrt(sqr(a)+sqr(c)); if (d>=d 1 )or(d>=d2)or(d>=d3) then write('Ящик вытащить возможно') else write ('Ящик вытащить невозможно'); readkey;
end.
Дизайн екранної форми (розміри, наявність на ній полів для введення та кнопок управління) учні мають розробити самостійно, а також адаптувати код з мови Pascal на ObjectPascal.
ЗАВДАННЯ ДЛЯ САМОСТІЙНОГО ОПРАЦЮВАННЯ
ЗАВДАННЯ 4
Петрик з татом хочуть збудувати вбудовану у комору шафу для збереження хатніх речей та інструментів. Для цього їм потрібно придбати відповідну кількість матеріалу – ламінованої деревоволокнистої плити (ЛДВП). Допоможіть Петрику визначити фінансові витрати виходячи з того, що торгівельна організація постачає ЛДВП у вигляді нарізаних шматків розміром 2х1 м.
ЗАВДАННЯ 5
Оленка просить тата побудувати їй на подвір’ї їхнього будинку «ляльковий будиночок». Тато доручив старшій сестрі Оленки – Оксані, що навчається у восьмому класі, скласти кошторис витрат на купівлю витратного матеріалу – дерев’яної струганої дошки та акрилової фарби. Допоможіть Оксані виконати доручення тата та допомогти молодшій сестрі Оленці отримати омріяний «ляльковий будиночок».
ЗАВДАННЯ 6
Дмитро почув від друзів, що за умови використання енергозаощаджуючих ламп на основі світлодіодів можна суттєво скоротити витрати не електроенергію для сім’ї, що дасть змогу на зекономлені кошти оновити хлопцю телефон. Допоможіть Дмитру з’ясувати, чи дійсно таким чином можна зберегти сімейний бюджет та спрямувати вивільнені кошти на інші потреби?
ПЕРЕЛІК ВИКОРИСТАНИХ ДЖЕРЕЛ
1. Josh Sheldon. Computational Thinking in the Workforce and Next Generation Science Standards at NSTA 2014 (April 4)
https://www.slideshare.net/joshsheldon/computational-thinking-in-theworkforce-and-next-generation-science-standards-at-nsta-2014-april-4 // Sheldon Josh, Conference of National Science Teachers Association, 04 april 2014.
2. Ривкінд Й. Я., Лисенко Т. І., Чернікова Л. А., Шакотько В. В. Інформатика : підруч. для 8-го кл. загальноосвіт. навч. закл. / Й. Я.
Ривкінд [та ін.]. — Київ : Генеза, 2016. — 288 с. : іл.
3. Ривкінд Й. Я., Лисенко Т. І., Чернікова Л. А., Шакотько В. В. Інформатика : підруч. для 9-го кл. загальноосвіт. навч. закл. / Й. Я.
Ривкінд [та ін.]. — Київ : Генеза, 2017. — 288 с. : іл.
4. Ривкінд Й. Я., Лисенко Т. І., Чернікова Л. А., Шакотько В. В. Інформатика : підруч. для 10-го кл. загальноосвіт. навч. закл. (рівень стандарту) / Й. Я. Ривкінд [та ін.]. — Київ : Генеза, 2010. — 296 с. : іл.
5. Ривкінд Й. Я., Лисенко Т. І., Чернікова Л. А., Шакотько В. В. Інформатика : підруч. для 11-го кл. загальноосвіт. навч. закл. (рівень стандарту) / Й. Я. Ривкінд [та ін.]. — Київ : Генеза, 2011. — 304 с. : іл.


про публікацію авторської розробки
Додати розробку

