Проект " Математика - справді цікаво"

Дослідницько-пошуковий міжпредметний проект

4-й клас

 Мета проекту: Поглибити та розширити знання учнів про головоломки, задачі з логічним навантаженням та способи їх розв’язання ; повправляти у виконанні таких завдань. Ознайомити з іменами деяких відомих математиків. Формувати вміння працювати з різноманітною літературою, інтернетом. Розвивати пізнавальні інтереси, логічне, творче мислення. Виховувати відповідальність за результати власної колективної діяльності, інтерес до вивчення математики.

   Тип проекту:   груповий, довготривалий.

     Обладнання: фотографії, ілюстрації, схеми, портрети математиків,   пізнавальна література, задачі, сірники.

 Консультанти:  класовод ( керівник проекту ), бібліотекар, вчитель інформатики, батьки.                              

        Підготовчий етап

1. Визначення та обговорення з учнями теми та завдань проекту.

2. Пошук і аналіз проблеми.

Під час обговорення теми виникли запитання:

       • Звідки прийшли до нас головоломки?

       • Як класифікувати задачі з логічним навантаженням?

       • Як розв’язувати подібні завдання?

       • Який внесок відомих математиків у розвиток науки?

       • Чи справді математика – це цікаво?

3. Постановка мети проекту.

4. Визначення критеріїв оцінки проекту.

1. Завершеність.
2. Ясність, грамотність, чіткість.
3. Інформація (правдивість, важливість, використання різних джерел).
4. Графічне оформлення (наявність фотоматеріалів, схем, малюнків).
5. Вміння працювати в групі.

5. Створення дослідницьких груп: «Історики»,  «Логісти»,  «Стратеги», «Інформатики».

Основний період

1. Аналіз наявної інформації.

2. Збір даних з використанням різних джерел інформації.

3. Проведення спостережень та експериментів.

4. Отримання консультацій.

5. Проведення циклу класних та інформаційних годин.

6. Організація конкурсу малюнків та схем.

7. Систематизація та оформлення зібраних матеріалів.

8. Створення газети.

9. Підготовка та проведення творчого звіту груп.

Презентація проекту

   •  Презентація творчих надбань.

   •  Ознайомлення з виставкою матеріалів, над якими варто   «поломати» голови.

   •  Урок-подорож до країни «Акитаметам»

        Завдання  групи:

• вивчити та доповісти історію виникнення головоломок;
• запропонувати власну класифікацію цікавих математичтих завдань;
• дізнатися як «ломали голови» над математичними завданнями відомі математики.                                                              

                        З історії головоломок

        Головоломок існувало і існує так багато, що для опису короткої     історії і принципу кожної з них знадобилася б велика книга. Вони існують дуже різні – дерев’яні, пластмасові, мотузкові, плоскі та об’ємні. Об’єднує всі головоломки одне – поставлене завдання досить важко розв’язати, потрібно «поломати» голову.

        Головоломки існують дуже давно. Вже 4000 років назад в Китаї була відома гра «Танграм». Відомі головоломки, придумані стародавніми греками Піфагором і Архімедом. Але існує дві головоломки, які зацікавили весь світ: кубик Рубіка і гра «П’ятнашки».

        Гра «П’ятнашки» відноситься до типу переставних головоломок. В прямокутній коробочці, заповненій квадратними фішками, є пусте місце, яке дозволяє пересувати фішки, не виймаючи їх з коробочки. Фішки переплутуються і гравець, шляхом послідовних рухів, повинен розставити фішки в правильному порядку.

       Крім цієї гри є ще багато цікавих ігор для одного гравця, пов’язаних з переміщенням фішок і елементів. Н-д: « Останній воїн», « Кольорова мозаїка» та ін.

       Відома в усьому світі стародавня китайська гра-головоломка «Танграм» виникла 4 тисячі років назад. Суть її полягає в складанні з семи частин, отриманих розрізанням квадрата визначеним способом, різних фігур. Правила цієї гри досить прості. До складу кожної фігури мають входити усі сім частин, при цьому вони не повинні перекриватися.

       «Кубик Сома» - трьохмірний аналог гри «Танграм». Його придумав датчанин Піт Хейн під час лекції по квантовій механіці. В голову Хейна прийшла цікава думка, що якщо взяти всі неправильні фігури, складені з трьох або чотирьох кубиків, склеяних між собою гранями, то з них можна скласти один куб великого розміру.

         Світ влаштований так, що речі в ньому можуть жити довше, ніж люди, мати різні назви в різних країнах. Але на протязі століть залишатися улюбленими для багатьох поколінь. Саме так відбувається з головоломками. В середні віки моряки і купці. Воїни і дипломати збавлялись головоломками і заодно розвозили їх по світу. Сьогодні в них грають дорослі і діти на різних континентах.

                           Кубик з хрустом

        Рекорди популярності побив відомий « Кубик Рубика»,винайдений в 1974 році венгром Ерне Рубиком. Пластмасовий куб з 26 малих кубиків, які обертаються навколо невидимої осі, потрібно розставити, щоб кожна грань складалася з одноколірних квадратів. Число станів куба рівняється 43 252 003 274 489 856 000, при цьому іграшку можна зібрати всього за 29 ходів.

        В середину куба помістили циліндричний механізм, який скріплює кубики, але дозволяє їм обертатися. Побічним ефектом компромісу між щільністю з’єднання і свободою обертання ста характерний хруст.

       Кубик Рубика став лідером по кількості продаж: по всьому світу продали 300 млн. штук. В 1982 р. в Будапешті пройшла перша світова першість по складанню. А в Кноксвілі кубику навіть поставили пам’ятник.

            200 років тому в Німеччині жив і творив математику    видатний вчений Гаусс.

             Ще в школі проявився його талант до математики. Одного разу його вчитель, маючи потребу залишити на уроці дітей самих у класі на довший час, запропонував учням записати суму усіх чисел від 1 до 100 і обчислити її. Відповідь сам знайшов заздалегідь. Учитель пішов, але незабаром повернувся, бо забув якусь річ. У цей час малий Гаусс вигукнув: « Я вже обчислив!» Вчитель розсердився, не повірив. А юний математик дійсно отримав результат, який співпадав із відповіддю вчителя, виконавши обчислення зручним способом. 1+2+3+4+5…+96+97+98+99+100=(1+100)+(2+99)+…=.

            Гаусс підмітив, що суми, складені з першого і останнього числа ряду, другого і передостаннього і т. д. рівні між собою. Скільки вони дорівнюють? (101.) Скільки таких пар буде вцьому ряду? Якщо всього доданків 100, то пар буде 50. От Гаусс і помножив101 на 50 і одержав(5050)

              Дослідивши цікаві математичні задачі та головоломки ми прийшли до наступної класифікації:

          Задачі:

• на припущення;
• на вилучення;
• на встановлення закономірності;
• на математичні обчислення.

        Головоломки:

• дерев’яні, пластмасові, паперові;
• плоскі, об’ємні;
• шнуркові, переставні.

Завдання нашої групи:

• підібрати задачі, що містять стратегічні ситуації;
• пояснити способи їх розв’язання;

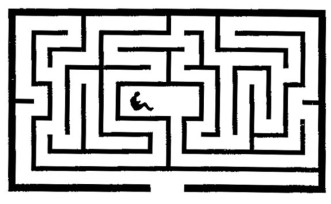
Як вийти із справжнього лабіринту

      Якщо довелось шукати виходу лабіринту на плані, то вихід обов’язково знайдеться,тут дозволено навіть зайвий раз помилитися. Зовсім інша справа – знайти дорогу, якщо ви маєте охоти до нестями блукати в переходах лабіринту й не знаєте плану його.

      Треба вигадати якогось систематичного способу, Чи, може, ви гадаєте, що бувають «безвихідні лабіринти», тобто такі, що до них можна зайти, але не можна потім знайти виходу? Подумайте з приводу цього.

      Уявіть собі, що вас, наприклад, посажено в центрі ла біринту, зображеного на малюнку.

Плану у вас немає. Навколо темрява. Та невже ви нічого не вигадаєте задля порятунку свого життя? Спробуйте!

Пояснення

      Звичайно, перше, що слід випробувати в такому випадку – це просто йти вздовж стінки, весь час торкаючись її лівою (або правою) рукою .Цей шлях виведе вас на волю, правда, не найкоротшим шляхом.

      Але, якщо центр лабіринту охоплено стінкою в формі розірваного кола або складнішої форми, але такої, що стінка не доходить безперервно до зовнішніх стін, то правило не годиться.

    Французький математик Тарі винайшов правило, що може завжди допомогти вийти лабіринту.

      Ідучи якимось проходом, ви мусите зазначати на стінці пройдений вами шлях. Це треба робити при вході на роздоріжжя й при вході на новий прохід. На кожному роздоріжжі ви можете вибрати дальший шлях навмання, але, попадаючи вперше на роздоріжжя певним шляхом, ви мусите при дальших поворотах знову до цього роздоріжжя уникати першого шляху доти, доки це можливо. Лише в разі , якщо ви вже пройдете всі інші шляхи з цього роздоріжжя двічі, ви мусите піти знову шлях ом, що ви ним уперше прийшли на це роздоріжжя.

     Додержуючись цього правила, ви неодмінно знайдете вихід із лабіринту (або його центр, якщо ви почали зовні), пройшовши не більше, як двічі, всі коридори.

     Але треба визнати, що в темряві це зовсім не так легко зробити…

     І пробачте, будь ласка, що раз-у-раз до темних льохів заходите. Незабаром ми вийдемо з вами на широкий світ і пошукаємо пригод та завдань в приємніших умовах.

   Чому б не спробувати перевірити свої здібності перемістившись у стайню?

Переміщення в стайні

Верблюди та коні

       В стайні, що має дев’ять окремих стійл, стоять чотири верблюди (В) та чотириконі (К), а одне стійло (середнє) вільне.

 Треба перевести всіх коней на місце верблюдів та навпаки, додержуючись таких умов:

1. Не можна одночасно переводити двох тварин.
2. В кожному стійлі одночасно може перебувати лише одна тварина.
3. Верблюда можна переводити щоразу лише до правішого стійла або через одне.
4. Коня можна переводити або до сусіднього стійла зліва, або через одне ліворуч.

Як можна зробити таке переміщення?

Пояснення

     Це завдання вигадав талановитий французький математик Едуард Люка; розв’язати його дуже легко.

      Розгляньте лише уважно всі можливості. Спочатку можна переводити коня або верблюда; це, очевидно, значення не має, бо їхнє розташування цілком однакове. Але як верблюдами, так і кіньми можна перше кожне переміщення зробити подвійно: «стрибок» або «простий хід».

       Якщо ви спершу стрибнете, наприклад, верблюдом, то потім вам знову обов’язково доведеться переводити верблюда і далі знову так само, аж поки вільне місце перейде зовсім до лівого боку, а тоді… взагалі ви нічого не зможете переміщувати ( бо верблюдів ви не маєте права зрушити ліворуч ). Отже стрибок на початку – помилка!

       Треба просто посунути верблюда( можна було б почати й з

коня) на одне стійло праворуч. Тоді через нього зможе «стрибнути» ближчий кінь. Розбираючися таким чином у дальших переміщеннях, ви легко знайдете все розв’язання.

       Слідкуйте за схемою, рядки показують становище після кожного переміщення; вільне стійло - □.

Спритні свідки

      Без зайвих слів детектив виклав свою проблему: « Ми маємо п’ятьох свідків, яким не довіряємо. Маємо також десятьох підозрюваних у торгівлі наркотиками. Щодо кожного підозрюваного свідки дали свідчення про наявність у того наркотиків.»

  Ось усі їхні свідчення:

 Підозрюваний 1: Усі п’ятеро свідчать, що підозрюваний має         наркотики.

 Підозрюваний 2: Усі п’ятеро свідчать, що він не має наркотиків.

 Підозрюваний 3: Троє свідчать, що підозрюваний не має наркотиків, двоє – що має.

 Підозрюваний 4: Усі п’ятеро свідчать, що підозрюваний має наркотики.

 Підозрюваний 5: Четверо свідчать, що підозрюваний має наркотики, один – що не має.

 Підозрюваний 6:  Усі п’ятеро свідчать, що підозрюваний не має наркотиків.

 Підозрюваний 7:  Троє свідчать, що підозрюваний має наркотики, двоє – що не має.

 Підозрюваний 8:  Усі п’ятеро свідчать, що підозрюваний має наркотики.

 Підозрюваний 9:  Усі п’ятеро свідчать, підозрюваний не має наркотиків.

 Підозрюваний 10: Четверо свідчать, що підозрюваний не має наркотиків, один – що має.

       Чи можете ви сказати, хто з підозрюваних має наркотики, за умови, що свідки збрехали точно дев’ять разів, а неправдивим було переважно твердження «не має наркотиків», тоді як правдою є «має наркотики». Вони – «підкуплене стадо».

Задля розминки:Яку найменшу кількість разів могли б збрехати   свідки?

Розв’язок розминки: Кожне не одноголосне свідчення (розходження) повинно узгоджуватися з кількістю випадків фальші, тобто повинне бути адекватним до меншості або, можливо, більшості свідчень. Як бачимо, є чотири випадки розходження: двічі – три проти двох і двічі – чотири проти одного.

  Додавання менших свідчень дає нам шість випадків брехні.

Відповідь до головоломки:

          З дев’яти фальшивих свідчень, що їх дали спритні свідки,повинно бути принаймні п’ять фальшивих тверджень невинуватості («підозрюваний не має наркотиків»). Тільки один сценарій дасть такий результат – якщо підозрювані 1, 4, 5, 7, 8 і 10 – мають наркотики, а решта – ні.

Учасники нашої групи пропонують повправлятись у розв’язанні логічних задач.             

Логічні задачі

1. У дівчинки стільки ж братів, скільки й сестер, а в хлопчика з цієї сім’ї братів немає. Скільки в цій сім’ї хлопчиків і скільки дівчаток?

2. У батьків було три дочки, у кожної з них було по два брати. Скільки всього дітей у цій сім’ї?

3. Двоє батьків, двоє синів та дідусь з онуком піймали по 6 окунів, а всього 18. Як це могло статися?

4. Троє хлопчиків – Мишко, Сергійко, та Сашко живуть в одному під’їзді на різних поверхах: п’ятому, сьомому та восьмому. Михайлик живе не нижче за Сашка, а Сергійко – не вище за Сашка. Хто з хлопчиків на якому поверсі живе?

5. Назвіть п’ять днів підряд, не вживаючи чисел та назв днів тижня.

6. З коробки, у якій 7 червоних і 5 синіх олівців, навмання беруть олівці. Яке найменше число олівців треба взяти, щоб серед них було не менш як два червоних і не менш як три синіх?

7. Під час гри вожатий попросив Сергійка вишикувати 12 жовтенят у три ряди так, щоб у кожному було по п’ять жовтенят. Спочатку Сергійко подумав, що виконати це завдання не можна. Проте, зміркувавши, зробив усе як належало. Як він це зробив?

8. Переставте одне число в ряді 20, 17, 14, 5, 11, 8, 2 так, щоб усі числа були розташовані в певному порядку.

9. Сергійко стверджував, що в цьому році буде місяць з п’ятьма неділями та п’ятьма середами. Чи правий він?

надали значну допомогу в оформленні проекту та запропонували усім його учасникам пограти в комп’ютерні ігри, які «тренують розум»

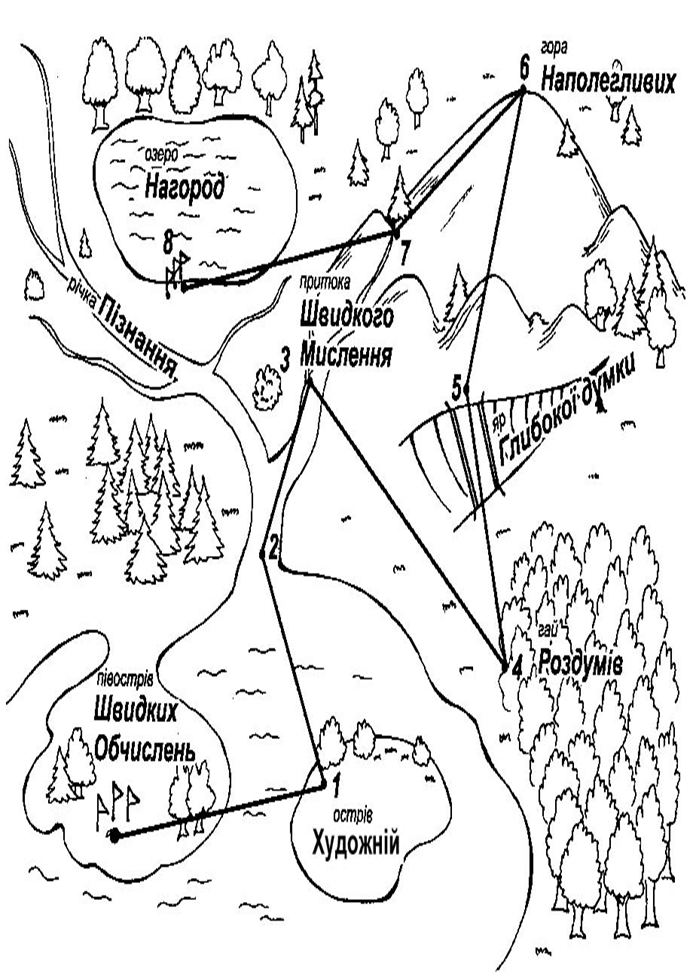
План подорожі

Завдання використані для подорожі

На півострові Швидких обчислень.

1. Групи розфарбовують по одному виду транспорту , а на найшвидшому здійснюється подорож країною «Акитаметам».

На острові Художньому.

   1. Учні по групах розфарбовують Вінні-Пуха, який теж хоче  подорожувати до чарівної країни.

2. Вінні пропонує розв’язати про нього задачі:

1. Коли Вінні-Пух і П’ятачок прийшли в гості до Кролика, Вінні-Пух з’їв 4 банки згущеного молока та 8 банок меду. Кролик і П’ятачок з’їли кожен по чверті того, що з’їв Вінні-Пух. Скільки банок із такою смакотою було Кролика до того, як прийшли гості, якщо після того, як вони пішли, не лишилося нічого?

2. Якщо використовувати залізну миску для супу як плавальний засіб, то вона утримує півкілограма вантажу. Маса Вінні-Пуха дорівнює 2кг. Скільки мисок потрібно Вінні-Пухові, щоб переправитися через струмок? Як ти собі уявляєш цю переправу?

3. Вінні-Пух збирається до країни «Акитаметам». Він склав у рюкзак10 банок згущеного молока масою по півкілограма кожна, 5 глечиків меду по 2кг кожний та 2 банки вишневого варення масою 3кг кожна. Він би узяв ще їжі, та більше йому не донести. Що доведеться Вінні-Пухові викласти, щоб узяти в рюкзак замість їжі П’ятачка, маса якого два з половиною кілограми?

На річці Пізнання учасники проекту знайомляться ще з одним математиком.

1.      Півтори тисячі років тому жив давньогрецький математик Піфагор.

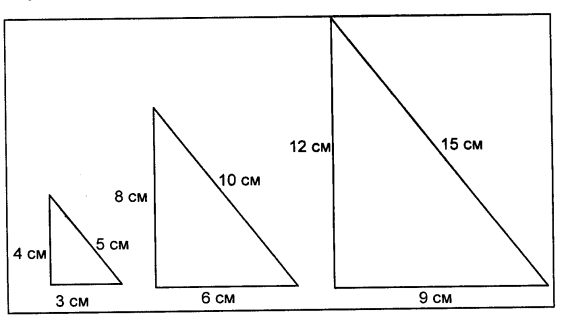
          Щоб стати учнем школи Піфагора, молодий грек повинен був голодувати 40 днів. Піфагор вважав, що числа мають магічні властивості. Його учні шукали трійки «досконалих чисел» - це числа, для яких справджується рівність, наприклад, така: 3∙3+4∙4=5∙5(учні перевіряють цю рівність). Не всяка трійка чисел підходить. Перевірка досконалості чисел 4, 5, 6 і 6, 8, 10.

          Трійки «досконалих» чисел цікаві ще й тим. Що трикутник, у якого довжини сторін дорівнюють цим числам, є прямокутним.

Щоб переправитися через притоку Швидкого Мислення потрібно швидко і логічно мислити.

• Коли у людини буває стільки очей, скільки днів у році?

• Йшла бабця до Львова

назустріч їй три діди,

а в дідів по лантуху,

а в кожному лантусі по коту.

Скільки разом йшло до Львова?

• Коли 2 і 2 бувають більше чотирьох?

• Уявіть, що ви капітан космічного корабля. У вашому розпорядженні команда з шести членів екіпажу. Кожному з них 25 років. Скільки років капітану космічного корабля?

В гаю Роздумів учні мають допомогти хлопчику.

1. На малюнку зображено ліс (із сірників) і хлопчика, що їде до  бабусі. Перекладіть два сірники так, щоб він повертався назад.

У яру Глибокої думки подорожуючі зустрічаються з задачею на припущення.

   До царя Гороха дійшли чутки, що хтось із трьох богатирів убив Змія Горинича. Цар наказав усім трьом богатирям з’явитися до палацу та розповісти, як це сталося.

   Ілля Муромець: «Змія убив Добриня Микитич.»

   Добриня Микитич: «Змія убив Альоша Попович.»

   Альоша Попович: «Я убив Змія.»

Відомо Що один з них сказав правду, а інші збрехали. Хто вбив Змія?

   Піднявшись на вершину гори Наполегливих учні виконують завдання з Кубиком- рубиком ( час визначений ).

Подолавши усі перешкоди, які чекали нас на зупинках ми нарешті дісталися до озера Нагород. На цій зупинці ми оцінимо свою роботу і повернемось додому.

Література

1. Беденко М. В. Математика – це справді цікаво! Збірник задач для учнів початкових класів. – Тернопіль: «Навчальна книга – Богдан», 1999.
2. Вихор Світлана Нестандартні уроки математики 5-6 класи. – Тернопіль: Підручники і посібники, 2005.
3. Гавріна С. Є., Кутявина Н. Л., Топоркова І. Г., Щербина С. В. Логіка – Москва: Ексмо, 2003.
4. Друзь Б. Г. Творчі вправи з математики для початкових класів. Посібник для вчителів. – Київ: Радянська школа, 1988.
5. Енциклопедія для юних джентльменів. – Харків: промінь, 2009.
6. Карнаух П. М. Цікаві завдання з математики. 4 клас. Навчальний посібник. – Тернопіль: Навчальна книга – Богдан, 2007.
7. Корчевська О., Кордуба Н. Нестандартні уроки з математики 1-4 класи. – Тернопіль: Астон, 2003.
8. Клименченко Д. В. Збірник вправ з математики для початкових класів. Методичний посібник – Київ. Радянська школа,1987.
9. Кухар В. М., Барнична Ю. Ю. Цікава математика у 4 і 5 класах. – Київ:Радянська школа – 1975.

10.Митник О. Я. Логіка. Експериментальний навчальний посібник. – Київ: «Початкова школа», 2004.

11.Нікітін Ю. З. 100 затєй для дітей. –Київ: ЦК ЛКСМУ «Молодь» - 1987.

12.Пашкевич Т. М. Контрольні роботи з математики для 3 класу – Київ6 СПД-ФО Тернов І. Є.,2008.

13.Підручна М. В., Янченко Г. М. Позакласна робота з математики у неповній середній школі ( 1 частина). – Тернопіль: Підручники і посібники. 2005.

14.Розумні ігри. – м.:ЗАО «Росмен – прес», 2009.

   15. Інтернет-ресурси