Тема:Рівноприскорений рух, прискорення, одиниці приско-рення. Шлях, переміщення при рівноприскорено-му русі. Графіки швид-кості та прискорення при рівноприскореному русі.

Тема:Рівноприскорений рух, прискорення, одиниці приско-рення. Шлях, переміщення при рівноприскорено-му русі. Графіки швид-кості та прискорення при рівноприскореному русі.

Мета: сформувати знання про рівноприскорений рух і прискорення, швидкість тіла і пройдений шлях під час рівноприскореного прямолінійного руху, графічне зображення модуля переміщення на графіку швидкості в рівноприскореному русі, умінь виводити формулу проекції переміщення; виробляти вміння обчислювати прискорення, знаходити проекцію миттєвої швидкості за проекціями початкової швидкості і прискоренням; формувати відповідні знання і вміння щодо розв'язання основної задачі механіки.

Тип уроку: урок вивчення нового навчального матеріалу.

ХІД УРОКУ 

1. Привіттання з класом,перевірка відсутніх.
2.  Вивчення нового матеріалу

У ході лекції з використанням демонстрацій учні конспектують матеріал.

Рух матеріальної точки, під час якого її швидкість за будь-які однакові проміжки часу збільшується або зменшується на ту саму величину, називається рівнозмінним. Такий рух є найпростішим нерівномірним рухом. На практиці трапляються такі його наближення: гальмування всіх засобів транспорту, початок їх руху з поступовим збільшенням швидкості, вільне падіння тіл, коли вплив опору повітря незначний, тощо. До встановлених кінематичних величин для рівномірного прямолінійного руху (координати, переміщення, шляху, швидкості) в рівнозмінному прямолінійному русі додається прискорення, що характеризує швидкість зміни швидкості. Якщо в початковий момент часу t0 = 1 тіло має початкову швидкість 0, а через певний час t його швидкість дорівнює t, то вектор прискорення прямолінійного рівнозмінного руху можна визначити за формулою:

 

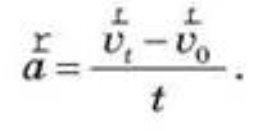
Прискорення — це векторна фізична величина, що дорівнює відношенню зміни швидкості до часу, протягом якого ця зміна відбулася.

Якщо швидкість за будь-які однакові проміжки часу збільшується на ту саму величину, то такий рух називається рівноприскореним. Якщо швидкість тіла зменшується часом на ту саму величину, то рух називають рівносповільненим. Якщо рівнозмінний рух прямолінійний, то за одну з осей координат (наприклад, Ox) зручно взяти пряму, по якій рухається матеріальна точка, а за її додатний напрям — напрям початкової швидкості 0. Тоді прискорення обчислюють як скалярну величину — проекцію вектора прискорення, тому формулу можна записати в скалярній формі:

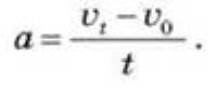
Проекція вектора прискорення матиме знак «+», якщо напрям вектора прискорення збігається з напрямом вектора 0, і знак «-» у випадку протилежного напряму цих векторів. На підставі формули встановлюють одиниці вимірювання прискорення. Як одиницю прискорення в СІ взято прискорення 1 м/с2 - це прискорення такого рівнозмінного руху, під час якого швидкість за 1 с змінюється на 1 м/с.

Для побудови графіка прискорення прямолінійного рівнозмінного руху по осі ординат відкладають прискорення, а по осі абсцис — час. Оскільки під час рівнозмінного руху прискорення не змінюється, то графік прискорення є прямою, паралельною до осі часу. На рис. 1 показано графік прискорення прямолінійного рівноприскореного руху І (а = 2 м/с2) і рівносповільненого II (а = 4 м/с2).

 

 

Рис. 1

 

Із формули прискорення легко визначити миттєву швидкість прямолінійного рівноприскореного руху:

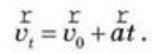
Швидкість рівнозмінного руху є лінійною функцією часу, значення проекції вектора швидкості на вісь Ox:

 

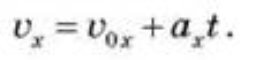
В усіх випадках графіки швидкості прямолінійного рівнозмінного руху мають вигляд прямих ліній, проведених під кутом до осі часу.

Слід мати на увазі, що напрям однієї з осей системи відліку збігається з напрямом вектора початкової швидкості . Якщо вектор прискорення  спрямовано протилежно до вектора , тобто a < 0, значення швидкості t у деякий момент часу може виявитися від’ємним. Це означає, що швидкість t у цей момент часу також спрямовано протилежно до напряму 0.

Середню скалярну швидкість рівнозмінного руху можна знайти як середнє арифметичне початкової 0 і кінцевої t швидкостей у цьому інтервалі часу:

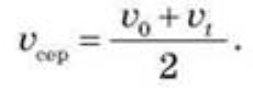
Якщо відомі час і середня скалярна швидкість, то шлях, пройдений матеріальною точкою під час рівнозмінного руху:

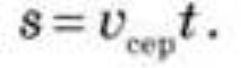
Після підстановки одержуємо:

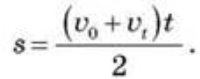
Підставляючи замість t його значення із формули і перетворюючи праву частину рівності, знаходимо вираз шуканого шляху прямолінійного рівнозмінного (рівноприскореного) руху:

 

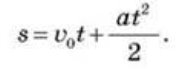
Проекція переміщення під час рівноприскореного руху:

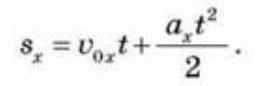
Для знаходження координати х точки в будь-який момент часу t потрібно до початкової координати х0 додати проекцію вектора переміщення на вісь Ox (рис. 5):

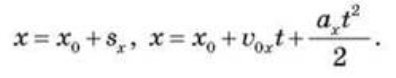
Цей вираз називають рівнянням рівнозмінного прямолінійного руху (кінематичний закон цього руху).

 

 

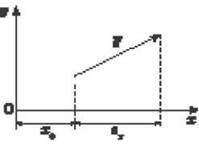
Рис. 5

 

 

Після деяких перетворень дістають рівняння прямолінійного рівнозмінного руху такого вигляду:

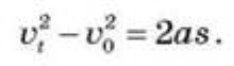
Якщо прямолінійний рівноприскорений рух тіла починається зі стану спокою (0 = 0), то рівняння набуває вигляду:

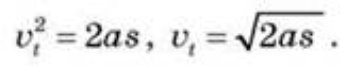
Ці формули часто використовують для розв’язування задач.

 

III. Розв'язування задач, складання конспекту

До конспекту учня

• Миттєвою швидкістю називається швидкість тіла в певний момент часу (або в певній точці траєкторії).

• Прискоренням тіла а називається відношення зміни швидкості тіла до інтервалу часу, за який ця зміна відбулася:

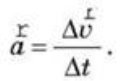
• Прямолінійним рівноприскореним рухом називається рух тіла вздовж прямої зі сталим прискоренням. Під час прямолінійного рівномірного руху швидкість тіла за будь-які рівні інтервали часу змінюється на ту саму величину.

• Швидкість: .

• Проекція швидкості: .

• Проекція переміщення для руху без початкової швидкості:

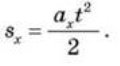
• Проекція переміщення для руху з початковою швидкістю:

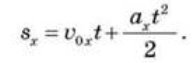
• Залежність координати від часу для руху з початковою швидкістю:

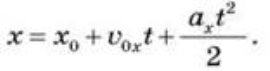
• Середня швидкість:

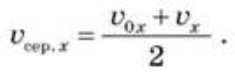
• Співвідношення між переміщенням і швидкістю:

— без початкової швидкості:

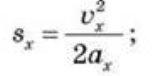
— з початковою швидкістю:

 

 

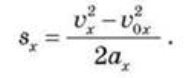
Коментоване розв’язування задачі на дошці

Під час прямолінійного рівноприскореного руху за 10 с швидкість тіла зменшилася з 20 м/с до 10 м/с. Яким є переміщення тіла за цей час? Якою була швидкість через 5 с після початку спостереження?

 

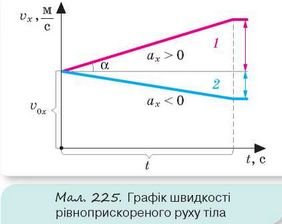
Графік швидкості рівноприскореного руху. Накреслимо графік залежності швидкості від часу v = f(t) для прямолінійного рівноприскореного руху.

Як ми бачимо з формули v_x = v_0x + a_xt, що описує цей рух, між швидкістю й часом існує лінійна залежність, отже, цей графік матиме вигляд прямої лінії (мал. 225). Тангенс кута а між графіком і перпендикуляром до осі швидкості, що проведений через точку v_0x, визначає темп збільшення швидкості:

Що більшою є ця величина, то на більше

значення зростає швидкість за одиницю часу, а отже, більшим є прискорення. За положенням графіка швидкості відносно перпендикуляра до осі швидкості, що проведений через точку v_0x, можна визначити, збільшується чи зменшується швидкість, а отже, і знак прискорення.

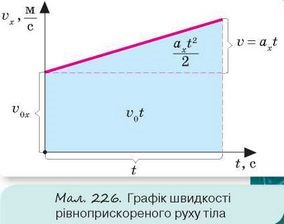
Переміщення в рівноприскорено-му русі. Щоб отримати формулу для обчислення переміщення тіла під час рівноприскореного руху, скористаємося графічним методом, який дозволяє обчислити переміщення тіла як площу фігури під графіком залежності проекції швидкості руху тіла від часу.

Для цього зобразимо графік залежності швидкості тіла від часу для випадку, коли його початкова швидкість v₀ Ф 0 і прискорення a > 0 (мал. 226). У цьому разі модуль переміщення чисельно дорівнює площі трапеції, що утворилася під графіком швидкості.

 

З курсу геометрії відомо, що площа трапеції дорівнює добутку півсуми основ трапеції на висоту. Відповідно, значення переміщення тіла можна обчислити за формулою:

Таким чином, формула для обчислення переміщення має вигляд:

Зауважимо, що в рівноприскорено-му прямолінійному русі, коли тіло рухається, не змінюючи напрямок руху, модуль переміщення дорівнює шляху, який пройшло тіло (s = l), і всі міркування щодо визначення переміщення в однаковій мірі стосуються шляху.

Для розв’язування задач часто застосовується формула залежності переміщення тіла від величини початкової й миттєвої швидкостей (швидкості тіла в певний момент часу). Її можна отримати, розв’язавши систему рівнянь:

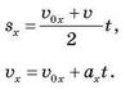
Напишемо друге рівняння відносно часу

і підставимо

в перше. Після алгебраїчних перетворень отримаємо:

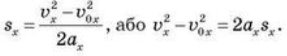
Тепер пригадаємо, що проекція переміщення виражається різницею

з попереднім. Отримаємо

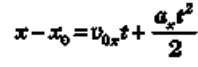
звідки

Цей вираз ще називають кінематичним рівнянням координати для рівноприскореного руху.

Графік переміщення рівноприскореного руху. З курсу алгебри вам відома квадратична функція y = ax² + bx + c, де х — аргумент; а ф 0; b і с — сталі величини.

 

Рівняння переміщення для рівноприскореного руху

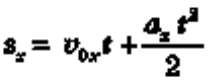
також є квадратичною функцією, де аргументом є час (t), функцією — проекція переміщення (s_x), коефіцієнтом при квадраті аргументу — половинне значення прискорення

що може набувати значення

Коефіцієнт при аргументі b — це початкова швидкість

яка може набувати значення

Графіком квадратичної функції є парабола (мал. 227, а).

гілки параболи спрямовані вгору, за

униз. Що меншим є модуль прискорення (а), то далі відходять гілки графіка від осі переміщення.

Вершина параболи міститься в точці з координатами

Графік координати рівноприскореного руху. Якщо відкладати в певному масштабі по горизонтальній осі (осі абсцис) час, що пройшов з початку рівноприскореного руху, а по вертикальній осі (осі ординат) — значення координати тіла, то одержаний графік виражатиме залежність координати тіла від часу (його також називають графіком руху):

Для рівноприскореного руху графіком руху, як і в разі переміщення, є парабола, положення вершини якої також залежить від напрямів початкової швидкості та прискорення (мал. 227, б). У рівнянні

на відміну від рівняння переміщення, коефіцієнт с ф 0.

За допомогою графіків рівноприскореного прямолінійного руху тіла можна розв’язати основну задачу механіки — визначити положення тіла в будь-який момент часу.

Знання кінематичних величин рівноприскореного руху й уміння їх визначати має надзвичайно важливе практичне значення, адже в житті ми всі є учасниками дорожнього руху (мал. 228).

Формуємо КОМПЕТЕНТНІСТЬ

Я поміркую й зможу пояснити

1. Виведіть залежність переміщення тіла від часу при рівноприскореному русі у випадку а_х < 0.

2. Яке з математичних рівнянь розв’язує основну задачу механіки для рівно-прискореного руху?

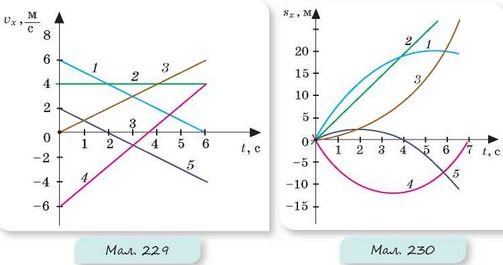
3. Схарактеризуйте рух тіл за графіками залежності швидкості від часу, що зображені на малюнку 229.

4. Схарактеризуйте рух тіл за графіками залежності переміщення від часу, що зображені на малюнку 230.

Вчимося розв'язувати задачі

Під час розв’язування задач слід виконувати певну послідовність дій.

1. Передусім слід вибрати систему відліку, яка складається з тіла відліку, пов’язаної з ним системи координат і приладу відліку часу. Визначити положення тіла в початковий момент часу.

2. Виконуючи схематичний малюнок до задачі, потрібно зобразити систему відліку, вказати напрямки векторних величин (переміщення, швидкості тощо).

3. Установити характер руху (рівномірний чи нерівномірний). Записати кінематичні рівняння (закони) руху для кожного тіла у векторній формі та в проекціях на вибрані осі координат. Урахувати знак проекції вектора на вибрану координатну вісь!

4. За потреби, якщо кількість невідомих більша, ніж кількість рівнянь, — установити додаткові рівняння, які можуть виражати конкретні математичні зв’язки, що випливають з умови задачі.

5. Отриману систему рівнянь розв’язати відносно шуканих величин.

Для графічного розв’язування задачі використовують графіки залежності від часу координат або швидкості (переміщення чи шляху). Це дасть змогу визначати невідомі величини на основі графіків. Слід пам’ятати, що графічні залежності кінематичних величин можуть виявитися корисними як під час аналізу умови задачі, так і для перевірки результатів її розв’язання. На графіках в умовах задач (якщо немає відповідного пояснення) на вертикальній осі відкладено проекцію вектора на вісь ординат.

Графіки кінематичних величин прямолінійного руху

В умовах деяких задач не обумовлено, йдеться про вектор, його модуль чи про проекцію. Аналізуючи умову задачі (або відповідь), треба в кожному конкретному випадку уточнювати, що саме дано в задачі: вектор, його модуль чи проекцію. Зверніть увагу, що модуль векторної величини позначають просто буквою, не ставлячи значка вектора та модуля: замість

Вважається, що рух відбувається вздовж осі, додатний напрямок якої збігається з напрямком руху в початковий момент часу. У деяких задачах, де в умові чи відповіді значення якої-небудь векторної величини наведено зі знаком «мінус», йдеться про проекцію відповідного вектора на вісь координат.

Задача. Кульку штовхнули по похилому жолобу вгору зі швидкістю

Прискорення кульки

Визначте швидкість кульки через 8 с і 16 с

після початку руху.

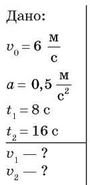
Розв’язання:

Вісь Х направимо вздовж жолоба (мал. 231). Проекція вектора v₀ збігається з напрямком осі Х, оскільки швидкість

зменшується, то вектор прискорення а напрямлений протилежно до осі Х.

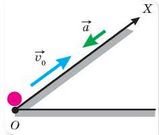
Мал. 231. Рух кульки по похилому жолобу

 

Кінематичне рівняння швидкості

У проекціях на вісь Х з урахуванням знаків проекції векторів

Визначимо швидкість тіла в момент часу

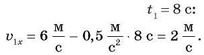
У момент часу t₂ = 16 c:

Знак «мінус» означає, що в момент часу t₂ = 16 c швидкість кульки напрямлена протилежно осі Х, тобто кулька змінила напрямок руху і скочується вниз.

Я можу застосовувати знання й розв'язувати задачі

В права 23

1.

Залежність швидкості від часу в момент розгону автомобіля задано рівнянням v = 0,8t. Побудуйте графік швидкості й визначте швидкість наприкінці п’ятої секунди.

2.

Швидкість поїзда за 20 с зменшилася із 72 до 54 км/год. Напишіть формулу залежності швидкості від часу й побудуйте графік цієї залежності.

3.

Рівняння швидкості руху тіла v = 5 + 4t. Запишіть відповідне рівняння шляху.

4.

Автомобіль за 10 с збільшив швидкість із 18 до 27 км/год. Визначте прискорення і шлях, пройдений автомобілем за цей час.

5.

За який час автомобіль, рухаючись зі стану спокою з прискоренням 0,6 м/с², проїде 30 м?

6.

Гальмовий шлях автомобіля, що рухається зі швидкістю v₁ = 15 км/год, становить s₁ = 1,5 м. Визначте гальмовий шлях s₂ цього самого автомобіля, якщо він рухатиметься зі швидкістю v₂ = 90 км/год. Прискорення в обох випадках однакове.

7.

Тіло рухається прямолінійно й рівноприскорено (а = 3 м/с²). Запишіть рівняння v = v(t) і побудуйте графік цієї функції, якщо початкова швидкість тіла v₀ = 3 м/с.

8.

Рівняння руху тіла має вигляд: х = 0,4t². Напишіть залежність v_x(t) і побудуйте її графік. Заштрихуйте на графіку площу, що чисельно дорівнює шляху, пройденому тілом за 4 с, й обчисліть цей шлях.

9.

Рухаючись із прискоренням 0,3 м/с², лижник з’їхав по схилу завдовжки 100 м за 20 с. Яку швидкість мав лижник на початку й у кінці схилу?

10.

Рухи матеріальних точок задано такими рівняннями: а) x₁ = 10t + 0,4t²; б) x₂ = 2t -1²; в) x₃ = -4t + 2t²; г) x₄ = -t -6t². Напишіть залежність v = v(t) для кожного випадку; побудуйте графіки цих залежностей; визначте вид руху в кожному випадку.

11.

Сноубордист з’їхав з гори, що має схил 40 м, за 10 с, а потім проїхав по горизонтальній ділянці ще 20 м і зупинився. Обчисліть швидкість у кінці схилу, прискорення на кожній ділянці, загальний час руху та середню швидкість на всьому шляху. Накресліть графік швидкості.

12.

Велосипедист перші 4 с рухався зі стану спокою з прискоренням 1 м/с², а потім 0,1 хв їхав рівномірно й останні 20 м, доки не зупинився, — рівносповільнено. Обчисліть середню швидкість за весь час руху. Побудуйте графік v (t).

13.

Відстань між двома зупинками міжміський автобус проїхав із середньою швидкістю v_G = 72 км/год за t = 20 хв. Розгін та гальмування разом тривали t₁ = 4 хв, а решту часу автобус рухався рівномірно. Яку швидкість v мав автобус під час рівномірного руху?

 IV. Домашнє завдання

1. Вивчити відповідний параграф підручника, конспект уроку, формули.

2. Розв’язати задачі.

• За першу секунду рівноприскореного руху без початкової швидкості тіло пройшло 5 м. Яку відстань воно пройшло за перші 3 с? за перші 10 с?

• Поїзд рухається рівномірно і прямолінійно зі швидкістю 50 км/год. Накреслити графік швидкості і показати на ньому модуль переміщення за 3 год. руху.