Дидактичний посібник "Цікава математика".
Відділ освіти Станишівської сільської ради Пісківська загальноосвітня школа І-ІІІ ступенів
(дидактичний посібник)
Піски 2021рік
Розглянуто і схвалено на педагогічній раді Пісківської загальноосвітньої школи І-ІІІ ступенів (протокол № 8 від 20 листопада 2020 року )
Укладач:
Попрійчук Ірина Петрівна – учителька математики Пісківської загальноосвітньої школи І-ІІІ ступенів Станишівської ОТГ, спеціаліст вищої категорії, «старший учитель».
Рецензент:
Солоп Михайло Павлович – директор Пісківської ЗОШ І-ІІІ ступенів, спеціаліст вищої категорії, «старший учитель».
У посібнику вміщено 70 математичних і логічних задач та загадок, зміст яких відповідає чинній програмі для 5 класів загальноосвітніх навчальних закладів.
Призначений для використання вчителями математики, батьками та учнями.
Дидактичний посібник для проведення факультативних занять з математики у 5 класі. Станишівка, 2021. – 32 с.
ЗМІСТ
Вступ ..…..……………………………………………………………………………... 5
1. Текстові задачі ……………………………………………………………………… 7
2. Графічні задачі …………………………………………………………………..… 10
3. Створення малюнків та аплікацій ………………………………………………… 12
4. Задачі на переливання та зважування …………………………………………….. 14
5. Казки та легенди …………………………………………………………………… 17
6. Завдання для проведення квестів, конкурсів .……………………………………. 20
Висновки ……………………………………………………………………………... 21
Список використаних джерел ……………………………………………...………… 22
Додатки …………………………………………………………………………………23 Універсальна математика – це, так би мовити, логіка уяви [яка повинна вивчати]…все, що в ділянці уяви піддається точним визначенням.
Г. Лейбніц
ПЕРЕДМОВА
З розвитком цифрових технологій, комп’ютеризації та діджиталізації зникає необхідність робити власні висновки, шукати прості рішення. Майже будь-які завдання і проблеми можна вирішити за допомогою пошукової системи Інтернет- браузера. Разом з цим виникають інші проблеми: молодь менше логічно мислить. Не шукає власних, легших, особистісно-пристосованих шляхів, а використовує Інтернет-шаблони.
Математична логіка є тим важелем, який змушує мозок дитини краще працювати, допомагає будувати прості умовиводи на основі причиннонаслідкового зв’язку. Ці навички допоможуть їм у різних сферах діяльності дорослого життя [8]. А також сприяють підвищенню самооцінки.
Діти краще сприймають будь-яку інформацію чи щось нове, якщо воно подається в ігровій формі. У віці 11-12 років потрібно розширювати пізнання, але при цьому враховувати ігрові моменти [2]. Наприклад, запропонувати скласти казочку чи оповідання, взявши за основу якісь властивості геометричних об’єктів або правила арифметики. Також можна вивчати математику в картинках: створення малюнків або аплікацій за допомогою геометричних фігур чи помічати оточуючу реальність у цифрах.
Орієнтоване планування занять з математичної логіки та вимоги до навчальних досягнень розміщені у таблиці 1.
Таблиця 1
Орієнтоване планування занять з математичної логіки
|
К-сть годин |
Зміст навчального матеріалу |
Навчальні досягнення учнів |
|
1 |
Вступ. Математика майже без обчислень |
Учень (учениця): - наводить приклади задач логічного характеру; - розв'язує найпростіші задачі логічного характеру. |
|
7 |
Тема 1. Текстові задачі Задачі-жарти. Задачі-загадки. Задачі на уважність. Задачі на кмітливість. |
Учень (учениця): наводить приклади задач логічного характеру на уважність, кмітливість, задач-загадок i задач-жартів; розв'язує такі задачі. |
|
6 |
Тема 2. Графічні задачі Задачі-жарти. Задачі на перекладання сірників. Задачі на додавання та віднімання сірників. Римські цифри з сірників. Геометричні фігури з сірників. |
Учень (учениця): - пояснює, що таке задачі на перекладання сірників; - наводить приклади таких задач; розв'язує нескладні задачі з вірним записом прикладу з римських чисел та на зміну структури фігури. |
Продовження таблиці 1
|
2 |
Тема 3. Створення малюнків та аплікацій за допомогою чисел та геометричних фігур. Графічний практикум. |
Учень (учениця): - розрізняє різні геометричні фігури (трикутники, чотирикутники, інші многокутники); - називає види і властивості даних фігур на репродукціях картин та на власних малюнках. |
|
6 |
Тема 4. Задачі на переливання Задачі на використання двох посудин сталого об’єму та необмеженого резервуару з речовиною. Задачі на використання двох посудин та обмеженого резервуару з речовиною. Задачі на використання трьох посудин. |
Учень (учениця): - пояснює, що таке задачі на переливання; - наводить приклади таких задач; - розв’язує задачі, роблячи при цьому компактний запис у вигляді таблиці. |
|
7 |
Тема 5. Задачі на зважування Визначення легшого (важчого) предмета. Задачі про фальшиві монети. Задачі на обмежену кількість зважувань. Задачі на визначення кількості зважувань. |
Учень (учениця): - пояснює, що таке задачі на зважування; - наводить приклади таких задач; розв’язує задачі на зважування із застосуванням схем. |
|
2 |
Тема 6. Казки та легенди |
Учень (учениця): - розповідає, про що йдеться у тексті; - розрізняє математичних героїв; - складає та розповідає власні казки; - робить висновки |
|
4 |
Повторення, узагальнення і систематизація вивченого за рік |
|
ТЕКСТОВІ ЗАДАЧІ
1. На одному будинку чотири димові труби, на сусідньому три, на наступному дві.
Що виходить в результаті?
2. Двоє батьків і двоє синів спіймали 3 зайця, а дісталося кожному по 1 зайцю. Як це могло трапитися?
3. У хлопчика сестер стільки ж, скільки і братів. Але в кожної сестри братів у 2 рази більше, ніж сестер. Скільки всього дітей у сім’ї? Скільки з них хлопчиків і скільки дівчаток?
4. Електропоїзд їде зі сходу на захід зі швидкістю 60км/год. У тому ж напрямку – зі сходу на захід – дме вітер, але зі швидкістю 50 км/год. У який бік відносить дим поїзда?
5. Колі так набридли мухи, що він вирішив їх переловити. За 4 дні він впіймав 216 мух, до того ж щодня він ловив стільки мух, скільки за усі попередні разом. Скільки мух Толя ловив кожного дня?
6. Як правильно сказати: "9 і 7 буде 15" або "9 плюс 7 дорівнює 15"?
7. На лузі протягом двох годин паслися дві кобили з абсолютно однаковим апетитом. Відмінність між ними була лише в тому, що у одної був хвіст вдвічі коротший. Яка кобила з’їла більше трави, якщо вони почали і закінчили пастись одночасно?
8. Щодня годинник відстає на 6 хвилин. Через скільки днів годинник знову покаже точний час?
9. У 35-річного батька 4 сини з різницею у віці в два роки. Найстаршому зараз 8 років. Коли сумарний вік синів буде рівний віку батька?
10. Написати цифрами п’ятизначне число, що складається з одинадцяти тисяч, одинадцяти сотень і одинадцяти одиниць.
11. Як можна одним мішком пшениці, змоловши її, наповнити два такі ж за розміром мішки, як і мішок, в якому знаходиться пшениця?
12. Мірошник прийшов у млин. У кожному з чотирьох кутів він побачив по 3 мішки, на кожному мішку сиділо по 3 кішки, а кожна кішка мала при собі трьох кошенят. Скільки ніг було на млині?
13. Петрик каже одному: "Я зловив багато великих риб, а маленьких вдвічі менше.
Всього у мене було 16 риб". Це правда?
14. 
Лелеки, зазвичай, у вирій відлітають клином:
попереду один (вожак), за ним два, потім ще два і так далі. Відстань між вожаком і третім рядом становила 6 метрів. Скільки лелек було у клині, якщо відстань між вожаком та останнім рядом становила 18 метрів?
15. Летіли качки: одна попереду і дві позаду, одна позаду і дві попереду, одна між двома і три в ряд. Скільки всього летіло качок?
16. Фермер порахував, що теля коштує вчетверо дорожче за собаку, а лоша – вчетверо дорожче за теля. Взяв 25 тис. гривень і купив собаку, двох телят і лоша. Яка ціна кожної тварини?
17. Двоє пройшли – Три цвяхи знайшли, Слідом четверо пройдуть –
Чи багато цвяхів знайдуть?
18. Два копачі викопують 2м канави за 2год. Скільки копачів за 5год. викопають 5м канави?
19. Що це може бути: дві голови, дві руки і шість ніг має, а для ходьби тільки чотири залучає?
20. У Валиної мами чотири дочки: Марія, Дарина, Катерина. Як звати четверту дочку?
21. Складіть приклади з відповіддю 100. При цьому можна користуватися математичними знаками « + », « – », « · », « : »:
а) п'ять разів цифрою 1;
б) чотири рази цифрою 9;
в) п'ять разів цифрою 5.
Наприклад, "п'ять разів цифрою 3": 33·3 + 3 : 3 = 100.
22. Що це таке: дві ноги сиділи на трьох, а коли прийшли чотири і потягнули одну, то дві ноги схопили три, кинули їх у чотири, щоб чотири залишили одну?
23. У чоловіка запитали скільки йому років. Той відповів, що разом із сином та внуком 121 рік, внук молодший за сина на 28 років, а разом їм 44 роки. Скільки кому років?
24. Син втричі молодший від батька. Коли батьку було 37 років, сину було лише три роки. Який вік кожного зараз?
25. Старший брат сказав молодшому: «Дай мені 8 грн., тоді у мене грошей буде вдвічі більше». А молодший заперечив: «Дай краще мені 8 грн., тоді у нас грошей буде порівну». Скільки грошей у кожного з братів?
26. 
Двоє робітників сіли пообідати. У одного було 4 сендвіча, у другого – 3. Вартість їх була однаковою. Третій робітник попросив поділитись з ним обідом, пообіцявши заплатити за ту частину, яка йому дістанеться. Після обіду, за яким усі їли порівну, він заплатив 21 грн. Допоможіть правильно розділити отримані гроші між двома робітниками.
27. З Житомира і Вінниці, відстань між якими 120 км, назустріч один одному одночасно виїхали два велосипедиста. Один їхав зі швидкістю 15 км/год., а другий зі швидкістю 25 км/год. Разом з велосипедистом із Житомира в той же час вилетіла муха в сторону Вінниці зі швидкістю 20 км/год. Зустрівшись з іншим велосипедистом, муха повертала і летіла у зворотному напрямі, поки не зустріла першого велосипедиста. І так вона літала, поки велосипедисти не зустрілись. Тоді муха сіла перепочити на плече велосипедиста із Вінниці. Скільки всього кілометрів пролетіла муха?
28. 
Пішов батько з чотирма синами в ліс по ягоди. Батько знайшов 45 ягід тоді, коли жодний з його синів, не знайшов жодної ягоди. Роздав батько всі зібрані ним ягоди дітям і всі знову розійшлися по лісу. Коли зібралися йти додому, виявилося, що один із синів знайшов ще стільки ягід, скільки одержав від батька, другий знайшов 2 ягоди, третій дві з'їв, а четвертий, не знайшовши жодної, з'їв половину того, що одержав від батька, після чого виявилося, що в усіх ягід стало порівну. Скільки ягід дав батько кожному з синів?
29. Знайди двоцифрове число, яке у 7 разів більше від числа його одиниць.
30. У класі навчаються 13 дітей. У хлопчиків стільки зубів, скільки у дівчаток пальців на руках і ногах. Скільки у класі хлопчиків і скільки дівчаток. (У кожної дівчинки по 32 зуба, як у дорослих).
31. До Володі на іменини зібрались гості – усі його товариші, і кожен прийшов із своєю сестрою. Якби три дівчинки залишились вдома, то хлопчиків (не рахуючи Вову) було б вдвічі більше ніж дівчат. А якби троє товаришів не прийшли, то було б навпаки. Скільки гостей зібралось у Володі?
32. Скільки кінців у 5 палок? У 4 з половиною палок?
У семи з чвертю палок?
33. На пилорамі щохвилини від колоди відпилюють кусок, рівний десятій частині метра. За який час розпиляють метрову колоду?
34. В сільській школі навчається стільки хлопчиків, скільки й дівчат. Одного разу вчитель приніс 234 горіхи і розділив їх. Кожному хлопчику він дав по 5 горіхів, а кожній дівчинці – по 4. Дівчата образились на таку несправедливість, тому вчителю довелось ще раз принести горіхи і розділити їх так, щоб нарешті усім дісталось горіхів порівну, а саме по 6 горіхів. Скільки всього горіхів приніс учитель?
35. Учневі під час розв’язання задач потрібно було помножити деяке число на 0,5 і до отриманого добутку додати 3. Замість цього він помилково поділив це число на 0,5 і від отриманої частки відняв 3. Не зважаючи на допущені помилки, учень отримав вірний результат. Яке число зустрілось учневі в задачі?
ГРАФІЧНІ ЗАДАЧІ
Графічні задачі можна умовно поділити на згадки із сірниками, використання різних систем числення та задачі з геометричними об’єктами. Такі задачі дітям більше до вподоби, бо мають наочне представлення й учні можуть проекспериментувати для можливості вибору із декількох варіантів одного або кількох правильних [1, 3-5]. 36. Розмістіть 6 сірників так, щоб кожен торкався чотирьох інших.
37.Перекласти сірники так (рис.1), щоб у кожному горизонтальному ряду було: а)
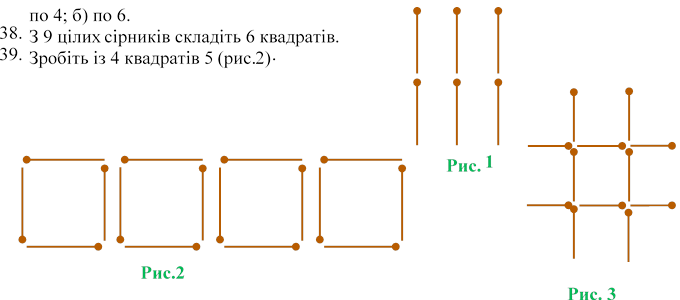
40. Перекладіть три сірники так, щоб вийшло 3 квадрати (рис.3).
41. Покладіть в ряд 10 сірників і складіть з них 5 римських десяток. Переносьте кожен сірник через два сірники. (Уже схрещені сірники рахуються за 2).
42. Виріжте з фігури на рисунку 4 таку частинну, щоб приклавши її до частини, що залишилась, отримати в середині фігури цілий квадрат.
43. Корова на рисунку 5 дивиться ліворуч. Перекладіть два сірники так, щоб вона дивилась праворуч.
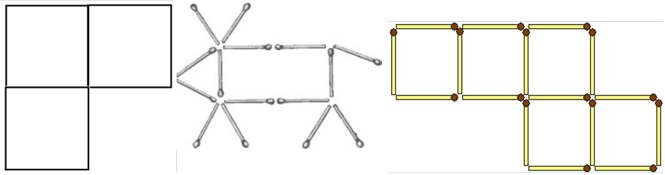
Рис. 4 Рис.5 Рис.6
44. Перекладіть на рисунку 6 два сірники так, щоб отримати 6 квадратів.
45. Складіть із 6 сірників 4 однакові рівносторонні трикутники.
46. Складіть з 9 сірників 4 повністю замкнені чотирикутники.
47. Складіть із 12 сірників 3рівних чотирикутники та 3 рівних трикутники.
48. Будинок складено з 10 сірників. Потрібно перекласти 2 сірники так, щоб він повернувся в інший бік (рис.7).
Рис.7 Рис.8
49. Перемістити один сірник так, щоб отримати правильну рівність (рис.8).
50. Як можна від двадцяти відняти вісімдесят вісім, щоб отримати різницю двадцять два?
51. Оксанка запропонувала Галинці показати на сірниках, що коли від восьми віднімемо п’ять, то нічого не залишиться. Галинка не одразу збагнула, а лише подивившись на настінний годинник. Тоді запропонувала Оксанці свою задачу: створити з одного сірника трикутник, не ламаючи й не розрізаючи його. Подруга не змогла розв’язати цю задачу. Галинка залишилась дуже задоволена. Покажіть, як би ви розв’язали ці задачі.
52. На листку паперу записане число 188. Як його розділити, щоб отримати 100?
53. Перетніть підкову (рис. 9) двома прямими так, щоб розділити її на 6 частин.
Рис.9
СТВОРЕННЯ МАЛЮНКІВ ТА АПЛІКАЦІЙ
Графічний практикум
Створення малюнків та аплікацій за допомогою чисел та геометричних фігур може бути не лише цікавим, а й дуже корисним. В епоху діджиталізації та цифрових технологій, діти не замислюються над властивостями об’єктів, які їх оточують: форма, розміри, математичні та геометричні характеристики. Тому виконання цих завдань, на мою думку, допоможе дитині засвоїти назви основних геометричних фігур. Навчитися зображати ці фігури та краще збагнути, які об’єкти навколишнього світу мають такі форми.
Я вважаю, що почати практикум доцільно з перегляду робіт у стилі кубізму (репродукції, презентація, тощо). Акцентувати увагу слід на геометричних об’єктах, зображених на картині, їх властивостях, композиції, розміщенні та поєднанні. Далі, за допомогою завдань, розміщених у додатках А-1 – Б-8, можна провести практичне заняття із застосуванням креслярських інструментів. Для цього можна використати їх, як шаблони для розмальовок, або ускладнити завдання: запропонувати за зразком створити малюнок або аплікацію. У кожному завданні дитині пропонується завершити малюнки, домалювавши відповідні геометричні фігури (квадрат, трикутник, коло, еліпс, ромб, прямокутник, п’ятикутник, шестикутник). Під час виконання завдання, дитина розвиватиме просторову уяву, логічне мислення та фантазію.
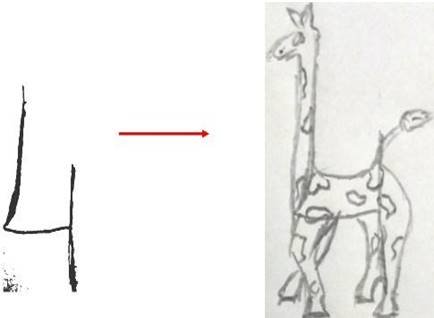Цікавим завданням для дитини буде помітити в обрисах цифри або комбінації цифр якісь живі або не живі об’єкти. Одиндва малюнки, як зразок, має показати вчитель. Потім запропонувати дітям повторити ці малюнки
(рис. 10 - 11).
Наступним кроком має бути створення власних малюнків, включивши свою уяву та фантазію.
Рис. 10
Такі завдання стимулюють розумову діяльність та просторову уяву дитини. Їх можна використовувати для дітей з особливими освітніми потребами.
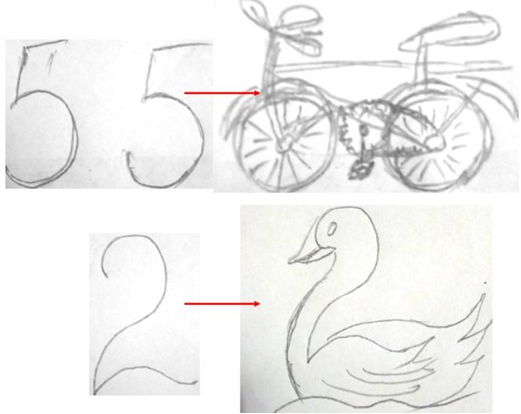
Рис. 11
ЗАДАЧІ НА ПЕРЕЛИВАННЯ ТА ЗВАЖУВАННЯ
У завданнях математичних конкурсів та олімпіад часто пропонують розв’язати задачі на «переливання» чи «пересипання» та задачі на «зважування». Перший тип задач у загальному вигляді можна сформулювати так [11, 14]:
Є дві порожні посудини А і В місткістю, відповідно, а і b одиниць об’єму (можна вважати, що а < b) посудина С місткістю с одиниць (с > а + b). Завдання полягає в тому, щоб у результаті послідовних переливань рідини з однієї посудини в іншу, у посудині В залишилося рівно d (d < b) одиниць об’єму даної рідини.
Слід також врахувати, що правомірними (доступними) є лише наступні чотири типи переливань:
1) З посудини С в посудину А або В можна лити рідину до тих пір, поки вона не наповниться вщерть;
2) З посудини В можна лити рідину в посудину А доти, доки або А не стане повною, або В не стане порожньою;
3) З посудини А можна лити рідину в посудину В доти, доки В не стане повною або не спорожніє А;
4) Усю рідину з посудини А або В можна вилити в С.
Приклади розв’язання задач. Приклад 1. За допомогою 5 л і 7 л посу4дин налити з крану 6 л води?
Алгоритм розв’язання.
Позначити посудину на 5 л – (5), посудину на 7 л – (7). Наповнити (7), перелити з нього 5 л в (5) та ці 5 л вилити, а 2 л, що залишилися в (7), перелити в (5). Наповнити (7), перелити 3 л в (5) та вилити з (5) усю воду, а 4 л з (7) перелити в (5). Наповнити (7), перелити 1 л в (5). У (7) залишилося 6 л, які необхідно було виміряти.
Розв’язання подібних задач доцільно представляти у вигляді таблиць.
Приклад 2. За допомогою 3 л і 5 л банок набрати рівно 1л води (таблиця 2).
Таблиця 2
|
Банки |
|
Переливання |
|
|
|
5л |
— |
3 |
3 |
5 |
|
3л |
3 |
— |
3 |
1 |
Задачі на зважування відрізняються від звичайних задач зі шкільного курсу математики [11,14]. Розв'язання таких задач, полягає в уявленні відповідної ситуації та аналізі всі можливих варіантів. Для цього необхідно скласти алгоритм дій і записати висновки, отримані в результаті виконання.
У задачах на зважування зазвичай іде мова про терези без гир. За допомогою терезів можна лише порівнювати вагу предметів, але не можна встановити їх точну вагу.
Приклад 3. З восьми монет, однаковим номіналом, трьома зважуваннями за допомогою терезів без гир, вилучити одну фальшиву, легшу від інших. Розв’язання.
Ділимо монети на дві рівні кучки – по 4 монети в кожній. Зважимо кучки. Ту кучку, яка легша, знову ділимо на дві однакові кучки – тепер по дві монети в кожній. Знову проводимо зважування. Визначаємо, яка з них легша. Одну монету покладемо на одну шальку терезів, а другу – на іншу шальку. Шалька з легшою монетою підніметься догори.
Приклад 4. Є 9 кг манної крупи. За допомогою трьох зважувань, маючи гирю масою 250 г, розділити крупу у два пакети: в один – 2 кг, у другий – 7 кг.
Розв’язання доцільно подати у вигляді схеми:
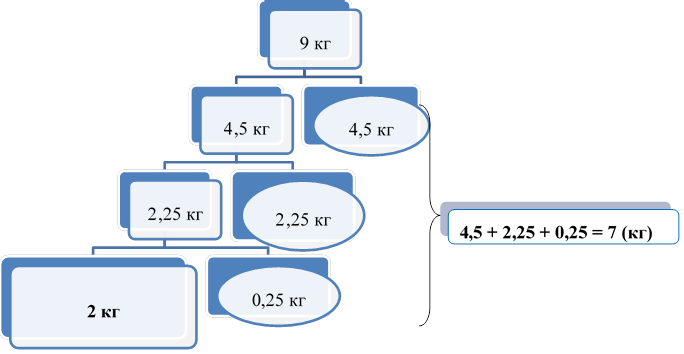
Схема 1 Задачі на переливання
54. Як, використовуючи банки 3 л і 5 л, набрати води рівно 1 л?
55. Як відлити 4 л води за допомогою банок 3 л і 5 л?
56. Як за допомогою двох посудин, що вміщують 5 л і 7 л, налити з крана 6 л води?
57. Яким чином з річки можна принести рівно 6 л води, якщо є тільки два відра: 4 л і 9 л?
58. Маємо три посудини місткістю, відповідно, 8 л, 5 л і 3 л. Найбільша з них наповнена молоком. Як поділити молоко на дві рівні частини, використовуючи ці посудини?
59. Відро місткістю 10 л вщерть наповнене молоком. Є два менші відерця – на 5 і 7 літрів. Як за їх допомогою відміряти рівно 6 літрів молока?
60. У каністрі не менше 10 л дизельного пального. Як відлити з неї 6 літрів, маючи дев’ятилітрове відро і п’ятилітрову банку?
61. Бідон місткістю 10 л наповнений медом. Необхідно перелити з цього бідона 5 л у семилітровий, використовуючи при цьому банку місткістю 3 л. Як це зробити?
62. З повної посудини місткістю 13 л потрібно відлити 7 л гасу, користуючись двома порожніми відрами: 4 л і 9 л. Яке це зробити?
Задачі на зважування
63. Одна з трьох монет фальшива (легша від двох інших, однакових за масою). За допомогою одного зважування на терезах без гир знайти фальшиву монету.
64. 
Серед восьми монет фальшива (легша від інших, однакових за масою). За допомогою трьох зважувань на терезах без гир виділити фальшиву монету.
65. З дев’яти однакових на вигляд монет виділити одну фальшиву (важчу за справжні) за два зважування.
66. У пакеті 3 кг 600 г крупів. Є шалькові терези й гиря 200 г. Як поділити крупи на три пакети: 800 г, 800 г і 2 кг – за допомогою трьох зважувань?
67. У пакеті є 9 кг манної крупи. За допомогою трьох зважувань, маючи гирю вагою 250 г, розділити крупу у два пакети: в один – 2 кг, у другий – 7 кг.
68. У пакеті 9 кг крупи. За допомогою терезів з гирями 50 г і 200 г слід розкласти ці крупи у два пакети: в один – 2 кг, в другий – 5 кг. Спробуйте це зробити за три зважування. Знайдіть два способи розв’язання цієї задачі.
69. Є 4 кавуни різної ваги та різної форми. Як за допомогою терезів, не маючи гир, не більше, ніж за 5 зважувань, розташувати їх за зростанням ваги?
70. Це було під час золотої лихоманки. На одній з копалень добувачі були ображені діями Джо Макдональда – господаря салуна, який приймав від них платню у вигляді золотого піску. Незвичайними були гирі, за допомогою яких він вимірював золото: 1; 2; 4; 8; 16; 24; 32; 64 г. Джо стверджував, що за допомогою цих гир він може зважити з точністю до 1 г. будь-яку порцію золотого піску, вага якого не перевищує 100г. Яку найбільшу вагу можна зважити за допомогою таких гир? Як зважити:
25 г;
48 г;
72 г;
105 г?
КАЗКИ ТА ЛЕГЕНДИ
Винахідливий індус або гра в шахи
Гру в шахи здавна вважають однією зі складних, але разом з тим захоплюючих ігор. Важко сказати, хто винайшов цю гру, так як існує вона вже не одну тисячу років. З цього приводу в індусів є старовинна легенда.
Колись дуже давно жив на світі індійський цар. Все йому в житті вдавалось, все у нього було вдосталь, народ його жив щасливо, але дивна справа: якось придворні стали помічати що їх вельможа сумує. Кожен намагався вигадати щось, аби розважити царя, але нічого не виходило. Цар все одно нудьгував та сумував.
І якось пришов до царя індус та попросив дозволу показати нову придуману ним гру. Цар мимоволі погодився. Але гра виявилась настільки цікавою та на стільки сподобалась государю, що він в захваті вигукнув:
- Якщо твоя голова може вигадати таку гру, то вона заслуговує на винагороду! Проси у мене що захочеш.
- Повелителю, - відповів індус,- я багато не прошу. Накажи своїм придворним покласти одну
зернину пшениці на першу клітинку моєї шахової дошки, дві зернини на другу, чоти на третю і т.д., збільшуючи число зерен вдвічі доти, доки не дійдуть до останньої, 64 клітинки.
- Небагато ти ж просиш,- сказав цар, усміхнувшись від думки, який простий та наївний.
Та всемогутній повелитель індусів не був сильним у математиці! Коли наближені за наказом царя почали здійснювати виплату нагороди, вони швидко переконалися, що ця задача нездійсненна.
Справа в тому, що число зерен, яке попросив індус, є сума ряду з 64 чисел: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192 і т.д. тут записані лише 14 чисел, величина яких відповідає числу зерен, які мають бути покладені на 14 кліток шахової дошки. Решту 50 кліток ще потрібно заповнити! Варто лише подивитися як швидко ростуть ці числа і ви зрозумієте, з якими величезними числами довелося б мати тут справу.
Легенда свідчить, що придворні математики зайнялися підрахунком того числа зерен пшениці, яку довелось би видати винахіднику шахів. З’ясувалось, що якби було можливо засіяти пшеницею всю поверхню земної кулі і збирати врожай щорічно протягом 8-ми років, то і тоді не вистачило б пшениці, щоб сплатити індусу «скромну» винагороду. Ось це число зерен: 18446744070709551615.
Розповідаючи такі легенди, індуси, як великі шанувальники математики, мабуть, намагалися привити таку ж любов до цієї науки й у інших людей. Для цього надавали своїй розповіді таку цікаву форму.
Чарівний світ фігур
В одному мирному містечку математики, жили собі троє найкращих друзів: круг, квадрат та трикутник. Вони дуже любили пригоди, цікаві ігри та ходити до школи. Вони гарно вчилися та дуже любили писати приклади. Одного дня друзі гралися на ігровому майданчику, як за декілька хвилин в містечко приїде новий мешканець. Тільки-но вони дізналися про звістку, всі думали: хто ж це буде? Але з часом вони забули про гостя. А пізніше друзі почули, що сьогодні приїде ромб і згадали гостя, якого вони чекали. За декілька днів вони познайомилися з ним. Їх було вже не троє, а четверо друзів.
За деякий час в них була дуже цікава пригода в цифровому лісі, вони побачили дивного звіра, він був маленький, схожий на мишку. Але це була не мишка, а цифрова жабка, в неї лапки наче одиниці, тіло схоже на нуль, очі – на крапку, а рот – на тире.
А звідки ця жабка і хто її створив, досі не знає ніхто.
Копильців Дмитро, учень 5 класу
Геометричні фігури
Було три брати. Одного звали прямокутний, другого тупокутний, а третього гострокутний трикутник. Всі вони сімейства трикутника. Пішли вони у гості до прямокутного паралелепіпеда. А там зустріли квадрата, куба, циліндра, многокутника, кута, шкалу, відрізок, ламану лінію та круг. Всі вони друзі тому, що геометричні фігури. І тут квадрат величаво сказав:
- Я головний тому, що я красивий, кути прямі і всі сторони рівні!
Круг відповів:
- А я кругленький як м’ячик!
І всі по черзі про себе щось хороше сказали. Тільки відрізок промовчав. Але без відрізка немає геометричних фігур. Тоді хто ж головний?
Габриєлян Богдана, учениця 5 класу
Країна геометричних фігур.
Давно колись жила собі лінія і було їй дуже сумно і одиноко. Вирішила вона помандрувати по світу і знайти собі друзів. Ішла лінія довго-довго і нарешті потрапила у незвичайну країну. Країна ця була зовсім маленькою і жили тут незвичайні мешканці: цифри і геометричні фігури. Побачила лінія чудернацькі многокутники, які мешкали в одному місті і весь час сперечались хто із них кращий: трикутник, прямокутник, квадрат… Поряд жили кути. Ой, які вони смішні! Прямі, гострі, тупі. Вони весь час вихвалялись перед лінією хто із них кращий. Побувала лінія у гостях у цифр. За допомогою цифр вона складала різні приклади і задачі. Їй так сподобалось у цій країні, що вона захотіла залишитись тут назавжди.
Клюсик Назар, учень 5 класу
Країна математики
На краю світу дуже давно була країна математики, і була вона зовсім маленькою. Всього кілька міст. Міста в цій країні були особливі. В одному жили цифри, в іншому знаки, а в третьому геометричні фігури. От ця історія відбулась саме в третьому місті.
Кожна фігура, яка тут жила, була унікальною. І ніхто з мешканців цього міста ніколи не хотів зайняти місце іншої фігури. У трикутника було найбільше прихильників, адже саме з трикутників можна зробити квадрат, прямокутник чи ромб. Навіть пихата трапеція з повагою ставилась до старого і мудрого трикутника. А його молодші шанувальники квадрат, ромб і прямокутник завжди питалися старого вчителя поради.
З іншого боку вулиці жили коло та еліпс. Але найцікавішими фігурами міста, яких всі дуже любили за веселу вдачу, були серце і зіронька. Ці подружки не давали сумувати нікому в місті. Були вони нерозлучними і всі дні і вечори проводили на вулиці. Вдень порівнювали хмарини з фігурами, а ввечері спостерігали за небесними зірками і сперечалися, яка з них сяє найяскравіше.
Ось так і проходило життя в цьому містечку, поки одного ранку не сталася біда.
Коло вирішило зайти до свого сусіда еліпса, а того не виявилося вдома.
- Де ж він може бути? – питали один одного фігури на площі міста.
- Куди він подівся? Його замінити не можна. З двох кіл ніколи не вийде еліпса.
- Висновок один. Треба йти шукати нашого товариша. – сказав трикутник.
- Але де? Але як? – заклопотались сердечко і зіронька.
- За містом. – відповів трикутник.
Всі зібралися біля місцевих воріт. Ніхто з фігур вже й не пригадував, що твориться за межами їхнього міста. Вони ж так давно тут оселилися. Але йти довго не довелось. За кілька кроків від воріт фігури побачили еліпса. Всі так зраділи, що кинувся їм назустріч.
- Де ж ти був? – питались друзі.
- Як же ми без тебе?
І ось що розповів їм еліпс. Він був місцевим вченим і дуже любив читати. От в історії математики кілька днів тому він знайшов повідомлення про старого кута, який брав участь у створенні їхнього міста, а потім переселився до лісу, де мав змогу бачити різних тварин. От еліпс вирішив перевірити чи правда все це.
- І як, знайшов? – поцікавились зіронька з подругою.
Навіть трапеція зацікавлено нагнулася в бік Еліпса, і запитала:
- Така довга і важка дорога до того лісу, що кут запропонував, мабуть, заночувати в нього, і ти погодився?
- Дідусь Кут багато чого цікавого розповів, тому я й затримався. Тепер я частіше його провідуватиму.
- Добре, що ти повернувся, - сказали фігури і пішли на площу міста.
Вони ще мали дослухати розповідь еліпса до кінця. Але це можна зробити й поблизу рідного дому. [15]
ЗАВДАННЯ ДЛЯ ПРОВЕДЕННЯ КВЕСТІВ, КОНКУРСІВ
Сучасним дітям подобається займатися пошуковою діяльністю з використанням різноманітних ґаджетів та віджетів. Для цього у нагоді стануть різноманітні генератори. Умову задачі мовна подати за допомогою QR коду, відсканувавши який, учні зможуть побачити і прочитати умову задачі, яка там зашифрована.
Таблиця 3
Генерування QR кодів до текстових задач
|
Умова задачі |
Графічне представлення задачі |
Посилання на програму для генерування |
|
Діду 56 років, а внуку 14. Коли дід буде вдвічі старший свого внука? |
|
|
|
Запишіть двоцифрове число, яку всемеро більше, ніж число його одиниць. |
|
|
|
Жили собі 2 близнюки. Один щодня спав 1/3 доби, інший ¼ доби. Дожили вони до 72 років. Скільки років проспав кожен? |
|
|
Відповіді або підказки до виконання задач можна подати у вигляді ребуса, який також можна згенерувати за допомогою спеціальної програми, перейшовши за посиланням http://rebus1.com/ua/index.php?item=rebus_generator .
ВИСНОВКИ
Кожен може перетворити вивчення «сухої», на перший погляд, математики у цікаву, захоплюючу гру, принаймні у 5 – 6 класах. Для цього достатньо включити уяву, додати дрібку фантазії і, взявши з собою цей збірник, вирушити у чудовий світ математики. Також ним може скористатися і доросла людина для урізноманітнення свого дозвілля.
Розв’язування задач математичної логіки покращує розумову діяльність дитини, спонукає до встановлення причинно-наслідкових зв’язків та формування логічних висновків, а також підвищує самооцінку. Досвід, отриманий у процесі виконання подібних завдань, може знадобитися й у повсякденні.
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
1. Аменицкий Н.Н., Сахаров И.П. Забавная арифметика. – М.: Наука. Гл. ред. физ.-мат. лит., 1991. – 128 с.
2. Коваленко В.Г. Дидактические игры на уроках математики: Книга для учителя. – М.: Просвещение. 1990.
3. Клименченко Д.В. Задачи по математике для любознательных: Книга для учащихся 5-6 классов средней школы. – М.: Просвещение. 1989
4. Шкільняк С.С. Математична логіка. Приклади задач. Навчальний посібник. –
К.: ВПЦ"Київський університет". 2007
5. Клини C. Математическая логика. – М., 1973.
6. Мендельсон Э. Введение в математическую логику. – М., 1976.
7. Корнієнко М.М., Бєлова Л.П., Полякова Л.Ю. ЛОГІКА+. Математичний калейдоскоп (факультативний курс). 5 клас: Рабочий зошит.
8. Конвенція про права дитини: Міжнародні документи ООН з питань прав людини. – К. 95.
9. https://childdevelop.com.ua/worksheets/5241/
10. https://logiclike.com/uk/tsikava-matematyka/golovolomky-z-sirnykamy
11. https://sites.google.com/site/pidgotovkaolimpiadi/zadaci-logicnogo-tipu/zadaci-naperelivanna-i-zvazuvanna
12. http://rebus1.com/ua/index.php?item=rebus_generator
13. https://qr9.me/free-qr-code-generator.php?lang=uk
14. http://uk.x-pdf.ru/5informatika/1562177-6-informatika-cikavi-zadachi-2-9-klasidruge-vidannya-vipravlene-dopovnene-shepetivka-pp-shestopalov-udk004451-07bbk3.php
15. https://bibl.com.ua/matematika/28341/index.html?page=5
ДОДАТКИ
Додаток А-1 Обчисли та розфарбуй
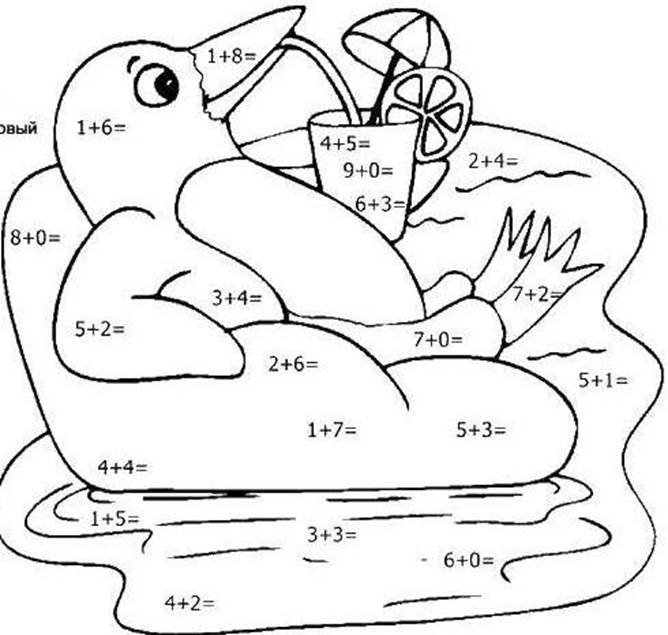
6 – блакитний; 7 – чорний; 8 – фіолетовий; 9 – жовтий Додаток А-2
Обчисли та розфарбуй
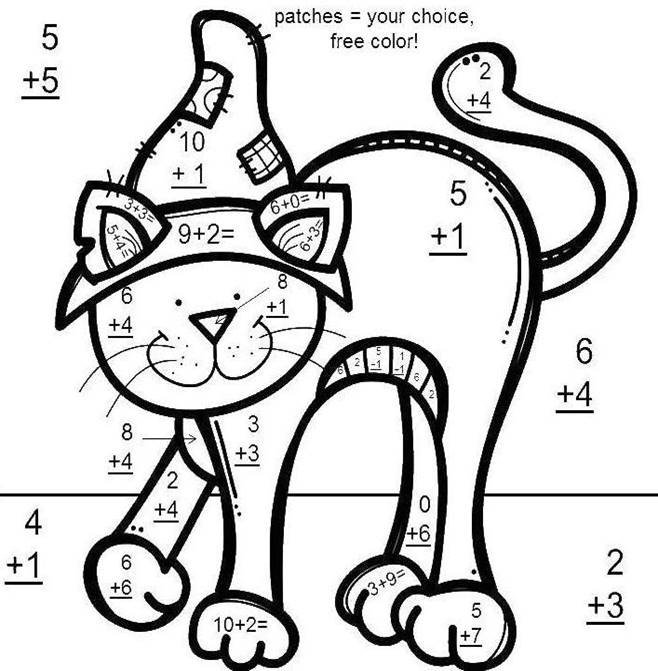
4 – сірий; 5 – зелений; 6 – чорний; 7 – червоний; 8 – жовтий; 9 – рожевий; 10 – блакитний; 11 – салатовий; 12 - білий
-3 Обчисли та розфарбуй
2 – блакитний; 3 – жовтий; 4 – червоний; 5 – зелений
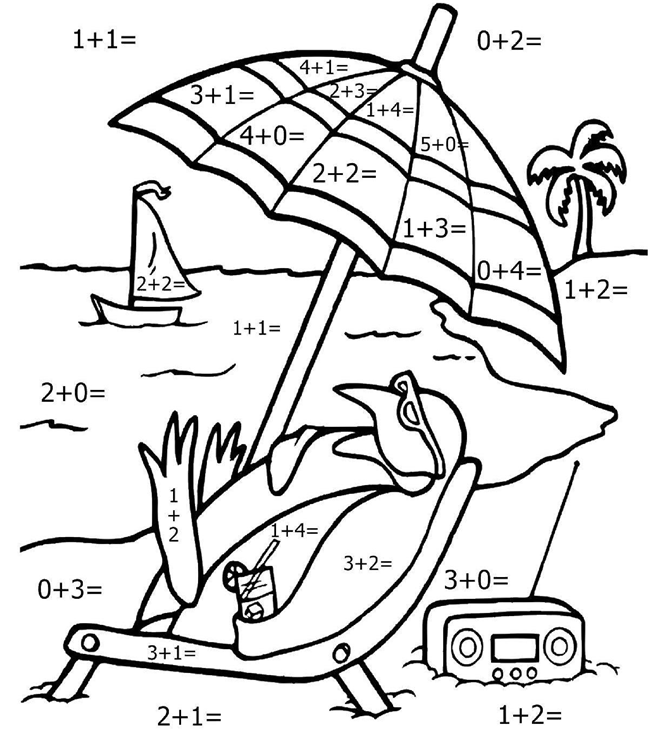
-4
|
0 – білий; 1 – коричневий; 2 – зелений; 3 – жовтий; |
4 – помаранчевий; 5 – блакитний; 6 – червоний; 7 – сірий; |
8 – чорний; 9 - фіолетовий |
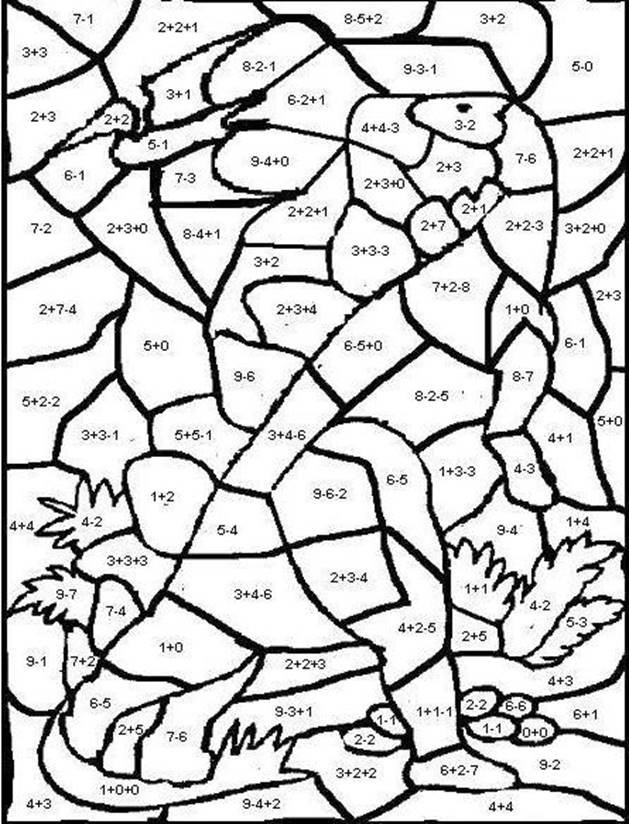
-5 Обчисли та розфарбуй
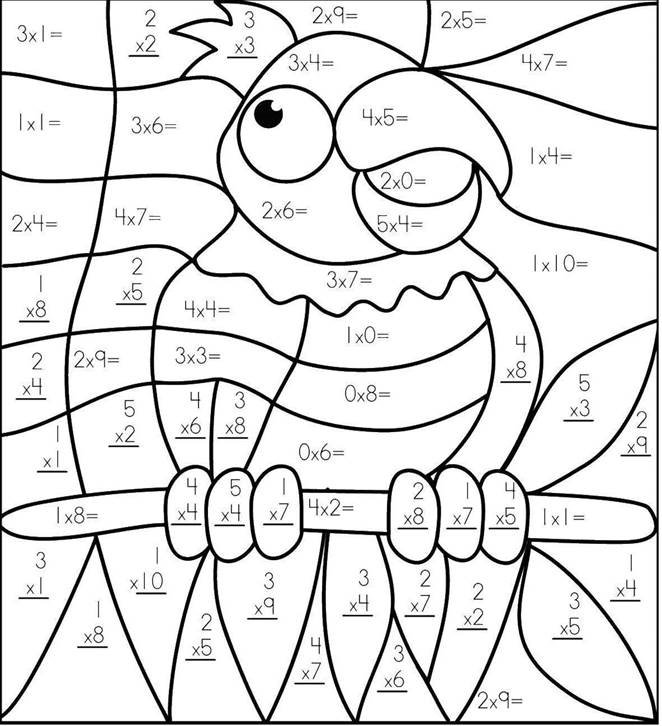
Блакитний – 4, 10, 18, 28; Зелений – 9, 15; Червоний – 0 ; Коричневий – 1, 2, 3, 8; Жовтий – 7, 16, 20; Рожевий – 12, 21, 32; Фіолетовий – 14, 24, 27
-1
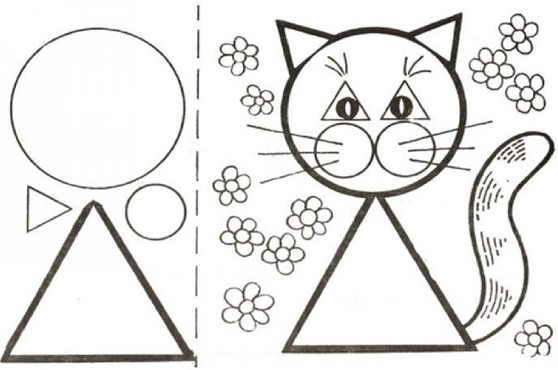
Намалюй котика за зразком, використовуючи геометричні фігури, та розфарбуй малюнок. Запиши назви використаних геометричних фігур
Додаток Б-2
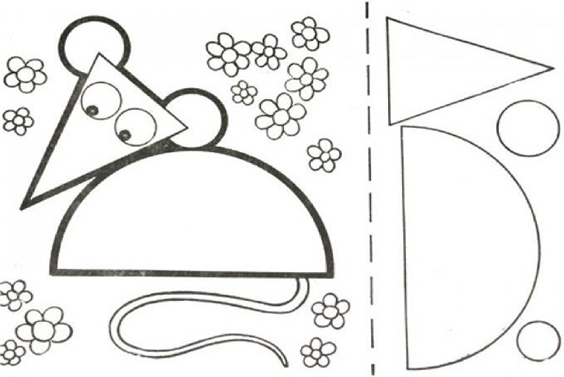
Намалюй мишку за зразком, використовуючи геометричні фігури, та розфарбуй малюнок. Запиши назви використаних геометричних фігур
-3
Намалюй сонечко за зразком, використовуючи геометричні фігури, та розфарбуй малюнок. Запиши назви використаних геометричних фігур
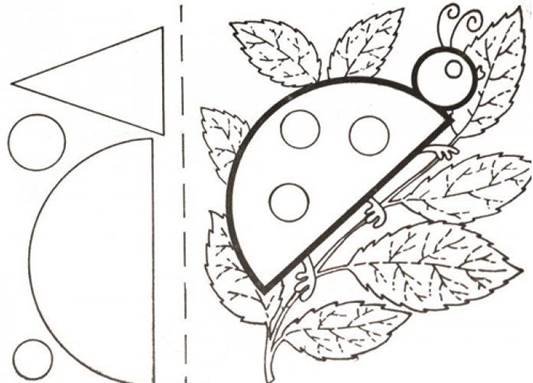
Додаток Б-4
Виріж з кольорового паперу геометричні фігури та створи аплікацію білочки за зразком. Запиши назви використаних геометричних фігур
-5
Виріж з кольорового паперу геометричні фігури та створи аплікацію зайчика за зразком. Запиши назви використаних геометричних фігур
Додаток Б-6
Склади з геометричних фігур аплікацію слоненяти за зразком. Запиши назви використаних геометричних фігур
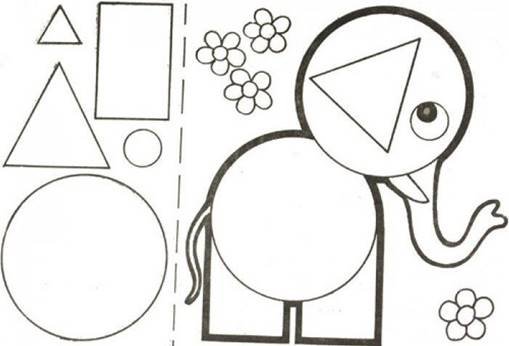
-7
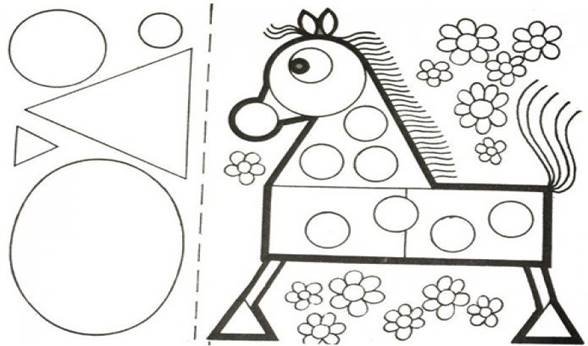
Склади з геометричних фігур зображення коника за зразком. Запиши
назви використаних геометричних фігур
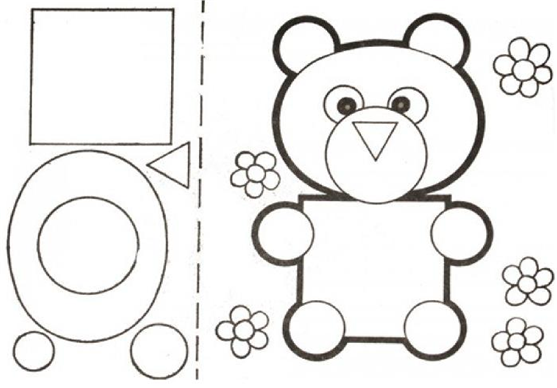
Додаток Б-8
Склади з геометричних фігур аплікацію ведмежати за зразком. Запиши назви використаних геометричних фігур
про публікацію авторської розробки
Додати розробку