Дослідження оптимального коду Шеннона-Фано

 

Дисципліна: «Основи кодування та передавання інформації»

 

МЕТОДИЧНІ ВКАЗІВКИ  ЩОДО ВИКОНАННЯ  ПРАКТИЧНОЇ РОБОТИ

 

«Дослідження оптимального коду Шеннона-Фано»

 

Мета роботи: вивчити властивості оптимальних кодувань, принципи їх побудови; виконати розрахунок параметрів ефективності оптимального нерівномірного коду

 

Теоретичні відомості

 

Одне і те саме повідомлення можна закодувати різними способами. Виникає задача оптимального кодування. Оптимальним вважають такий код, при якому на передавання повідомлення витрачається мінімум часу. Оптимальне кодування застосовується для стиснення (компресії даних), що дозволяє ефективно використовувати пам’ять ЕОМ, виконувати архівацію даних, зменшити тривалість, та збільшити швидкість передачі повідомлень, зменшити дію завад на інформацію.

Якщо на передачу одного символу 0 або 1 витрачається один і той же час, то оптимальним буде код, в якому комбінації записані найменшою кількістю символів. Такий код для кодування повідомлень англійською абеткою був розроблений Клодом Шенноном і Робертом Фано і носить назву коду Шеннона-Фано.

Клод Шеннон - американський електротехнік і математик, «батько теорії інформації». Розвинута Шенноном теорія інформації допомогла вирішити головні проблеми, пов'язані з передачею повідомлень, а саме: усунути надлишковість повідомлень, виконати кодування і передачу повідомлень каналами зв'язку з шумами. Вирішення проблеми надлишковості повідомлення, яке підлягає передачі, дозволяє максимально ефективно використовувати канал зв'язку.

Роберт Фано — італійсько-американський вчений, відомий своїми роботами із теорії інформації.

 

Оптимальним кодуванням називається процедура перетворення символів первинного алфавіту A у кодові слова у вторинному алфавіті B, при якій середня довжина повідомлень у вторинному алфавіті є мінімально можлива  (див. рисунок 1).

 

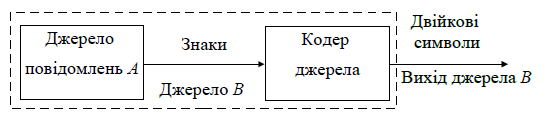
Рисунок 1 – Кодування джерела повідомлень

 

У повідомленнях, що складені з кодових слів оптимального коду, статистична надмірність зведена до мінімуму, в ідеальному випадку — до нуля.

Основна теорема кодування для каналу зв'язку без шумів доводить принципову можливість побудови оптимальних кодів. З неї однозначно витікають методика побудови і властивості оптимальних кодів.

Одним з основних положень основної теореми кодування є те, що при кодуванні повідомлення, розбитого на М-літерні блоки, можна, обравши число символів М достатньо великим, досягти того, щоб середня кількість елементарних символів L_сер  на одну літеру повідомлення, була скільки завгодно близькою до  відношення H/ log₂М.

Різниця  L_сер - H/log₂М  буде тим меншою, чим більше ентропія Н, а ентропія Н має максимум при рівнойомовірних та взаємозалежних символах. Звідси витікають основні властивості оптимальних кодів:

− мінімальна середня довжина кодового слова оптимального коду забезпечується у тому випадку, коли надмірність кожного кодового слова зведена до мінімуму (в ідеальному випадку — до нуля);

−  кодові слова оптимального коду повинні будуватися з рівнойомовірних та взаємонезалежних символів.

З властивості оптимальних кодів витікають принципи їх побудови.

Перший принцип оптимального кодування: вибір кожного кодового слова необхідно здійснювати так, щоб воно містило максимальну кількість інформації.

Другий принцип оптимального кодування: літерам первинного алфавіту, які мають більшу йомовірність, присвоюються більш короткі кодові слова у вторинному алфавіті.

Принципи оптимального кодуванні визначають побудову оптимальних кодів методом Шеннона-Фано.

Побудова оптимального коду за  методом Шеннона-Фано для ансамбля з М повідомлень виконується наступним чином:

а) множину з М повідомлень (символів) розташовують у порядку зменшення йомовірностей (див. таблицю 1);

б) впорядковану за пунктом а)  множину далі розбивають на дві групи таким чином, щоб сумарні йомовірності повідомлень обох груп були по можливості рівними;

в) першій групі присвоюють символ 0, другій – символ 1;

г) кожну з груп ділять на дві підгрупи так, щоб їх сумарні йомовірності були по можливості рівними;

д) першим підгрупам кожної з підгруп знову присвоюють символ 0, другим групам – 1, в результаті чого отримують другі цифри коду. Потім кожну з чотирьох груп знову ділять на рівні (з точки зору сумарної йомовірності) частини і т.д. доти, доки в кожній групі не залишаться по одному повідомленню (символу).

 

Приклад. Побудувати оптимальний нерівномірний код для передавання повідомлень, в яких йомовірності появи літер первинного алфавіту А дорівнюють: p(A_i) = {0,5;  0,25;  0,098;  0,052;  0,04;  0,03;  0,019;  0,011}.

 

Побудову оптимального коду Шеннона-Фано виконуємо за допомогою таблиці 1.

 

Таблиця 1- Побудова оптимального коду Шеннона-Фано

Літе-ра	Йомо-вірності появи літер p(Ai)	Поділ на групи						Кіль-кість знаків ℓі	Кодові комбіна-ції (алфавіт В)	Середня кількість двійк. знаків на літеру ℓі· p(Ai)	Ентропія р(Аi)·log2·p(Аi)
А1	0,50	0	-	-	-	-	-	1	0	0,5000	0,5000
А2	0,25	1	0	-	-	-	-	2	10	0,5000	0,5000
А3	0,098		1	0	0	-	-	4	1100	0,3920	0,3284
А4	0,052				1	-	-	4	1101	0,2080	0,2218
А5	0,04			1	0	-	-	4	1110	0,1600	0,1858
А6	0,03				1	0	-	5	11110	0,1500	0,1518
А7	0,019					1	0	6	111110	0,1140	0,1086
А8	0,011						1	6	111111	0,0660	0,0716
∑	1,00	∑								2,0900	2,0679

 

Перевірка оптимальності коду здійснюється шляхом порівняння ентропії кодованого (первинного) алфавіту А з середньою довжиною кодового слова у вторинному алфавіті В.

Середня кількість двійкових знаків на літеру L_сер  коду А складе:

 

L_сер = ∑ℓ_{i ·} p(A_i) ;                                              (1)

 

L_сер = 1·0,5 + 2·0,25 + 4·0,098 + 4·0,052 + 4·0,04 + 5·0,003 + 6·0,019 +

                  + 6·0,011 = 2,0900 дв.симв.

 

Ентропія Н(А) джерела повідомлень А складе:

 

H(А) = -∑p_i·log_2·p_i ;                                       (2)

 

H(А) = -(0,5· log_2·0,5 +0,25· log_2·0,25 + 0,098· log_2·0,098 + 0,052· log_2·0,052 +                                + 0,04· log_2·0,04 + 0,03· log_2·0,03 + 0,019· log_2·0,019) = 2,0679 дв.симв.

Максимально ефективними є ті оптимальні нерівномірні коди, у яких середня кількість двійкових знаків на літеру L_сер  дорівнює ентропії  Н:

 

H = L_сер.

 

Величина L_сер  точно дорівнює ентропії  Н, якщо довжина рівномірного коду n_і = -log₂ p(A_i) - ціле число.

Якщо довжина коду n_і  не є цілим числом для всіх літер первинного алфавіту (як це є в наведеному прикладі), то

 

L_сер > H,

 

і згідно основній теоремі кодування середня довжина  коду наближається до ентропії  Н із збільшенням довжини кодованих блоків.

З розрахунків (1) та (2) можна сказати, що код В є оптимальним, так як  середня довжина кодової комбінації L_сер є мінімальною і мало відрізняється від ентропії джерела повідомлень Н(А)  (Δ =1,07%).

З таблиці 1 видно, що найбільш йомовірним повідомленням надані короткі комбінації, а повідомленням з малою йомовірністю – довгі комбінації (основний принцип оптимального кодування).

Статистичним оптимальним кодуванням називається кодування, при якому найкраще використовується пропускна здатність каналу без завад.

Ефективність оптимального  нерівномірного коду  оцінюють коефіцієнтом статистичного стиснення К_сс

 

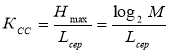,                                          (3)

 

де М – кількість літерного блоку.

 

 

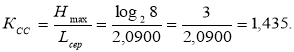
Коефіцієнт  статистичного стиснення характеризує зменшення кількості елементарних символів на літеру  повідомлення в порівнянні з нестатистичним кодуванням.

Щоб показати ступінь використання статистичної надмірності переданого повідомлення розраховується коефіцієнт відносної ефективності К_ВЕ :

 

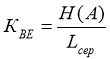.                                                   (4)

 

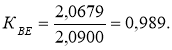
Коефіцієнти статистичного стиснення та відносної ефективності використовуються для порівняння отриманого коду з іншими кодами.

Коефіцієнт надмірності показує, яка частина реального повідомлення є зайвою і могла б не бути передана, якби джерело повідомлень було би організовано оптимально.

Коефіцієнт надмірності джерела повідомлень А складе

 

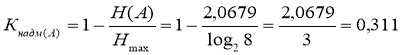.                  (5)

 

Для розрахунку коефіцієнта надмірності джерела В (по виходу кодера) необхідно обчислити ентропію джерела H(B). Для цього знайдемо йомовірності появи символів „1“ і „0“ на виході джерела В:

 

Р(1) = ∑p_i·n_1i /ℓ_i = 0,25·1/2 + 0,098·2/4 + 0,052·3/4 + 0,04·3/4 + 0,03·4/5 + +0,019·5/6 + 0,011·6/6 = 0,294.

 

Р(0) = ∑p_i·n_0i / ℓ_i  = 0,5·1/1 + 0,25·1/2 + 0,098·2/4 + 0,052·1/4 + 0,04·1/4 +

+ 0,03·1/5 + 0,019·1/6 = 0,706.

 

Ентропія джерела В складе:

 

Н(B) =  -∑p_i·log_2·P_i = - (0,294·log₂ 0,294 + 0,706· log₂ 0,706) = 0,874 дв.симв.

 

Тоді коефіцієнт надмірності джерела В складе:

 

 К_надм(В) = 1- H(B) = 1 - 0,874 = 0,126.                         (6)

 

Отримані значення коефіцієнтів надмірності джерел А та В  показують, що оптимальне кодування зменшує надмірність повідомлення.

 

 

Порядок виконання роботи

 

Побудуйте оптимальний нерівномірний код Шеннона-Фано для передавання повідомлень.

Варіанти йомовірностей появи літер первинного алфавіту А занесені в таблицю 2:

 

 

Таблиця 2

Варіант	Йомовірності появи літер первинного алфавіту А
1	p(Ai) = {0,38; 020; 0,14; 0,09; 0,07; 0,045; 0,035; 0,025}
2	p(Ai) = {0,54; 020; 0,09; 0,06; 0,05; 0,03; 0,02; 0,01}
3	p(Ai) = {0,45; 023; 0,18; 0,07; 0,04; 0,03; 0,02; 0,01}
4	p(Ai) = {0,35; 026; 0,17; 0,07; 0,05; 0,04; 0,035; 0,025}
5	p(Ai) = {0,37; 027; 0,16; 0,065; 0,05; 0,04; 0,03; 0,015}
6	p(Ai) = {0,41; 025; 0,135; 0,075; 0,055; 0,035; 0,022; 0,018}
7	p(Ai) = {0,40; 024; 0,155; 0,06; 0,048; 0,04; 0,036; 0,021}
8	p(Ai) = {0,39; 023; 0,165; 0,078; 0,046; 0,038; 0,031; 0,022}

 

Результати побудови оптимального коду занесіть в таблиці 3, 4, 5.

 

Таблиця 3 – Розрахунок оптимального коду Шеннона-Фано

Літера	p(Ai)	Поділ на групи						Кіль-кість знаків ℓі	Кодові комбінації (алфавіт В)	ℓі· p(Ai)	Ентропія р(Аi)·log2·p(Аi)
А1
А2
А3
А4
А5
А6
А7
А8
∑		∑

 

Таблиця 4 – Розрахунок параметрів оптимального кодування

Середня кількість двійкових знаків на літеру коду А, Lсер	Ентропія джерела повідомлень А, H(А)	Максимальна ентропія джерела повідомлень, Hmax	Коефіцієнт статистичного стиснення, КСС	Коефіцієнт відносної ефективності, КВЕ

 

Таблиця 5 Розрахунок коефіцієнтів надмірності джерел

Коефіцієнт надмірності джерела повідомлень А	Йомовірність символів „1“ на виході джерела В	Йомовірність символів „0“ на виході джерела В	Ентропія джерела В	Коефіцієнт надмірності джерела повідомлень В

 

 

Зміст звіту роботи

 

1.               Назва та ціль роботи.
2.               Формули розрахунків.
3.               Таблиці результатів розрахунків.
4.               Короткі висновки з роботи і  відповіді на контрольні питання.

 

Контрольні питання

 

1.               Що називається оптимальним кодуванням?
2.               Основний принцип оптимального кодування?

 

 

Література

 

1.               Беркман Л.Н., Бондарчук А.П., Гайдур Г.І., Чумак Н.С. Кодування джерел інформації та каналів зв’язку :  навчальний посібник. – Київ: ННІТІ ДУТ, 2018.
2.               Фетюхіна Л. В. Теорія інформації та кодування : навч.-метод. посібник/ Л. В.Фетюхіна, О. А. Бутова – Харків: НТУ «ХПІ», 2012.