Конспект уроку школи олімпійського резерву для учнів 7-8 класів на тему: "Теорія подільності в олімпіадних завданнях з математики"
Дана розробка націлена на підготовку учнів до шкільних олімпіад, а також стане корисною для вчителів математики 7-8 класів, так як містить додатковий матеріал з теми:"Теорія подільності".
Учитель ставить на меті: формування понять «подільність націло», «послідовні числа», «розкладання числа за розрядними одиницями» формування вмінь застосовувати властивостей подільності, ознак подільності, вдосконалити навички усної лічби, розширити знання учнів шляхом введення додаткового матеріалу з теми, відпрацьовувати практичне застосування формул скороченного множення; розвивати пізнавальний інтерес до математики, логічне мислення, самостійність; виховувати активність, увагу, культуру математичного мовлення та запису.
ШКОЛА ОЛІМПІЙСЬКОГО РЕЗЕРВУ
(алгебра 7-8 клас)
Підготувала і провела: Лавріненко Тетяна Василівна - вчитель математики Криворізького природничо – наукового ліцею
Тема уроку: Теорія подільності в олімпіадних завданнях з математики
Мета уроку: формування понять «подільність націло», «послідовні числа», «розкладання числа за розрядними одиницями» формування вмінь застосовувати властивостей подільності, ознак подільності, вдосконалити навички усної лічби, розширити знання учнів шляхом введення додаткового матеріалу з теми, відпрацьовувати практичне застосування формул скороченного множення; розвивати пізнавальний інтерес до математики, логічне мислення, самостійність; виховувати активність, увагу, культуру математичного мовлення та запису.
Тип уроку: узагальнення і систематизація знань.
Обладнання: конспект уроку.
Хід уроку
І. Організаційний етап
Вступне слово вчителя. Ми продовжуємо вивчення математики і поглиблюємо знання набуті на уроках. Ще у початковій школі з’явилася така математична дія ділення , на уроках математики 5 - 6 класу розглядалися множини натуральних і цілих чисел і при розв’язуванні певних вправ випливали деякі закономірності, які ми сьогодні узагальнимо і будемо застосовувати на практиці. Попереду на вас чекають нові теореми про властивості подільності цілих чисел, нові ознаки подільності, цікаві задачі.
Бажаю вам подолати перешкоди, які стануть на вашому шляху. Нехай вивчення математики принесе вам радість від одержаних перемог.
II. Актуалізація опорних знань
Історична довідка
Важливе місце в курсі теорії чисел посідає теорія подільності. Цим питанням займалися такі видатні вчені як, Ейлер, Ферма, Б. Паскаль.
П'єр Ферма (1601-1665) - відомий свого часу юрист і радник судового парламенту в Тулузі - інтенсивно і з великим успіхом займався різними математичними питаннями. П. Ферма є одним з творців диференціального числення і теорії ймовірності, але особливо велике значення мають його роботи по теорії чисел. Більшість теоретико-числових результатів П. Ферма записувалися ним на полях екземпляра твору Діофанта „Арифметика”; Ферма зазвичай не записував доведення, а давав тільки короткі вказівки про метод, який він застосовував для отримання свого результату. Існують мала і велика теореми Ферма, які і сьогодні привертають до себе увагу багатьох науковців.
Ейлер дав декілька різних доведень теореми Ферма, з яких перше відноситься до 1736 р. У 1760 р. Ейлер узагальнив теорему.
Блез Паскаль (1623-1662) - видатний французький математик, фізик і філософ. Математичні інтереси Паскаля дуже різноманітні: він зробив істотний внесок у розвиток аналізу нескінченно малих; разом з Ферма Паскаль є засновником теорії ймовірностей; йому належать загальна ознака подільності будь-якого цілого числа на будь-яке інше ціле число, яка ґрунтується на понятті суми цифр числа, а також спосіб обчислення біноміальних коефіцієнтів ("Арифметичний трикутник″ або «Трикутник Паскаля»); він вперше точно визначив і застосував для доведення метод повної математичної індукції
Фронтальна бесіда
- Нагадайте , які числа називають натуральними, цілими?
- Що ви можете пригадати про парні та непарні числа?
- Що означає запис a : b = c?
- Як називають кожен з елементів цієї рівності?
-
Чи мали справу з записом a

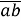 ,
, 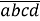 ?
?
III. Узагальнення і систематизація знань
- Подільність націло та її властивості
Зауваження: у всіх формулах цього розділу передбачається, що всі числа належать множині цілих чисел.
Означення: Ціле число a ділиться на ціле число b, якщо існує таке ціле число c, що ![]()
Іншими словами, а ділиться на b, якщо їх частка с знову ж таки є цілим числом. Те ж саме відношення подільності a на b може бути виражене іншими рівнозначними термінами: b ділить a; b – дільник a; a є кратним для b. З означення подільності зрозуміло, що число 0 ділиться на будь-яке ціле число, в тому числі й на 0, але жодне з чисел, відмінних від нуля, на нуль не ділиться. Очевидно також, що будь-яке ціле число a ділиться на a, -a, 1, -1. Ці числа називаються невласними або тривіальними дільниками числа a. Інші ж дільники, якщо вони існують, називаються власними чи нетривіальними.
Позначення: a ![]()
Наприклад: 6 ![]()
![]()
Властивості:
-
a

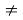
-
0

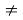
-
Якщо a


-
Якщо a



-
Якщо a



-
Якщо a



Наприклад:
-
5

-
0

-
Якщо 10



-
Якщо 12

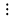

-
Якщо 4




-
Якщо 4






- Ознаки подільності
Ознака подільності - алгоритм, що дозволяє порівняно швидко визначити, чи є число кратним заздалегідь заданому.
Як правило, ознаки подільності застосовуються при усній лічбі.
Розрізняють загальні ознаки, що мають силу для будь-якого m і власні - для окремих значень m.
Загальну ознаку подільності виражає правило, за допомогою якого по цифрах числа N записаного в системі числення з основою g, можна судити про подільність його на інше число m.
Наша мета пригадати відомі вам власні ознаки подільності та сформулювати невідомі.
Ознаки подільності на 2, 3, 4, 5, 6, 7, 8, 9, 10, 11:
- Ознака подільності на 2: Число ділиться на 2 тоді і тільки тоді, коли його остання цифра ділиться на 2, тобто є парної.
- Ознака подільності на 3: Число ділиться на 3 тоді і тільки тоді, коли сума його цифр ділиться на 3.
- Ознака подільності на 4: Число ділиться на 4 тоді і тільки тоді, коли дві його останні цифри становлять число, яке ділиться на 4.
- Ознака подільності на 5: Число ділиться на 5 тоді, коли його остання цифра 5 або 0.
- Ознака подільності на 6: Число ділиться на 6 тоді, коли воно ділиться і на 2, і на 3 (тобто якщо воно парне і сума його цифр ділиться на 3)
- Ознака подільності на 7: Число ділиться на 7 тоді і тільки тоді, коли результат віднімання подвоєною останньої цифри з цього числа без останньої цифри ділиться на 7
Наприклад: 364 ділиться на 7, так як 36 - (2 ∙ 4) = 28 ділиться на 7
- Ознака подільності на 8: Число ділиться на 8 тоді і тільки тоді, коли число, утворене трьома його останніми цифрами, ділиться на 8.
- Ознака подільності на 9: Число ділиться на 9 тоді і тільки тоді, коли сума його цифр ділиться на 9.
- Ознака подільності на 10: Число ділиться на 10 тоді і тільки тоді, коли воно закінчується на нуль.
- Ознака подільності на 11: На 11 діляться ті числа, у яких різниця між сумою цифр, які займають непарні місця, і сумою цифр, які займають парні місця, ділиться на 11.
Наприклад. Число 103785 ділиться на 11, так як сума цифр, що займають непарні місця, 1 +3 +8 = 12 дорівнює сумі цифр, що займають парні місця
0 +7 +5 = 12.
Число 9163627 ділиться на 11, так як сума цифр, що займають непарні місця, є 9 + 6 + 6 + 7 = 28, а сума цифр, що займають парні місця, є 1 + 3 +2 = 6; різниця між числами 28 і 6 є 22, а це число ділиться на 11.
Число 461025 не ділиться на 11, так як 4 + 1 + 2 = 7 і 6 +0 + 5 = 11 а їх різниця 11 -7 = 4 на 11 не ділиться.
Приклади учні наводять самостійно.
Звертається також увага, що за допомогою комбінацій властивостей подільності та застосування декількох наведених ознак подільності одночасно можна отримати нові ознаки подільності.
Наприклад: Число ділиться на 99 тоді і тільки тоді, коли воно ділиться на 9 і 11 одночасно.
Число ділиться на 30 тоді і тільки тоді, коли воно ділиться на 2, 3 і 5 одночасно (або на 3 і 10)
Учням пропонується самостійно сформулювати нові ознаки.
Звертається увага на ознаки подільності на 2, 4, 8 і учні підводяться до нового дослідження, а саме узагальнення ознаки подільності чисел на ![]() .
.
- Послідовні числа
На практиці дуже часто окрім ознак подільності використовують властивості послідовних чисел.
Наприклад: якщо задано два послідовних числа, то одне з них точно парне, а отже можна стверджувати, що їх добуток ділиться на 2;
якщо задано три послідовних числа, то одне з них ділиться на 2 , інше на 3, а отже можна стверджувати , що їх добуток ділиться на 6.
Наведемо приклад запису п’яти послідовних чисел:
n, n+1, n+2, n+3, n+4 або n-2, n-1, n, n+1, n+2
Учням пропонується самостійно дослідити на які числа ділиться добуток таких чисел.
- Розкладання числа за розрядними одиницями
В олімпіадних задачах зустрічаються такі, які мають справу з таким записом ![]() ,
, ![]() або які зводяться до вміння розкладати задане число за розрядними одиницями.
або які зводяться до вміння розкладати задане число за розрядними одиницями.
Запис ![]() означає число, яке складається із цифр a, b і с, і
означає число, яке складається із цифр a, b і с, і ![]() = 100*а + 10*b + с.
= 100*а + 10*b + с.
IV. Практичне застосування матеріалу
Виконання вправ
- Довести, що
-
(
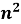 – n)
– n) 
Доведення: У виразі ![]() – n винесемо спільний множник за дужку, отримаємо: n(n-1) – добуток двох послідовних чисел, одне з яких парне, а отже
– n винесемо спільний множник за дужку, отримаємо: n(n-1) – добуток двох послідовних чисел, одне з яких парне, а отже ![]()
![]() – n)
– n) ![]()
-
(
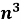 – n)
– n) 
Доведення: У виразі ![]() – n винесемо спільний множник за дужку, отримаємо: n(
– n винесемо спільний множник за дужку, отримаємо: n(![]() -1). Скористаємося формулою скороченого множення для виразу в дужках (необхідно врахувати , що учні 6-ого класу ще не володіють формулами скороченого множення), отримаємо:
-1). Скористаємося формулою скороченого множення для виразу в дужках (необхідно врахувати , що учні 6-ого класу ще не володіють формулами скороченого множення), отримаємо:
(n-1)n(n+1) – добуток трьох послідовних чисел, одне з яких точно ділиться на 2, друге на 3, а отже за ознакою подільності на шість ділиться на 6, з властивості 3 слідує, що (![]() – n)
– n) ![]()
- Довести, що
-
(
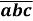 +
+ 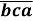 +
+ 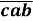 )
) 
Доведення: Розглянемо вираз в дужках і розпишемо його за десятковими розрядами, отримаємо: 100а+10b+с+100b+10с+а+100с+10а+b= =111а+111 b+111с = 111(а+ b+с) . З властивості 3 слідує, що добуток ділиться на 111, а отже (![]() +
+ ![]() +
+ ![]() )
) ![]()
-
(
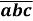 -
- 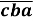 )
) 
Доведення: Розглянемо вираз в дужках і розпишемо його за десятковими розрядами, отримаємо: 100а+10b+с -100с - 10b - а=99а - 99с=99(а-с). З властивості 3 слідує, що добуток ділиться на 99, а отже (![]() -
- ![]() )
) ![]()
- Вік людини в 1973 р. дорівнює сумі цифр її року народження. Скільки їй років?
Розв’язання: Нехай людина народилася в 19xy році (х і у є ![]()
![]() ). За умовою задачі в 1973 році її вік буде 1+9+х+у. Тоді маємо:
). За умовою задачі в 1973 році її вік буде 1+9+х+у. Тоді маємо:
![]() + 1 + 9 + х + у = 1973;
+ 1 + 9 + х + у = 1973;
1000+900+10х+у+1+9+х+у=1000+900+70+3;
11х+2у=63;
х = ![]() ;
;
має виконуватись (63 - 2у) ![]()
1+9+4+5=19 (років)
Відповідь: 19 років.
- Знайти можливі розв’язки , замінивши * цифрою:
-
*74*

Розв’язання: Для того щоб число *74* ![]()
- Остання цифра 0: *+7+4+0=*+11 => *=7
- Остання цифра 2: *+7+4+2=*+13 => *=5
- Остання цифра 4: *+7+4+4=*+15 => *=3
- Остання цифра 6: *+7+4+6=*+17 => *=1
- Остання цифра 8: *+7+4+8=*+19 => *=8
Відповідь: 7740, 5742, 3744, 1746, 8748.
-
3*4*

Розв’язання: Для того щоб число дане число ділилося на 9 необхідно , щоб сума цифр ділилася на 9. Маємо 3+*+4+*=7+*+* => можливі пари цифр: (0;2), (1;1), (3;8), (4;7), (5;6), (9;2)
Відповідь: 3042, 3240, 3141, 3348, 3843, 3447, 3744, 3546, 3645, 3942, 3249.
-
283*64*

Розв’язання: Для того щоб число 283*64* ![]()
-
Остання цифра 0: (0+6+3+2)-(8+*+4)=11-(12+*)= -1-* =>
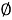
- Остання цифра 5: (5+6+3+2)-(8+*+4)=16-(12+*)=4-* =>4
Відповідь: 2834645
-
*15*

Розв’язання: Для того щоб число *15* ![]()
- Остання цифра 0: *+1+5+0=*+6 => * = 3,6,9.
- Остання цифра 5: *+1+5+5=*+11 => * = 1,4,7
Відповідь: 3150, 6150, 9150, 1155, 4155, 7155
- Шестеро розбійників поцупили більше 10, але менше 100 золотих злитків і почали їх ділити між собою, коли в них 1 злиток залишився було вирішено одного розбійника вигнати і поділити здобич на п’ятьох. І знов поділ не відбувся так як залишився 1 злиток. Так продовжувалося до тих пір, доки не залишився 1 розбійник, який отримав усе собі. Скільки злитків золота було поцуплено?
Розв’язання: З умови випливає, що маємо справу з двоцифровим числом **, яке б без 1 ділилося на 6, 5, 4, 3, 2 => остання цифра 0, перша 6.
Отже 60+1=61 (злиток)
Відповідь: 61 злиток
V. Домашнє завдання
-
Довести, що (
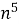 – n)
– n) 
Доведення: n (![]() - n) = n (
- n) = n (![]() - 1) (
- 1) (![]() + 1) = n (n - 1) (n + 1) (
+ 1) = n (n - 1) (n + 1) (![]() - 4 + 4 + 1) =
- 4 + 4 + 1) =
= n (n - 1) (n + 1) ( (n - 2) (n + 2) + 5 ) = n (n - 1) (n + 1) (n - 2) (n + 2) +
+ 5 n (n - 1) (n + 1)
Маємо суму, що складається з доданків:
n (n - 1) (n + 1) (n - 2) (n + 2) – добуток п’яти послідовних чисел => ділиться на 2, 3, 4, 5
5 n (n - 1) (n + 1) – добуток 5 і трьох послідовних чисел => ділиться на 5, 2, 3
Згідно властивостей подільності 3 і 6 випливає, що сума таких доданків ділиться на 30. Що й треба було довести.
-
Довести, що а) (
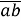 +
+ 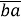 )
) 
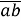 -
- 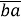 )
) 
-
Знайти можливі розв’язки , замінивши * цифрою: а) 62*742*

б) 187674* ![]()
Відповідь: а) 6267420, 6217425
б) 1876743
1


про публікацію авторської розробки
Додати розробку
