Методична розробка (7 клас) - лабораторна робота: «Дослідження коливань нитяного маятника»

Методична розробка (7 клас) -  лабораторна робота:

«Дослідження коливань нитяного маятника»

    Як відомо з фізики, математичний маятник здійснює гармонічні коливання.

 Формулу для періоду коливань математичного маятника було виведено і перевірено на дослідах голландським фізиком Хрістіаном Гюйгенсом

(1629-1695) і її часто називають формулою Гюйгенса.

•  Період коливань нитяного маятника можливо обчислити за формулою Гюйгенса:

Лабораторну роботу можливо провести і в домашніх умовах, як це показано на фото 1. На фото 2 показано повне відхилення кульки

 Для виконання лабораторної роботи в фізичному кабінеті - дослідження коливань нитяного маятника необхідно слідуюче обладнання: 

•  штатив;

•  лапка;

•  металева кулька з наскрізним отвором;

•  терези; 

•  нитка, довжиною 50 – 60 см;

•  лінійка;

•  сірник (дерев’яна паличка);

*              За допомогою терезів виявимо масу металевої кульки з дерев’яною паличкою в отворі – вона становить 19 г (в принципі, кулька може мати і іншу масу).

*              Пропускаємо нитку крізь отвір в кульці і фіксуємо за допомогою за допомогою дерев’яної палички, проводимо вимірювання довжини нитки – до кульки. 

*              Закріплюємо лапку на певній висоті на штативові, підвішуємо нитку з кулькою так щоб між столом і кулькою була деяка відстань в стані спокою.

Таким чином підготовка до проведення дослідів закінчена. 

•  Відводимо кульку вліво на деякий кут і відпускаємо нижній кінець нитки. • Вмикаємо секундомір в момент відпускання кульки і вимикаємо секундомір на десятому повертанні кульки в лівий бік – фіксуємо час за 10 коливальних періодів;  • Обчислимо період Т коливального руху кульки за формулою:

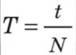    де: t – час; N – кількість коливань.

•  Обчислимо частоту n коливального руху кульки за формулою:

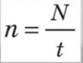 де: t – час; N – кількість коливань.

   Наведемо приклад виконання лабораторної роботи. 

Нитяний маятник з довжиною нитки 0,36 м робить 10 коливань за 12 с, тобто період коливань становить 1,2 с.

При  довжині нитки 0,36 м і визначеному періоді 1,2 с розрахунок n становить: n = 10/1,2 = 8,33 – частота коливального руху.

Зробимо розрахунок для періоду коливань: 

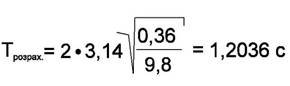
Значення Т_{розрах.} близьке до виміряного. Проведемо розрахунок відносної похибки вимірювань при проведенні досліду. 

Ԑ = |1 -  Т _{розрах.} /Т _вим.| × 100% = = |1 -  1,2036/1,2| × 100% = 0,3%.

Завдання для відмінників: 

«Визначення прискорення вільного падіння за допомогою нитяного маятника»

• Період коливань нитяного маятника можливо обчислити за формулою Гюйгенса:

Звідки знаходимо g і отримаємо потрібну формулу:

   Зрозуміло, що не варто брати для розрахунку Т_{розрах.} , бо при цьому завідомо отримаєм 9,8 м/с² – візьмемо для розрахунку g – T_вимір. = 1,2 с.

При  довжині нитки 0,36 м і визначеному періоді 1,2 с розрахунок g становить: g = (2 • 3.14)² • 0,36 / (1,2)² = 9,86 м/с²

 Розрахунок відносної похибки Ԑ = |1 – g_дійсне /g _{розрах.|} × 100%  = = |1 -  9,8/9,86| × 100% = 0,6%.   

   Відносна похибка становить 0,6%, що цілком допустимо. 

  Зрозуміло, що при іншій довжині нитки буде інший період коливань.

Висновок: згідно довідника з фізики, g = 9,8 м/c² має планета Земля. 

   Слід зауважити, що в різних місцях Землі g може трохи відрізнятись. Прискорення вільного падіння не однакове скрізь на Землі. Стандартне значення приблизно відповідає прискоренню падіння тіла на широті 45° і на висоті рівня моря.Відхилення від стандартної величини обумовлено низкою причин:

•  Обертанням Землі. Внаслідок обертання Землі, завдяки дії доцентрової сили, прискорення вільного падіння тіла на полюсах вище, ніж на екваторі.

•  Формою Землі. Земля неідеальна сфера, а має сплюснуту на полюсах форму.

•  Висотою над рівнем моря.

•  Неоднорідністю Землі.

Так, для прикладу, для 

Києва g = 9,81054       

            м/с², а для               Фото 1                                          Фото 2                         Миколаєва                                                                                                         g = 9,80781 м/с², а в районі екватора ця величина дорівнює 9,83 м/с².

У звіті необхідно проаналізувати експеримент і його результати.

Література:  

1. Автор: Бабин Дмитро Святославович, Інтернет,

https://radioelectronics-ur5ydn.jimdofree.com/7-клас-лабораторні-роботи-зфізики/  

Автор: Бабин Дмитро Святославович