Навчальний проект з математики для учнів 5 класу "Салон краси чисел"

Навчальний проект

учнів 5-Б класу ЛНВК «ЗОШ І-ІІІ ст. №22 – ліцей»

Керівник проекту:

вчитель математики Герус Олена Адамівна

Мета проекту

• детальніше ознайомлення учнів з властивостями чисел, їх цікавими особливостями;
• розширення наукового кругозору;
• формування інформаційної компетентності;
• розвиток інтересу до вивчення математики

Актуальність проекту

 Розширення кругозору школяра є завше актуальним. Кожне число має свою цікавинку. Працюючи над проектом, дізнаємося багато цікавих і корисних фактів про числа, які надалі можна використати під час навчання, підготовки до олімпіад.

Методи отримання інформації: літературні та електронні джерела.

Результати: підготовка повідомлення, створення презентації, виступ перед учнями 5-х класів.

 

Використані джерела

1. Красота в квадрате. Как цифры  отражают жизнь и жизнь отражает цифры / Алекс Беллос; пер. с англ. Н. Яцюк.  ‒ М.: Манн, Иванов и Фербер, 2015. ‒ 368 с.

2.https://ru.wikipedia.org/wiki/142_857_(%D1%87%D0%B8%D1%81%D0%BB%D0%BE)

  3. http://hijos.ru/chislovoj-salon-krasoty/chislo-22/

  4. http://aboutnumber.ru/2018

  5. https://zaxid.net/vcheni_oksfordskogo_universitetu

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

У нашому житті особливе місце займають числа. Не дивно, адже  ми на кожному кроці стикаємося з ними. Вони супроводжують людей від самого народження і до смерті. Без чисел сьогодні вже не можливо уявити нашого життя.  Вони служать нам як інструменти для підрахунку, обчислень і встановлення кількості об’єктів. Більше того, у нас виникають ще й певні почуття у ставленні до них: є  числа, які викликають симпатію і які – антипатію, є улюблені числа і не дуже. На світі є безліч людей, які, проводячи маніпуляції з числами, отримують естетичну насолоду, бачать їх красу.

Тому ми вирішили відкрити «Салон краси чисел» і розмістити там числа, які ми вважаємо привабливими.

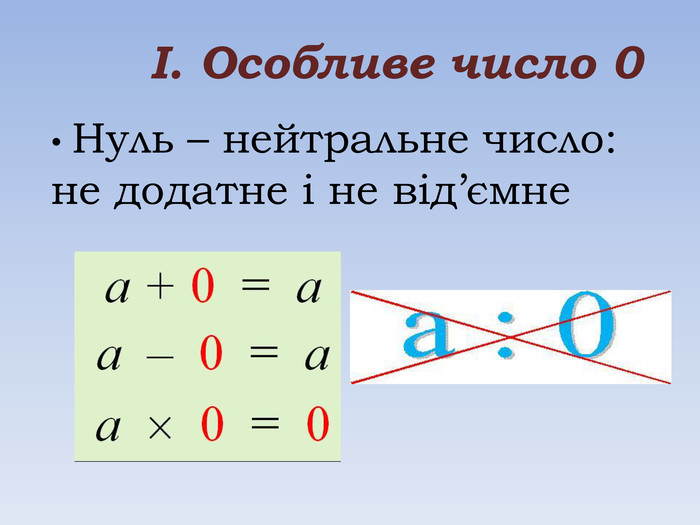
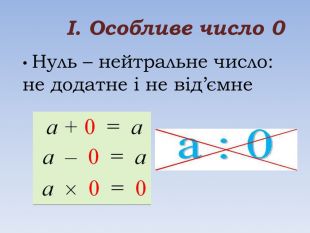
Один з експонатів  нашого салону – число нуль. Нуль відомий як нейтральний елемент.

Вчителя спитали діти:
«Нуль – це як? Навіщо він?»
Аби цифру зрозуміти,
Я вам дещо розповім:
«Нуль – коли цукерки зїли,
Птаство в вирій відлетіло.
В зоопарку нуль ведмедів?
Сторож клітки не догледів».
Діти граються, сміються,
Роздивляються на блюдце:
Щойно печиво поїли,
Навіть крихти не лишили,
Значить, нуль, або нічого
Не зосталося смачного.

Незважаючи на свою «пустоту», нуль став основою сучасної математики, адже програмісти починають рахувати з нуля. Нерідко можна почути фразу « це сума  з багатьма нулями».  Дивовижно, що саме нуль, характеризуючий ніщо, демонструє величину і масштабність грошових цінностей.

У вересні 2017 року медіа видання обійшла новина: Британські вчені з Оксфордського університету виявили в одному з давніх індійських манускриптів найдавніше в історії письмове позначення нуля.

Як зазначається, відкриття зробили під час вивчення так званого «манускрипту Бакшалі» - одного із найдавніших прикладів вирішення математичних задач. Старовинний документ з берести знайшли у 1881 році на території сучасного Пакистану. Він містить 70 сторінок і вважається одним з найдавніших документів в історії індійської і світової математики. Рукопис написаний однією з форм санскриту. З початку XX століття його зберігають в бібліотеці Оксфордського університету.

Через крихкість сторінок учені досі не могли точно визначити час, коли він був написаний. Аналіз стилю письма і зміст вказували на те, що документ був створений у IX-XII століттях, але нещодавній радіовуглецевий аналіз артефакту дозволив датувати манускрипт щонайменше на 500 - 600 років раніше: II-IV століттями нашої ери.

У документі знайшли багато позначок нуля. Символ, що зустрічається в манускрипті Бакшалі, не ідентичний сучасному. Він виглядає, як суцільна окружність. Порожній простір усередині округлого символу в індійських текстах з'явився вже пізніше. Крім того, нуль рукопису Бакшала не виступає в якості самостійного числа, а слугує заповнювачем.

Наприклад, у числі 101 він вказує на відсутність десятків. Проте вчені вважають, що саме ця форма нуля потім стала основою сучасного розуміння цього числа. Зазначимо, до цього вважалось, що найдавнішим згадуванням нуля є настінний напис в храмі індійського міста Гваліор - написане там число 270 датується кінцем IX століття.

Близько 1770 р. до н. е. єгиптяни  позначали нуль  ієрогліфом, що означав «красивий». У центрі міста Будапешт (столиця Угорщини) стоїть пам’ятник нулю. Від цього пам’ятника відмірюються всі відстані в країні.  Наскільки нам відомо, це єдиний пам’ятник числу.

 

Цікаво, що жест рукою, який зображає цифру 0, в англомовних країнах

 означає «все в порядку»

***

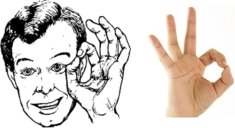
Настав 2018 рік, і нас зацікавило число 2018. Ось які факти про це число зберігаються в нашому салоні. Його сума цифр 11.

Воно має лише чотири дільники: 1, 2,  1009, 2018 . Сума дільників 3030.

Запис у римській нумерації MMXVIII. У двійковій системі числення 11111100010. 2018 байтів це 1 кілобайт 994 байта.

2018 належить до напівпростих  чисел – дорівнює добутку двох простих чисел (2 і 2009). (Просте число має лише 2 дільники: одиницю і саме це число).

Ми зацікавились напівпростими числами і з’ясували, що їх послідовність  починається так:

4, 6, 9, 10, 14, 15, 21, 22, 25, 26, 33, 34, 35, 38, 39, 46, 49, 51, 55, 57, 58, 62, 65, 69, 74…   Крім того, ми дізналися, що найбільше відоме напівпросте число станом на  лютий 2010 року дорівнювало (2^43112609 − 1)², десятковий запис цього числа складається більш ніж з 25 мільйонів цифр. Воно є квадратом найбільшого відомого простого числа.

Для власників смартфонів ми встановили , який  QR-код числа 2018:

***

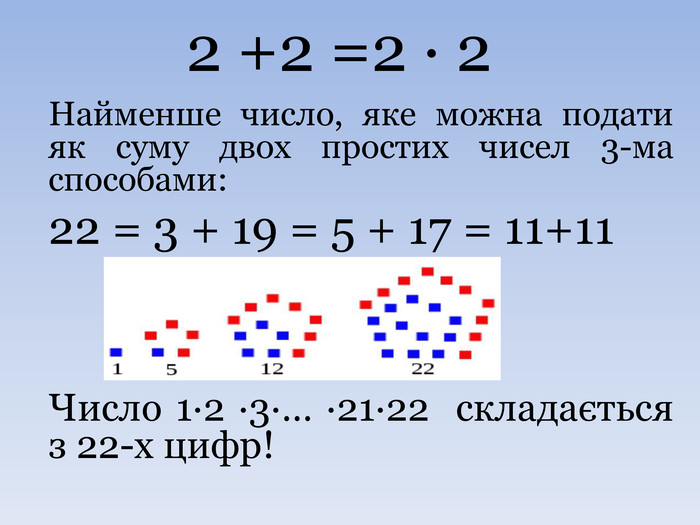
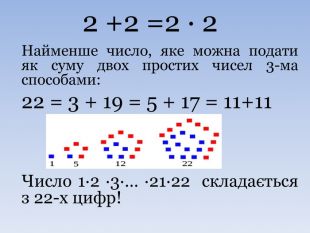
Номер нашого закладу – 22.  Ось які факти ми зібрали про число 22.  Це єдине двоцифрове число, у якого сума цифр дорівнює їх добутку,  2·2 = 2 + 2. Також це числовий паліндром (читається як справа наліво, так і зліва направо)

22 - найменше число, яке можна подати у вигляді  суми двох простих чисел трьома різними способами, с точністю до порядку доданків (3+19, 5+17, 11+11). Якщо число АВС парне, то число  виду АВСАВС ділиться на 22 без остачі. Наприклад, 134134: 22 = 6097. Пояснюється це тим, що

 134134 = 134·1001 = 67·2·11·13·7. Число 22 –  фігурне п’ятикутне число.

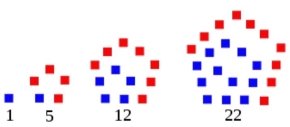
22 березня  відзначають Всесвітній день води. Він запроваджений Генеральною Асамблеєю ООН в 1993 році. Цікаво, що 1+ 9 + 9 + 3 = 22. 

Якщо знайти добуток 1·2·3·… ·21·22, то виявляється, що в цьому числі 22 цифри!

***

Перейдемо до дуже екзотичного  експоната – числа 142 857. Що в ньому особливого, запитаєте ви.  Ось посудіть самі. Якщо це число множити на   2, 3, 4, 5 чи 6, результати будуть утворені циклічним зсувом самого числа 142 857:

1 × 142 857 = 142 857	4 × 142 857 = 571 428
2 × 142 857 = 285 714	5 × 142 857 = 714 285
3 × 142 857 = 428 571	6 × 142 857 = 857 142
	7 × 142 857 = 999 999

Результати ділення числа на 2 чи на 5 також можна отримати зсувом:

142 857 : 2 = 71 428,5

142 857 : 5 = 28 571,4

Якщо число розбити на дві трійки, піднести отримані числа до квадрата та відняти добутки, то знову отримаємо результат зсуву числа:

857² =734449,  142² =20164,   734449 – 20164 = 714285.

{\displaystyle 857^{2}=734449}1/7 = 0.14285714285714285714…

Якщо десятковий запис числа 142 857 розбити на дві трійки 142 і  857 та додати, то вийде 999, а якщо розбити на три двійки і додати, то вийде 99! Крім того виконуються такі рівності, які можна вважати магічними:

142857² = 20 408 122 449, 142857 = 20 408 + 122 449.

142857 = 5291· (1 + 4 +2 + 8 + 5 +7).

***

На безкраїх числових просторах  ми виявили чотири дивовижних десятизначних числа, які стали  особливими екземплярами нашого салону:

2 438 195 760

4 753 869 120

3 785 942 160

4 876 391 520

У кожному з цих чисел є всі цифри від 0 до 9, кожна цифра лише по одному разу, і кожне з цих чисел ділиться (увага!) на 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17 і 18!!!

***

У  нашому салоні розміщено не тільки натуральні числа, а й дробові. Те, що вони є привабливими  для людини, свідчить вірш, складений про них.

     У твоєму задачнику

Якось-то прохали :

Давайте прогуляємось ми у вечірній час.

Ах, що ви, , –   зам’ялись .

А якщо зненацька стрінуть нас?

Хай бачать  , –  сказали .

Мені це, , повірте, все одно!

Хай знають  ,–  гукнули ,

Що я вас, , люблю уже давно!

І я вас, ,–  зізнались .

Ходімо , , подайте ж бо пальто.

    Ну що нам  !

   Ну що нам !

    Ну що нам

    І навіть цілих сто!

Сподіваємось, що наш салон буде поповнюватись і яскраво демонструватиме красу цих знайомих незнайомців – чисел!

 

Висновки

Числа – це символи, за допомогою яких виражаються кількісні співвідношення навколишнього світу. За висловом видатного математика Г.Лейбніца, «число висвітлює глибину світобудови». Гармонія чисел, їх різноманітних строгих і жартівливих,  корисних і курйозних властивостей, милозвучність їх цифрових конфігурацій – це краса  закономірностей Природи. «Тим, хто не знає математики, – вважав американський фізик, лауреат Нобелівської премії Р. Фейнман, – важко відчути красу, найглибшу красу природи». Пошук «математичних перлин» робить заняття математикою не просто корисним , а й приємною справою для душі.