Нетрадиційні форми навчання

Міністерство освіти і науки України

 

 

 

 

 

 

“НЕТРАДИЦІЙНІ ФОРМИ НАВЧАННЯ”

 

 

 

 

 

 

Вчитель математики

Мирогощанського ліцею

Мельничук Інна Анатоліївна

 

 

2024 рік

 

ЗМІСТ

 

1.               Вступ
2.               Урок як основна форма організації навчання
3.               Нетрадиційний урок «Подорож до Країни раціональних чисел»
4.               Ефективність застосування нетрадиційних форм навчання.
5.               Висновок
6.               Список літератури

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВСТУП

Нова українська школа – це школа, до якої приємно ходити, цікаво і весело навчатися, де можна отримати знання і навчитися їх застосовувати в житті. Тому посилаючись на концепції НУШ в умовах реформування освіти, інтенсивного переосмислення духовних і моральних цінностей, подолання консерватизму і стереотипів педагогічного мислення значну увагу приділяю питанням впровадження в практику роботи нетрадиційних форм організації навчальних занять. Намагаюся уроки математики зробити цікавими, сучасними з використанням нестандартних методів роботи, що допоможе дітям краще зрозуміти вивчення математики. Вважаю, що це дає можливість зробити урок цікавим, підвищити інтерес учнів до вивчення предмета, активізувати їх діяльність та зняти напруження, особливо під час перевірки знань.

Великий французький математик Сімеон Пуассон колись сказав: «Життя прекрасне двома речами: можливістю вивчати математику й можливістю викладати її» [1]. Тому я ставлю собі за мету подбати про те, щоб зацікавити учнів математикою і для всіх, хто хоче її пізнати, зробити цікавою і доступною. Для досягнення цієї мети приділяю увагу не лише навчальній діяльності, а й ігровій, оскільки завжди вважалося, що елемент зацікавленості полегшує навчання. Особливо це стосується роботи у 5 – 6 класах, де навчання має свою специфіку і представляти його треба як забаву, а не як нудну необхідність.

Я застосовую різноманітні уроки: урок – ярмарка, урок – подорож, урок – аукціон, урок – квк. Велику увагу приділяю позакласній роботі та роботі з обдарованими дітьми. Традиційними в школі є тижні математики, ігри «Щасливий випадок», «Що? Де? Коли?», брейн – ринги, математичні ярмарки.

Завданням такої форми роботи є різносторонньо розвивати особистість, формувати навички та вміння, стимулювати концентрацію уваги учнів на уроці. Учні серйозніше ставляться до навчання, постійно з’ясовують незрозумілі питання.

Використання нестандартних методів на уроках математики різносторонньо розвиває особистість і звичайно кінцевий результат діяльності вчителя – новоутворення в особистості учня.

Кожен учитель має нести відповідальність за те, якими учні вийшли з його уроку. Тобто після уроку в дітей не повинна згаснути жага до знань і любов до життя.

На уроці учень має здобувати знання і вчитися ними оперувати, витрачаючи на це лише частку своїх сил. Відомо, що діти йдуть до школи за спілкуванням з друзями, з учителем. Найбільшу радість і задоволення вони повинні отримувати від роботи на уроці, що дозволяє відкрити себе, свої задатки, здібності тощо. Розкрити особистість учня можливо, якщо учитель йтиме на урок не тільки зі знаннями навчального матеріалу, методів і прийомів навчання, а й з різноманітними і цікавими способами та прийомами організації праці учнів. У зв’язку з цим сучасний вчитель шукає нові ефективні засоби і методи навчання, такі методичні прийоми, які активізували б думку школярів, стимулювали б до самостійного здобуття знань. Найтиповіші методи і форми роботи з учнями необхідно застосувати у комплексі з нестандартними підходами, які можуть посилювати інтерес школярів до навчання. Уроки, які за формою не зовсім вкладаються в рамки виробленого і сформульованого дидактикою, під час яких вчитель не дотримується чітких етапів навчального процесу, традиційних видів роботи – нестандартні [2].

УРОК ЯК ОСНОВНА ФОРМА ОРГАНІЗАЦІЇ НАВЧАННЯ

Основною організаційною формою навчання в сучасній школі є урок.

Урок — форма організації навчання, за якої заняття проводить учитель з групою учнів постійного складу, одного віку й рівня підготовки впродовж певного часу й відповідно до розкладу.

Урок має такі особливості:

— є завершеною та обмеженою в часі частиною навчального процесу, під час якого розв’язуються певні навчально-виховні завдання;

— кожен урок включається в розклад і регламентується в часі та за обсягом навчального матеріалу;

— на відміну від інших форм організації навчання є постійною формою, що забезпечує систематичне засвоєння учнями знань, умінь і навичок;

— відвідування уроків обов’язкове для всіх учнів, тому вони вивчають систему знань, поділених поурочно, в певній логіці;

— є гнучкою формою організації навчання, яка дає змогу використовувати різні методи, організовувати фронтальну, групову та індивідуальну навчальну діяльність учнів;

— спільна діяльність учителя й учнів, а також спілкування великої сталої групи учнів (класу) створює можливості для згуртування колективу дітей;

— сприяє формуванню пізнавальних якостей особистості (активності, самостійності, інтересу до знань), а також розумовому розвитку учнів.

У дидактиці існує кілька підходів до класифікації уроків залежно від ознак, узятих за основу. За способами проведення виділяють уроки-лекції, уроки-бесіди, уроки-диспути, уроки самостійної роботи учнів та ін. За етапами навчальної діяльності — вступні уроки, уроки первинного ознайомлення з матеріалом, уроки формування понять, виведення законів і правил, уроки застосування знань на практиці, уроки повторення й узагальнення матеріалу, контрольні уроки, комбіновані уроки.

Найбільш вдалою в сучасній теорії та практиці навчання є класифікація, в основу якої покладено дидактичну мету і місце уроку в загальній системі уроків. Перебуваючи на однакових позиціях, ці автори пропонують різну кількість типів уроків. За класифікацією Онищука розрізняють такі типи:

1) урок засвоєння нових знань;

2) урок формування вмінь і навичок;

3) урок застосування знань, умінь і навичок;

4) урок узагальнення і систематизації знань;

5) урок перевірки, оцінювання та корекції знань, умінь і навичок;

6) комбінований урок.

Кожен тип уроку має свою структуру, тобто склад (з яких елементів або етапів складається), послідовність (в якій послідовності ці елементи входять у заняття), зв’язок (як вони пов’язані між собою).

В. Онищук увів поняття мікро- і макроструктури уроку. Макроелементи визначаються завданнями уроку певного типу. Такими, на його думку, є етапи засвоєння знань: сприймання, осмислення, узагальнення, систематизація. оскільки логіка засвоєння знань та сама, то макроструктура уроків цього типу однакова. До мікроелементів структури уроку належать засоби і способи розв’язання дидактичних завдань на кожному його етапі [4].

Час і місце, відведені на кожен структурний елемент уроку, визначаються побудовою уроку в цілому. Структура уроку повинна забезпечувати успішне розв’язання його навчально-виховних завдань, активізацію пізнавальної діяльності учнів, відповідати характерові навчального матеріалу, дидактичним і методичним засобам, які використовує вчитель. Отже, визначаючи структуру уроку, вчитель повинен враховувати тему і зміст, найдоцільніші методичні засоби і прийоми, конкретні умови, в яких проводитиметься урок, рівень підготовленості учнів тощо.

Вдосконалення уроку відбувається за такими аспектами:

а) різноманітність видів уроків (урок ділова гра, урок прес-конференція, урок - квк, урок-змагання, урок-консиліум, урок-твір, урок-винахід, урок-залік та ін.);

б) максимальна щільність уроку;

в) насиченість уроку різними видами пізнавальної діяльності;

г) запровадження самостійної діяльності в роботі учнів;

ґ) використання програмованого і проблемного навчання;

д) здійснення міжпредметних зв’язків;

е) подолання перевантаженості учнів.

Цікавими для теорії і практики є власне нестандартні уроки. Суть їх полягає в такому структуруванні змісту і форм, яке викликало б насамперед інтерес в учнів і сприяло їхньому оптимальному розвитку і вихованню. До нестандартних уроків слід віднести інтегровані, міжпредметні, театралізовані, сугестопедичні, уроки з різновіковим складом учнів та інші.

Інтегрованими називаються уроки, мета яких — подати матеріал кількох тем блоками. Міжпредметні — уроки, які ставлять за мету “спресувати” споріднений матеріал кількох предметів. Театралізовані уроки проводяться в умовах чинних програм і відведеного навчальним планом часу. Вони викликають емоції, збуджують інтерес до навчання, спираючись переважно на образне мислення, фантазію, уяву учнів. Уроки з різновіковим складом учнів мають на меті подати блоками матеріал одного предмета, що за програмою вивчається у різних класах.

Нестандартні уроки руйнують застиглі штампи так званих “зунів” (знання, уміння, навички). структура нових типів уроків також відмінна від традиційних.

 

НЕТРАДИЦІЙНИЙ УРОК «ПОДОРОЖ ДО КРАЇНИ ДРОБІВ У 6  КЛАСІ»

Мета даного уроку систематизувати знання з теми «Десяткові дроби» та «Звичайні дроби»; перевірити вміння учнів виконувати всі дії з дробами та розв’язувати задачі, що мають практичний зміст, розвивати творчі й інтелектуальні здібності учнів.

Використання дидактичних ігор допомагає розвивати інтерес до математики та почуття відповідальності.

Гра проходить у вигляді подорожі до Країни дробів. У ній беруть участь учні 6 – го класу, розбиті на команди. Кожна команда рухається за маршрутним листом, у якому вказано послідовність відвідування станцій Країни дробів.

Перелік станцій

1. Біологічна (розв’язування задач, що мають біологічний зміст).
2. Теоретична (відповіді на теоретичні запитання, що стосуються знань термінів, означень, властивостей).
3. Географічна (розв’язування задач географічного змісту).
4. Історична (відповіді на запитання з історії математики).
5. Віртуози обчислень (розв’язування прикладів на 5-6 дій на швидкість).
6. Космічна (розв’язування задач, що стосуються космічних подорожей).
7. Практична (розв’язування задач практичного змісту).
8. Логічні задачі (розв’язування задач, що мають казковий сюжет, або логічних задач).
9. Математичний лабіринт (виконання завдань лабіринту).
10. Індивідуальна (виконання кожним учнем команди тестових завдань, записаних на картках).

Командам заздалегідь було запропоноване таке домашнє завдання:

1.           Оформити математичну газету.
2.           Підготувати реферат про значення математики в різних галузях науки та сферах життя людини.
3.           Дібрати задачі з математики: практичного та історичного змісту, задачі давнини, логічні задачі.
4.           Скласти математичні кросворди.

Домашні завдання команди здають для перевірки до початку подорожі.

1. Станція «Біологічна»

1. Найменший птах на землі – колібрі, а найбільший – страус. Вага колібрі 0,18 кг, що становить 0,000002 ваги страуса. Знайти вагу страуса.

Розв’язання

0,18 кг ÷ 0,000002 = 180000 г ÷ 2 = 90000 г = 90 кг – вага страуса

2. Граничний вік горобця – 14 років, що становить або 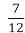віку зозулі, або 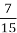віку курки, або 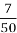віку сокола. Знайти граничний вік зозулі, курки і сокола.

Розв’язання

1.                  14 ÷ 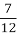= 14 × 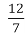= 24 (роки) – граничний вік зозулі.
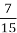2.                  14 ÷ = 14×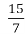 = 30 (років) – граничний вік курки.
3.                  14 ÷ 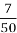= 14 × 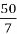=100 (років) – граничний вік сокола.

3. Граничний вік лева – 35 років, що становить 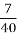граничного віку слона. Знайти граничний вік слона.

Розв’язання

35 ÷ = 35× = 200 (років) – граничний вік слона.

4. Швидкість польоту стрижа – 1600 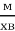, швидкість польоту шпака становить 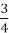, а яструба - 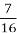швидкості польоту стрижа. Знайти швидкість польоту яструба і шпака.

Розв’язання

1.                  1600 × 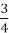= 1600 ÷ 4 × 3 = 12100  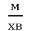() – швидкість польоту шпака.
2.             1600 × 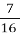= 1600 ÷ 16 × 7 = 700 (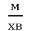) -  швидкість польоту яструба.

5. Кров становить 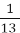маси тіла людини. 54 % всієї крові знаходиться в кровоносних судинах, 20 % - у печінці, 16 % - селезінці, 10 % - у підшкірних судинах. Скільки крові знаходиться в кровоносних судинах, печінці, селезінці та підшкірних судинах у людини масою 65 кг.

 

Розв’язання

1.     65 × 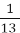= 5 (кг) – маси всієї крові.
2.     5 × 0,54 = 2,7 (кг) – крові у кровоносних судинах.
3.     5 × 0,2 = 1 (кг) – крові у печінці.
4.     5 × 0,16 = 0,8 (кг) – крові у селезінці.
5.     5 × 0,1 = 0,5 (кг) – крові у підшкірних судинах.

2. Станція «Теоретична»

Запитання для учнів

1. Який дріб називають правильним?
2. Як додати два дроби з правильними знаменниками?
3. Як порівняти два дроби з однаковими знаменниками?
4. Як порівняти дроби з одиницею?
5. Які числа називають взаємно оберненими?
6. Як виконати множення звичайних дробів?
7. Як виконати ділення звичайних дробів?
8. Яка основна властивість звичайного дробу?
9. На що вказує чисельник (знаменник) дробу?
10. Як помножити дріб на розрядну одиницю?
11. Як знайти дріб від числа?
12. Як знайти число за його дробом?
13. Як перетворити звичайний дріб у десятковий і навпаки?

 

 

3. Станція «Географічна»

1. Довжина річки Амудар’я становить 2500 км. Рівниною річка протікає 0,6 своєї довжини, а 30 % цієї ділянки – судноплавні. Визначити довжину судноплавної частини річки.

Розв’язання

1.     2500 × 0,6 = 1500 (км) – протікає річка рівниною.
2.     1500 × 0,3 = 450 (км) – становить судноплавна частина річки.

2. З 640 найважливіших культурних рослин земної кулі 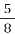походять з Азії, 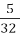- з Північної і Південної Америки, а 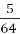- з Африки. Скільки культурних рослин походять з інших частин світу?

Розв’язання

1.     640 × 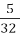= 640 ÷32 × 5 = 100 (рослин) з Північної і Південної Америки.
2.     640 × 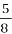= 640 ÷ 8 × 5 = 400 (рослин) з Азії.
3.     640 × 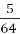= 640 ÷ 64 × 5 = 50 (рослин) з Африки.
4.     100 + 400 + 50 = 550 (рослин) з Азії, Північної і Південної Америки та Африки.
5.     640 – 550 = 90 (рослин) з інших частин світу.

3. Найбільша глибина Атлантичного океану становить 8,5 км, Тихого – на 2,3 км більша , а Північного Льодовитого – в 2 рази менша найбільшої глибини Тихого океану. Чому дорівнює найбільша глибина Північного Льодовитого океану?

Розв’язання

1.     8,5 + 2,3 = 10,8 (км) – найбільша глибина Тихого океану.
2.     10,8 ÷ 2 = 5,4 (км) – найбільша глибина Північного Льодовитого океану.

4. Висота Ключевської Сопки становить 4900 м, а висота Ельбрусу – в 1 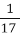раза більша, ніж висота Ключевської Сопки. Висота піка Ісмаїла Самані в 1 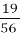раза більша, ніж висота Ельбрусу. Знайти висоту Ельбрусу та піка Ісмаїла Самані.

Розв’язання

1.     4900 × 1 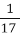= 5600 (м) - висота Ельбрусу.
2.     5600 × 1 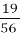= 7500 (м) - Висота піка Ісмаїла Самані.

5. Ширина Керченської протоки 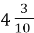км, що становить 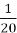ширини Берингової протоки. Яка ширина Берингової протоки?

Розв’язання

÷ = × = 86 (км) - ширини Берингової протоки.

6. Найбільшим озером земної кулі є Каспійське море. Його площа становить 424,3 тис. кв. км. Виразити площу в гектарах.

Розв’язання

424,3 тис.кв.км. = 424300 км² =424300000000 м² = 4243000 га = 4243 тис.га.

7. Площа Азовського моря приблизно дорівнює 37,8 км², що становить 0,09 площі Балтійського  моря. Визначити площу Балтійського  моря.

Розв’язання

37,8 ÷ 0,09 = 3780 ÷9 = 420 (км²) - площа Балтійського моря.

8. Довжина Суецького каналу 165,8 км, довжина Панамського каналу менша від довжини Суецького каналу на 84,7 км, а довжина Білорморсько-Балтійського каналу на 145,9 км більша від довжини Панамського. Яка довжина Білорморсько-Балтійського каналу?

Розв’язання

1. 165,8 – 84,7 = 81,1 (км) - довжина Панамського каналу.
2. 81,1 + 145,9 = 227 (км) - довжина Білорморсько-Балтійського каналу.

4. Станція «Історична».

Запитання для учнів

1. У якій роботі Ньютона вперше зустрічається поняття «дріб»?
2. Як Ньютон у «Загальній арифметиці» пояснює запис і ?
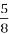3. Хто із стародавніх вчених користувався дробами?
4. Чому вавилонські дроби одержали широке розповсюдження?
5. Які вчені провели велику роботу з розвитку вчення про звичайні дроби?
6. У чому особливості запропонованого індійськими математиками запису звичайних дробів?
7. Хто вперше ввів десяткові дроби?
8. У чому полягає особливість римської системи дробів?
9. Що сказав Цицерон про значення дробів?

5. Станція «Віртуози обчислень».

Команди змагаються у правильному та швидкому виконанні дій над десятковими дробами.

1. .
2. .

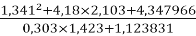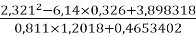6.        Станція «Космічна».

1. Довжина орбіти Місяця становить 2400000 км. Яку відстань проходить Місяць за 1 добу та за 1 год, якщо повний оберт навколо Землі він робить за 27 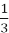доби?

Розв’язання

1.     2400000 ÷ 27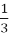= = 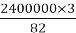87804,876 (км) – проходить Місяць за добу.
2.     87804,876 ÷ 24 = 3658,5365 (км) – проходить місяць за 1 год.

2. Відстань від Марса до Землі приблизно становить 56 млн км. За який час ракета, випущена з Землі, долетить до Марса, якщо її середня швидкість дорівнює 350 ?

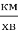Розв’язання

56000000 ÷ 350 = 160000 (хв) = 2666 (год) = 111 (діб).

3. Відстань від Землі до Місяця приблизно становить 380000 км. За скільки годин ракета, випущена з Землі, долетить до Місяця, якщо її середня швидкість дорівнює 670 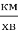на першій ділянці шляху довжиною 80000 км і 150 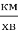на решті шляху?

Розв’язання

1.     80000 ÷ 670 = 119,4 (хв) витратить ракета на подолання першої ділянки шляху.
2.     380 000 – 80000 = 300000 (км) довжина другої ділянки шляху.
3.     300000 ÷150 = 2000 (хв) витратить ракета на подолання другої ділянки шляху.
4.     119,4 + 2000 + 2119,4 (хв) = (35,3 (год) витратить ракета на політ від Землі до Місяця.

ЕФЕКТИВНІСТЬ ЗАСТОСУВАННЯ НЕТРАДИЦІЙНИХ ФОРМ НАВЧАННЯ

Нестандартні уроки руйнують застиглі штампи так званих зунів (знання, уміння, навички). Структура нових типів уроків також відмінна від традиційних. Дидактика виходить з таких аспектів ефективності уроку. Керування пізнавальною діяльністю учнів на основі закономірностей і принципів навчання; напружена, досконало організована й результативна пізнавальна діяльність учнів; ретельна діагностика причин, що впливають на якість занять, прогнозування здійснення і результатів навчально-виховного процесу, вибір на цій основі досконалої технології досягнення запроектованих результатів; творчий підхід до розв'язання нестандартних завдань відповідно до наявних умов та можливостей; обґрунтований вибір, доцільне застосування необхідного і достатнього для досягнення мети комплексу дидактичних засобів; диференційований підхід до окремих груп учнів; ефективне використання кожної робочої хвилини на уроці; атмосфера змагання, стимулювання, дружнього спілкування, прогнозування навчальної діяльності, вибір на цій основі досконалої технології досягнень запрограмованих результатів.

Нестандартні уроки дозволяють урізноманітнювати форми й методи роботи, позбавлятися шаблонів, створюють умови для виховання творчих здібностей школяра, розширюють функції вчителя, дають змогу враховувати специфіку певного матеріалу та індивідуальні особливості кожної дитини. Використання нестандартних форм уроків сприяє формуванню пізнавальних інтересів школярів, діти безпосередньо беруть участь у процесі навчання. Пізнавальна діяльність учнів переважно має колективний характер, що створює передумови для взаємодії суб’єктів навчання, дає можливість для обміну інтелектуальними цінностями, порівняння й узгодження різних точок зору про об’єкти, які вивчаються на уроці.

Ефективність нестандартних уроків забезпечується за умови володіння вчителем методикою їх проведення та умілого використання таких уроків у певній системі в поєднанні з традиційними формами роботи.

ВИСНОВОК

В сучасних умовах важливість нестандартного уроку полягає в тому, що він підвищує ефективність навчання, зацікавлює учнів до вивчення нового матеріалу. Це зумовлює те, що у фаховій літературі, на сторінках періодичної преси, на засіданнях методичних об’єднань шкіл, на наукових конференціях ВНЗ розглядають ці важливі для теорії та практики початкової освіти питання. Сьогодні відбуваються дискусії щодо визначення сутності нестандартних уроків та цінності такої форми занять у навчанні.

Отже, в умовах зміни педагогічної парадигми нестандартний урок як своєрідне педагогічне явище бурхливо розвивається, постійно набуваючи нових рис. Він – дитя перебудови суспільства і школи, і доля його пов’язана з долею цього процесу.

Використання нестандартних уроків математики створює сприятливі умови для: організації колективної роботи різних вікових груп, що вчаться, і класів; розширення кругозору школярів за рахунок залучення їх до вивчення додаткового матеріалу з різноманітних джерел.

Таким чином, актуальність теми дослідження у сучасній системі освіти сприяла рішенню ряду завдань, поставлених на початку: навчання учнів за допомогою застосування нетрадиційних форм; розроблено методику нетрадиційних форм навчання учнів основної школи на уроках математики.

Отже, я вбачаю у використанні нетрадиційних форм і методів навчання можливість зробити процес навчання цікавим та всепоглинаючим; створити у дітей робочий настрій; допомогти подолати труднощі в засвоєнні навчального матеріалу.

Список літератури

 

1.               Про математику й математиків // Упорядники А.С. Зоря, С.М. Кіро. – К.:Рад. шк., 1981.
2.               http://ksankamach.blogspot.com/
3.               http://chekerenda.at.ua/blog/nestandartni_formi_i_metodi_roboti_na_uro kakh_matematiki_dlja_aktivizaciji_piznavalnoji_dijalnosti/2015-11-26-6
4.               http://labnit.at.ua/publ/metodichna_skrinka_vchitelja_informatiki/tipi_urokiv_po_klasifikaciji_v_a_onishhuka/4-1-0-10
5.               https://informgru.wordpress.com/
6.               Т.А. Ільїна Педагогіка. - М: - Просвіта, 1984.
7.               М. Чепіль “Педагогічні технології” - Академвидав, 2012.