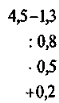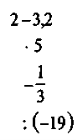Перетворення виразів. Повторення та систематизація матеріалу 5-6 класів

Тема. Перетворення виразів. Повторення та систематизація матеріалу 5-6 класів

Мета: систематизувати та узагальнити знання учнів про перетворення виразів, набуті у 5-6 класах.

Тип уроку: повторення та систематизація знань.

Хід уроку

I. Організаційний момент

Вступна бесіда.

II. Актуалізація опорних знань

На цю тему відводиться два уроки.

 Тотожні перетворення виразів є одним з найважливіших розділів шкільної алгебри.

З найпростішими перетвореннями виразів учні знайомляться вже в курсі математики 5-6 класів, де розглядаються зведення подібних доданків, винесення спільного множника за дужки; розкриття дужок, перед якими стоїть знак «+» або «-». Але оскільки більш докладно тема «Ви­рази зі змінними» буде вивчатися пізніше, на цих уроках ми акцентуємо увагу на повторенні основних способів дій під час перетворення виразів та обчисленні значень числових виразів у тому об'ємі, що є необхідним для вивчення наступної теми «Лінійне рівняння з однією змінною».

Тому на першому уроці ми розглядаємо питання «Властивості дій над числами», а на наступному — «Перетворення виразів». На уроці, присвяче­ному темі «Властивості дій над числами», бажано розглянути такі питання:

1. Алгоритми виконання дій з натуральними та раціональними числами.
2. Властивості арифметичних дій над числами.
3. Раціоналізація обчислень із використанням властивостей дій над числами.

Роботу бажано організувати так, щоб учні не просто виконали певні завдання, а щоб усвідомили алгоритми та спосіб їх застосування, а також властивості арифметичних дій та впевнилися в перевагах їх застосування для спрощення обчислень.

Слід зауважити, що треба виділити час ще на один вид роботи, дуже важливої для сприйняття матеріалу про перетворення виразів, — читання і запис числових виразів.

Окрім того, не буде зайвим нагадати учням про види чисел, які вони вивчили у 5 та 6 класах, бо вміння класифікувати математичні об'єкти є необхід­ною умовою усвідомленого використання відповідних алгоритмів. Для спро­щення роботи учнів з теоретичним матеріалом пропонуємо конспект 1 (або для фронтальної роботи, або у вигляді роздавального матеріалу на кожну парту).

III. Повторення, систематизація знань

Виконання усних вправ

2. Які властивості дій дозволяють без виконання обчислень стверджувати,
що рівності є правильними?

617 + 243 = 243 + 617; 27 · (111 + 222) = (111 + 222) · 27;

27 · (111 · 222) = (27 · 111) · 222;  27 · (111 + 222) = 27 · 111 + 27 · 222.

3. Знайдіть значення виразів і назвіть, яку властивість було використано:

25 · 3,18 · 4; 5,16 · 1,6 – 1,6 · 4,16;  6 · 2.

4. Прочитайте вирази, використовуючи слова «сума», «різниця», «добу­ток», «частка»:

2,5 + 3,7; 2,5 – 3,7; 2,5 · 3,7; 2,5 : 3,7; (2,5 + 3,7)(2,5 – 3,7).

Виконання письмових вправ

1. Використовуючи переставну та сполучну властивості дій додавання та
множення, обчисліть значення виразів найбільш раціональним способом:

1) 25 + 37 + 15 + 53; 2) 12 · 7 · 5 · 10; 3) ;

4) 1,25 · · 4 · 3;  5) 5,3 + 4,25 – 2,3 + 0,75; 6) .

2. Використовуючи розподільну властивість множення відносно додаван­ня (та віднімання), обчисліть значення виразів найбільш раціональним способом:

1) 1,64 · 5,2 + 3,36 · 5,2; 2) ; 3) ;

4) 5,32 · 4,2 – 3,32 · 4,2; 5) ; 6) .

3*. Знайдіть значення виразів:

1) ; 2) ;

3) ; 4) .

4. Запишіть числові вирази і знайдіть значення кожного з них:

1) добуток суми чисел -28 та 17 на число 1,2;

2) частка різниці чисел 12 та 4,5 і числа -1,5;

3) сума добутку чисел 11 і-12 і частки чисел 0,72 і-0,6;

4) квадрат суми чисел -5,4 та 3,8.

5*. Логічна вправа.

Встановіть, який рисунок пропущено:

(Примітка. Завдання 3* і 5* є додатковими, розв'язуються, якщо доз­волить час, бо основна мета уроку — повторення властивостей арифме­тичних дій з раціональними числами.)

IV. Рефлексія

Можливий варіант проведення цього етапу уроку — бліцтест.

Виберіть правильний (раціональний) варіант обчислень у виразі:

1) 25 + 7 + 5:   а)(25 + 7) + 5; б) (25 + 5) + 7; в) 25 + (7 + 5).

2) 25 · 7 · 4:     а) (25 · 7) · 4;   б) (25 · 4) · 7;   в) 25 · (7 · 4).

3) 3 · 3:         а) · 3;   б) 3 · 3 + · 3;   в) 3 · 3 +

V. Домашнє завдання

№ 1. Використовуючи властивості дій, обчисліть найбільш зручним способом:

1) 16 + 33 + 14 + 37; 2) 25 · 14 · 4 · 5; 3) + 3 + 1 + 1; 4) 3,2 · · 5 · 6;

5) 4,7 – 2,13 + 5,3 – 2,87;  6) 2 · 1 · 4 · 7; 7) 3,81 · 4,3 + 6,19 · 4,3;

8) ; 9) 6 · 5 + 1 · 5; 10) .

№ 2. Виконайте дії:  .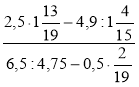

№ 3. Випереджальне домашнє завдання.

За підручником або за довідниками (див. у 6 класі) повторити види та алгоритми перетворення буквених виразів, що вивчили у 6 класі.