Розгорнутий конспект уроку: "Розв’язування вправ на повторення матеріалу 6 класу"

                                  Урок № 1                       7 клас                       

Тема.  Розв’язування вправ  на повторення матеріалу 6 класу

Мета.

• Навчальна:

• Повторення та систематизація основних понять вивчених за 6 клас
• Систематизація вмінь виконувати найпростіші арифметичні операції, вивчені у 6 класі
• Формування знань щодо предмету алгебри

• Виховна:

• Виховувати пізнавальний інтерес до математики, зацікавленість до предмету
• Сприяти вихованню  поваги  одне одного в колективі

• Розвиваюча:

• Пізнавальний та інтелектуальний розвиток учнів
• Розвиток навичок логічного мислення
• Вміння аналізувати, узагальнювати, порівнювати, робити висновки

Тривалість уроку : 45 хвилин

Тип уроку. Урок застосування знань, навичок і умінь.

Етапи уроку

1. Організаційний момент (6 хвилин)
2. Мотивація навчальної діяльності (7 хвилин)
3. Актуалізація опорних знань (10 хвилин)
4. Виконання практичних завдань (14 хвилин)
5. Підсумок уроку (6 хвилин)
6. Постановка домашнього завдання (2 хвилини)

Хід уроку

1. Організаційний момент

(Зайшовши до класу, спостерігаю за реакцією дітей.)

Добрий день, діти! (Вітаюсь, після заспокоєння учнів). Ну що, відпочили на літніх канікулах? А тепер давайте будемо налаштовуватись на рік плідного навчання, й на сьогоднішній урок. Перш за все відмітимо відсутніх.

(Перевірка наявності у дітей підручників, зошитів. Відмічення відсутніх на уроці. Підпис зошитів)

2. Мотивація навчальної діяльності

Діти, сьогодні ви розпочинаєте вивчення нового для вас предмету «Алгебра».  Можливо ви думаєте, що це щось зовсім нове і вам невідоме. Але це не так.

Вся велика математика поділяється на: арифметику - науку чисел, алгебру – науку рівнянь і нерівностей, та геометрію – науку про геометричні фігури.

Алгебра — розділ математики, що вивчає математичні операції і відношення, та утворення, що базуються на них: многочлени, алгебраїчні рівняння, алгебраїчні структури.

Алгебра як наука розв’язувати рівняння зародилася дуже давно у зв’язку з потребою знаходити різні методи розв’язувати однотипні задачі. Саме слово «алгебра» виникло після появи книги великого математика аль - Хорезмі, який став батьком і початківцем алгебри.

І ми з вами будемо розпочинати вивчати цю цікаву науку.

3. Актуалізація опорних знань

Перш за все ми повинні згадати раніше вивчений матеріал.  У 6 класі ви вивчали такі теми:

• Подільність чисел
• Звичайні дроби
• Відношення і пропорції
• Раціональні числа й дії над ними

Тому нам потрібно все це з вами повторити. Давайте розпочнемо з найпростішого.

1. Сформулюйте ознаки подільності на 2, 5, 10

(- на 2 діляться всі ті натуральні числа, запис яких закінчується парною цифрою;

- на 5 діляться всі ті натуральні числа, запис яких закінчується цифрою 0 або цифрою 5;

 - на 10 діляться всі ті натуральні числа, запис яких закінчується цифрою 0.)

2. Сформулюйте ознаки подільності на 3, 9

(- на 9 діляться всі ті натуральні числа, сума цифр яких ділиться на 9;

- на 3 діляться всі ті натуральні числа, сума цифр яких ділиться на 3.)

3. Які числа називаються простими, а які складеними?

(Натуральне число називається простим, якщо воно має тільки два різних дільники: одиницю і саме це число. Натуральне число називається складеним, якщо воно має більше двох дільників.

Наприклад, числа 2, 3, 5, 7, 11 - прості, а числа 4, 6, 15, 108 - складені. Число 1 не належить ні до простих, ні до складених.

Будь-яке складене число можна розкласти на прості множники.

Наприклад: 24 = 2 ∙ 2 ∙ 2 ∙ 3; 120 = 2 ∙ 2 ∙ 2 ∙ 3 ∙ 5; 693 = 3 ∙ 3 ∙ 7 ∙ 11.)

4. Що таке НСД і НСК? Як його знайти?

(Найбільше натуральне число, на яке ділиться число а і Ь, називається найбільшим спільним дільником (НСД) цих чисел. Щоб знайти НСД двох (або більшої кількості) чисел, треба розкласти ці числа на прості множники і знайти добуток спільних простих множників.

Найменшим спільним кратним двох натуральних чисел називають найменше натуральне число, яке ділиться на кожне з даних чисел. Щоб знайти НСК двох чисел, можна кожне з них розкласти на прості множники, і розклад одного з чисел помножити на ті множники іншого числа, яких немас в розкладі першого.)

5. Що таке звичайний дріб? (Звичайний дріб - це число у вигляді m\n, де m та n - натуральні числа; число m - чисельник, а n – знаменник дробу. )

6. Сформулюйте основну властивість дробу  (Якщо чисельник і знаменник дробу помножити або поділити на одне й те саме натуральне число, дістанемо дріб, що дорівнює даному)

7. Сформулюйте правила додавання й віднімання звичайних дробів з однаковими знаменниками (Щоб додати дроби з однаковими знаменниками, треба додати їх чисельники і суму записати в чисельник, а знаменник залишити без змін. Щоб відняти дроби з однаковими знаменниками, треба відняти їх чисельники і різницю записати у чисельник, а знаменник залишити без змін.)

8. Сформулюйте правила додавання й віднімання звичайних дробів з різними знаменниками. (Щоб додати (відняти) дроби з різними знаменниками, потрібно:

1) звести дроби до найменшого спільного знаменника;

2) додати (відняти) одержані дроби з однаковими знаменниками.)

9. Сформулюйте правило множення звичайних дробів (Щоб помножити дріб на дріб, треба:

1) знайти добуток чисельників цих дробів і добуток їх знаменників;

2) перший добуток записати чисельником, а другий - знаменником;

3) якщо можливо, скоротити дріб.)

10.                    Сформулюйте правило ділення звичайних дробів (Знаходимо обернений дріб і виконуємо правило множення звичайних дробів )

4. Виконання практичних завдань

Добре, все пригадали, молодці! А тепер спробуємо використати ваші знання на вправах і нескладних завданнях

1. Назвіть п'ять найменших натуральних чисел, які діляться на 5 (5, 10, 15, 20, 25)
2. Допишіть до числа 327 справа таку цифру, щоб утворене чотирициф­рове число ділилось на 2 і на 5. Чи ділиться воно на 10? (0, ділиться)
3. Число а ділиться на 9. Чи ділиться воно на 3? Число n ділиться на 3. Чи ділиться воно на 9? (так, ні)
4. З'ясуйте, чи правильні твердження, 15 240 ділиться:

1) на 2;  (так)

2) на 9;  (ні)

3) на 10; (так)

4) на 5;  (так)

5) є простим числом? (ні)

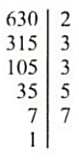
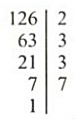5. Розкладіть числа 126 і 630 на прості множники

6. Знайдіть НСД чисел 36 і 162

162   2 36   2

   81   3 18   2

   27   3   9   3

     9   3   3   3

     3   3   1

     1

Отже НСД (162, 36) = 233 = 18

7. Запишіть числа, кратні 9, і числа, кратні 12, та підкресліть їх спільні кратні.
   число 9 кратні: 9,18, 27, 36, 45, 54, 63, 72, 81,...

число 12 кратні:   12, 24, 36, 48, 60, 72, 84, ...
Спільними кратними чисел 9 і 12 є підкреслені числа 36, 72, ... . Усі вони діляться на 9 і на 12.

Найменшим спільним кратним є число 36.

НСК(9; 12)=36

8. Знайдіть НСК двох чисел 90 і 210

Розкладаємо два числа на прості множники, і розклад одного з чисел множимо на множники другого числа, яких немає у першому розкладі

90 = 2335

210 = 2357

НСК (90; 210)  =  23357 = 630

9. Виконати дії з дробами

1.    
2.    
3.    
4.    
5.    
6.    
7.    
8.    
9.    
   1. 
   2. 
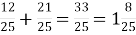
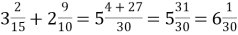
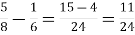
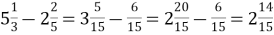
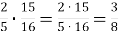
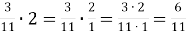
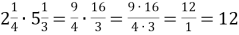
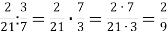
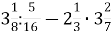
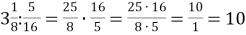
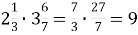
   3. 10 - 9=1

10.                    Перший оператор може набрати весь текст за 6 днів, а другий – за 12 днів. За який час оператори наберуть увесь текст, працюючи разом?

Розв’язання

Приймемо всю роботу з набору тексту за одиницю, тоді перший оператор за 1 день набере частину всього тексту, а другий - 

Працюючи разом, вони наберуть за 1 день частину тексту.

Увесь текст оператори, працюючи разом, наберуть за 1: (дні).

Відповідь. 4 дні

5. Підсумок уроку

На цьому уроці ми з вами повторили половину вивченого матеріалу  6 класу, закріпили й засвоїли знання і вміння виконувати операції над звичайними дробами.

6. Постановка домашнього завдання

Я дякую вам за увагу, активність і роботу на уроці. Запишіть будь ласка вправу в зошити, яку ви виконаєте вдома.

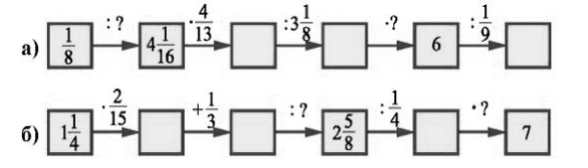
Вправа. Знайдіть пропущені числа