РОЗГАЛУЖЕНІ КОЛА ЗМІННОГО СТРУМУ Методичні вказівки для самостійної роботи при розв’язуванні задач для учнів електромонтажних професій

 

 

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

Департамент освіти і науки 

Закарпатської  обласної державної адміністрації

Тячівський професійний ліцей

 

 

 

 

РОЗГАЛУЖЕНІ КОЛА ЗМІННОГО СТРУМУ

 

Методичні вказівки

для самостійної роботи

при розв’язуванні задач

для   учнів  електромонтажних професій

 

 

 

 

 

 

Викладач методист

М.В. Принц-Цимбаліста

 

 

 

 

 

 

 

 

 

 

 

 Методичні вказівки для самостійної роботи при розв’язуванні задач з електротехніки розраховані на самостійне вивчення учнями матеріалу відповідно до робочої програми дисципліни «Електротехніка». На самостійне опрацювання виносяться питання по темі «Розгалужені кола змінного струму».

Викладач визначає обсяг і зміст самостійної роботи, узгоджує її з іншими видами навчальної діяльності, проводить поточний та підсумковий контроль, аналізує результати самостійної навчальної роботи кожного учня.

Навчальний матеріал з електротехніки, передбачений робочим

навчальним планом для засвоєння учнями в процесі самостійної роботи.

Самостійна робота учнів є одна з основних форм вивчення теоретичного

матеріалу дисципліни.

 Вивчення теоретичного матеріалу включає опрацювання навчальної, навчально-методичної та іншої літератури, програмних питань та питань, що

виносяться на аудиторні та практичні заняття.

Самостійна робота значно полегшується, якщо дотримуватися певного алгоритму при розв’язуванні задач на задану тему.

При розрахунку кола з паралельним з’єднанням споживачів необхідно визначити струми у паралельних вітках кола та визначити загальний струм.

Для такого кола, очевидно, що напруги для усіх віток  електричного кола однакові, а струм I дорівнює сумі струмів у вітках кола.

Алгоритм розрахунку наступний:

1. Визначити струми у вітках кола.

2. Кут зсуву фаз φ між струмом вітки і напругою визначають за допомогою tgφ.

3. Відповідно до першого закону Кірхгофа, струм дорівнює геометричній сумі струмів всіх віток:

Значення загального струму визначають графічно по векторної діаграмі.

4. Активна потужність кола з двома паралельними вітками дорівнює арифметичній сумі активних потужностей всіх віток

P = P₁ + P₂ .

5. Реактивна потужність електричного кола з двома паралельними вітками  дорівнює алгебраїчній сумі реактивних потужностей всіх віток,

причому реактивну потужність вітки з індуктивністю беруть зі знаком "+", вітки з ємністю - зі знаком "-".

 Наприклад

Q = Q_L1 - Q_C2 

6. Повна потужність електричного кола .

Учні в процесі самостійного вивчення теоретичного матеріалу мають

засвоїти матеріал відповідної теми, використовуючи при цьому літературні

джерела, названі в списку літератури.

Методичні вказівки  призначені для учнів професійно-технічних закладів освіти.

Розглянуто на засіданні методичної комісії

електромонтажних професій

     Протокол № 5  від 26.12. 2019.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

РОЗГАЛУЖЕНІ КОЛА ЗМІННОГО СТРУМУ

Загальні положення та основні визначення

Формули повного опору Z і зсуву фаз φ між напругою та струмом для різних випадків увімкнення активного опору R, ємності C та індуктивності L.

1. Для послідовно з’єднаних активного опору R та ємності C:

кут зсуву фаз φ визначається за формулою    .

Ємнісний опір   .

Напруга  .

Повний опір кола з активним та ємнісним опором

.

. Для послідовно з’єднаних активного опору R та індуктивності L

кут зсуву фаз φ визначається за формулою   .

Індуктивний опір .

Напруга для ділянки кола з послідовно з’єднаними активним та індуктивним опором

 .

Повний опір кола з активним та індуктивним опором

.

3. Для послідовно з’єднаних активного опору R, ємності C та індуктивності L :

кут зсуву фаз φ визначається за формулою    .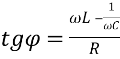

Повний опір кола з активним, індуктивним та ємнісним опором з’єднаних послідовно

, або   .

4.  Для паралельно з’єднаних активного опору R та ємності C на ділянці кола кут зсуву фаз φ визначається за формулою .

 Повний опір ділянки кола    .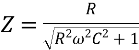

5. Для паралельно з’єднаних активного опору R та індуктивності L на ділянці кола кут зсуву фаз φ визначається за формулою   .

Повний опір ділянки кола      .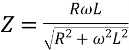

 

 

Приклади розв’язування задач

 

Задача 25. Котушка з активним опором R₁ = 6Ом та індуктивним X_L1 = 8Ом з’єднані паралельно з конденсатором, ємнісний опір якого X_С2 = 10Ом (рис. 66). Визначити: 1) струми у вітках та в нерозгалуженій частині кола; 2) кути зсуву фаз між струмом і напругою у кожній вітці і в колі вцілому; 3) активну і реактивну потужності віток і всього кола; 4) повну потужність кола. Накреслити в масштабі векторну діаграму кола. До кола прикладена напруга U =100В.

Рис. 66.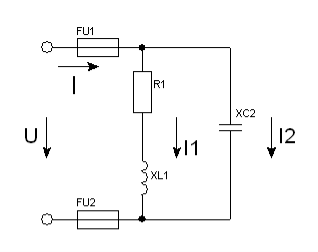

Дано: R₁ = 6Ом ; X_L1 = 8Ом ;  X_С2  = 10Ом ; U =100В (рис.66).

Знайти:  I₁ ; I₂ ;  I ; φ₁ ; φ₂ ; φ ;  P₁ ; P₂ ; P ; Q₁ ; Q₂ ; Q ;  S .

Р О З В’ Я З У В А Н Н Я.

1. Визначаємо струми у вітках:

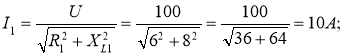
I₂ = U/X_C2 = 100/10 = 10A.

2. Кути зсуву фаз у вітках знаходимо за синусами кутів, щоб не втратити знак кута: 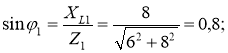      φ₁ = 53˚10΄.

Так як φ₁ > 0, тому напруга випереджує струм .

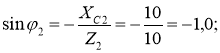         φ₂ = – 90˚, тобто напруга відстає від струму, бо φ₂ < 0. Обчислюємо значення тригонометричних функцій за допомогою калькулятора ( див. додаток). cosφ₁ = cos53˚8΄ = 0,6; cosφ₂ = 0.

3. Визначаємо активну і реактивну складові струмів у вітках:

I_А1 = I₁cosφ₁ = 10·0,6 = 6A;       I_Р1 = I₁sinφ₁ = 10·0,8 = 8A;

I_А2 = 0;                                        I_Р2 = I₂sinφ₂ = 10·(–1,0) = – 10А.

4. Визначаємо струм в нерозгалуженій частині кола:

5. Визначаємо коефіцієнт потужності всього кола:

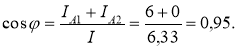
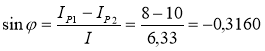; φ = – 18˚ 25΄.

6. Визначаємо активну і реактивну потужності віток і всього кола:

P₁ = U I₁ cosφ₁ =100·10·0,6 = 600Вт;

P₂ = 0;       P = P₁ + P₂ = 600Вт.

Q₁ = U I₁sinφ₁ = 100·10·0,8 = 800вар;

Q₂ = U I₂sinφ₂ = 100·10·(–1,0) = –1000вар;

Q = Q₁ + Q₂ = 800 – 1000 = – 200вар.

Реактивна потужність від’ємна, тому що має ємнісний характер, тут φ₂ < 0.

7. Визначаємо повну потужність кола:

Струм в нерозгалуженій частині кола можна визначити і за такою формулою: I = S/U = 633/100 = 6,33A .

8. Для побудови векторної діаграми вибираємо масштаб для струму: в 1см – 2,5А ; для напруги: в 1 см – 25В. Побудову починаємо з вектора напруги (рис.67). Під кутом φ₁  до нього в бік відставання відкладаємо в масштабі  вектор струму , а під кутом φ₂ в бік випередження – вектор струму . Геометрична сума цих струмів дорівнює струму в нерозгалуженій частині кола. При відсутності конденсатора реактивна потужність першої вітки не була би компенсована і струм  в колі мав би  можливість збільшитись до I = I₁ = 10А .

 

 

 Рис.67.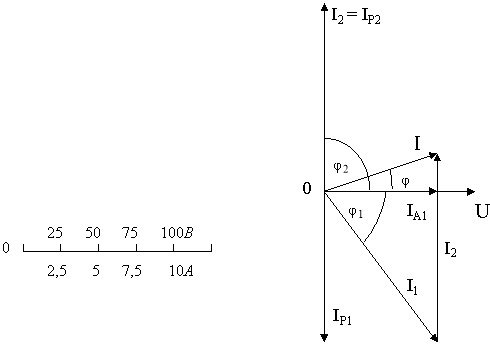 

На діаграмі показано також проекції векторів струму на вектор напруги (активна складова  ) і вектори , перпендикулярні до нього ( реактивні складові та  ).

 В І Д П О В І Д Ь. I₁ = 10A; I₂ = 10A;  I = 6,33A; φ₁ = 53˚8΄; φ₂ = – 90˚;

φ = – 18˚ 25΄;  P₁ = 600Вт;  ; P₂ = 0 ; P = 600Вт; ; Q₁ = 800вар;

 Q₂ = –1000вар; Q = – 200вар;  S = 633В·A .

Задача 26. Коло змінного струму містить різні елементи (резистори, індуктивності, ємності), які з’єднані в дві паралельні вітки. Схема кола наведена на відповідному рисунку. Номер рисунка, значення всіх опорів, а також один додатковий параметр задано нижче. Індекс „1” біля додаткового параметра означає, що він відноситься до першої вітки; індекс „2” – до другої.

Для заданого кола  визначити такі величини, якщо вони не задані в умові задачі: 1) струми I₁ та I ₂ в обох вітках; 2) струм  I  в нерозгалуженій частині кола; 3) напругу U , прикладену до кола; 4) активну  P, реактивну  Q  і повну  S потужність кола. Накреслити в масштабі векторну діаграму кола.

Рис. 68.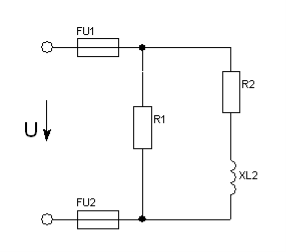 

26.1. Дано: R₁ = 2Ом ; R₂ = 3Ом ;  X_L2 = 4Ом ;  U_R2 = 12В (рис.68).

Знайти:  I₁ ; I₂ ; I ; P ; Q ; S .

Р О З В’ Я З У В А Н Н Я.

1. Визначаємо струми у вітках:

 I₂ = U_R2/R₂ = 12/3 = 4A.

При паралельному з’єднані віток   U = U₁ = U₂ ,

тут  

Тобто    U = U₁ = U₂ = 20В.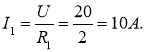          

2. Кути зсуву фаз у вітках знаходимо за синусами кутів, щоб не втратити знак кута: 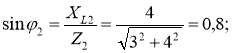      φ₂ = 53˚8΄.

Так як φ₂ > 0, тому напруга випереджує струм .

         φ₁ = 0, тобто вектор напруги співпадає з вектором струму. Обчислюємо значення тригонометричних функцій за допомогою калькулятора (див. додаток). cosφ₂ = cos53˚8΄ = 0,6;   cosφ₁ = cos0 = 1,0.

3. Визначаємо активну і реактивну складові струмів у вітках:

I_А1 = I₁cosφ₁ = 10·1,0 = 10A;       I_Р1 = I₁sinφ₁ = 10·0 = 0;

I_А2 = I₂cosφ₂ = 4·0,6 = 2,4A;        I_Р2 = I₂sinφ₂ = 4·0,8 = 3,2А.

4. Визначаємо струм в нерозгалуженій частині кола:

5. Визначаємо коефіцієнт потужності всього кола:

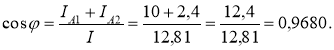
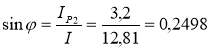; φ = 14˚ 28΄.

6. Визначаємо активну і реактивну потужності віток і всього кола:

P₁ = U I₁ cosφ₁ =20·10·1,0 = 200Вт;

P₂ = U I₂ cosφ₂ =20·4·0,6 = 48Вт;       P = P₁ + P₂ = 200 + 48 = 248Вт.

Q₁ = U I₁sinφ₁ = 20·10·0 = 0вар;

Q₂ = U I₂sinφ₂ = 20·4·0,8 = 64вар;

Q = Q₁ + Q₂ = 0 + 64 = 64вар.

Реактивна потужність додатна, тому що має індуктивний характер,

тут φ₂ > 0.

7. Визначаємо повну потужність кола:

Струм в нерозгалуженій частині кола можна визначити і за такою формулою: I = S/U = 256,125/20 = 12,806 = 12,81A .

(Неточність при обчисленні у другому знаку після коми пояснюється заокругленнями при множенні на чотиризначні величини тригонометричних функцій).

8. Для побудови векторної діаграми вибираємо масштаб для струму:

в 1см – 1А ; для напруги: в 1 см – 2,5В.

Побудову починаємо з вектора напруги (рис.68, а). Під кутом φ₁ = 0  до нього відкладаємо в масштабі  вектор струму , а під кутом φ₂ = 53˚8΄ в бік відставання – вектор струму . Геометрична сума цих струмів дорівнює струму в нерозгалуженій частині кола .

. 

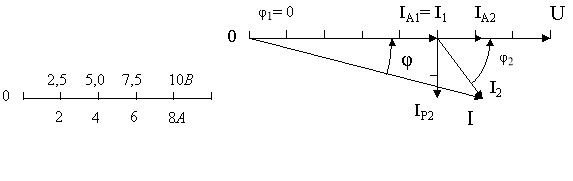
Рис.68, а

На діаграмі показано також проекції векторів струму на вектор напруги (активні складові  та ) і вектор , перпендикулярний до нього – реактивна складова .

 В І Д П О В І Д Ь.   I₁ = 10A;    I₂ = 4A;   I = 12,81A;   φ = 14˚ 28΄;

                                        P = 248Вт;  Q = 64вар;   S = 256,125В·A .

 

26.2. Дано: R₁ = 5Ом ; R₂ = 3Ом ;  X_L2 = 4Ом ;  Q = 64 вар (рис.68).

Знайти:  I₁ ; I₂ ; I ; U ;  P ; S .

26.3. Дано: R₁ = 10Ом ; R₂ = 6Ом ;  X_L2 = 8Ом ;  U = 50В (рис.68).

Знайти:  I₁ ; I₂ ; I ; P ; Q ; S .

26.4. Дано: R₁ = 4Ом ; R₂ = 4Ом ;  X_L2 = 3Ом ;  I₂ = 8А (рис.68).

Знайти:  I₁ ; I ; U ; P ; Q ; S .

26.5. Дано: R₁ = 8Ом ; R₂ = 4Ом ;  X_L2 = 3Ом ;  I₁ = 5А  (рис.68).

Знайти: I₂ ; I ; U ; P ; Q ; S .

26.6. Дано: R₁ = 8Ом ; R₂ = 4Ом ;  X_L2 = 3Ом ; P₂ = 256Вт  (рис.68).

Знайти: I₁ ; I₂ ; I ; U ; Q ; S .

26.7. Дано: R₁ = 10Ом ; R₂ = 12Ом ;  X_L2 = 8Ом ;  U_L2 = 24В (рис.68).

Знайти:  I₁ ; I₂ ; I ; P ; Q ; S .

26.8. Дано: R₁ = 5Ом ; R₂ = 16Ом ;  X_L2 = 12Ом ; P₁ = 320Вт  (рис.68).

Знайти: I₁ ; I₂ ; I ; U ; Q ; S .

26.9. Дано: R₁ = 20Ом ; R₂ = 6Ом ;  X_L2 = 8Ом ;  U = 60В (рис.68).

Знайти:  I₁ ; I₂ ; I ; P ; Q ; S .

26.10. Дано: R₁ = 10Ом ; R₂ = 12Ом ;  X_L2 = 16Ом ;  Q = 400 вар (рис.68).

Знайти:  I₁ ; I₂ ; I ; U ;  P ; S .

Задача 27. Коло змінного струму містить два резистори та ємність, які з’єднані в дві паралельні вітки. Схема кола наведена на рис. 69. Для заданого кола  визначити  величини, які не задані в умові задачі.

Рис. 69.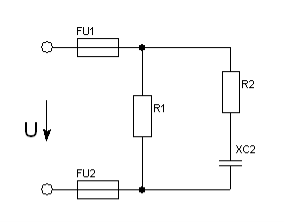

27.1. Дано: R₁ = 10Ом ; R₂ = 8Ом ;  X_С2 = 6Ом ;  U = 20В (рис.69).

Знайти:  I₁ ; I₂ ; I ; P ; Q ; S .

27.2. Дано: R₁ = 2Ом ; R₂ = 3Ом ;  X_С2 = 4Ом ;  I₁ = 5А  (рис.69).

Знайти: I₂ ; I ; U ; P ; Q ; S .

27.3. Дано: R₁ = 5Ом ; R₂ = 4Ом ;  X_С2 = 3Ом ;  I₂ = 2А  (рис.69).

Знайти: I₁ ; I ; U ; P ; Q ; S .

27.4. Дано: R₁ = 12Ом ; R₂ = 6Ом ;  X_С2 = 8Ом ;  Q =  – 288вар  (рис.69).

Знайти:  I₁ ; I₂ ; I ; U ;  P ; S .

27.5. Дано: R₁ = 3Ом ; R₂ = 3Ом ;  X_С2 = 4Ом ;  U_С2 = 12В (рис.69).

Знайти:  I₁ ; I₂ ; I ; P ; Q ; S .

27.6. Дано: R₁ = 4Ом ; R₂ = 8Ом ;  X_С2 = 6Ом ; P₁ = 100Вт  (рис.69).

Знайти: I₁ ; I₂ ; I ; U ; Q ; S .

27.7. Дано: R₁ = 8Ом ; R₂ = 16Ом ;  X_С2 = 12Ом ;  I₁ = 5А  (рис.69).

Знайти: I₂ ; I ; U ; P ; Q ; S .

27.8. Дано: R₁ = 10Ом ; R₂ = 12Ом ;  X_С2 = 16Ом ;  U _R2 = 24В (рис.69).

Знайти:  I₁ ; I₂ ; I ; P ; Q ; S .

27.9. Дано: R₁ = 4Ом ; R₂ = 8Ом ;  X_С2 = 6Ом ;  S ₂ = 40В·A (рис.69).

Знайти:  I₁ ; I₂ ; I ; U; P; Q.

27.10. Дано: R₁ = 3Ом ; R₂ = 6Ом ;  X_С2 = 8Ом ; P₂ = 54Вт  (рис.69).

Знайти: I₁ ; I₂ ; I ; U ; Q ; S .

Задача 28. Коло змінного струму містить  резистор та ємність, які з’єднані в дві паралельні вітки. Схема кола наведена на рис. 70. Для заданого кола  визначити  величини, які не задані в умові задачі.

 

Рис. 70.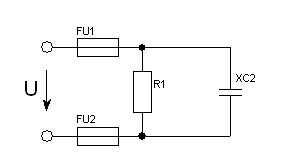

28.1. Дано: R₁ = 4Ом ; X_С2 = 5Ом ;  I₁ = 5А  (рис.70).

Знайти: I₂ ; I ; U ; P ; Q ; S .

28.2. Дано: R₁ = 12Ом ; X_С2 = 8Ом ;  I₂ = 6А  (рис.70).

Знайти: I₁ ; I ; U ; P ; Q ; S .

28.3. Дано: R₁ = 2Ом ; X_С2 = 4Ом ;  U = 8В (рис.70).

Знайти:  I₁ ; I₂ ; I ; P ; Q ; S .

28.4. Дано: R₁ = 3Ом ; X_С2 = 4Ом ; P = 48Вт  (рис.70).

Знайти: I₁ ; I₂ ; I ; U ; Q ; S .

28.5. Дано: R₁ = 5Ом ; X_С2 = 10Ом ;  Q =  – 40вар  (рис.70).

Знайти:  I₁ ; I₂ ; I ; U ;  P ; S .

28.6. Дано: R₁ = 6Ом ; X_С2 = 3Ом ;  I₁ = 2А  (рис.70).

Знайти: I₂ ; I ; U ; P ; Q ; S .

28.7. Дано: R₁ = 4Ом ; X_С2 = 6Ом ;  U = 12В (рис.70).

Знайти:  I₁ ; I₂ ; I ; P ; Q ; S .

28.8. Дано: R₁ = 5Ом ; X_С2 = 8Ом ; P = 125Вт  (рис.70).

Знайти: I₁ ; I₂ ; I ; U ; Q ; S .

28.9. Дано: R₁ = 8Ом ; X_С2 = 6Ом ;  I₁ = 8А  (рис.70).

Знайти: I₂ ; I ; U ; P ; Q ; S .

28.10. Дано: R₁ = 6Ом ; X_С2 = 8Ом ;  I₁ = 5А  (рис.70).

Знайти: I₂ ; I ; U ; P ; Q ; S .

Задача 29. Коло змінного струму містить два резистори та дві індуктивності, які з’єднані в дві паралельні вітки. Схема кола наведена на рис.69. Для заданого кола  визначити  величини, які не задані в умові задачі.

 

Рис. 71.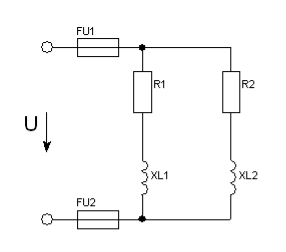

29.1. Дано: R₁ = 4Ом ; R₂ = 6Ом ; X_L1 = 3Ом ; X_L2 = 8Ом ;  I₂ = 4А  (рис.71).

Знайти: I₁ ; I ; U ; P ; Q ; S .

29.2. Дано: R₁ = 6Ом; R₂ = 3Ом; X_L1 = 8Ом ; X_L2 = 4Ом ; P₂ = 54Вт  (рис.71).

Знайти: I₁ ; I₂ ; I ; U ; Q ; S .

29.3. Дано:R₁ =8Ом; R₂ = 12Ом; X_L1 = 6Ом; X_L2 =16Ом; Q = 144вар  (рис.71).

Знайти:  I₁ ; I₂ ; I ; U ;  P ; S .

29.4. Дано: R₁ = 16Ом ; R₂ = 3Ом; X_L1 = 12Ом; X_L2 = 4Ом;  U = 40В (рис.71).

Знайти:  I₁ ; I₂ ; I ; P ; Q ; S .

29.5. Дано: R₁ = 24Ом; R₂ =12Ом; X_L1 =32Ом; X_L2 =16Ом; U_R1 =48В (рис.71).

Знайти:  I₁ ; I₂ ; I ; P ; Q ; S .

29.6. Дано: R₁ = 16Ом; R₂ = 32Ом; X_L1 = 12Ом; X_L2 = 24Ом;

 U_L1 = 48В (рис.71).

Знайти:  I₁ ; I₂ ; I ; P ; Q ; S .

29.7. Дано: R₁ = 32Ом; R₂ = 12Ом; X_L1 = 24Ом; X_L2 = 16Ом;

Q_L2 = 64вар  (рис.71).

Знайти:  I₁ ; I₂ ; I ; U ;  P ; S .

29.8. Дано: R₁ = 64Ом; R₂ = 24Ом; X_L1 = 48Ом ; X_L2 = 32Ом ;

 P₁ = 576Вт  (рис.71).

Знайти: I₁ ; I₂ ; I ; U ; Q ; S .

29.9. Дано: R₁ = 24Ом; R₂ = 16Ом; X_L1 = 32Ом ; X_L2 = 12Ом ;

P₂ = 256Вт  (рис.71).

Знайти: I₁ ; I₂ ; I ; U ; Q ; S .

29.10. Дано: R₁ = 48Ом; R₂ = 32Ом; X_L1 = 64Ом; X_L2 = 24Ом;

 Q₂ = 96вар  (рис.71).

Знайти:  I₁ ; I₂ ; I ; U ;  P ; S.

Задача 30. Коло змінного струму містить різні елементи (резистор, індуктивність, ємність), які з’єднані в дві паралельні вітки. Схема кола наведена на рис.72. Для заданого кола  визначити  величини, які не задані в умові задачі.

 

Рис. 72.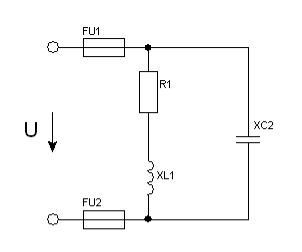

30.1. Дано: R₁ = 16Ом; X_L1 = 12Ом ; X_С2 = 10Ом ; P = 256Вт  (рис.72).

Знайти: I₁ ; I₂ ; I ; U ; Q ; S .

Р О З В’ Я З У В А Н Н Я.

1. Визначаємо опори Z₁ та Z₂  кожної вітки:

Z₂ = X_C2 = 10Ом.

2. Кути зсуву фаз у вітках кола визначаємо за синусами кутів, щоб не втратити знак кута 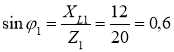   ;  φ₁ = arcsin0,6 =  36˚ 52΄,

необхідно врахувати, що φ₁ > 0, а це значить, що напруга випереджує струм. 

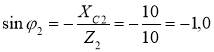  ;  φ₂ = arcsin( – 1) = – 90˚ ,

φ₂ < 0, а це значить, що напруга відстає від струму .

cosφ₁ = cos36˚ 52΄ = 0,8;    cosφ₂ = cos(– 90˚ ) = 0;

3. Якщо дано P = 256Вт, P = P₁ + P₂ ,але P₂ = 0, тоді P₁ = P = 256Вт

 із формул I₁ = P₁/(U₁ соsφ₁) ;

                  I₁ = U₁/Z₁ ,      маємо:

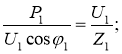  тоді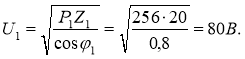      

U = U₁ = U₂= 80B,   бо вітки кола з’єднані паралельно.

4. Визначаємо струми у вітках:

 I₁ = U/Z₁ = 80/20 = 4А;   

I₂ = U/Z₂ = 80/10 = 8А.

5. Визначаємо активні та реактивні складові струмів у вітках:

I_А1 = I₁cosφ₁ = 4·0,8 = 3,2A;             I_Р1 = I₁sinφ₁ = 4·0,6 = 2,4A;

I_А2 = I₂cosφ₂ = 8·0 = 0;                     I_Р2 = I₂sinφ₂ = 8·(– 1,0) = – 8А.

6. Визначаємо струм в нерозгалуженій частині кола:

       7. Визначаємо коефіцієнт потужності всього кола:

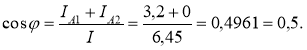
8. Визначаємо активну і реактивну потужності віток і всього кола:

P₁ = U I₁ cosφ₁ = 80·4·0,8 = 256Вт;

P₂ = U I₂ cosφ₂ = 80·8·0 = 0; 

P = P₁ + P₂ = 256 + 0  = 256Вт.

Q₁ = U I₁sinφ₁ = 80·4·0,6 = 192вар;

Q₂ = U I₂sinφ₂ = 80·8·(– 1,0) = – 640вар;

Q = Q₁ + Q₂ = 192 + ( – 640) = – 448вар.

Реактивна потужність від’ємна, тому що має ємнісний характер.

9. Визначаємо повну потужність кола:

S = 515,98 = 516A .

10. Для побудови векторної діаграми  (рис.72, а)  вибираємо масштаб:

для струму в 1см – 1А ; для напруги в 1 см – 10В.

Побудову починаємо з вектора напруги .

До нього в бік відставання по фазі, під кутом φ₁ = 36˚52΄,   відкладаємо в масштабі вектор струму ,  а в бік випередження по фазі до вектора напруги під кутом φ₂ = – 90˚  відкладаємо в масштабі вектор струму . Геометрична сума цих струмів дорівнює струму в нерозгалуженій частині кола.

Рис. 72, а.

На діаграмі показано також проекції векторів струму на вектор напруги (активна складова  ) і вектор , перпендикулярний до нього (реактивні складові та  ).

 

30.2. Дано: R₁ = 32Ом ; X_L1 = 24Ом; X_С2 = 40Ом;  U = 120В (рис.72).

Знайти:  I₁ ; I₂ ; I ; P ; Q ; S .

30.3. Дано: R₁ = 48Ом; X_L1 = 32Ом; X_С2 = 60Ом; U_R1 = 144В (рис.72).

Знайти:  I₁ ; I₂ ; I ; P ; Q ; S .

30.4. Дано: R₁ = 8Ом; X_L1 = 6Ом; X_С2 = 8Ом; U_L1 = 32В (рис.72).

Знайти:  I₁ ; I₂ ; I ; P ; Q ; S .

30.5. Дано: R₁ = 6Ом; X_L1 = 8Ом; X_С2 = 12Ом; Q _L1 = 288вар (рис.72).

Знайти:  I₁ ; I₂ ; I ; U; P ; S .

30.6. Дано: R₁ = 32Ом; X_L1 = 24Ом ; X_С2 = 25Ом ; P = 800Вт  (рис.72).

Знайти: I₁ ; I₂ ; I ; U ; Q ; S .

30.7. Дано: R₁ = 12Ом ; X_L1 = 16Ом ; X_С2 = 15Ом ;  I₂ = 4А  (рис.72).

Знайти: I₁ ; I ; U ; P ; Q ; S .

30.8. Дано: R₁ = 8Ом; X_L1 = 6Ом; X_С2 = 5Ом; Q _С2 = – 80вар (рис.72).

Знайти:  I₁ ; I₂ ; I ; U; P ; S .

30.9. Дано: R₁ =  6Ом ; X_L1 =  8Ом ; X_С2 = 10Ом ;  I₂ = 2А  (рис.72).

Знайти: I₁ ; I ; U ; P ; Q ; S .

30.10. Дано: R₁ = 3Ом ; X_L1 = 4Ом; X_С2 = 5Ом;  U = 40В (рис.72).

Знайти:  I₁ ; I₂ ; I ; P ; Q ; S .

Задача 31. Коло змінного струму містить різні елементи (резистори, індуктивність, ємність), які з’єднані в дві паралельні вітки. Схема кола наведена на рис.73. Для заданого кола  визначити  величини, які не задані в умові задачі.

 

Рис. 73.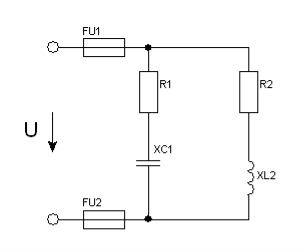

31.1. Дано: R₁ = 12Ом; R₂ = 8Ом;  X_L2 = 10Ом; X_С1 = 16Ом;

 Q _L2 = 250вар (рис.73).

Знайти:  I₁ ; I₂ ; I ; U; P ; S .

Р О З В’ Я З У В А Н Н Я.

1. Визначаємо опори Z₁ та Z₂  кожної вітки:

2. Кути зсуву фаз у вітках кола визначаємо за синусами кутів, щоб не втратити знак кута 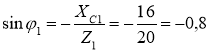   ;  φ₁ = arcsin(– 0,8)= – 53˚ 8΄,

необхідно врахувати, що φ₁ < 0, а це значить, що напруга відстає від струму;

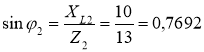  ;  φ₂ = arcsin0,7692 =  50˚ 17΄,

φ₂ > 0, а це значить, що напруга випереджує струм.

cosφ₁ = cos(–53˚ 8΄) = 0,6;    cosφ₂ = cos(50˚ 17΄) = 0,639;

3. Якщо дано  Q _L2 = 250вар, тоді із формули Q _L2 = I₂Usinφ₂ маємо:

I₂ = Q _L2/Usinφ₂ , або I₂ = U/Z₂    звідси випливає Q _L2/Usinφ₂  = U/Z₂ , або

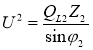,     тобто    .

4. Визначаємо струми у вітках:

 I₁ = U/Z₁ = 64,5/20 = 3,23 = 3,2А;   

I₂ = U/Z₂ = 64,5/13 = 4,96 = 5А.

5. Визначаємо активні та реактивні складові струмів у вітках:

I_А1 = I₁cosφ₁ = 3,2·0,6 = 1,92A = 2A ;  I_Р1 = I₁sinφ₁ = 3,2·(– 0,8) = – 2,6A;

I_А2 = I₂cosφ₂ = 5·0,639 = 3,2А;                     I_Р2 = I₂sinφ₂ = 5·0,7692 = 3,85А.

6. Визначаємо струм в нерозгалуженій частині кола:

7. Визначаємо коефіцієнт потужності всього кола:

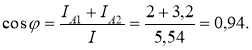
8. Визначаємо активну і реактивну потужності віток і всього кола:

P₁ = U I₁ cosφ₁ =64,5·3,2·0,6 = 123,8Вт;

P₂ = U I₂ cosφ₂ =64,5·5·0,639 = 206,1Вт ; 

P = P₁ + P₂ = 123,8Вт +206,1Вт  = 329,9Вт.

Q₁ = U I₁sinφ₁ = 64,5·3,2·(–0,8) = – 165,12вар;

Q₂ = U I₂sinφ₂ = 64,5·5·0,7692 = 248,07вар;

Q = Q₁ + Q₂ = – 165,12 + 248,07 = 82,95вар.

Реактивна потужність додатна, тому що має індуктивний характер.

9. Визначаємо повну потужність кола:

10. Для побудови векторної діаграми  (рис.73, а)  вибираємо масштаб:

для струму в 1см – 1А ; для напруги в 1 см – 10В.

Побудову починаємо з вектора напруги .

До нього в бік випередження по фазі, під кутом φ₁ = – 53˚ 8΄,   відкладаємо в масштабі вектор струму ,  а в бік відставання по фазі до вектора напруги під кутом φ₂ = 50˚ 17΄ відкладаємо в масштабі вектор струму . Геометрична сума цих струмів дорівнює струму в нерозгалуженій частині кола.

 

 

 Рис. 73, а.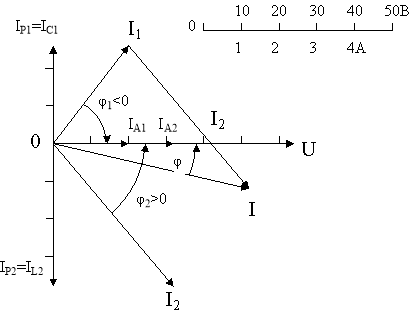 

На діаграмі показано також проекції векторів струму на вектор напруги (активні складові  ;) і вектори, перпендикулярні до нього (реактивні складові та  ).

 В заданому розгалуженому колі (рис.73) резонанс струмів може бути при умові, що опори  X_C1 = X_L2.

 

В І Д П О В І Д Ь. I₁ = 3,2А; I₂ = 5А; I = 5,35А ; U = 64,5В ; P = 329,9Вт;

 S = 340,17В·А.

31.2. Дано: R₁ = 24Ом ; R₂ = 16Ом; X_L2 = 12Ом; X_С1 = 32Ом;

 U = 80В (рис.73).

Знайти:  I₁ ; I₂ ; I ; P ; Q ; S .

31.3. Дано: R₁ = 3Ом; R₂ = 8Ом;  X_L2 = 6Ом; X_С1 = 4Ом;  I₁ = 5А  (рис.73).

Знайти: I₂ ; I ; U ; P ; Q ; S .

31.4. Дано: R₁ = 32Ом; R₂ = 16Ом;  X_L2 = 12Ом; X_С1 = 24Ом;  

I₂ = 6А  (рис.73).

Знайти: I₁ ; I ; U ; P ; Q ; S .

31.5. Дано: R₁ = 4Ом; R₂ = 6Ом;  X_L2 = 8Ом; X_С1 = 3Ом;

 P₁ = 256Вт  (рис.73).

Знайти: I₁ ; I₂ ; I ; U ; Q ; S .

31.6. Дано: R₁ = 8Ом; R₂ = 6Ом;  X_L2 = 8Ом; X_С1 = 6Ом;

 Q _С2 = – 150вар (рис.73).

Знайти:  I₁ ; I₂ ; I ; U; P ; S .

31.7. Дано: R₁ = 64Ом; R₂ = 24Ом;  X_L2 = 32Ом; X_С1 = 48Ом;

S₂ = 640В·A (рис.73).

Знайти:  I₁ ; I₂ ; I ; U; P; Q.

31.8. Дано: R₁ = 3Ом; R₂ = 4Ом;  X_L2 = 3Ом; X_С1 = 4Ом; U_R2 = 16В (рис.73).

Знайти:  I₁ ; I₂ ; I ; P ; Q ; S .

31.9. Дано: R₁ = 16Ом; R₂ = 32Ом;  X_L2 = 24Ом; X_С1 = 12Ом;

S₁ = 720В·A (рис.73).

Знайти:  I₁ ; I₂ ; I ; U; P; Q.

31.10. Дано: R₁ = 8Ом ; R₂ = 3Ом; X_L2 = 4Ом; X_С1 = 6Ом;  U_С1 = 30В (рис.73).

Знайти:  I₁ ; I₂ ; I ; P ; Q ; S .

Задача 32. Коло змінного струму містить різні елементи (резистори, індуктивність), які з’єднані в дві паралельні вітки. Схема кола наведена на рис.74. Для заданого кола  визначити  величини, які не задані в умові задачі.

 

Рис. 74.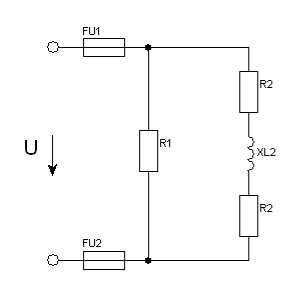

32.1. Дано: R₁ = 5Ом ; R₂ = 2Ом; X_L2 = 3Ом; U = 20В (рис.74).

Знайти:  I₁ ; I₂ ; I ; P ; Q ; S .

Р О З В’ Я З У В А Н Н Я.

1.  При паралельному з’єднані віток   U = U₁ = U₂ = 20В.

Визначаємо струми у вітках: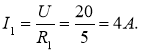

 

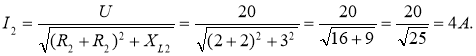
2. Кути зсуву фаз у вітках знаходимо за синусами кутів, щоб не втратити знак кута:  

         φ₁ = 0, тобто вектор напруги співпадає з вектором струму. 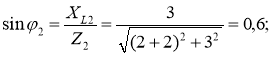    φ₂ = 36˚52΄.

Так як φ₂ > 0, тому напруга випереджує струм .

Обчислюємо значення тригонометричних функцій за допомогою калькулятора (див. додаток).     cosφ₁ = cos0  = 1,0;    cosφ₂ = cos36˚52΄ = 0,8.

3. Визначаємо активну і реактивну складові струмів у вітках:

I_А1 = I₁cosφ₁ = 4·1,0 = 4A;       I_Р1 = I₁sinφ₁ = 4·0 = 0;

I_А2 = I₂cosφ₂ = 4·0,8 = 3,2A;        I_Р2 = I₂sinφ₂ = 4·0,6 = 2,4А.

4. Визначаємо струм в нерозгалуженій частині кола:

5. Визначаємо коефіцієнт потужності всього кола:

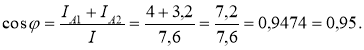
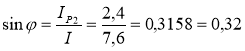; φ = 18˚ 25΄= 18˚.

6. Визначаємо активну і реактивну потужності віток і всього кола:

P₁ = U I₁ cosφ₁ =20·4·1,0 = 80Вт;

P₂ = U I₂ cosφ₂ =20·4·0,8 = 64Вт;       P = P₁ + P₂ = 80 + 64 = 144Вт.

Q₁ = U I₁sinφ₁ = 20·4·0 = 0вар;

Q₂ = U I₂sinφ₂ = 20·4·0,6 = 48вар;

Q = Q₁ + Q₂ = 0 + 48 = 48вар.

Реактивна потужність додатна, тому що має індуктивний характер,

тут φ₂ > 0.

7. Визначаємо повну потужність кола:

Струм в нерозгалуженій частині кола можна визначити і за такою формулою: I = S/U = 151,789/20 = 7,589 = 7,6A .

8. Для побудови векторної діаграми вибираємо масштаб для струму:

в 1см – 1А ; для напруги: в 1 см – 2,5В.

Побудову починаємо з вектора напруги (рис.74, а). Під кутом φ₁ = 0  до нього відкладаємо в масштабі  вектор струму , а під кутом φ₂ = 36˚52΄ в бік відставання – вектор струму . Геометрична сума цих струмів дорівнює струму в нерозгалуженій частині кола .

. 

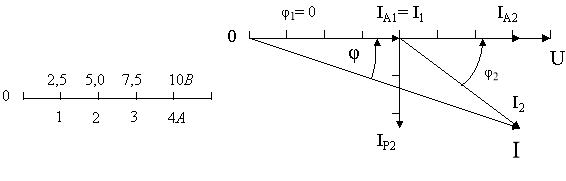
Рис.74, а

На діаграмі показано також проекції векторів струму на вектор напруги (активні складові  та ) і вектор , перпендикулярний до нього – реактивна складова .

 В І Д П О В І Д Ь.   I₁ = 10A;    I₂ = 4A;   I = 12,81A;   φ = 14˚ 28΄;

                                        P = 248Вт;  Q = 64вар;   S = 256,125В·A .

 

 

32.2. Дано: R₁ = 2Ом ; R₂ = 2Ом; X_L2 = 3Ом; P₂ = 16Вт  (рис.74).

Знайти: I₁ ; I₂ ; I ; U ; Q ; S .

32.3. Дано: R₁ = 6Ом ; R₂ = 3Ом; X_L2 = 8Ом; Q  = 72вар (рис.74).

Знайти:  I₁ ; I₂ ; I ; U; P ; S .

32.4. Дано: R₁ = 5Ом ; R₂ = 4Ом; X_L2 = 6Ом; I₂ = 6А  (рис.74).

Знайти: I₁ ; I ; U ; P ; Q ; S .

32.5. Дано: R₁ = 9Ом ; R₂ = 4Ом; X_L2 = 6Ом; I₁ = 10А  (рис.74).

Знайти: I₂ ; I ; U ; P ; Q ; S .

32.6. Дано: R₁ = 15Ом ; R₂ = 8Ом; X_L2 = 12Ом; S₂ = 180В·A (рис.74).

Знайти:  I₁ ; I₂ ; I ; U; P; Q.

32.7. Дано: R₁ = 6Ом ; R₂ = 4Ом; X_L2 = 6Ом; U_R2 = 12В (рис.74).

Знайти:  I₁ ; I₂ ; I ; P ; Q ; S .

32.8. Дано: R₁ = 20Ом ; R₂ = 16Ом; X_L2 = 24Ом; P₁ = 320Вт  (рис.74).

Знайти: I₁ ; I₂ ; I ; U ; Q ; S .

32.9. Дано: R₁ = 5Ом ; R₂ = 3Ом; X_L2 = 8Ом; U_L2 = 12В (рис.74).

Знайти:  I₁ ; I₂ ; I ; P ; Q ; S.

32.10. Дано: R₁ = 12Ом ; R₂ = 6Ом; X_L2 = 16Ом; U = 60В (рис.74).

Знайти:  I₁ ; I₂ ; I ; P ; Q ; S.

Задача 33. Коло змінного струму містить різні елементи (резистори, індуктивність, ємність), які з’єднані в дві паралельні вітки. Схема кола наведена на рис.75. Для заданого кола  визначити  величини, які не задані в умові задачі.

 

Рис. 75.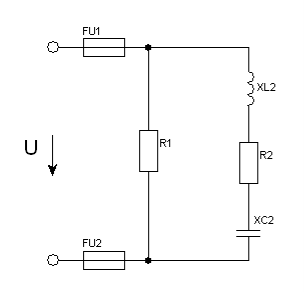

33.1. Дано: R₁ = 16Ом; R₂ = 16Ом; X_L2 = 8Ом; X_С2 = 20Ом;

 Q _L2 = 128вар (рис.75).

Знайти:  I₁ ; I₂ ; I ; U; P ; S .

Р О З В’ Я З У В А Н Н Я.

1. Для визначення струму в другій вітці використаємо формулу:

 Q_L2 = U_L2· I₂ , враховуючи, що U_L2 = I₂ X_L2 , дістанемо  Q_L2 = I₂²X_L2 .

Звідси випливає: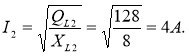

2. Визначаємо спад напруги на опорах другої вітки:

U_R2 = I₂ R₂ = 4·16 = 64 В.   U_L2 = I₂ X_L2 = 4·8 = 32 В.   U_C2 = I₂ X_C2 = 4·20 = 80 В.

3. Обчислюємо спад напруги у другій вітці:

4. Для паралельного з'єднання віток маємо:

U =  U₁ =  U₂ = 80В.

5. Струм у першій вітці   I₁= U₁/ R₁ = 80/16 = 5А.

6. Визначаємо струм в нерозгалуженій ділянці кола за формулою:

, 

 де І_А1 = І₁ = 5А ;    І_Р1 = 0.     І_А2 = І₂cosφ₂ ;   І_Р2 = І₂sinφ₂ .

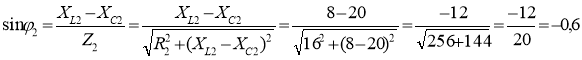
φ₂ = arcsin(–0,6) = –36˚52΄.

cosφ₂ = cos(–36˚52΄) = 0,8;

таким чином      І_А2 = І₂cosφ₂ = 4·0,8 = 3,2А;  

                            І_Р2 = І₂sinφ₂  = 4·(– 0,6) = – 2,4А.

7. Визначаємо коефіцієнт потужності кола

sinφ = І_Р2/І = (– 2,4А)/8,51А = – 0,2820;

φ = arcsin(– 0,2820) = –16˚23΄.

8. Визначаємо активну  P, реактивну  Q  і повну  S потужність кола.

 P₁ = UІ₁cosφ₁ = UІ₁·1,0 = 80 ·5 = 400Вт;

 P₂ = UІ₂cosφ₂ = UІ₂·0,8 = 80 ·4·0,8 = 256Вт;

 P = P₁ + P₂ = 400 +256 = 656Вт.

Q₁ = UІ₁ sinφ₁  = 80·5·0 = 0;

Q₂ = UІ₂ sinφ₂  = 80·4·(–0,6)  = – 192вар;

Q = Q₁ + Q₂ = 0 – 192 = – 192вар;

9. Струм в нерозгалуженій частині можна визначити значно простіше, не розкладаючи струми на складові, якщо відомо повну потужність кола і напругу:

I = S/U = 681/80= 8,51A .

10. Для побудови векторної діаграми вибираємо масштаб для струму: 

в1см – 1А;   для напруги: в 1см – 10В. (Рис. 75, а).

Побудову починаємо з вектора напруги , його довжина

80В/(10В/см) = 8см.

Вектор струму співпадає з вектором напруги , і його довжина буде

5А/(1А/см) = 5см. Під кутом φ₂ ( в бік випередження ) – вектор струму довжиною 4А/(1А/см) = 4см. Геометрична сума цих векторів дорівнює струму в нерозгалуженій частині кола. Струм в нерозгалуженій частині кола випереджує напругу на кут φ = – 16˚23΄.

 Рис.75, а.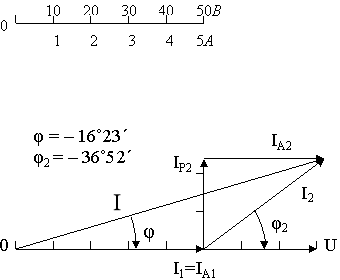 

На діаграмі показано також проекції векторів струму на вектор напруги ( активні складові  ) і вектор , перпендикулярний до нього ( реактивна складова  ).

33.2. Дано: R₁ = 5Ом; R₂ = 8Ом;  X_L2 = 4Ом; X_С2 = 10Ом; U = 30В (рис.75).

Знайти:  I₁ ; I₂ ; I ; P ; Q ; S.

33.3. Дано: R₁ = 10Ом; R₂ = 6Ом; X_L2 = 12Ом; X_С2 = 4Ом; Q = 32вар (рис.75).

Знайти:  I₁ ; I₂ ; I ; U; P ; S .

33.4. Дано: R₁ = 20Ом; R₂ = 32Ом; X_L2 = 30Ом; X_С2 = 6Ом;

 P₂ = 128Вт  (рис.75).

Знайти: I₁ ; I₂ ; I ; U ; Q ; S .

33.5. Дано: R₁ = 5Ом; R₂ = 8Ом; X_L2 = 4Ом; X_С2 = 10Ом;

 Q _С2 = – 640вар (рис.75).

Знайти:  I₁ ; I₂ ; I ; U; P ; S .

33.6. Дано: R₁ = 20Ом; R₂ = 24Ом; X_L2 = 40Ом; X_С2 = 8Ом;

 U_R2 = 24В (рис.75).

Знайти:  I₁ ; I₂ ; I ; P ; Q ; S .

33.7. Дано: R₁ = 15Ом; R₂ = 12Ом;  X_L2 = 20Ом; X_С2 = 4Ом;

P₁ = 240Вт  (рис.75).

Знайти: I₁ ; I₂ ; I ; U ; Q ; S .

33.8. Дано: R₁ = 10Ом; R₂ = 3Ом; X_L2 = 8Ом; X_С2 = 4Ом;

 S₂ = 500В·A (рис.75).

Знайти:  I₁ ; I₂ ; I ; U; P; Q.

33.9. Дано: R₁ = 60Ом; R₂ = 24Ом; X_L2 = 12Ом; X_С2 = 60Ом;

 U_L2 = 36В (рис.75).

Знайти:  I₁ ; I₂ ; I ; P ; Q ; S .

33.10. Дано: R₁ = 2Ом; R₂ = 4Ом; X_L2 = 7Ом; X_С2 = 4Ом; U_С2 = 16В (рис.75).

Знайти:  I₁ ; I₂ ; I ; P ; Q ; S .

Задача 34. Коло змінного струму містить різні елементи (резистори, ємності), які з’єднані в дві паралельні вітки. Схема кола наведена на рис.76. Для заданого кола  визначити  величини, які не задані в умові задачі.

 

Рис. 76.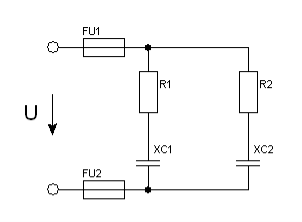

34.1. Дано: R₁ = 6Ом; R₂ = 12Ом; X_С1 = 8Ом; X_С2 = 16Ом; U_С1 = 16В (рис.76).

Знайти:  I₁ ; I₂ ; I ; P ; Q ; S .

Р О З В’ Я З У В А Н Н Я.

1.Опір кожної вітки кола:

.

.

2. Струми та напруги у вітках кола:

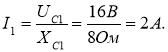                         U₁=I₁·Z₁ = 2A ·10Ом = 20В.

Вітки з’єднані паралельно, тому      U₁ = U₂ = U = 20B.

             

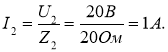
3. Кути зсуву фаз у вітках визначаємо за синусами кутів, щоб не втратити знак кута:

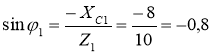;  φ₁= – 53˚ 8΄, тобто вектор напруги  по фазі відстає від вектора струму , бо φ₁ < 0; cosφ₁ = cos(–53˚ 8΄) = 0,6.

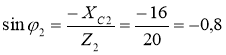;  φ₂= – 53˚ 8΄, тобто вектор напруги  по фазі відстає від вектора струму , бо φ₂ < 0; cosφ₂ = cos(–53˚ 8΄) = 0,6.

4. Активні та реактивні складові струмів у паралельних вітках кола:

І_А1 = І₁cosφ₁ = 2·0,6 = 1,2А;                 І_Р1 = І₁sinφ₁  = 2·(– 0,8) = – 1,6А.

І_А2 = І₂cosφ₂ = 1·0,6 = 0,6А;                 І_Р2 = І₂sinφ₂  = 1·(– 0,8) = – 0,8А.

5. Струм в нерозгалуженій частині кола:

6. Коефіцієнт потужності всього кола  

sinφ = (І_Р1 + І_Р2)/І = (–1,6 – 0,8)А/3А = – 0,8;

7. Визначаємо активну  P, реактивну  Q  і повну  S потужність кола.

 P₁ = UІ₁cosφ₁ = UІ₁·0,6 = 20 ·2·0,6  = 24Вт;

 P₂ = UІ₂cosφ₂ = UІ₂·0,6 = 20 ·1·0,6 = 12Вт;

 P = P₁ + P₂ = 24 +12 = 36Вт.

Q₁ = UІ₁ sinφ₁  = 20·2·(–0,8)   = – 32вар;

Q₂ = UІ₂ sinφ₂  = 20·1·(–0,8)  = – 16вар;

Q = Q₁ + Q₂ = – 32вар  – 16вар = – 48вар;

8. Для побудови векторної діаграми вибираємо масштаб для струму: 

в1см – 0,5А;   для напруги: в 1см – 5В. (Рис. 76, а).

Побудову починаємо з вектора напруги , його довжина

20В/(5В/см) = 8см.

До нього в бік випередження по фазі, під кутом φ₁ = – 53˚ 8΄,   відкладаємо в масштабі вектор струму ,  і в бік випередження по фазі до вектора напруги під кутом φ₂ = – 53˚ 8΄ відкладаємо в масштабі вектор струму . Геометрична сума цих струмів дорівнює струму в нерозгалуженій частині кола.

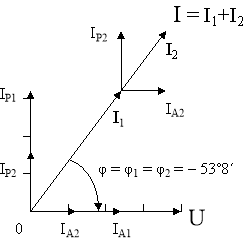Рис. 76, а.

На діаграмі показано також проекції векторів струму на вектор напруги  (активні складові  ;) і вектори , перпендикулярні до нього ( реактивні складові та  ).

 

34.2. Дано: R₁ = 8Ом; R₂ = 16Ом; X_С1 = 6Ом; X_С2 = 12Ом; U = 100В (рис.76).

Знайти:  I₁ ; I₂ ; I ; P ; Q ; S .

34.3. Дано: R₁ = 3Ом; R₂ = 6Ом; X_С1 = 4Ом; X_С2 = 8Ом; I₂ = 4А  (рис.76).

Знайти: I₁ ; I ; U ; P ; Q ; S .

34.4. Дано: R₁ = 24Ом; R₂ = 12Ом; X_С1 = 32Ом; X_С2 = 16Ом;

 U = 120В (рис.76).

Знайти:  I₁ ; I₂ ; I ; P ; Q ; S .

34.5. Дано: R₁ = 16Ом; R₂ = 6Ом; X_С1 = 12Ом; X_С2 = 8Ом;

 P₁ = 64Вт  (рис.76).

Знайти: I₁ ; I₂ ; I ; U ; Q ; S .

34.6. Дано: R₁ = 64Ом; R₂ = 24Ом; X_С1 = 48Ом; X_С2 = 32Ом;

 P₂ = 384Вт  (рис.76).

Знайти: I₁ ; I₂ ; I ; U ; Q ; S .

34.7. Дано: R₁ = 12Ом; R₂ = 8Ом; X_С1 = 16Ом; X_С2 = 6Ом;

 S₁ = 180В·A (рис.76).

Знайти:  I₁ ; I₂ ; I ; U; P; Q.

34.8. Дано: R₁ = 4Ом; R₂ = 8Ом; X_С1 = 3Ом; X_С2 = 6Ом; S₂ = 40В·A (рис.76).

Знайти:  I₁ ; I₂ ; I ; U; P; Q.

34.9. Дано: R₁ = 3Ом; R₂ = 6Ом; X_С1 = 4Ом; X_С2 = 8Ом;

 Q_С1 = – 256вар (рис.76).

Знайти:  I₁ ; I₂ ; I ; U; P ; S .

34.10. Дано: R₁ = 8Ом; R₂ = 12Ом; X_С1 = 6Ом; X_С2 = 16Ом;

 Q_С2 = – 144вар (рис.76).

Знайти:  I₁ ; I₂ ; I ; U; P ; S .

34.11. Дано: R₁ = 4Ом; R₂ = 6Ом; X_С1 = 3Ом; X_С2 = 8Ом; U_R1 = 40В (рис.76).

Знайти:  I₁ ; I₂ ; I ; P ; Q ; S .

Задача 35. Коло змінного струму містить різні елементи (резистори, індуктивність, ємності), які з’єднані в дві паралельні вітки. Схема кола наведена на рис.77. Для заданого кола  визначити  величини, які не задані в умові задачі.

 

Рис. 77.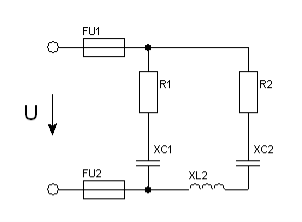

35.1. Дано: R₁ = 4Ом; R₂ = 8Ом; X_L2 = 12Ом;  X_С1 = 3Ом; X_С2 = 6Ом;

 P₂ = 288Вт  (рис.77).

Знайти: I₁ ; I₂ ; I ; U ; Q ; S .

35.2. Дано: R₁ = 8Ом; R₂ = 4Ом; X_L2 = 5Ом;  X_С1 = 6Ом; X_С2 = 8Ом;

 U = 20В (рис.77).

Знайти:  I₁ ; I₂ ; I ; P ; Q ; S .

35.3. Дано: R₁ = 64Ом; R₂ = 24Ом; X_L2 = 40Ом;  X_С1 = 48Ом; X_С2 = 8Ом;

 P₁ = 64Вт  (рис.77).

Знайти: I₁ ; I₂ ; I ; U ; Q ; S .

35.4. Дано: R₁ = 6Ом; R₂ = 8Ом; X_L2 = 4Ом;  X_С1 = 8Ом; X_С2 = 10Ом;

 I₁ = 5А  (рис.77).

Знайти: I₂ ; I ; U ; P ; Q ; S .

35.5. Дано: R₁ = 3Ом; R₂ = 6Ом; X_L2 = 10Ом;  X_С1 = 4Ом; X_С2 = 2Ом;

 I₂ = 3А  (рис.77).

Знайти: I₁ ; I ; U ; P ; Q ; S .

35.6. Дано: R₁ = 4Ом; R₂ = 6Ом; X_L2 = 2Ом;  X_С1 = 3Ом; X_С2 = 10Ом;

 Q_С2 = – 432вар (рис.77).

Знайти:  I₁ ; I₂ ; I ; U; P ; S .

35.7. Дано: R₁ = 12Ом; R₂ = 32Ом; X_L2 = 30Ом;  X_С1 = 16Ом; X_С2 = 6Ом;

 Q _L2 = 120вар (рис.77).

Знайти:  I₁ ; I₂ ; I ; U; P ; S .

 35.8. Дано: R₁ = 32Ом; R₂ = 16Ом; X_L2 = 6Ом;  X_С1 = 24Ом; X_С2 = 18Ом;

U_С2 = 108В (рис.77).

Знайти:  I₁ ; I₂ ; I ; P ; Q ; S .

35.9. Дано: R₁ = 4Ом; R₂ = 8Ом; X_L2 = 12Ом;  X_С1 = 3Ом; X_С2 = 6Ом;

U_R1 = 8В (рис.77).

Знайти:  I₁ ; I₂ ; I ; P ; Q ; S .

35.10. Дано: R₁ = 24Ом; R₂ = 16Ом; X_L2 = 8Ом;  X_С1 = 32Ом; X_С2 = 20Ом;

Q_С2 = – 1280вар (рис.77).

Знайти:  I₁ ; I₂ ; I ; U; P ; S .

 

Л І Т Е Р А Т У Р А.

1. Гуржій А.М.,  Сільвестров А.М., Поворознюк Н.І. Електротехніка з основами промислової електроніки. – К.: Форум, 2002. – 382 с.: іл.

2. Китаев В. Е., Шляпинтох Л. С. Электротехника с основами промышленной электроники. М., «Высшая школа», 1973.  

3. Попов Ю. П.,  Шовкошитний І.І .Основи електротехніки, радіо- та мікроелектроніки. – Львів: Оріяна-Нова, 2001. – 167 с.

4. Принц М.В., Цимбалістий В.М. Трансформатори. Монтаж, обслуговування та ремонт. – Львів: Оріяна-Нова, 2007. – 184 с.