Урок на тему: "Подільність натуральних чисел"

5 клас

Математика

Тема. Підсумковий урок теми “ Подільність натуральних чисел”

Мета уроку:  узагальнити та систематизувати знання учнів про подільність натуральних чисел; повторити  ознаки подільності; удосконалити  вміння розкладати числа на прості множники, знаходити НСД і НСК; розвивати   логічне мислення, створювати ситуації зацікавленості та позитивні емоції по відношенню до навчальної діяльності, виховувати здатність до співпраці, математичну та інформаційну компетентності, сприяти формуванню і розвитку інтелектуальних та творчих  здібностей учнів.

Тип уроку: узагальнення та систематизація знань.

Форма проведення уроку: урок – подорож, урок- гра.

Обладнання: малюнок потяга, інтерактивна дошка, додаток learnangapps.org, картки, таблиця для запису результатів гри, казка.

ХІД УРОКУ

І. Організаційний етап.

Добрий день!

Сіли рівно, озирніться.

Один одному всміхніться

Й за роботу дружно всі беріться.

 

Учитель:

 Сьогодні ми повторимо та узагальнимо наші знання з теми “Подільність натуральних чисел”, які будемо застосовувати при розв’язуванні задач і вправ. Це- урок- подорож по країні “ Подільність натуральних чисел”. Подорожувати будемо Зимовим потягом ( вивішує малюнок потяга ).

 

 

Відправляємося подорожувати у трьох вагонах

( клас розбивається на три команди, діти придумують назву  команди ).

 

ІІ. Актуалізація опорних знань. Інтерактивні  вправи. Додаток learningapps.org.

Перша станція «СІЧНЕВА СТАРТОВА»

 Щоб сісти  у вагон потрібно придбати квиток, для придбання квитка – отримайте бали за виконання завдань. (Чим дорожчий квиток, тим комфортніше місце в потязі!)

 

1. Заповніть пропуски. Адреса посилання https://learningapps.org/watch?v=po8dxs93k19

 

Число, на яке ділиться дане число , називається …

Число, яке ділиться на дане число, називається …

Число, яке має лише два дільники , називається…

Число, яке має більше двох дільників, називається…

Найменшим простим числом є число…

Число … не є ні складеним ні простим.

 

2 . Користуючись ознаками подільності , розподіліть числа у відповідні клітинки. Адреса посилання https://learningapps.org/watch?v=pdcu0uxzj19

 

 

 

 

 

 

 

 

 

 

 

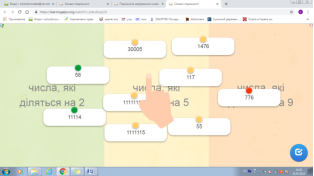
Повторюються ознаки подільності натуральних чисел.

 

ІІІ. Узагальнення і систематизація знань. Удосконалення вмінь.

Учитель: Наша подорож продовжується.

А ось і перша зупинка . Це станція «ЗИМОВА ДЕТЕКТИВНА». 

Інтерактивна гра «Незакінчене речення»

Знайшли аркуш паперу на якому розмиті цифри. Потрібно замінити *  потрібною цифрою. Кожному вагону дається  записана на окремих аркушах таблиця. Учні повинні по черзі заповнити їх. Числа повинні ділитися на:

І вагон на 9;                         ІІ вагон на 2;                                ІІІ вагон на 3.   

23*4                                         145*                                               38*2

12*4                                         421*                                               1*46

56*2                                         36*0                                               32*4    

94*5                                         116*                                               19*5

( учні виконують завдання і після його перевірки оголошується провідник у кожному вагоні ).

 Учитель: вирушаємо далі. Аж ось ми наближаємося до казкового лісу.

Так, це станція «КАЗКОВА – ТЕОРЕТИЧНА».

Послухаємо казку.

Відбувалося це у казковому осінньому лісі, на широкій галявині.

Число 28 вирішило запросити до себе в гості своїх дільників, менших від нього самого. Першою прибігла одиниця, за нею двійка, за нею 4 ; 7; 14. Напишіть список усіх гостей Числа 28.( 1; 2; 4; 7;14 ).

Коли всі гості зібралися, Число 28 побачило, що їх небагато. Воно засумувало і запропонувало, щоб кожний із гостей запросив ще і своїх дільників. Скільки прийде нових гостей? ( нових гостей не буде ).

Одиниця пояснила Числу 28, що за такої умови нові гості до нього не прийдуть: адже якщо яке-небудь число b є дільником для числа а, а число с- дільник числа b, то с буде дільником і числа а.

Перевірте це для числа 30. Знайдіть усі дільники і для кожного з них його дільники. Хто перший виконає завдання- приносить своєму вагону 2 бали.

Щоб заспокоїти Число 28, його гості з’єдналися знаком “+”. І, о диво! Сума дорівнювала самому числу 28 !. Одиниця сказала, що будь-яке число, яке дорівнює сумі своїх менших дільників, називається досконалим. Отже, число 28 – досконале число. Зраділо Число 28 і запитало, які є ще досконалі числа? Всезнаюча Одиниця пояснила, що досконалі числа зустрічаються дуже рідко: серед чисел до мільйона тільки чотири досконалих. Число 28 єдине двоцифрове  досконале число; є тільки одне трицифрове досконале число це 496 .

Число 29 вирішило також запросити до себе в гості своїх менших дільників. Першою, як завжди, прибігла Одиниця. Хто ще прийшов у гості? Що можна сказати про Число 29? Яке воно? Числам сподобалося запрошувати до себе у гості своїх дільників.  Тільки одне число не дочекалося гостей. Що це за число? Скільки раз воно само побувало у гостях? У яких чисел був тільки один гість? Що це за гість? Ось і казочці кінець, а хто слухав і працював - молодець.

А зараз швидка лічба: хто швидше порахує. За кожен, вірно порахований приклад, вагон одержує 2 бали.

(( 9+91): 5+30):5=            ( 100:25 +32):9-4=            ( 205+11):4-54+2=

Станція «ЧАРІВНА КВІТКА»

Знайдіть НСК і НСД чисел, розташованих на листочках квіточок, та зафарбуйте відповідні пелюстки квіток.

 

 

 

 

 

 

 

 

 

 

 

 

                                     

 

 

 

 

 

 

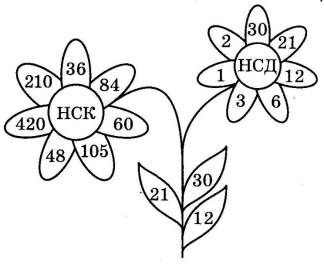
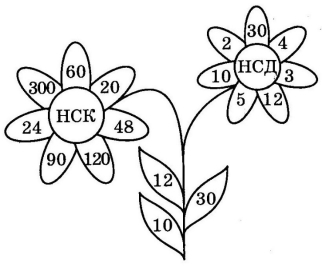
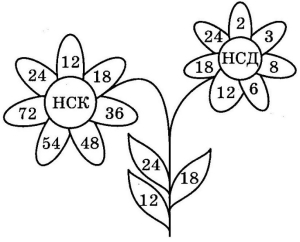
Станція «ОСІННІЙ БУКЕТ»

 

Яку найбільшу кількість

букетів можна зібрати

з 336 троянд,  528 гербер,

720 лілій?

 

 

 

 

 

 

 

 

ІV. Підсумок уроку. Рефлексія.

Учитель: продовжуємо нашу подорож. ( звучить музика). Ось ми наближаємося до наступної зупинки – це станція “ МАТЕМАТИЧНА ЗАГАДКОВА”.

По черзі кожному вагону загадується загадка. За кожну правильну відповідь   діти одержують один бал.

 

1.          На число це - знайте діти, -

Заборонено ділити, проте множити чудово-

Зразу ж відповідь готова.

Не роби собі проблем,

Обережним будь з ….( нулем).

 

2.          Ці числа є великі,

а є і малюки,

проте з них кожне має

лише два дільники.

Як відомо, числа ті

Називаються….( прості).

 

3.          Ці числа не прості, а інші,

В них дільників не два, а більше.

Для них теж назву знайдемо,

Ці числа звуться….( складені).

4.          Є лише одне таке

Число парне і просте.

Це- запам’ятай слово-

Всім відоме число...( два).

 

5.          Як довідатись мені,

 чи число просте чи ні?

Як квадрат числа узнати,

Так, щоб час не витрачати?

Знають учні й учениці:

Допоможуть тут …( таблиці). 

 

6.          Щоб узнати швидко й стисло,

чи ділитись будуть числа,

правила такі в нас-

відповідь знайдемо враз.

Заслуговують подяки,

Це- подільності…( ознаки).

 

Ось і закінчилася наша подорож по країні “ подільності чисел”.

Учитель підводить підсумки гри, оцінює учнів. Визначаються переможці гри.

Потім підводить підсумок вивчення теми.

 

V. Домашнє завдання

Тестова самостійна робота

№ 1°. Дільниками числа 14 є числа:
А	Б	В	Г
14;  28;  42;  56	2;  7;  14;  28	1;  2;  7;  14	1;  2;  3;  7;  14
№ 2°. Числами, кратними числу 6 є:
А	Б	В	Г
6;  12;  18	1;  2;  3	12;  19;  24	6;  16;  36
№ 3°. Знайдіть усі прості розв’язки нерівності 35 ≤  х ≤ 53:
А	Б	В	Г
37; 41; 43; 47	37; 41; 47; 53	35; 37; 41; 43; 47	37; 41; 43; 47; 53
№ 4°. Число 16 є взаємно простим із числом:
А	Б	В	Г
32	21	48	54

№ 5°. Установіть відповідність між умовою (1–4) та числом, що задовольняє цю умову  (А–Д): 

1	На 5 ділиться число…		А	7 315
2	На 9 ділиться число…		Б	7 419
3	Ділиться на 3 і не ділиться на 2 число…		В	56
4	На 14 ділиться число…		Г	54 774
			Д	773

№ 6˙. Між якими простими числами буде розташований найбільший спільний дільник чисел 720 і 280.