Стандартні графічні процедури і функції для роботи з дугами, колами, еліпсами.

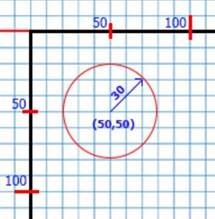
Circle(X,Y:integer; радіус : word) - процедура малює окружність поточним кольором. Точка (X,Y) - центр окружності, а "радіус" - її радіус.

Приклад: Circle(50,50,30)

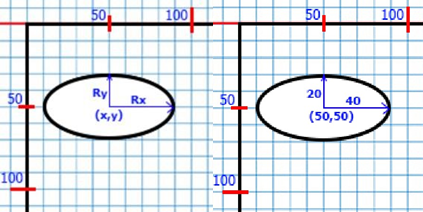FillEllipse(X,Y:integer;Xpaдіyс,Ypaдіус:word) - процедура вичерчує зафарбований еліпс, використовуючи точку з координатами (Х,Y), як центр, а "Храдіус" і "Yрадіус" - у якості радіусів на горизонтальній та вертикальній осях. Контур еліпса креслиться кольором і типом лінії, що встановлені процедурами SetLineStyle і SetColor, тип і колір зафарбування встановлюється за допомогою процедури SetFillStyle.  

Дану процедуру можна використовувати для побудови кругів, задавши однакові радіуси.  

Приклад: FillEllipce(50,50,40,20)

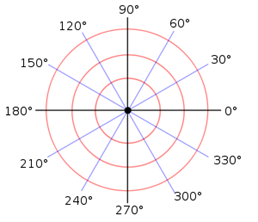
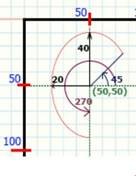
Перед тим,   як      почати        працювати з наступними процедурами, потрібно пригадати поняття і значення кутів. Даний рисунок слід запам'ятати, або завжди тримати перед собою, при здійсненні побудов. Відлік градусної міри кута починається з 0, та зростає проти руху годинникової стрілки, і закінчується значенням 360°, яке називається повним кутом (2π). Значення 180° - розгорнутий кут (π).

Arc(X,Y:integer; поч_кут, кін_кут, радіус:word) - програмна процедура, результатом роботи якої є дуга окружності з центром в точці (X,Y) і радіусом "радіус". Дуга креслиться від початкового кута ("поч_кут") до кінцевого кута ("кін_кут") проти годинникової стрілки. При цьому використовується поточний колір малювання.

            Приклад:      

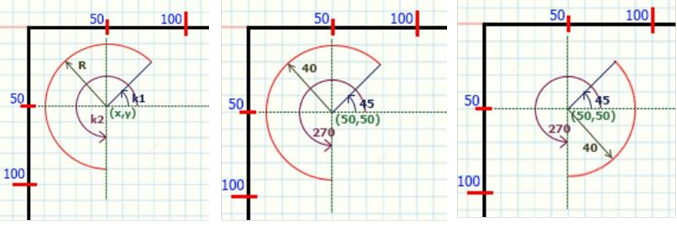
                Arc(x,y,k1,k2,R)                 Arc(50,50,45,270,40)              Arc(50,50,270,45,40)

Ellipse(X,Y:integer; поч_кут, кін_кут:word; paдХ,paдY:word) - процедура малює еліптичну дугу, використовуючи (X,Y), як точку центра і "радХ", "paдY" - як радіуси на горизонтальній і вертикальній осях. Дуга еліпса малюється від початкового кута (параметр "поч_кут") до кінцевого кута (параметр "кін_кут") проти годинникової стрілки поточним кольором. Приклад:  

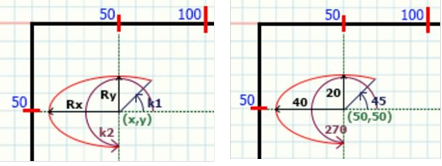
       Ellipse (x,y,k1,k2,Rx,Ry)        Ellipse (50,50,45,270,40,20) Ellipse (50,50,270,45,20,40)

PieSlice (Х, Y: integer; поч_кут, кін_кут R : word); - процедура вичерчує і заповнює поточним кольором сектор кола радіусом R. Точка (X,Y) - центр окружності, а сектор малюється від початкового до кінцевого кута (від меншого до більшого). Тип і колір зафарбування попередньо задається процедурою SetFillStyle. Приклад:

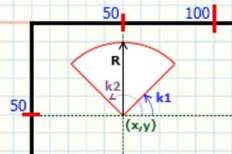
PieSlice (x,y,k1,k2,R)     PieSlice (50,50,45,135,40)        PieSlice (50,50,135,45,40) Sector (X, У : integer; поч__кут, кін_кут, Х_Радіус, Y_Радіус : word); - процедура вичерчує і заповнює еліптичний сектор. (Х,Y) - центр окружності, "Х_Радіус", "Y_Радіус" - горизонтальний і вертикальний радіуси. Сектор креслиться від початкового кута "поч_кут" до кінцевого кута "кін_кут" (від меншого до більшого). Сектор малюється поточним кольором і зафарбовується з використанням зразка зафарбування і кольорів, заданих за допомогою процедури SetFillStyle.

            Приклад:      

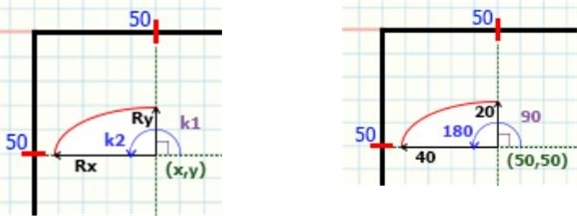
        PieSlice (x,y,k1,k2,Rx,Ry)       PieSlice (50,50,90,180,40)     PieSlice (50,50,180,90,40)

При побудові даних фігур слід звернути увагу на те, що процедури Arc та Ellipse завжди здійснюють побудови проти годинникової стрілки, від початкового до кінцевого кута, в тому порядку як вони задані в процедурах, на відміну від процедур PieSlice та Sector, котрі завжди здійснюють побудову від меншого кута до більшого, не залежно від того, як вони записані в процедурі.

Формування практичних вмінь і навичок.

1.     Скласти програму, яка будує усміхнене обличчя.

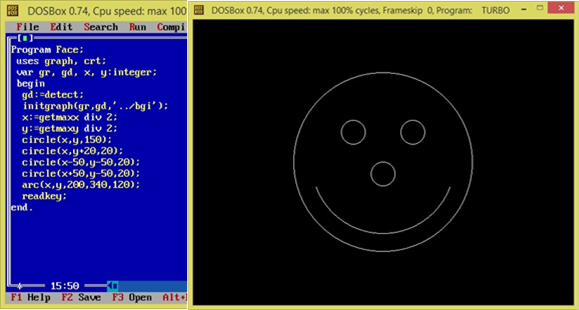
Program Face;  uses graph, crt;  var gr, gd, x, y:integer;  begin   gd:=detect; initgraph(gr,gd,'');   x:=getmaxx div 2;   y:=getmaxy div 2; circle(x,y,150);   circle(x,y+20,20);   circle(x-50,y-50,20); circle(x+50,y-50,20);   arc(x,y,200,340,120);   readkey; end.

2.     Скласти програму, яка будує чебурашку.

Program Cheburashka;  uses graph, crt;  var gr, gd, x, y:integer;  begin gd:=detect;   initgraph(gr,gd,'');   x:=getmaxx div 2;   y:=getmaxy div 2; ellipse(x,y+90,360,0,70,80);   fillellipse(x,y+50,30,40); circle(x,y-50,60);   circle(x,y-50,45);   fillellipse(x,y-45,8,5); arc(x,y-50,240,300,30);   circle(x-20,y-65,8);   fillellipse(x-20,y-65,3,3); circle(x+20,y-65,8);   fillellipse(x+20,y-65,3,3); fillellipse(x-110,y-80,30,30);   circle(x-110,y-80,55); fillellipse(x+110,y-80,30,30);   circle(x+110,y-80,55); ellipse(x-50,y+177,360,0,30,20);   ellipse(x+50,y+177,360,0,30,20); ellipse(x-75,y+90,50,315,15,40);   ellipse(x+75,y+90,225,130,15,40);   readkey; end.

За допомогою графічного режиму Pascal можна знаходити графічні розв’язки різноманітних математичних задач. Наприклад, знайти координати точок перетину двох кіл

Розв’язок цієї задачі, при всій своїй незвичності, зводиться до розв’язку квадратного рівняння.

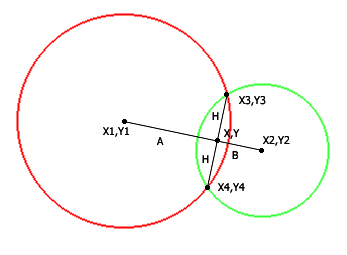Дано два кола, перше з центром в точці 1 з координатами X1, Y1 і радіусом R1. Друге з центром в точці 2 з

координатами X2, Y2 і радіусом R2

У точках перетину знаходяться шукані точки 3 і 4 з координатами, відповідно X3, Y3 та X4, Y4.

Центральна точка 0 - точка перетину всіх ліній, з координатами X, Y.

Розглянемо два прямокутних трикутника 103 і 203 зі спільним катетом 03. Гіпотенузи нам відомі - це радіуси R1, точки 13 і R2, точки 23.

Знаючи координати X1, Y1 і X2, Y2 легко можна знайти відстань D між ними.

Відрізок H однаковий, значить легко можна скласти систему рівнянь.

•      X1, Y1, R1 - Параметри першого кола

•      X2, Y2, R2 - Параметри другого кола

•      X, Y - Координати центру перетинів всіх ліній

•      A - Відстань від центру першого кола до точки перетину всіх ліній

•      B - Відстань від центру другого кола до точки перетину всіх ліній

•      H - Відстань від точки перетину всіх ліній до точок перетину кіл

•      D - Відстань між центрами кіл

•      X3, Y3 - Координати першої точки перетину

•      X4, Y4 - Координати другої точки перетину

•      R - Кількість точок перетину 

Результат

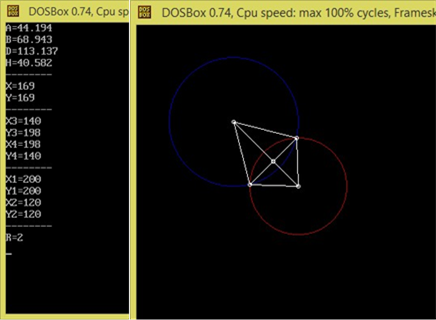
Код програми

uses Graph; var   grDriver : Integer;

  grMode   : Integer;

   X1,X2,Y1,Y2,R1,R2:Integer;

   A,B,H,D:Real;

   X,Y:Integer;

   X3,X4,Y3,Y4:Integer;

   R:Integer;

Begin

     X1:=200;

     Y1:=200;

     R1:=60;

     X2:=120;

     Y2:=120;

     R2:=80;

     R:=2;

     D:=sqrt(sqr(X2-X1)+sqr(Y2-Y1));

     If (D<=(R1+R2)) AND (D>=ABS(R1-R2)) Then

     Begin

          B:=(sqr(R2)-sqr(R1)+sqr(D))/(2*D);

          A:=D-B;

          H:=sqrt(sqr(R2)-sqr(B));

          X:=round(X1+(X2-X1)/(D/A));

          Y:=round(Y1+(Y2-Y1)/(D/A));

          X3:=round(X-(Y-Y2)*H/B);

          Y3:=round(Y+(X-X2)*H/B);

          X4:=round(X+(Y-Y2)*H/B);

          Y4:=round(Y-(X-X2)*H/B);

          WriteLn('A=',A:3:3);

          WriteLn('B=',B:3:3);

          WriteLn('D=',D:3:3);

          WriteLn('H=',H:3:3);

          WriteLn('--------');

          WriteLn('X=',X);

          WriteLn('Y=',Y);

          WriteLn('--------');

          WriteLn('X3=',X3);

          WriteLn('Y3=',Y3);

          WriteLn('X4=',X4);

          WriteLn('Y4=',Y4);

     End Else R:=0;

     If D=R1+R2 Then R:=1;

     WriteLn('--------');

     WriteLn('X1=',X1);

     WriteLn('Y1=',Y1);

     WriteLn('X2=',X2);

     WriteLn('Y2=',Y2);

     WriteLn('--------');

     WriteLn('R=',R);

     ReadLn;

    grDriver := Detect;

    InitGraph(grDriver,grMode,'../bgi');

       SetColor(Red);

       Circle(X1,Y1,R1);

       SetColor(Blue);

       Circle(X2,Y2,R2);

       SetColor(White);

       Circle(X1,Y1,2);

       Circle(X2,Y2,2);

       Line(X1,Y1,X2,Y2);

       If (D<=(R1+R2)) AND (D>=ABS(R1-R2)) Then

       Begin

            Circle(X3,Y3,2);

            Circle(X4,Y4,2);

            Circle(X,Y,2);

            Line(X3,Y3,X4,Y4);

            Line(X4,Y4,X1,Y1);

            Line(X4,Y4,X2,Y2);

            Line(X3,Y3,X1,Y1);

            Line(X3,Y3,X2,Y2);

       End;

       ReadLn;

    CloseGraph;

End.