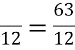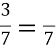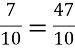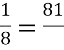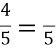Урок з математики 5 клас "Мішані числа"
Конспект, презентація та роздатковий матеріал до узагальнюючого уроку з математики у 5 класі до теми "Мішані числа". Метою уроку є узагальнити та систематизувати раніше набуті вмінняі та навички.
- ДО УРОКУ.pptx pptx
- УРОКУ.docx docx
- матеріал.docx docx
- ~$ПРЕЗЕНТАЦІЯ ДО УРОКУ.pptx pptx
- Показати всі файли
План-конспект уроку математики в 5 класі
Тема:Мішані числа. Розв’язування вправ.
Мета:
- навчальна: продовжувати формувати навички учнів розв’язувати вправи, що передбачають використання звичайних дробів, додавання та віднімання звичайних дробів, повторити правила знаходження невідомих компонентів дій, правила порівняння дробів практичні навички розв’язування задач і вправ на додавання і віднімання дробів з однаковими знаменниками, застосовувати набуті знання в нестандартних ситуаціях;
- розвиваюча: розвивати всі види пам’яті, увагу, уяву, логічне, критичне мислення, творчі здібності, культуру записів, математичну мову, розширювати кругозір учнів;
- виховна: виховувати старанність, працьовитість, любов до праці, дружність, виховувати інтерес до предмету та науки, історії математики, використовуючи інформаційні та здоров’язберігаючі технології, повагу до однолітків, вчителів, культуру праці.
Тип уроку: урок формування вмінь та навичок
Обладнання до уроку:
- презентація до уроку;
- обладнання для мультимедійної презентації;
- картки з завданнями до перевірки домашнього завдання(2 картки);
- картки для проведення гри «Математичне лото»(за кількістю учнів);
- сигнальні картки для гри «Вірю – не вірю» (за кількістю учнів);
- плакат – карта подорожі.
Хід уроку.
- Організаційний момент.
Організація класу до уроку, налаштування до роботи.
- Оголошення цілей уроку та мотивація навчальної діяльності учнів.
Діти, сьогодні у нас черговий урок з теми « Звичайні дроби». Ви вже знаєте, що таке звичайний дріб, вмієте порівнювати дроби, додавати та віднімати дроби з однаковими знаменниками. А тепер спробуємо, що ми повинні зробити на уроці, чому ми повинні або можемо навчитися. Отже …( Вислухати пропозиції учнів, скоригувати відповіді,зробити висновки та сформулювати цілі та завдання уроку)
Девіз уроку:
Без знання дробів ніхто не може визнавати, що знає математику Цицерон
- Перевірка домашнього завдання.
1.Робота з картками. 2 учні виконують на місці завдання на карточках. Завдання в тестовій формі, подібні до завдань з домашньої роботи).
2. Фронтальна перевірка домашнього завдання.
3. Вчитель збирає картки і робить короткий підсумок по виконанню домашнього завдання.
- Формування знань, вмінь та навичок, здобутих на попередніх уроках
Сьогодні на уроці ми здійснимо подорож на кораблі «МІФ» (математика і фантазія) по Океану Знань і відвідаємо дуже цікаві місця
Пункт 1.Місто Історичне
Першим ми відвідаємо місто Історичне. Там нашими однокласниками зібраний дуже цікавий історичний матеріал про дробові числа. Отже, послухаємо (інформацію готують учні, а вчитель допомагає при оформленні слайду).
З давніх часів людям доводилося не тільки рахувати предмети (для цього були потрібні натуральні числа), але й вимірювати довжину, площу, вести розрахунки за куплені і продані товари. Не завжди результат вимірювання або вартість товару можна було виразити натуральними числами. Тож з’явилися дроби.
Римський оратор і письменник Цицерон казав, що без знання дробів ніхто не може визнавати, що знає математику.
А у німців збереглося таке прислів’я: «Потрапити в дроби», що означає потрапити в важке становище.
Слово «дріб» з'явилося в VIIIст., воно походить від дієслова «дробити» - розбивати на частини, ламати. В перших підручниках з математики дроби так і називалися - «ламані» числа.
Спочатку для запису дробів не використовувалася риска дробу. Вона почала застосовуватися близько 300 років тому назад. Першим європейським ученим, який почав використовувати і поширювати сучасний запис дробу, був італійський купець і мандрівник, син міського писаря Фібоначчі Леонардо Пізанський в 1202 році. Він ввів слово «дріб».
Дроби в Стародавньому Єгипті
Перший дробом, з яким познайомилися люди, була, напевно , половина. За нею послідували ![]() , потім
, потім ![]() і т.д., тобто одиничні або основні дроби. У них чисельником є завжди одиниця . Єгиптяни писали на папірусі , тобто на свитках , виготовлених з стебла великих тропічних рослин - папірусів. У папірусі Ахмеса є таблиці для представлення деяких дробів у вигляді суми одиничних дробів .
і т.д., тобто одиничні або основні дроби. У них чисельником є завжди одиниця . Єгиптяни писали на папірусі , тобто на свитках , виготовлених з стебла великих тропічних рослин - папірусів. У папірусі Ахмеса є таблиці для представлення деяких дробів у вигляді суми одиничних дробів .
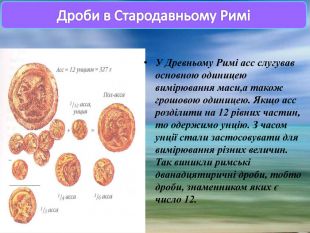
Дроби в Стародавньому Римі.
У Древньому Римі асс слугував основною одиницею вимірювання маси,а також грошовою одиницею. Якщо асс розділити на 12 рівних частин, то одержимо унцію. З часом унції стали застосовувати для вимірювання різних величин. Так виникли римські дванадцятиричні дроби, тобто дроби, знаменником яких є число 12. Замість ![]() римляни говорили «одна унція»,
римляни говорили «одна унція», ![]() – «п’ять унцій» і т.д. Три унції називали чвертю, чотири унції-третиною, шість унцій-половиною.
– «п’ять унцій» і т.д. Три унції називали чвертю, чотири унції-третиною, шість унцій-половиною.
Дроби в Стародавній Греції.
В Греції поряд з одиничними, «єгипетськими», дробами застосовувались і звичайні дроби. Посеред різних записів зустрічався і такий: зверху – знаменник, під ним – чисельник. Наприклад, ![]() означало три п’ятих. Ще за 2-3 століття до Евкліда і Архімеда греки вільно володіли арифметичними діями з дробами.
означало три п’ятих. Ще за 2-3 століття до Евкліда і Архімеда греки вільно володіли арифметичними діями з дробами.
Дроби в Київській Русі.
У Київській Русі дроби називали частинами, пізніше – ламаними числами. Найпоширенішими з них були:
![]() - полтинник,
- полтинник, ![]() - четь,
- четь, ![]() - півчеть,
- півчеть, ![]() - треть,
- треть, ![]() - півтреть,
- півтреть, ![]() - півпівтреть.
- півпівтреть.
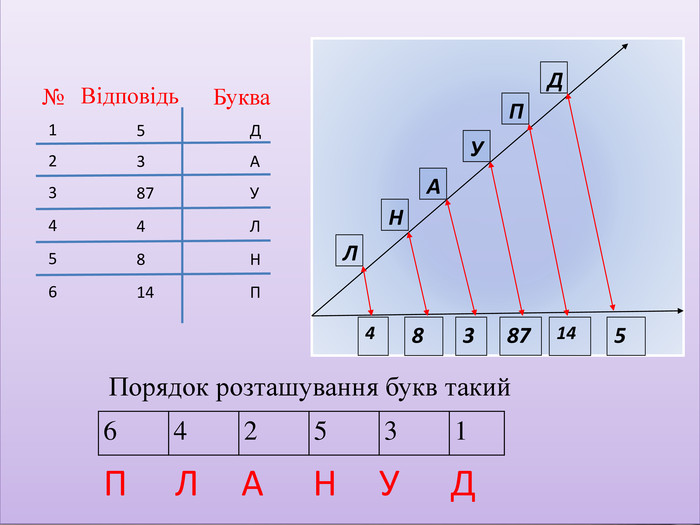
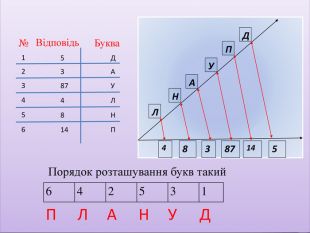
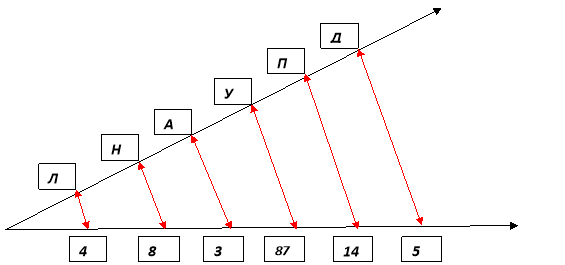
Дізнатися, хто першим ввів назви «чисельник» і «знаменник», вам допоможе таке завдання (Спочатку виконуються дії, заповнюються пропуски , потім у клітинках праворуч пишуть відповіді та відповідні до них букви. Далі ці букви розташовують у запропонованому порядку та отримують слово)
|
1 |
4 |
|
2 |
5 |
|
3 |
12 |
|
4 |
… |
|
5 |
10 |
|
6 |
2 |
|
1 |
5 |
Д |
|
2 |
3 |
А |
|
3 |
87 |
У |
|
4 |
4 |
Л |
|
5 |
8 |
Н |
|
6 |
14 |
П |
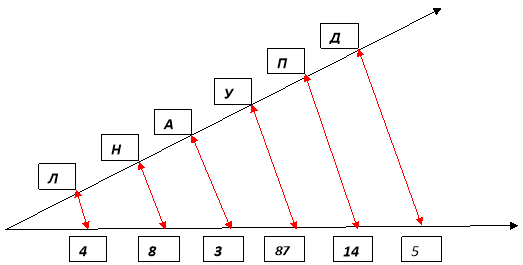 Порядок розташування букв такий
Порядок розташування букв такий
|
6 |
4 |
2 |
5 |
3 |
1 |
Назви «чисельник» і «знаменник» ввів в XIII ст. Максим Плануд – грецький монах, учений – математик.
Пункт 2. Порт Теоретичний.
На « якорях» на карті запропоновані питання,відповіді на які будуть перепустками до наступого пункту подорожі. Учні по черзі виходять до карти, обирають «якір» з відповідним питанням і дають відповідь.
- Що показує чисельник та знаменник дробу?
- Який дріб дорівнює одиниці?
- Який дріб називається правильним?
- Як виділити цілу та дробову частину з неправильного дробу?
- Як порівняти дроби з однаковими знаменниками?
- Який дріб називається неправильним?
- Як додати два дроби з однаковими знаменниками?
- Як неправильний дріб подати у вигляді мішаного числа ?
Пункт 3.Архіпелаг Розв’язаних Рівнянь.
Наступним пунктом нашої подорожі буде Архіпелаг Розв’язаних Рівнянь . Для його проходження потрібно виконати № 754.
Робота з підручником № 754, по 2 учні.

Пункт 4. Бухта «Веселі рибки». Фізкультхвилинка.
Рибки плавають в водиці,
Рибкам весело гулять.
Хочемо ми з рибками
разом попірнать.
Раз- прогнулись, потягнулись,
На носочки піднялись.
Вліво, вправо повернулись,
Один одному всміхнулись.
Рибки хвостиком махнули,
Рибки воду сколихнули
І на дно морське пірнули.
Добре всі ми відпочили
І за парти тихо сіли.
Пункт 5. Острів Порівняння
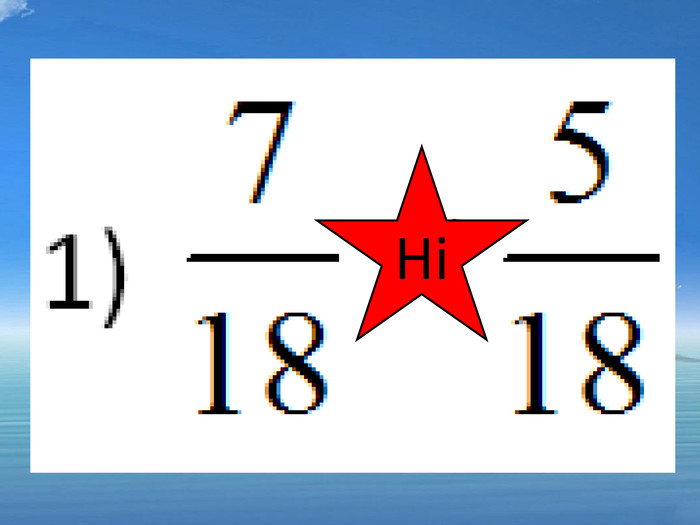
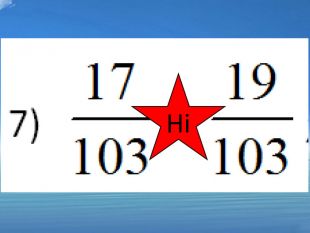
Гра «Вірю-не вірю» з сигнальними картками. На слайдах з’являються приклади, учні, за допомогою сигнальних карток, сигналізують правильно чи не правильно розв’язані приклади (зелений колір – «так», червоний – «ні»)
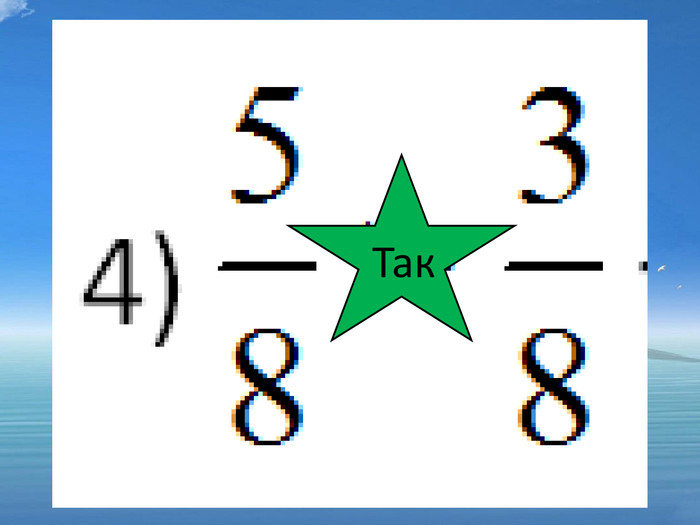
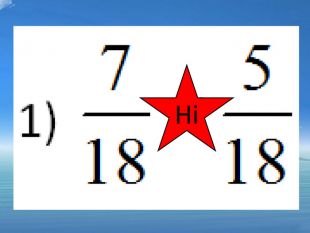
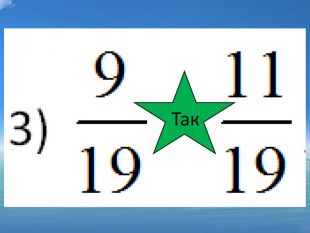
1) ![]() ; ні 2)
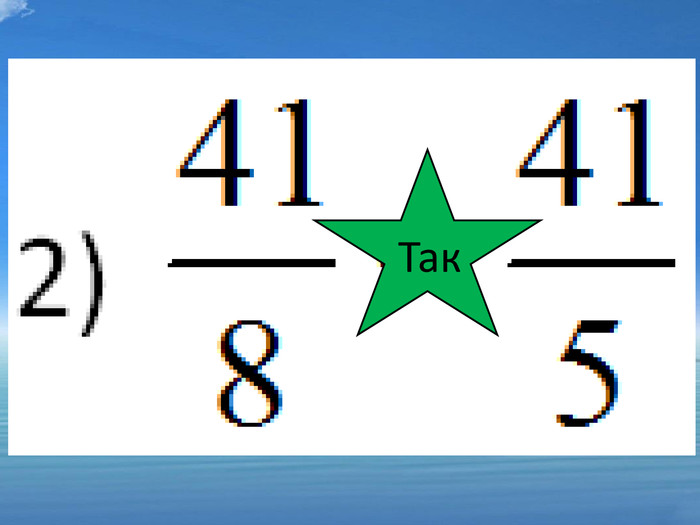
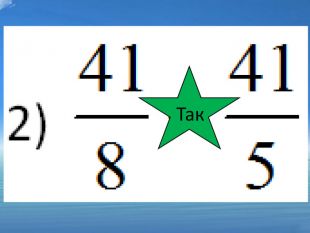
; ні 2) ![]() ; так 3)
; так 3) ![]() ; так 4)
; так 4)![]() так
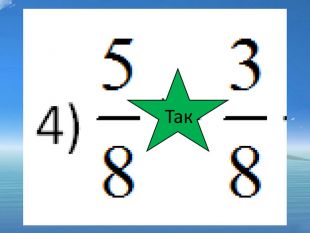
так
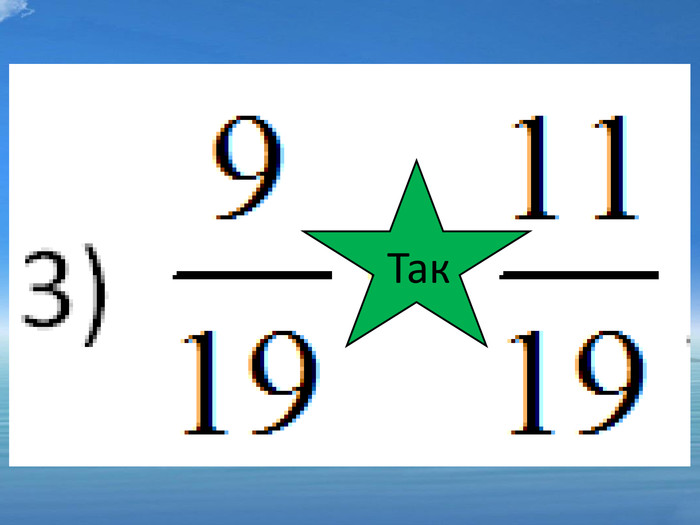
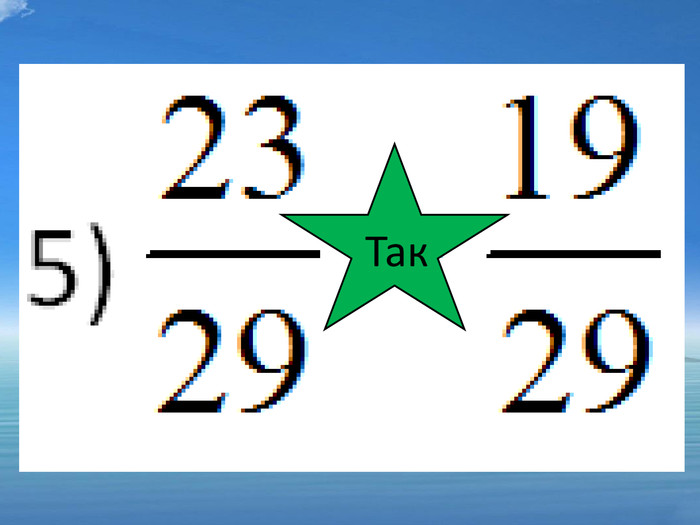
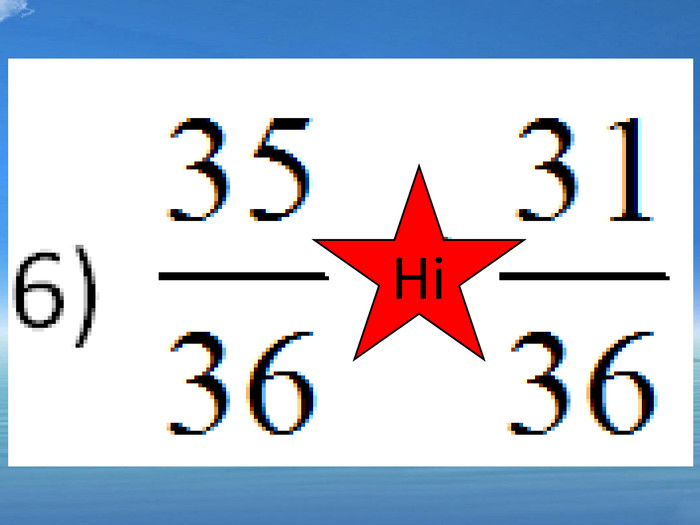
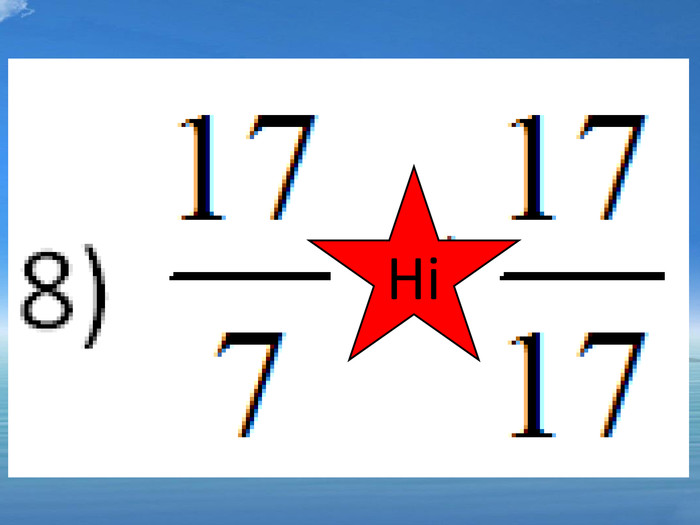
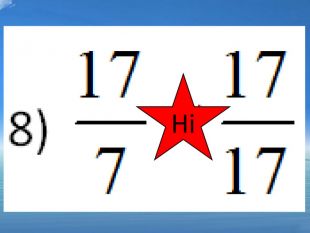
5)![]() ; так 6)
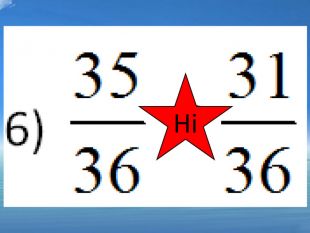
; так 6) ![]() ; ні 7)
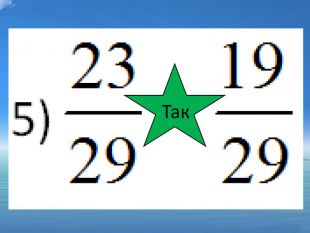
; ні 7) ![]() ; ні 8)
; ні 8) ![]() ні
ні
Пункт 6. Гавань Математична
Учням пропонується гра Математичне лото
- Клас працює за варіантами.
- Для гри слід підготувати два варіанти карток для лото загальною кількістю за числом учнів у класі.
- Питання для обох варіантів однакові. Учитель зачитує питання, учні закреслюють у своїх картках клітинку, в якій міститься правильна відповідь. На кожне запитання відводиться 30 секунд.
- Здійснюється взаємоперевірка в парах, звіряючись з екраном
- Слід зазначити, що не всі відповіді є у картках .
1 варіант
|
7 |
24 |
|
|
|
|
|
|
3 |
< |
3 |
|
|
16 |
91 |
так |
6 |
2 варіант
|
|
45 |
6 |
36 |
|
|
> |
|
3 |
|
1 |
|
ні |
13 |
|
|
11
|
( вірна відповідь: не закреслені – 1варіант: 24; ![]() ;
; ![]() ;<; 91
;<; 91
2 варіант: ![]() ; 36;
; 36; ![]() ; ні; 11)
; ні; 11)
Питання для лото
( В дужках подані вірні відповіді )
-
Чисельник дробу
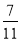 (7).
(7).
-
Знаменник дробу
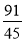 (45)
(45)
-
Найбільший правильний дріб зі знаменником 9 (
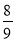 ).
).
-
Найменший неправильний дріб зі знаменником 6 (
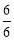 ).
).
- Розв’яжіть нерівність у натуральних числах
1<![]() <
< ![]() (16)
(16)
-
Порівняйте дроби
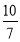 і
і 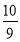 ( знайдіть у картках знак «<» або «>» ). (>)
( знайдіть у картках знак «<» або «>» ). (>)
-
Розв’яжіть рівняння:
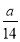 =
=  . (13)
. (13)
-
Виділіть цілу частину дробу:
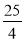 . (6
. (6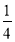 )
)
-
Яке ціле число записане дробом
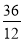 ? (3)
? (3)
-
Знайдіть число, записане дробом
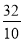 . ( 3
. ( 3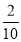 )
)
-
Чи правильна рівність
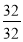 =
=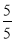 ? (так)
? (так)
-
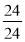 =? (1)
=? (1)
Пункт 7. Пристань Ерудитів.
Задача1. За перший тиждень плавання на кораблі команда використала ![]() т прісної води, за другий тиждень - на
т прісної води, за другий тиждень - на ![]() тон більше, ніж за перший, а за третій – на
тон більше, ніж за перший, а за третій – на![]() тон менше, ніж за перший та другий тижні разом. Скільки прісної води використала команда за всю подорож? За який тиждень було спожито найбільше води?
тон менше, ніж за перший та другий тижні разом. Скільки прісної води використала команда за всю подорож? За який тиждень було спожито найбільше води?
Задача2 Капітан запропонував комусь з команди пограти з ним в таку гру. Він називає дріб. Гравець з команди називає менший дріб. Потім капітан називає ще менший дріб, а гравець з команди – ще менший і т.д. Виграє той, хто називає дріб, менше якого вже дробів немає. Чи можна виграти в такій грі?
- Домашнє завдання
Повторити вивчений матеріал з теми «Звичайні дроби», виконати № ,№ .
Додаткове завдання – скласти кросворд з вивченої теми.
- Підсумок уроку.
Підбиття підсумків уроку, виставлення оцінок.
І, наостанок,хочу розповісти вам таке. Цікаве та влучне «арифметичне» порівняння зробив Л.М.Толстой. Він казав, що людина схожа на дріб: чисельником є те, що вона собою являє, а знаменником - те, що вона про себе думає. Чим більшої думки про себе людина,тим більший знаменник,отже, тим менше дріб. Бажаю вам бути такою людиною, у якої чисельник буде значно більшим знаменника.
Самоаналіз уроку математики у 5 класі,
проведеного вчителем математики
НВК №4 м.Хмельницького Романюк О.С.
1. Урок «Мішані числа. Розв’язування вправ» є продовженням вивчення теми «Звичайні дроби». Передбачає повторення матеріалу, що вивчався, та формування умінь та навичок учнів розв’язувати задачі та вправи.
2. На уроці чітко визначена триєдина мета:
- навчальна: продовжувати формувати навички учнів розв’язувати вправи, що передбачають використання звичайних дробів, додавання та віднімання звичайних дробів, повторити правила знаходження невідомих компонентів дій, правила порівняння дробів практичні навички розв’язування задач і вправ на додавання і віднімання дробів з однаковими знаменниками, застосовувати набуті знання в нестандартних ситуаціях;
- розвиваюча: розвивати всі види пам’яті, увагу, уяву, логічне, критичне мислення, творчі здібності, культуру записів, математичну мову, розширювати кругозір учнів;
- виховна: виховувати старанність, працьовитість, любов до праці, дружність, виховувати інтерес до предмету та науки, історії математики, використовуючи інформаційні та здоров’язберігаючі технології, повагу до однолітків, вчителів, культуру праці.
Для реалізації мети і завдань вибраний тип уроку: урок формування вмінь та навичок .
3. З метою активізації класу, налаштування учнів на успішну роботу вдало підібраний девіз уроку, повідомлена форма проведення уроку – урок подорож по Океану Знань на кораблі МІФ.
Здійснена фронтальна перевірка домашнього завдання,а також запропоновані декільком учням завдання на карточках в тестовій формі, подібні до завдань з домашньої роботи).
4. Для актуалізації опорних знань учнів проведене опитування, повторені основні поняття попереднього матеріалу. При опитуванні учні підходили до карти подорожі, самостійно «обирали» питання, що активізувало дітей, позитивно налаштовувало до роботи.
Мотивація навчально-пізнавальної діяльності учнів відбувалася протягом всього уроку, була спрямована на розвиток в учнів інтересу до навчання, потреби у різноманітних знаннях, розуміння необхідності вивченого у житті.
5. Застосовані такі форми й методи роботи при проведенні уроку:
- кодовані завдання на відпрацювання навичок перетворення неправильного дробу у мішане число та навпаки, при перетворенні мішаного числа у неправильний дріб;
- дидактична гра «Вірю - не вірю» з сигнальними картками для з метою перевірки та корекції вмінь та навичок учнів порівнювати дроби з однаковими чисельниками, з однаковими знаменниками, правильні та неправильні дроби між собою;
- робота з підручником, що передбачала виконання біля дошки учнями вправи з підручника (розв’язування рівнянь);
- дидактична гра «Математичне лото» з подальшою взаємоперевіркою;
- розв’язування задач біля дошки на застосування правил додавання на віднімання дробів з однаковими знаменниками, а також на порівняння дробів, а також розв’язування задачі логічного характеру;
6. На уроці практикую елементи самоосвіти та самовиховання. При підготовці до уроку група учнів класу самостійно підготували історичний матеріал до уроку. Це сприяло також здійсненню між предметних зв’язків на уроці математики, зокрема математика – історія та математика – інформатика. При проведенні підсумків уроку зачитаний вислів Л.М.Толстого, що розширює кругозір учнів, і також допомагає здійснювати між предметні зв’язки.Використаний індивідуальний та колективний підхід до навчання. Вважаю доцільним проведення навчальної самостійної роботи на уроці у формі дидактичної гри з подальшою взаємоперевіркою.
Пошукові завдання і проблемні запитання сприяли глибокому засвоєнню матеріалу, позитивному емоційному настрою учнів.
7. Робота окремих учнів оцінювалася, оцінки коментовані. Здійснене цінування роботи учнів всього класу.
8. Дотримання вчителем норм педагогічної етики, правил такту дозволяє досягти тісного контакту з класом, доброзичливості у стосунках між учителем та учнями.
9. Здоров’язберігаюча робота на уроці полягала у зміні видів навчальної діяльності, рівномірному навантаженні на всіх учнів класу, проведеній фізкультхвилинці, а також у тому, що при підготовці уроку були враховані вікові та індивідуальні особливості учнів: інтерес до вивчення даного предмету, розвиток загальнонавчальних умінь та навичок, добрі потенціальні можливості оволодіння математикою, розвиток уяви, бажання самостійно висловлюватись, достатньо висока мотивація, що стимулювалася використанням ефективних методів роботи на уроці.
10. 5-Д клас дуже неоднорідний по успішності. Є учні, що важко сприймають новий матеріал, але є такі, що мають високий рівень навчальних досягнень з математики.
Діти активні, організовані, дисципліновані на уроці.
Учні володіють навичками колективної та самостійної роботи. Все це враховувалось при плануванні уроку та визначенні технологій для використання на уроці.
11. Вважаю, що вдалося досягти мети, завдань, запланованих результатів уроку.
Дізнатися, хто першим ввів назви «чисельник» і «знаменник», вам допоможе таке завдання(Спочатку виконуються дії, заповнюються пропуски , потім у клітинках праворуч пишуть відповіді та відповідні до них букви. Далі ці букви розташовують у запропонованому порядку та отримують слово)
|
1 |
4 |
|
2 |
5 |
|
3 |
12 |
|
4 |
… |
|
5 |
10 |
|
6 |
2 |
|
1 |
5 |
Д |
|
2 |
3 |
А |
|
3 |
87 |
У |
|
4 |
4 |
Л |
|
5 |
8 |
Н |
|
6 |
14 |
П |
Порядок розташування букв такий
|
6 |
4 |
2 |
5 |
3 |
1 |
Прізвище, ім’я
1 варіант
|
7 |
24 |
|
|
|
|
|
|
3 |
< |
3 |
|
|
16 |
91 |
так |
6 |
-------------------------------------------------------------------------------------------
Прізвище, ім’я
1 варіант
|
7 |
24 |
|
|
|
|
|
|
3 |
< |
3 |
|
|
16 |
91 |
так |
6 |
-----------------------------------------------------------------------------------------
Прізвище, ім’я
1 варіант
|
7 |
24 |
|
|
|
|
|
|
3 |
< |
3 |
|
|
16 |
91 |
так |
6 |
Прізвище, ім’я
2 варіант
|
|
45 |
6 |
36 |
|
|
> |
|
3 |
|
1 |
|
ні |
13 |
|
|
11
|
----------------------------------------------------------------------------------
Прізвище, ім’я
2 варіант
|
|
45 |
6 |
36 |
|
|
> |
|
3 |
|
1 |
|
ні |
13 |
|
|
11
|
---------------------------------------------------------------------------------
Прізвище, ім’я
2 варіант
|
|
45 |
6 |
36 |
|
|
> |
|
3 |
|
1 |
|
ні |
13 |
|
|
11
|
-
Щіро дякую!
-
Дякую за розробку!


про публікацію авторської розробки
Додати розробку