Завдання на встановлення відповідності з алгебри 7 клас

Про матеріал

Проблема оцінювання знань школярів набула сьогодні особливої актуальності. Якість освіти безпосередньо пов’язують з системою оцінювання всіх складових навчально-виховного процесу – навчальних досягнень учнів, ефективністю роботи кожного вчителя і школи в цілому. Чим об’єктивнішим буде це оцінювання, тим якіснішою стане освіта. Визнаним у світі інструментами педагогічного оцінювання та вимірювання є тестові технології, які все частіше використовуються в школі. Потужним стимулом і викликом стало обов’язкове зовнішнє незалежне оцінювання (ЗНО) випускників шкіл. Завдання на встановлення відповідності (логічні пари) складається зі спільного вступного запитання та чотирьох завдань, позначених буквами (або цифрами), до кожного з яких потрібно дібрати один варіант відповіді. Як правило, такі завдання мають 4 основи та 5 - 6 варіантів вибору до них. Завдання на встановлення відповідності різняться за складністю: одні перевіряють тільки знання фактів, формул, правил, інші – розуміння зв’язків між ними. В процесі їх виконання формуються навички порівняння об’єктів, співставлення, представлення об’єктів в різною формі. Вони більш цікаві для учнів видами діяльності, для вчителя – наповненістю змістом. Пропоновані тестові завдання дозволяють за короткий час перевірити об’єм вивченого матеріалу, швидко діагностувати оволодіння учнями основного рівня підготовки з окремих навчальних тем. Дані тести можна використовувати як для індивідуальної перевірки, так і окремими завданнями на самостійних чи контрольних роботах.

Перегляд файлу

Завдання на встановлення відповідності (логічні пари) складається зі спільного вступного запитання та чотирьох завдань, позначених буквами (або цифрами), до кожного з яких потрібно дібрати один варіант відповіді. Як правило, такі завдання мають 4 основи та 5 - 6 варіантів вибору до них.

Завдання на встановлення відповідності різняться за складністю: одні перевіряють тільки знання фактів, формул, правил, інші – розуміння зв’язків між ними. В процесі їх виконання формуються навички порівняння об’єктів, співставлення, представлення об’єктів в різною формі. Вони більш цікаві для учнів видами діяльності, для вчителя – наповненістю змістом.

Пропоновані тестові завдання дозволяють за короткий час перевірити об’єм вивченого матеріалу, швидко діагностувати оволодіння учнями основного рівня підготовки з окремих навчальних тем.

Дані тести можна використовувати як для індивідуальної перевірки, так і окремими завданнями на самостійних чи контрольних роботах.

Алгебра. 7 Клас.

Установіть відповідність між виразами (1 – 4) та їхніми значеннями, якщо 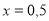(А – Д).

Вираз		Значення виразу
1		А
2		Б
3		В
4		Г
		Д

Для кожного виразу (1 – 4) при 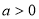доберіть тотожно йому рівний (А – Д).

Вираз		Тотожний вираз
1		А
2		Б
3		В
4		Г
		Д

Установіть відповідність між числовим виразом (1 – 4) та його значенням (А – Д), якщо .

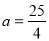Вираз		Значення виразу
1		А
2		Б
3		В
4		Г
		Д

4. Установити відповідність між виразами (1–4) та тотожно рівними їм виразами (А–Д).

1	А	b³
2	Б	b^{– 5}
3	В	b⁷
4	Г	b¹⁰
	Д	b²⁵

Установіть відповідність між виразами (1– 4) і результатами спрощення цих виразів (А-Д).

1	(с²)³: с⁵	А	0
2	с⁷· с³: с⁸	Б	1
3	с¹⁰: (-с⁵)²	В	с²
4	(-с²)³: (с²)²	Г	- с²
		Д	с

Установіть відповідність між виразом (1 – 4) та його числовим значенням (А – Д).

1	А	9
2	Б	3
3	В	27
4	Г	1
	Д	24

Установити відповідність між виразами (1-4) і їх значеннями (А-Д).

1	(-3)²∙4	А	-81
2	3⁴	Б	36
3	0,5∙(-2)⁴+2∙(-0,3)²	В	81
4	ху²∙х, якщо х=2; у=5	Г	8,18
		Д	100

Установити відповідність між виразами (1-4) і їх значеннями (А-Д).

1	(-3)∙(-4)²	А	1000
2	2⁶	Б	11,2
3	0,4∙(-5)²+0,3∙(-2)²	В	-48
4	у³ х³, якщо х=2; у=5	Г	64
		Д	100

Установити відповідність між виразами (1-4) і їх тотожними значеннями (А-Д).

1	5х²-1+3х-4х+5-4х²-4	А	-5x+8
2	(3-2х)-(4х+1)+(6-х)	Б	x-1
3	(х-3)(х+1)	В	x²-x
4	(x-1)²	Г	x²-2x-3
		Д	x²-2x+1

Установити відповідність між виразами (1-4) і їх тотожними значеннями (А-Д).

1	4у²+1-6у-4у-12-4у²	А	2у+3
2	(5у-2)+(4+3у)-(6у-1)	Б	у-1
3	(у+2)(у-1)	В	-10у-11
4	(у+1)²	Г	у²+у-2
		Д	у²+2у+1

Установити відповідність між виразами (1-4) і їх розкладами на множники (А-Д).

1	25х²-10х+1	А	(5-х)(5+х)
2	5х²-10х+5	Б	(х+5)(х2-5х+25)
3	х³+125	В	(х+5)(х2-10х+25)
4	25 -х².	Г	(5х-1)²
		Д	5(х-1)²

Установити відповідність між виразами (1-4) і їх розкладами на множники (А-Д).

1	16х²-8х+1	А	(4х-1)²
2	4х²-8х+4	Б	(х+4)(х2-8х+16)
3	х³+64	В	(х+4)(х2-4х+16)
4	16 -х².	Г	4(х-1)²
		Д	(4-х)(4+х)

Установити відповідність між функціями (1-4) і їх властивостями

(А-Д).

1	у=5х+10	А	Графік функції проходить через початок координат
2	у=0,5х+1	Б	Точка А(2;2) належить графіку функції
3	у=-3х+1	В	Функція є спадною
4	у=3х	Г	х=-2 є нулем функції
		Д	Область визначення функції – всі числа, крім 0

Установити відповідність між функціями (1-4) і їх властивостями (А-Д).

1	у=-4х+1	А	Графік функції проходить через початок координат
2	у=-2х+4	Б	Точка А(1;-3) належить графіку функції
3	у=3х+1	В	Функція є зростаючою
4	у=-8х	Г	х=2 є нулем функції
		Д	Область визначення функції – всі числа, крім 0

Установити відповідність між рівняннями (1-4) і їх розв’язками

(А-Д).

1	2х-4=0 .	А	6
2	0х=0	Б	-6
3	-х=4	В	Безліч коренів
4	0х=5	Г	Рівняння не має розв’язків
		Д	2

Установити відповідність між заданими виразами (1-4) і розкладами цих виразів на множники (А-Д).

1	а³-ав	А	(а-2b)( а²+2аb+4b²)
2	а²-6а+9	Б	а(а²- b)
3	а²-9	В	(а-2b)( а²-2аb+4b²)
4	а³-8b³	Г	(а-3)(а+3)
		Д	(а-3)²

Установіть відповідність між рівняннями (1 –4) та їхніми коренями

(А – Д)

1	А
2	Б	-4
3	В	4
4	Г	12
	Д	3

18. Установіть відповідність між виразами (1 – 4) та їх значеннями (А – Д)


1	А	32
2	Б	8
3	В	64
4	Г	16
	Д	-16

19. Установіть відповідність між виразами (1–4) і тотожно рівними їм виразами (А – Д).

1		А
2		Б
3		В
4		Г
		Д

20.Установіть відповідність між властивостями (1 – 4) функцій і функціями, що мають ці властивості (А – Д).

1	Графік функції проходить через точку	А
2	Графіком функції є горизонтальна пряма	Б
3	Графіку функції належить точка	В
4	Графік функції проходить через початок координат	Г
		Д

21. У завданні установіть відповідність між задачами (1 - 4) і твердженнями (А - Д), які є відповідями до цих задач.

1	Якщо ціну товару збільшили зі 110 до 165 грн, то вона зросла на …	А	20%
2	Якщо ціну товару зменшити зі 150 грн до 105 грн, то вона знизилась на ….	Б	40%
3	Якщо в 150 г розчину міститься 30 г солі, то концентрація солі становить …	В	50%
4	Якщо в 200 г розчину солі міститься 180 г води, то концентрація солі становить…	Г	30%
		Д	10%

23. Установіть відповідність між виразом (1 – 4) та твердженням про його значення (А – Д) при .

Вираз	Твердження про значення виразу
1	А	менше за
2	Б	є простим числом
3	В	є парним
4	Г	ділиться націло на
	Д	ділиться націло на

24. До кожного початку речення (1 – 4) доберіть його закінчення (А – Д) так, щоб утворилося правильне твердження, якщо .

Початок речення		Закінчення речення
1	Значення виразу	А	більше за .
2	Значення виразу	Б	дорівнює .
3	Значення виразу	В	дорівнює .
4	Значення виразу	Г	дорівнює .
		Д	менше за .

25. Установіть відповідність між рівняннями (1 – 4) й числами, які є коренями цих рівнянь (А-Д).

1	-х + 2 = -3	А	-1
2	3х + 4 = - х	Б	- 5
3	2х = 15+5х	В	- 4
4	-3 (2 + х) = 2 – х	Г	5
		Д	4

26. Установіть відповідність між рівняннями (1 – 4) й числами, які є коренями цих рівнянь (А-Д).

1	3х + 4 = -5	А	3
2	– х – 1 = 2 х	Б	2
3	– 5 х = -2 - 4х	В	- 3
4	2 (1 – х) = х – 7	Г	- 2
		Д	-

27. Установіть відповідності між умовами завдань (1-4) і відповідями до них (А-Д). Функцію задано формулою у= -3х + 5. Знайдіть:

1	Значення функції, якщо значення аргументу дорівнює 3	А	7
2	Значення аргументу, якщо значення функції дорівнює -10	Б	2
3	Абсцису точки А(х; -1), яка належить графіку даної функції	В	5
4	Ординату точки А(4; у), яка належить графіку даної функції	Г	-4
		Д	-7

28. Установіть відповідності між умовами завдань (1-4) і відповідями до них (А-Д). Функцію задано формулою у= 5х + 3. Знайдіть:

1	Значення функції, якщо значення аргументу дорівнює -1	А	7
2	Значення аргументу, якщо значення функції дорівнює 13	Б	2
3	Абсцису точки А(х; 8), яка належить графіку даної функції	В	-2
4	Ординату точки А(-2; у), яка належить графіку даної функції	Г	1
		Д	-7

29. Установіть відповідність між рівняннями (1– 4) і їхніми коренями (А-Д).

1	1- (х - 3)² = 0	А	х₁ =-2; х₂ = -4
2	х⁵ - 4 х³ = 0	Б	х = -3
3	(х + 1)³ +8 = 0	В	х = -2
4	х² + 6х + 8 = 0	Г	х₁ =2; х₂ = 4
		Д	х = 0; х = -2; х = 2