Збірник прикладних задач

Про матеріал

Збірник прикладних задач містять задачі геометричного змісту,задачі на рух,задачі на спільну роботу,задачі на собівартість...

Перегляд файлу

ПРИКЛАДНІ ЗАДАЧІ , ЇХ ВИДИ

ТА СПОСОБИ РОЗВ’ЯЗАННЯ

Задача – це сформульоване завдання, відповідь на яке можна знайти за допомогою арифметичних дій.

Етапи розв’язання задачі:

ознайомлення із змістом задачі;
аналіз задачі;
складання плану розв'язання;
розв'язання задачі за планом;
перевірка розв'язування;
запис відповіді.

Схема розв’язання задач

Прочитай умову задачі. Уяви собі задачу як ціле, якомога ясніше не вдаючись до подробиці.
Виясни зміст задачі. Розділи задачу на головні елементи. Зроби схему з головних елементів задачі, розглядаючи їх поодинці, потім співстав із задачею в цілому.
Знайти спосіб розв’язання. Розглянь задачу і знайди її математичну модель, користуючись раніше набутими знаннями.
Розв’язати задачу. Розв’яжи задачу раціональним способом. Переконайся у правильності кожного кроку. Якщо задача дуже важка, то можна поділити її на кілька логічних частин.
Перевірити правильність розв’язання. Перевір розв’язок, а потім підстав знайдені величини в умову.

Способи розв’язування прикладних задач

Існують різні способи розв’язування прикладних задач. Розглянемо деякі з них на конкретних прикладах.

Задача 1. Для туристичного походу 46 школярів підготували шестимісні та чотиримісні човни. Скільки було яких човнів, якщо всі діти помістилися в 10 човнах, вільних місць при цьому не залишилося?

І. Арифметичний спосіб.

Скільки школярів помістилося б у човни, коли б вони були чотиримісними?

4 ∙ 10 = 40 (шк.)

Скільки школярів при цьому не помістилися б?

46 – 40 = 6 (шк.)

Скільки шестимісних човнів було?

6:2=3 (ч.)

Скільки чотиримісних човнів було?

10 – 3 = 7 (ч.)

Відповідь: було 3 шестимісних та 7 чотиримісних човнів.

ІІ. Алгебраїчний спосіб (з допомогою рівняння).

Нехай було х шестимісних човнів, тоді (10 – х) – кількість чотиримісних. У шестимісних човнах поміститься 6х школярів, а в чотиримісних: 4(10 – х) школярів. Всього було 46 школярів.

Складаємо рівняння

6х + 4(10 – х) = 46;

6х + 40 – 4х = 46;

2х = 46 – 40;

2х = 6;

х = 3.

Отже, було 3 шестимісні і 7 = 10 – 3 чотиримісні човни.

ІІІ. Спосіб перебору варіантів.

Так як були човни двох видів, а школярів було 46, то 7 – можлива максимальна кількість шестимісних човнів, тому що 7 ∙ 6 = 42 (шк.), а 9 – максимальна кількість чотиримісних човнів, тому що 9 ∙ 4 = 36 (шк.). Виходячи з цього, складемо таблицю:

К-сть човнів		К-сть школярів		К-сть школярів
6-місних	4-місних	У 6-місних	У 4-місних	К-сть школярів
1	9	6	36	42
2	8	12	32	44
3	7	18	28	46
4	6	24	24	48
5	5	30	20	50
6	4	36	16	52
7	3	42	12	54

З таблиці видно, що задовольняють умову значення 3 човна шестимісних і 7 човнів чотиримісних.

Задача 2. У двох ящиках 53 кг яблук. Скільки яблук у кожному ящику, якщо в першому ящику на 5 кг більше яблук, ніж у другому?

короткий

І. Арифметичний спосіб.

1) 53 – 5 = 48 (кг) – у двох ящиках порівну;

2) 48 : 2 = 24 (кг) – у ящику з меншою масою яблук;

3) 24 + 5 = 29 (кг) – у ящику з більшою масою яблук.

Відповідь: у ящиках 24 кг і 29 кг яблук.

ІІ. Алгебраїчний спосіб.

Нехай у одному ящику х кг яблук, тоді у другому ящику – (х + 5) кг яблук. В обох ящиках 53 кг яблук.

Складаємо рівняння

х + (х + 5) = 53;

2х = 53 – 5;

2х = 48;

х = 48 : 2;

х = 24.

У першому ящику 24 кг яблук; у другому ящику: 24 + 5 = 29 (кг) яблук.

Відповідь: у ящиках 24 кг і 29 кг яблук.

ІІІ. Геометричний спосіб.

Позначимо кількість яблук у ящиках відрізками:

Якщо відрізати частину від довшого відрізка (5 кг), то утворяться 2 відрізки рівної величини. Виходячи з цього: (53 – 5) : 2 = 24 (кг) – відповідає першому відрізку, тоді: 24 + 5 = 29 (кг) – відповідає другому відрізку.

Відповідь: Відповідь: у ящиках 24 кг і 29 кг яблук.

ЗАДАЧІ НА РУХ

Назви та позначення величин: S – відстань (пройдений шлях), t – час

руху, v – швидкість (відстань, пройдена за одиницю часу)

Формули для обчислення величин: S = V ∙ t; V = S : t; t = S : V
Правила обчислення швидкостей та відстані:

Якщо два об’єкти рухаються рівномірно (з постійними швидкостями), то відстань між ними за кожну одиницю часу збільшується або зменшується на однакову кількість одиниць.
Відстань, на яку зближуються об’єкти за одиницю часу, називається *швидкістю зближення*.
Відстань, на яку віддаляються об’єкти за одиницю часу, називається *швидкістю віддалення*.
Правила обчислення швидкостей
Зустрічний рух		Швидкість зближенння:
Рух у протилежному напрямку		Швидкість віддалення:
Рух навздогін		Швидкість зближенння (V₁> V₂):
Рух з відставанням		Швидкість віддалення (V₁< V₂):
Правила обчислення відстані
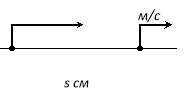
	Зустрічний рух 1) 2) - відстань між об’єктами
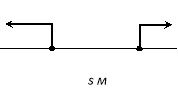
	Рух у протилежному напрямку 1) 2) - відстань між об’єктами
	Рух навздогін 1) 2) - відстань між об’єктами
4)	Рух з відставанням 1) 2) - відстань між об’єктами

Задачі

Скласти задачу за даними таблиці.

Швидкість	Час	Відстань
?	2 год	28 км
?	3 год	210 км
5 км/год	4 год	?
120 км/год	3 год	?
13 км/год	?	26 км
60 км/год	?	240 км
10 км/год	3 год	?
36 км/год	?	72 км
?	год

Із двох пунктів одночасно вийшли два пішоходи. Перший пішохід, що йде зі швидкістю 6 км/год, через 0,5 годин наздогнав другого, який йшов зі швидкістю 4 км/год. Яка відстань між пішоходами була спочатку.

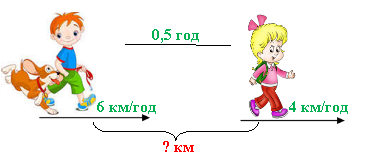Розв’язання:

	*Швидкість, км/год*	*Час, год*	*Відстань, км*
*Перший*	6	0,5	6·0,5
*Другий*	4	0,5	4·0,5

6·0,5=3 (км) – відстань, пройдена першим пішоходом до зустріч;
4·0,5=20 (км) – відстань, пройдена другим пішоходом до зустрічі;
3 – 2=1 (км) – початкова відстань між пішоходом.

Відповідь: спочатку була відстань між пішоходами 1 км.

Одночасно з одного пункту в протилежних напрямках вийшло два пішоходи. Один з них ішов з швидкістю 3км/год. Через дві години пішоходи віддалилися один від одного на 10км. Визнач швидкість другого пішохода.

Розв’язання:

І спосіб (за допомогою рівняння)

Нехай х км/год – швидкість другого пішохода. Тоді перший пішохід за 2 год

пройде 3·2= 6 (км), а другий пішохід пройде 2х км. За умовою задачі вони

пройшли 10 км за 2 год (2х + 6 = 10 км).

Складаємо рівняння.

2х+6=10; 2х=10-6; 2х=4; х=4:2; х=2.

Відповідь: швидкість другого пішохода 2 км/год.

ІІ спосіб

	*Швидкість, км/год*	*Час, год*	*Відстань, км*
*Перший*	3	2	3 · 2
*Другий*	х	2	2х

1) 3 · 2 = 6 (км) – пройшов перший пішохід за 2 год;

2) 10 – 6 = 4 (км) – пройшов другий пішохід за 3год;

3) 4 : 2 = 2 (км/год) – швидкість другого пішохода.

Відповідь: швидкість другого пішохода 2 км/год.

Два мотоцикліста рухаються назустріч один одному. Перший їде зі швидкістю 32км/год, а другий зі швидкістю 38км/год. Зараз між ними 80км. Яка відстань буде між ними через 0,5 годин.

Розв’язання

	*Швидкість, км/год*	*Час, год*	*Відстань, км*
*Перший*	32	0,5	32 · 0,5
*Другий*	38	0,5	38 · 0,5

32 · 0,5=16 (км) – проїхав перший мотоцикліст за 0,5 годин;
38 · 0,5=19 (км) – проїхав другий мотоцикліст за 0,5 годин;
16 + 19=35 (км) – проїхали обидва мотоциклісти за 0,5 години;
80 – 35=45 (км) – така відстань буде між ними через 0,5 години.

Відповідь: 45 км.

Із двох міст, відстань між якими 300 км одночасно виїхали два автомобіля. Зустрілись вони через дві години. Знайти швидкість кожного автомобіля, якщо швидкість першого на 16 км/год більше швидкості другого.

Розв’язання:

	*Швидкість, км/год*	*Час, год*	*Відстань, км*
*Перший*	х + 16	2	300
*Другий*	х	2	300

Нехай х км/год – швидкість другого автомобіля. Тоді (х + 16,5) км/год – швидкість першого автомобіля. За 2 год до зустрічі другий автомобіль проїде 2х км, а 2(х + 16,5) км – проїде перший автомобіль. Всього проїхали 2(х + 16,5) + 2х км, що за умовою дорівнює 300 км.

Складаємо рівняння:

2(х+16)+2х =300;

2х+32+2х=300;

4х+32=300;

4х=300 - 32;

4х=268;

х=268:4

х=67.

Швидкість другого автомобіля 67 км/год, а першого 67+16=83 км/год.

Відповідь: 83 км/год, 68 км/год.

Відстань між двома пристанями 72км. Моторний човен долає цей шлях за течією річки за 3год, а проти течії за 4год. Знайти швидкість течії річки.

Розв’язання:

	*Відстань, км*	*Час, год*	*Швидкість, км/год*
*За течією*	72	3	72:3
*Проти течії*	72	4	72:4

72 : 3 = 24 (км/год) – швидкість катера за течією.
72 : 4 = 18 (км/год) – швидкість катера проти течії.
(24 – 18) : 2 = 6 : 2 = 3 (км/год) – швидкість течії річки.

Відповідь: 3км/год – швидкість течії річки.

Катер ішов по озеру 3 год зі швидкість 21 км/год, а потім 4год за течією річки. Скільки кілометрів подолав катер за 7 год, якщо швидкість течії річки 3 км/год.

Розв’язання :

	*Швидкість, км/год*	*Час, год*	*Відстань, км*
*Озером*	21	3	21 · 3 = 63
*За течією*	21 + 3 = 24	4	24 · 4 = 96

21·3=63 (км) – пройшов катер по озеру;
21+3=24 (км/год) – швидкість катера за течією;
24·4=96 (км) – пройшов катер по річці;
63+96=159 (км) – подолав катер за 7 годин.

Відповідь: 159 км

З пристані Київ до пристані Кременчук вийшов теплохід, і одночасно йому назустріч з пристані Кременчук вийшов катер. Теплохід ішов зі швидкістю 30 км/год, а катер – 24 км/год. Через 5 год вони зустрілися. Яка відстань між пристанями?

Розв’язання:

І спосіб

30 ∙ 5 = 150 (км) – пройшов теплохід за 5 год;
24 ∙ 5 = 120 (км) – пройшов катер за 5 год;
150 + 120 = 270 (км) – відстань між пристанями.

Або: 30 ∙ 5 + 24 ∙ 5 = 270 (км)

ІІ спосіб

30 + 24 = 54 (км/год) – швидкість зближення;
54 ∙ 5 = 270 (км) – відстань, пройдена за 5 год.

Або: (30 + 24) ∙ 5 = 270 (км)

Відповідь: 270 км – відстань між містами.

Мотоцикліст став наздоганяти велосипедиста, коли відстань між ними була 30км. Швидкість мотоцикліста дорівнює 62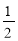км/год, а швидкість велосипедиста на 48км/год менша. Чи наздожене мотоцикліст велосипедиста за год?

Розв’язання :

62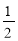∙ = (км) – подолає мотоцикліст за год;
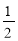(62 – 48) ∙ = 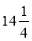∙ = (км) – подолає велосипедист за год;
(км) – відстань, на якій буде мотоцикліст від початкового

положення велосипедиста.

Зобразимо отримані результати:

Отже, мотоцикліст не наздожене велосипедиста.

Складіть і розв’яжіть задачі за таблицями:

	*Швидкість*	*Час*	*Відстань*
*Таксі*	?	4	270
*Автобус*	?	7	560

	*Швидкість*	*Час*	*Відстань*
*Електропотяг*	?	8	720
*Велосипедист*	?	6	108

	*Швидкість*	*Час*	*Відстань*
*Човен*	17	3	?
*Потяг*	54	4	?

Складіть задачі за схемами: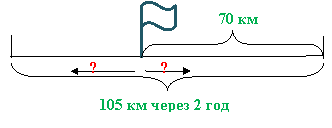

ЗАДАЧІ НА ВИЗНАЧЕННЯ ВРОЖАЙНОСТІ

Середня врожайність – це маса зібраного врожаю із одиниці площі.
Щоб знайти середню врожайність (m), потрібно знайти відношення маси (M) зібраного врожаю до загальної площі (S) полів, на яких вона була вирощена: m = M / S

Задачі

Яка середня врожайність полуниці, якщо зібрали 198 кг з ділянки площею 18 ?

Відповідь: 11кг з 1

$C:\Users\Gigabyte\Desktop\index.jpg$ Який урожай зерна отримає фермер з поля площею 10 га при середній врожайності 35 ц з гектара?

Відповідь: 350 ц

Урожайність ячменю у с. Топильне становить 2/3 урожайності озимої пшениці. Яка урожайність ячменю, якщо озимої пшениці зібрали 54 ц із 2 га Відповідь: 18 ц
Фірма «Агросоюз» у 2014 р. засіяла горохом 80 га поля, що становить 4/5 площі засіяної гречкою. Яку площу засіяли гречкою?

Відповідь: 100 га.

З 12 га зібрали 108 ц гречки, а з 6 га – 72 ц. Знайди середню врожайність гречки на цих ділянках.

Відповідь: 10 ц з гектара

З 7 га першого поля зібрали 145 ц пшениці, а з 8 га другого поля – 185 ц. Яка середня врожайність пшениці з 1 га?

Відповідь: 22 ц з 1 га

Визначте середню врожайність пшениці за рік по таблиці:

Номер поля	Врожайність, т/га	Посівна площа, га
№ 1	3,5	12
№ 2	4,2	8
№ 3	3,1	14

Розв’язання:

3,512 + 4,28 + 3,114 = 119 (т) – масса всього зібраного урожаю;
12 + 8 + 14 = 34 (т) – загальна площа;
119 : 34 = 3,5 (т/га) – середня врожайність пшениці.

Відповідь: 3,5 т/га

На полі площею 26,4 га урожайність проса становила 6,6 ц з 1 га, на поле площею 30,8 га урожайність була 6,3 ц з 1га, а на полі площею 22 га - 7,2 ц з 1 га. Знайдіть середню врожайність проса на всій площі.

Розв’язання:

$C:\Users\Gigabyte\Downloads\1397667933_0px6ufs2rvaq7he.jpg$ 26,46,6 = 174,24 (ц) – зібрали з 1-го поля
30,86,3 = 194,04 (ц) – зібрали з 2-го поля
227,2 = 158,4 (ц) – зібрали з 3-го поля
(174,24 + 194,04 + 158,4) : (26,4 + 30,8 + 22)= = 6,65 (ц) – середня врожайність.

Відповідь: середня врожайність з усього поля становить 6,65 ц з 1 га.

Урожайність багаторічних трав на сіно 15,6 ц з гектара, що становило 0,2 урожайності кукурудзи на силос у 2014 році. Яка урожайність кукурудзи на силос одержала агрофірма у 2014 році?

Розв’язання:

15,6 : 0,2 = 76 (ц)

Відповідь: 76 ц.

Фірмою «Агрос» у 2020 р. озимою пшеницею було засіяно 480 га. Урожайність з 1га становила 25 ц. Державі було продано 80% зібраного врожаю. Решту зерна залишили на потреби фірми. Скільки пшениці залишили на потреби фірми?

480 25 0,8 – = 12000 (ц) – зібрали всього пшениці;
12000 0,8 = 9600 (ц) – продали державі;
1200 – 9600 = 2400 (ц) – залишилося на потреби фірми.

Відповідь: 2400 ц

ВАРТІСТЬ ПОКУПКИ, ЦІНА ТА КІЛЬКІСТЬ ТОВАРУ

Ціна товару дорівнює вартості покупки, поділеній на кількість (масу) товару.
Вартість покупки – ціна, помножена на кількість одиниць товару.
Кількість товарів дорівнює вартості покупки, поділеній на ціну одиниці товару.

Задачі

У коморі було 350 кг цукру. За зиму витратили 6/7 усього цукру. Скільки кілограмів цукру витратили за зиму?

Відповідь: 300 кг.

У магазині було 420 телевізорів, 1/7 всіх телевізорів продали. На скільки менше телевізорів продали, ніж залишилося?

Розв’язання:

(т.) – продали;
420 – 60 = 360 (т.) – залишилося;
360 – 60 = 300 (т.) – на скільки менше продали, ніж залишилося.

Відповідь: на 300 телевізорів.

До магазину привезли 81 кг яблук і 54 кг груш. На скільки більше ящиків яблук привезли, якщо у 1 ящику вміщується 9 кг груш, або 9 кг яблук?

Відповідь: на 3 ящики яблук більше.

Мама заплатила за 5 кг картоплі 35 грн., а за 3 кг апельсинів 48 грн. Що дорожче, 1 кг апельсинів чи 1 кг картоплі і на скільки?

Відповідь: 1 кг апельсинів дорожчий за 1 кг картоплі на 9 грн.

Печиво коштує 28 грн. скільки буде коштувати 1,5 кг цього печива?

Відповідь: 42 грн.

1 кг пряників коштує грн. Скільки коштують а) 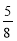кг; б)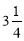кг пряників?

Розв’язання:

а) = 3,5 (грн)

б) = (грн)

Відповідь: кг коштують 3,5 грн.; кг коштують грн.

Змішали 4, сорти цукерок за ціною 7,5 грн.; 8,4 грн., 9,5 грн., 10,6 грн. Скільки коштує 1 кг суміші, якщо взяли:

а) кожного сорту цукерок по 1 кг;

б) цукерок 1 і 3 сорту — по 2 кг; цукерок 2 і 4 сорту — по 1 кг?

Розв’язання:

7,5 + 8,4 + 9,5 + 10,6 = 36 (грн);
7,5 ∙ 2 + 9,5 ∙ 2 + 8,4 + 10,6 = 53 (грн).

Відповідь: а) 36 грн; б) 53 грн.

Для класу купили зошити, ручки та олівці. Вартість зошитів становила 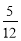вартості всієї покупки, вартість ручок — 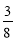, а вартість олівців — 70 гривень. Знайти вартість покупки.

Розв’язання:

1) – таку частину вартості всієї покупки становить вартість ручок і

зошитів.

2) – таку частину вартості всієї покупки становить вартість олівців.

3) (грн) – вартість покупки.

Відповідь: вартість покупки – 336 гривень.

Для новорічних подарунків купили цукерки. Вартість шоколадних цукерок становить 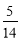вартості всієї покупки, вартість карамельок — решти грошей. Крім цього купили на 33 грн. мармеладок. Скільки всього потратили грошей на подарунки?

Розв’язання:

– становить вартість карамельок і жувальних цукерок від вартості всієї покупки;
– становить вартість карамельок від загальної вартості покупки;
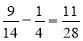– частина від загальної вартості, яку становить вартість жувальних цукерок4
(грн.) – загальна вартість подарунка.

Відповідь: 84 грн.

За 33 м тканини і 20 м клейонки заплатили 882 грн. Вартість тканини становила вартості клейонки. На скільки дорожчий: 1м тканини чи 1м клейонки?

Розв’язання:

Ціна за 1 м, грн.

Кількість, м

Вартість, грн.

Тканина

882 грн.

Клейонка

Нехай 1 м клейонки коштує х грн., тоді 1 м тканини буде коштувати х грн. За 33 м тканини заплатили: (грн.), а за 20 м клейонки заплатили 20х грн., всього заплатили 882 грн.

Складаємо рівняння

22х + 20х = 882;

42х = 882;

х = 882 : 42;

х = 21.

Ціна клейонки: 21 грн.;

Ціна тканини: (грн.)

Дізнаємося, на скільки дорожчий 1 м клейонки: 21 – 14 = 7 (грн.)

Відповідь: 1 м клейонки дорожчий, ніж 1 м тканини на 7 грн.

Ціна товару після збільшення на 20% стала 168 грн. Якою була початкова ціна?

Розв’язання:

100%+20%=120% – нова ціна у відсотках;
168:1,2= 140(грн) – початкова ціна
- Ціна товару спочатку знизилася на 15%, потім збільшилася на 15%. Чи змінилася ціна товару?

Розв ’язання:

Нехай а грн. – початкова ціна товару. Після першої зміни (збільшення) вона стала: 1,15а грн. А після другої зміни (зменшення) нова ціна стала:

1,15а ∙ 0,85 = 0,9775а (грн), що становить 97, 75% від початкової. Початкова ціна: 100% - 97,75% = 2,25%.

Відповідь: ціна зменшилася на 2,25%.

Товар продавався за ціною 140 грн, після збільшення ціна стала дорівнювати 168 грн. На скільки відсотків збільшилася ціна?

(168 : 140) ∙ 100% = 120% – нова ціна у %;
120% – 100%= 20% – на стільки збільшилася початкова ціна.

Відповідь: ціна збільшилася на 20%.

ЗАДАЧІ, ПОВ’ЯЗАНІ З ГОСПОДАРСЬКОЮ

ДІЯЛЬНІСТЮ ЛЮДИНИ

$C:\Users\Gigabyte\Desktop\1329208068_u0acrj8pkzy3mve.jpeg$ Господар мав вивезти з городу 49 ц картоплі. Першого дня він вивіз 2/7 усієї картоплі, а другого дня – 1/5 тієї картоплі, що залишилася. Скільки центнерів картоплі вивіз господар другого дня?

Розв’язання

(ц) – вивіз господар першого дня;
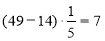(ц) – вивіз господар другого дня.

Відповідь: 7 центнерів.

Господиня спекла 2 калачі: маса першого – 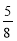кг, а другого – 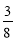кг. На скільки перший калач важчий від другого?

Відповідь: на кг.

У 6 лотках на 40 яєць більше, ніж у 4 таких лотках. Скільки яєць в усіх лотках разом?

Розв’язання:

40 яєць знаходиться у 2 лотках (6 – 4 = 2), тому у 1 лотку 20 яєць. Всього

яєць у 10 лотках.

Відповідь: 200 яєць.

На деякій ділянці залізничного шляху старі рейки завдовжки 6 м вирішили замінити новими завдовжки 9 м. Скільки потрібно нових рейок, щоб замінити 720 старих рейок?

Розв’язання:

І спосіб: (шт.) – потрібно нових рейок.

ІІ спосіб.

Складемо пропорцію:

; .

Відповідь: потрібно замінити 720 старих рейок на 480 нових.

*Довжина рейок, м*		*Кількість рейок, шт.*
9	–	х
6	–	720
Величини обернено пропорційні

При відгодівлі великої рогатої худоби 40 кг сіна можна замінити 25 кг силосу. Скільки потрібно силосу, щоб замінити 552 кг сіна?

Розв’язання:

І спосіб: (кг) – потрібно силосу.

ІІ спосіб:

Маса сіна, кг		Маса силосу, кг
40	–	25
552	–	х
Величини прямо пропорційні

Складемо пропорцію:

;

Відповідь: потрібно 345 кг силосу для заміни 552 кг сіна.

У фермерському господарстві господарстві на поливних землях збирали з гектара 60,8 ц пшениці. Заміна старого сорту пшениці новим дає збільшення врожаю на . Скільки тепер пшениці збирають у господарстві з 23 га поливного поля? Розв’яжіть задачу кількома способами.

Розв’язання:

І спосіб

1398,4 (ц) – збирали раніше;
1398,4 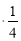+ 1398,4 = 1748 (ц) – збирають тепер.

ІІ спосіб

(ц).

Відповідь: 1748 ц пшениці збирають тепер.

Три трактористи зорали 132,4 га землі, причому перший з них зорав у 1,1 рази більше з другого, а третій – у 1,1 рази менше від другого. Яку площу зорав кожен тракторист?

Розв’язання:

І тракторист

у 1,1 рази ˃

(га)

ІІ тракторист

1,1х (га)

ІІІ тракторист

у 1,1 рази ˂

х (га)

Складемо рівняння

1,21х + 1,1х +х = 132,4;

3,21х = 132,4;

х = 132,4: 3,31;

х = 40 (га) – зорав ІІІ тракторист;

(га) – зорав ІІ тракторист;

(га) – зорав І тракторист.

Відповідь: трактористи зорали відповідно 48,4 га, 44 га, 40 га землі.

У магазині після обіду продали 39 кг 600 г цукерок, що становить 1/3 всієї кількості цукерок, проданої до обіду. Після цього у магазині залишилося 68 кг 450 г цукерок. Визнач масу цукерок, яка була в магазині спочатку.

Розв’язання:

Було спочатку

Продали

Залишилося

Після обіду: 39 кг 600 г =

= 39,6 кг, що становить

68 кг 450 г =

= 68,45 кг

До обіду: х кг

Нехай до обіду продали х кг цукерок, тоді:

х = 39,6 : 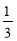= 118,8 (кг) – продали до обіду;
39,6 + 118,8 + 68,45 = 226,85 (кг) – було спочатку.

Відповідь: у магазині було 226,85 кг цукерок.

ЗАДАЧІ ГЕОМЕТРИЧНОГО ЗМІСТУ

Формули для знаходження величин площі та об’єму:

, ;

Залежність між одиницями вимірювання лінійних розмірів, площі, об’єму.
Властивості прямо та обернено пропорційних величин.

Задачі

Встановіть відповідність між термінами першого та другого стовпчиків:

Прямокутник
Квадрат
Куб
Прямокутний паралелепіпед

Фігури, зображені на рисунку, складено з кубиків з ребром 1 см. Знайдіть об’єм кожної фігури.

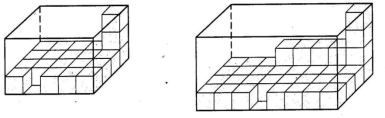
Відповідь. 21 см³; 38 см³.

Розчистили від снігу ковзанки, що становить 800 . Знайдіть площу ковзанки.

Розв’язання: () – площа ковзанки.

Відповідь: площа ковзанки 2000.

Дві ділянки прямокутної форми мають однакову площу. Довжина однієї ділянки 8 м, а ширина 4,5 м. Знайдіть довжину другої ділянки, якщо її ширина дорівнює 2 м.

Розв’язання:

І спосіб

– площа першої ділянки;
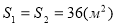– площі обох ділянок рівні за умовою задачі;
36 : 2 =18 (м) – довжина другої ділянки.

ІІ спосіб

	Довжина ділянок, м	Ширина ділянок, м	Площа ділянок,
Перша ділянка	8	4,5
Друга ділянка	х	2
	Величини обернено пропорційні

Складемо пропорцію:

;

Відповідь: 18 метрів – довжина другої ділянки.

Довжина підлоги 5 м, ширина – 4 м. Скільки треба прямокутних плиток розмірами 20 см на 25 см, щоб вистелити ними підлогу?

Розв’язання

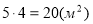= 200000 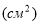– площа підлоги;
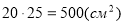– площа однієї плитки;
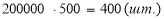– потрібно плиток.
- Для того, щоб побудувати стіну завдовжки 18 м, завтовшки 0,5 м і заввишки 3м, потрібно 10800 цеглин. Якої висоти стіну можна побудувати при довжині 15 м, товщині 0,25 м, маючи 5400 таких цеглин?

Розв’язання:

	*Кількість цеглин, шт.*	*Об’єм стіни,*	*Об’єм стін*
*Перша Стіна*	10800
*Друга стіна*	5400
	Величини прямо пропорційні

І спосіб:

Складаємо пропорцію

;

х = 3,6 (м)

ІІ спосіб:

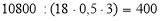(шт.) – цеглин на 1;
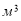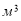() – об’єм стіни, яку можна побудувати із 5400 цеглин;
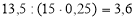(м) – висота нової стіни.

Відповідь: висота стіни із 5400 цеглин становить 3,6 метрів.

ЧИТАННЯ ТА ПОБУДОВА ДІАГРАМ, ГРАФІКІВ

В овочесховищі 70% місткості зайнято картоплею, – капустою, а решта – морквою. Побудуйте:

а) Кругову діаграму;

б) Стовпчасту діаграму (гістограму).

Розв’язання:

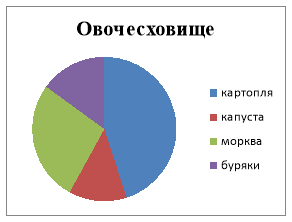Кругова діаграма: Стовпчаста діаграма:

Побудуй кругову та стовпчасту діаграму розподілу часу протягом дня для учня 6 класу, якщо на сон він витрачає 9 годин, на навчання – 7 годин, на заняття в гуртках – 2 години, вільний час – 6 годин.

Розв’язання:

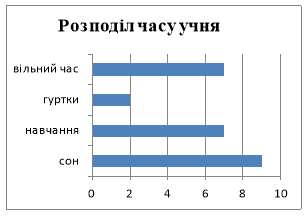
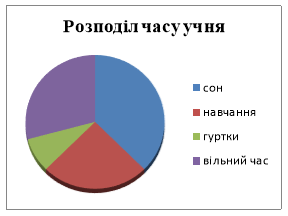Кругова діаграма: Стовпчаста діаграма:

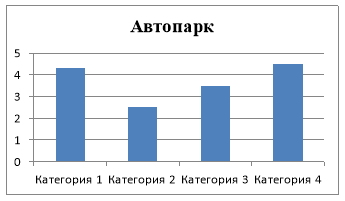
У автопарку налічується 120 вантажних автомобілів. З них: КАМАЗ (К) - 40, ЗИЛ (З) - 25, МАЗ (М) – 35, інші ГАЗ (Г).

За даними задачі складіть таблицю та побудуйте гістограму.

Розв’язання:

*Назва* *вантажівок*	*Кількість*
КАМАЗ	40
ЗИЛ	25
МАЗ	35
ГАЗ	– 100 = 20

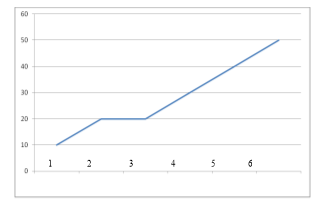На малюнку зображено таблиця та графік руху велосипедиста:

*Тривалість* *руху, год*	*Відстань, км*
1	10
2	20
3	20
4	30
5	40
6	50

Користуючись графіком, дайте відповіді на запитання:

а) Який час був в дорозі велосипедист?

б) Яку відстань проїхав велосипедист за 2 год; за 4 год?

в) З якою швидкістю він їхав?

г) Чому не змінювалася відстань з 2 по 3години руху?

д) Яку відстань проїхав велосипедист за 6 год?

За таблицею побудовано графік зміни температури протягом доби.

Час, год	2	4	6	8	10	12	14	16	18	20	22	24
Температура, ̊С	1	0	-2	-3	-1	1	4	5	6	5	4	3

Користуючись графіком, дайте відповіді на запитання:

а) Якою була температура повітря о 4 годині; о 22 годині?

б) О котрій годині температура була найвищою; найнижчою?

в) О котрій годині температура була нульовою?

г) У який час доби температура була вище нуля; нижче нуля?

д) У який час доби температура спадала; зростала?

е) О котрій годині температура була 1 ̊С; -1 ̊С?

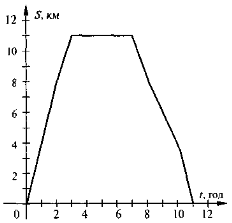На рисунку зображено графік руху туристів. Розглянувши графік, дайте відповідь на запитання:

а) На якій відстані був турист через 2 години після виходу з дому?

б) Скільки часу турист витратив на зупинку?

в) Через скільки годин після виходу турист був на відстані 4 км від дому?

г) з якою швидкістю туристи рухались перші 2

год?

д) З якою швидкістю туристи повертались додому?

На рисунку зображено графік руху групи туристів.

Дайте відповіді на запитання:

а) На якій відстані від початку шляху були туристи через t годин, якщо

t = 1; 1,5; 3; 3,5; 7; 9,5?

б) Скільки часу знадобилось туристам, щоб прибути в пункт призначення, що заходиться на відстані S км, якщо S = 2; 9; 10; 16; 18?

в) Чому дорівнює початкова швидкість туристів і як довго вони рухались із такою швидкістю?

г) Чому дорівнювала швидкість туристів протягом третьої години руху?

д) Через скільки годин після початку руху туристи зробили першу зупинку і як довго вони відпочивали?

е) З якою швидкістю рухалися туристи після першої зупинки і скільки кілометрів рухались вони з цією швидкістю?

є) З якою швидкістю рухалися туристи після другої зупинки і коли вони прибули до місця призначення?

ж) З якою середньою швидкістю рухалися туристи, тобто скільки кілометрів проходили б вони щогодини, якщо б не було зупинок і швидкість протягом усього шляху була б сталою?

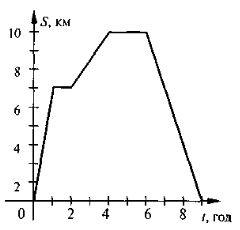Складіть задачу за графіком руху.

ЕЛЕМЕНТИ СТАТИСТИКИ, КОМБІНАТОРИКИ

ТА ТЕОРІЇ ЙМОВІРНОСТЕЙ

Правило суми. Якщо об'єкт A можна вибрати m способами, а об'єкт B – n іншими способами, то вибір "або A, або B" можна здійснити m + n способами.

Павило добутку. Якщо об'єкт A можна вибрати m способами і після кожного такого вибору об'єкт B може бути вибраним n способами, то вибір "A і B" в указаному порядку можна здійснити m ∙ n способами.

Види подій: випадкові; неможливі; достовірні.

Граф – «дерево» можливих варіантів.

Ймовірність випадкової події: , де Р(А) — ймовірність події А, m — кількість сприятливих випробувань (коли подія А настала), n — кількість усіх випробувань.

Задачі

Чи можна стверджувати, що в класі напевно знайдуться хоча б два учні з однаковими датами народження, якщо в школі: а) 320 учнів (не завжди): б) 500 учнів (можливо)?
Із 17 троянд, 8 волошок і 9 ромашок складено букет. Чи є в цьому букеті троянди, якщо букет містить: а) 17 квіток (можливо); б) 20 квіток (так)?
Економіст, аналізуючи тарифні розряди одного з цехів заводу вибрав 10 робітників і виписав їх тарифні розряди: 4, 5, 7, 4, 6, 5, 6, 4, 4, 5. Складіть за цими даними статистичний ряд. Виберіть правильну відповідь і встановіть, який розряд зустрічається найчастіше?

а) 5,5,6,7; б) 1,2,3,4; в) 7,6,5,4; г) 4∙4; 5∙3; 6∙2; 7; д) 4,4,4,4,5,5,5,6,6,7.

Група учнів з 10 осіб підтягувалися на перекладині. Результати підтягування були такими: 12,10,9,10,10,11,11,8,9,7. Складіть таблицю кількості підтягувань із даних результатів. Знайдіть середнє значення підтягувань учнів.
Є 5 червоних троянд і 7 білих. Скільки існує варіантів вибору однієї квітки?

Розв’язання:

За правилом суми: 5 + 7 = 12 варіантів вибору.

У коробці є 6 кольорових олівців і 7 фломастерів. Скількома способами можна вибрати один олівець або один фломастер?

Розв’язання:

За правилом суми: 6 + 7 = 13 способів.

У коробці є 5 олівців і 7 фломастерів. Скількома способами можна вибрати пару, яка складається із одного олівця і одного фломастера?

Розв’язання:

За правилом добутку: 5 ∙ 7 = 35 способів.

У групі 10 дівчаток і 15 хлопчиків. Скількома способами із цієї групи можна вибрати: а) одного хлопчика; б)одного хлопчика або одну дівчинку; в) одного хлопчика і одну дівчинку?

Розв’язання:

а) Із 15 хлопчиків одного можна вибрати 15 способами;

б) за правилом суми дівчинку або хлопчика можна вибрати: 10 + 15 = 25 способами.

в) за правилом добутку пари «дівчинка і хлопчик» можна вибрати: 10 ∙ 15 = 150 способами.

Відповідь: а) 15; б) 25; в) 150 способів.

Четверо друзів народилися в один день, тому кожного року вони обмінюються подарунками. Скільки всього подарунків дарять хлопці?

Розв’язання:

За правилом добутку: 4 ∙ 3 = 12 подарунків.

В магазині "Все до чаю" є 5 різних чашок та 3 різних блюдця. Скількома способами можна купити чашку з блюдцем?

Розв’язання:

Виберемо чашку. У комплекті з нею можна вибрати будь-яке з трьох блюдець. Тому є три різні комплекти, які мають вибрану чашку. За правилом добутку: 5 ∙ 3 = 15 способів.

В магазині "Все до чаю" є 5 різних чашок та 3 різних блюдця та 4 чайні ложки. Скількома способами можна купити комплект з чашки, блюдця та ложки?

Розв’язання:

За правилом добутку: 5 ∙ 3 ∙ 4 = 60 способів.

В магазині "Все до чаю", продається 5 чашок, 3 блюдця та 4 чайні ложки. Скількома Скільки існує можливих варіантів, щоб купити два предмети з різними назвами?

Розв’язання:

Можна купити три різні комплекти: перший – чашка з блюдцем (5 ∙ 3 = 15 варіантів); другий – чашка з ложкою (5 ∙ 4 = 20 варіантів, третій – блюдце та

ложка (4 ∙ 3 = 12 варіантів). Тому: 15 + 20 + 12 = 47 варіантів.

Відповідь: є 47 варіантів.

Скількома способами можна обрати президента та віце-президента фірми із 5 членів правління?

Розв’язання:

Якщо обирається президент із 5 членів правління, то віце-президент буде обиратися із 4 членів правління, тому за правилом добутку: 5 ∙ 4 = 20 способів.

Відповідь: 20 способами.

Запишіть усі трицифрові числа цифрами 1, 2, 3 без повторень. Скільки таких чисел можна записати?

Розв’язання:

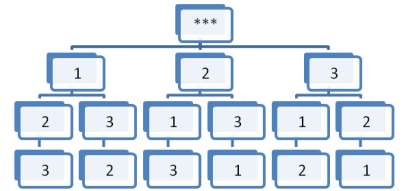Позначимо можливі трицифрові числа *** і зобразимо їх у вигляді графа.

Отримали числа: 123, 132, 213, 231, 312, 321. Із цієї схеми бачимо, що таких

чисел може бути 6.

Четверо гравців команди повинні взяти участь у турнірі з шашок так, щоб кожен зіграв з кожним одну партію. Скільки всього партій буде зіграно.

Розв’язання:

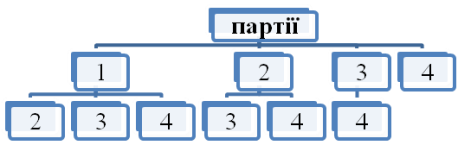Позначимо гравців номерами 1, 2, 3, 4. Бачимо, що перший гравець зіграє три партії, другий дві (без першого); третій одну партію (без першого і другого); четвертий жодної, тому що він вже зіграв зі всіма гравцями. Тому буде зіграно 6 партій.

Віслюк Іа має три надувні кульки: червону, зелену та жовту. Він хоче подарувати по одній кульці своїм друзям: Вінні-Пуху, П’ятачку і Кролику. Скількома варіантами він може це зробити?

*Можливі варіанти*	*Вінні-Пух*	*П’ятачок*	*Кролик*
1	Червона	Зелена	Жовта
2	Червона	Жовта	Зелена
3	Зелена	Жовта	Червона
4	Зелена	Червона	Жовта
5	Жовта	Зелена	Червона
6	Жовта	Червона	Зелена

Розв’язання:

За таблицею видно, що таких варіантів є 6.

Відповідь: 6 варіантів.

Чотири подруги купили чотири білети в кінотеатр. Скількома різними способами вони можуть сісти на свої місця в глядацькому залі?

Розв’язання:

У першої подруги є можливість сісти на одне із 4-х місць, у другої – на одне із 3-х місць, що залишились після першої, у третьої – на одне із двох місць, а в четвертої – одне вільне місце. Тому 4 ∙ 3 ∙ 2 ∙ 1 = 24 способів.

Яка ймовірність того, що навмання вирваний з нового календаря аркуш відповідає 30-му числу, якщо в році 365 днів?

Розв'язання:

Оскільки в році 365 днів, у календарі 365 аркушів, вириваємо один навмання, то рівні шанси є вирвати будь-який з цих 365 аркушів; тому я = 365. У році 12 місяців, але тільки в 11 є 30-е число (виняток — лютий), тому аркушів, що задовольняють умову всього 11, отже, т = 11. Маємо: Р ==.

З 25 екзаменаційних білетів, що пронумеровані числами від 1 до 25, навмання обирають один. Яка ймовірність того, що номер витягнутого білета є число, що кратне трьом?

Розв’язання:

Числа, кратні числу 3 від 1 до 25: 3,6,9,12,15,18,21,24. Їхня кількість – 8.

Маємо: Р ==.

У їдальні на обід є 2 перші страви, 3 другі і 3 треті. Ви замовляєте обід собі і своєму товаришеві. Яка ймовірність того, що ви вгадаєте бажання товариша.

Розв’язання:

Знайдемо загальну кількість можливого замовлення обіду за правилом добутку: 2 ∙ 3 ∙ 3 = 18.

Тому маємо: Р ==.

ВІДСОТКОВІ РОЗРАХУНКИ.

ЗАДАЧІ ЕКОНОМІЧНОГО ЗМІСТУ

Основні правила відсоткових розрахунків:

р% від А→;
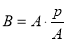В – р% →;
А збільшено на р% →;
А зменшено на р% →.

Задачі

Дим від однієї цигарки містить 5 мг нікотину. Скільки нікотину за один день попаде в організм людини, яка спалює 15 цигарок, якщо від кожної цигарки поглинається 20% нікотину?

Розв’язання:

1)(мг) – вміст нікотину у 15 цигарках;

2) (мг) – нікотину попаде в організм людини.

Відповідь: 15 мг нікотину.

Визначте вміст у відсотках самих шкідливих речовин, що містить тютюновий дим (синильної кислоти, тютюнового дьогтю, окису вуглеводів, полонію) в одній цигарці, якщо нікотину міститься 2%, а синильна кислота становить 1/2 частини нікотину, тютюнового дьогтю в 7,5 разів більше, ніж нікотину, окис вуглеводів становить 3/5 від кількості тютюнового дьогтю, полонію міститься 2/3 від кількості окису вуглеводу.

Розв’язання: 1) – синильна кислота;

2) – дьоготь;

3) – окис вуглеводів;

4) – полоній.

Відповідь: 1%, 15%, 9%, 6%.

Середня вага новонародженої дитини становить 3кг 300г. Коли мати дитини під час вагітності палить, то ця вага зменшується на 300г, коли палить батько, то вага зменшується на 125г. Визначте , скільки відсотків втрачає при народженні дитина, якщо: а) мати палить; б) батько палить; в) палять мати і батько. Відповідь округліть до одиниць.

Розв’язання:

а) – втрачає новонароджена дитина, коли палить мати;

б) – втрачає новонароджена дитина, коли палить батько;

в) – втрачає новонароджена дитина.

Один кВт/год електроенергії коштує 1,46 грн. Якщо кожен із 4 членів сім’ї збереже 10% електроенергії при умові, що за місяць сім’я споживає 150 квт, то скільки гривень буде заощаджено за місяць?

Розв’язання

(150 ∙ 0,1) ∙ 1,46 = 21,9 (грн.) – заощадить кожен член родини за місяць;

21,9 ∙ 4 = 87,6 (грн.) – заощадить вся сім’я за місяць.

Відповідь: за місяць сім’я заощадить 87, 6 грн.

У кімнаті, де за батареями опалення на стіні наклеєний теплоізоляційний матеріал, зберігається тепла на 5% більше. На 1 кв. м кімнати припадає 1,32 Ккал тепла. Скільки тепла збережеться у кімнаті площею 17 кв.м, якщо утеплити стіну?

Розв’язання:

1,32 ∙ 17 = 22,44 (Ккал) – припадає тепла на всю кімнату;

22,44 ∙ 0,05 = 1,122 (Ккал) – економія тепла.

Відповідь: при теплоізоляції стін буде зекономлено 1,122 Ккал тепла.

За місяць бригада робітників заасфальтувати 88,4 км дороги, що становило 104% плану. Скільки кілометрів дороги треба було заасфальтувати за планом?

Розв’язання

І спосіб

88,4 : 1,04 = 85 (км) – за планом.

ІІ спосіб

88,4 км – 104%

х км – 100%

Складаємо пропорцію:

;

Відповідь: за планом потрібно було заасфальтувати 85 км дороги.

За місяць кондитерська фабрика виготовила продукції на 453 тис. грн, що було на 25% більше, ніж заплановано. На яку суму планували на фабриці виготовити продукцію?

Розв’язання

453 тис. грн – 125%

х тис. грн – 100%

Складаємо пропорцію:

;

Відповідь: на 362,4 тис. грн планували виготовити продукції.

На скільки відсотків знизилась вартість товару, якщо він коштував 200 грн, а тепер коштує 185 грн?

Розв’язання

І спосіб

185 : 200 ∙ 100 = 92,5% становить нова вартість товару;
100 – 9,5 % = 7,5% – відсоток зниження вартості.

ІІ спосіб

*Початкова ціна, грн*		*Початкова ціна, %*
200	–	100
185	–	х
Величини прямо пропорційні

Складаємо пропорцію:

; ; х = 92,5%; 100 – 92,5 = 7,5%

Відповідь: вартість товару знизилась на 7,5%.

Ціна на залізничний квиток коштує 120 грн. Її підвищили на 10 %. Якою стала ціна квитка? (132 грн)

Розв’язання

120 + 120 ∙ 0,1 = 132 (грн)

Відповідь: квиток став коштувати 132 грн.

Маса ящика з товаром 11,5 кг. Маса товару 9,2 кг. Скільки відсотків становить маса порожнього ящика від маси з товаром?

Розв’язання:

1)Яка маса порожнього ящика?

11,5 – 9,2 = 2,3 (кг)

2)Скільки відсотків становить маса порожнього ящика від маси з товаром?

2,3 : 11,5 ∙ 100 = 20%

Відповідь: маса порожнього ящика від маси з товаром становить 20%.

Фермер зібрав 18 т зернових, із них 4,5 т кукурудзи. Скільки відсотків становить маса зібраної кукурудзи від маси зернових?

Розв’язання

4,5 : 18 ∙ 100 = 25%

Відповідь: маса зібраної кукурудзи від маси зернових становить 25%.

Автомобіль «Славута» коштує 40 000 грн. Банк дає кредит на купівлю автомобіля за умовою першого внеску 25% від загальної суми та з подальшою виплатою коштів протягом двох років під 12% річних. Скільки треба буде сплачувати грошей у банк кожного місяця.

Розв’язання

Знайдемо 25 % від 40 000 – перший внесок:

40 000 ∙ 0,25 = 10 000 (грн) ;

Знайдемо залишок від загальної суми:

40 000 – 10000 = 30 000 (грн)

Нараховуємо відсотки банку, тобто 12 % від 30 000 грн:

30 000 ∙ 0,12 = 3600 (грн)

Загальна сума, що залишається для оплати протягом років:

30 000 + 3600 = 36 600 (грн)

Кожного місяця слід сплачувати:

36 600 : 24 = 1525 (грн).

Відповідь: кожного місяця треба сплачувати 1525 грн.

Авансом робітник отримав 84 гривні, що складає 7% його заробітної плати. Визначити розмір всієї заробітної плати робітника.

Розв’язання

0,07 = 1200 (грн)

Відповідь: 1200 грн – розмір заробітної плати робітника.

Скільки грошей буде у клієнта банку на рахунку через рік від суми вкладу 100 грн, якщо банк виплачує 25% річних.

Розв’язання

100 + 100 ∙ 0,25 = 125 (грн)

Відповідь: на рахунку буде через рік 125 грн.

Банк сплачує 25% річних. Скільки одержить клієнт прибутку через один рік, якщо поклав у банк 220 грн?

Розв’язання

І спосіб

220 ∙ 0,25 = 55 (грн)

ІІ спосіб

*Початкова ціна, грн*		*Початкова ціна, %*
220	–	100
х	–	25
Величини прямо пропорційні

Складемо пропорцію:

Відповідь: 55 грн одержить клієнт прибутку.

Агрофірма поклала у банк 200 000 грн. За перший рік їй було нараховано 20 000 грн. За другий рік банківський відсоток було зменшено на 2%. Яка сума стала в банку через 2 роки?

Розв’язання

Знайдемо відсоток нарахувань за перший рік:

Початкова ціна, грн		Початкова ціна, %
200000	–	100
20000	–	х
Величини прямо пропорційні

Складемо пропорцію:

;

% – відсоток за перший рік;

20 % - 2 % = 18% – відсоток за другий рік;

(200000 + 20000) ∙ 0,18 = 39600 (грн) – прибуток за другий рік;

200000 + 39600 = 239600 (грн) – сума на рахунку через 2 роки.

Відповідь: 239600 грн.

Сплав складається з 50% міді, 40% цинку і 10% алюмінію.
Скільки треба взяти металів, щоб дістати 35 кг сплаву?

Розв’язання

35 : 100 = 0,35 (кг) – містить 1% сплаву;
0,35 ∙ 50 = 17,5 (кг) – мідь;
0,35 ∙ 40 = 14 (кг) – цинк;
0,35 ∙ 10 = 3,5 (кг) – алюміній.

Відповідь: потрібно взяти 17,5 кг міді, 14 кг цинку; 3,5 кг алюмінію.

Є два сплави міді зі сріблом. Перший сплав містить 85% срібла, а другий — 60%. Шматок першого сплаву масою 4 кг сплавили зі шматком другого сплаву масою 6 кг і одержали третій сплав. Знайдіть у відсотках вміст срібла у третьому сплаві.

Розв’язання

	*Маса сплаву, кг*	*Маса срібла, %*	*Маса срібла, кг*
І сплав	4	85	4 ∙ 0,85 = 3,4
ІІ сплав	6	60	6 ∙ 0,6 = 3,6
ІІІ сплав	4 + 6 = 10	х	3,4 + 3,6 = 7

Знайдемо відсоткове відношення маси срібла до маси сплаву:

Відповідь: вміст срібла у сплаві становить 70%.

Маємо 735 г 16 % розчину йоду у спирті. Треба дістати 10 % розчин
йоду. Скільки грамів спирту треба долити для цього у даний розчин?

Розв’язання:

І спосіб

735 ∙ 0,16 = 117,6 (г) – йоду у 16% розчині;
117,6 : 0,1 = 1176 (г) – маса 10% розчину;
1176 – 735 = 441 (г) – треба долити спирту.

*Маса розчину, г*	*Вміст йоду, %*
735	16
х	10
Величини обернено пропорційні

ІІ спосіб

Складаємо пропорцію

;

(г) – маса 10% розчину.

Знайдемо масу спирту, який треба долити до 735 г:

1176 – 735 = 441 (г)

Відповідь: потрібно долити 441 г спирту, щоб дістати 10% розчин йоду.

ЗАДАЧІ НА ВИКОНАНУ РОБОТУ

Продуктивність праці (N)– кількість роботи (А), зробленої за одиницю часу (t);
Основні формули: N = А/ t, А = N ∙ t; t = А/ N;

Задачі

Перша друкарка за 6 год друкує 24 сторінки, а друга за 8 годин - 40 сторінок. За скільки годин спільної роботи ці друкарки надрукують 252 сторінки?

Розв’язання:

	*К-сть сторінок*	*Час виконання роботи*	*Продуктивність* *за 1 годину*
І друкарка	24	6	24 : 6 = 4
ІІ друкарка	40	8	40 : 8 = 5
Разом	252	?	4 + 5 = 9

Працюючи разом, друкарки надрукують 252 сторінки за 252 : 9 = 28 год

Відповідь: за 28 год.

Перший насос викачує 960 відер води за 32 хв, а другий - за 48 хв. За скільки хвилин ці насоси викачають 1000 відер води, якщо працюватимуть разом?

Розв’язання:

960 : 32 = 30 (в.) – продуктивність праці за 1 хв першого насоса;
960 : 48 = 20 (в.) – продуктивність праці за 1 хв другого насоса;
1000 : (30 + 20) = 20 (хв) – час викачування насосами 1000 відер води.

Відповідь: за 20 хв насоси разом викачають 1000 відер води .

Автомобілем ГАЗ можна перевезти 600 центнерів вугілля за 24 рейси, а автомобілем КамАЗ – за 12 рейсів. За скільки рейсів можуть перевезти все вугілля обидві машини?

600 : 24 = 25 (ц) – вантажопідйомність ГАЗа;
600 : 12 = 50 (ц) – вантажопідйомність КамАЗа;
600 : (25 + 50) = 8 (р.) – здійснять обидві вантажівки.

Відповідь: 600 ц вугілля обидві вантажівки перевезуть за 8 рейсів.

Через, одну трубу басейн наповнюється водою за 4 год, а через другу — за 6 год. Яку частину басейну наповнять водою дві труби, працюючи разом, за 1 год?

Розв'язання:

Об'єм басейна приймаємо за 1. Перша труба за 1 год заповнює частину басейну. Друга труба за 1 год заповнює частину басейну. Яку частину басейну наповнять водою за 1 год дві труби? Тому:

Відповідь: басейну.

Один тракторист може зорати поле за 12 год, а другий — за 24 год. За скільки годин два трактористи можуть зорати поле разом?

Розв’язання:

Час виконання роботи, год

Продуктивність

за 1 год

І тракторист

ІІ тракторист

частини поля зорють трактористи за 1 год , працюючи разом. Тому час виконання роботи 8 год.

Відповідь: за 8 год трактористи зорють поле.

У зв'язку з підвищенням продуктивності праці час, який потрібний для виконання певної роботи, зменшився на 28 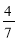%. На скільки відсотків підвищилась продуктивність праці?

Розв'язання:

Якщо прийняти час до його зменшення 100%, то після зменшення він становитиме:

*Час виконання роботи, %*	*Продуктивність праці, %*
100	100
100 - 28=71	х
Величини обернено пропорційні

Складемо пропорцію:

х : 100 = 100 : 71;

х = =140;

140 – 100 = 40%

Отже, продуктивність праці збільшилась на 40%.

Бригада виконує деяку роботу за 5,6 год. За який час виконує бригада ту саму роботу, якщо продуктивність праці зростає в 1,4 рази?

Розв’язання

*Час виконання роботи, год*	*Продуктивність праці*
5,6	1
х	1,4
Величини обернено пропорційні

Складемо пропорцію:

; (год)

Відповідь: бригада виконає роботу за 4 год.

Два ковалі, працюючи разом, можуть виконати певну роботу за 8 днів. За скільки другий коваль може виконати цю роботу сам, якщо перший коваль виконує її за 12 днів?

Розв’язання:

	*Час виконання роботи, дні*	*Частина роботи за 1 день*
І коваль	12
ІІ коваль	х
Разом	8

Розв’язуємо рівняння:

; ; ; х = 24 дні

Відповідь: другий коваль виконає роботу за 24 дні.

Один фонтан наповнює басейн за 2 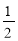год, а другий за 3год. За який час наповнять басейн обидва фонтани разом?

Розв’язання:

Позначивши об’єм басейна числом 1, маємо:

	*Час наповнення басейну, год*	*Частина роботи за 1 год*
І фонтан
ІІ фонтан
Разом	х

Час наповнення басейна обома фонтанами: год

Відповідь: фонтани наповнять басейн за 1,5 год.

Бак вміщує 15 відер води. Через скільки годин може наповнитися цей бак, якщо кран і зливний отвір відкриті. Через кран щогодини вливається 10 відер води, а через зливний отвір щогодини виливається 7 відер води.

Розв’язання:

Складемо таблицю:

	*К-сть відер води*	*Час для наповнення басейну, год*
Вливається	10	15 : 3 = 5
Виливається	7
Порівняння	10 – 7 =3

Відповідь: через 5 год басейн наповниться водою.

ВИКОРИСТАНІ ДЖЕРЕЛА:

Ігрові технології на уроках як складова виховання творчої особистості. [Електронний ресурс]. – Режим доступу: http://wiki.ciit.zp.ua
Маркова І. С. Урок математики в сучасних технологіях: теорія і практика. – Х.: Основа, 2007. – 176 с.
Мусіна О.І. Задачі на побудову. // Математика. – 2008. – №16.
Практичні роботи по геометрії у 5 класі. [Електронний ресурс]. – Режим доступу: http://www.uchportal.ru
Сахарук М.М. Задачі прикладного змісту. [Електронний ресурс]. – Режим доступу: http://school-2.at.ua
Сидорова О.П. Використання задач прикладного змісту. [Електронний ресурс]. – Режим доступу: http://ternivka-mo.edukit.dp.ua
Цикл уроків з теми «Випадкова подія. Імовірність випадкової події». [Електронний ресурс]. – Режим доступу: http://ternivka-mo.edukit.dp.ua

doc

Завантажити

Зберегти на потім

Додав(-ла)

Саламаха Руслана Ярославівна

Пов’язані теми

Математика, 5 клас, Матеріали для друку

Додано

11 березня 2023

Переглядів

1354

Оцінка розробки

Відгуки відсутні