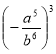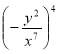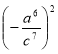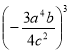Цикл уроків з алгебри 7 клас. Тема «Степінь».

Урок № 22

Тема.  Властивості степеня  з   натуральним  показником.

Мета: Формування навичок застосування  властивостей  степеня  з 

            натуральним  показником  при  спрощенні  виразів  і  розв’язуванні 

            рівнянь; користуватися  властивостями  степеня  при  визначенні 

            значень  числових  виразів  та  при  порівнянні  чисел. Розвивати

            увагу, логічне мислення, обчислювальні навики. Прививати навики

           самостійної праці, виховувати культуру спілкування.

Тип уроку: урок   застосування  знань,  формування  умінь та навичок  учнів.

Хід уроку

I. Організаційний момент. Перевірка домашнього завдання.

 (№ 303, 305, 310, 319)  Перевірка проводиться усно. Один учень зачитує відповіді, інші відмічають в зошиті правильні відповіді знаком «+», неправильні відповіді знаком « - »

II. Актуалізація опорних знань.  

Інтерактивна вправа «Робота в парах»

Вчитель задає питання. На перше питання відповідають учні першого варіанту, а учні другого варіанту оцінюють відповідь. На друге питання  - навпаки. Біля дошки працює один учень («експерт»), який після кожного питання озвучує правильну відповідь, таким чином, надає змогу провести всім учням  взаємоперевірку.

До кожного питання записати формулу.

1.               Сформулюйте  основну  властивість  степеня.
2.               Сформулюйте  правило  ділення  степенів  з  однаковими  основами.
3.               Як  піднести  степінь  до  степеня?
4.               За  яким  правилом  відбувається  піднесення  до степеня  добутку?
5.               Яким  чином  підноситься  до  степеня  частка?

6.        Яке число отримаємо при піднесення від’ємного числа до парної та

           степені?

7.        Яке число отримаємо при піднесення від’ємного числа до непарної   

           степені.

     «Експерт» на  дошці записує властивості  степеня  з  натуральним  показником:

III. Формування мети й задач уроку. Мотивація навчальної діяльності

• Я  хочу  розпочати  сьогоднішній  урок  із  питання,  яке,  здається,  недоречним  на  уроці  математики: „Як  ви  гадаєте,  чи  знають  дорослі  люди  та  діти  шкільного  віку  елементарні  правила  дорожнього  руху?” Ймовірна  відповідь: „Так!”

       -  А  чи  всі  користуються  ними,  тобто  чи  всі  застосовують  правила  дорожнього  руху  у  реальних  життєвих  ситуаціях?

Ймовірна  відповідь: „Ні!”

Нажаль,  таких  прикладів  можна  навести  чимало.  Ми  знаємо  правила,  чули  про  закони,  але  користуватися  ними  не  вміємо або  користуємося  невдало.  В  математиці,  як  у  житті!  Вивчив  правило – чудово,  а  чи  навчився  їм  користуватися?    Ми  з  вами  на  минулому  уроці познайомились і  довели властивості  степеня  з  натуральним  показником,  виходячи  з  цього,  як  ви  гадаєте,  чому  ми  маємо  присвятити  свій  сьогоднішній  урок?

Ймовірна  відповідь: „Тому,  щоб  навчитися  користуватися  вивченими  властивостями  степеня  на  практиці. ”

-  Дійсно,  на  сьогоднішньому  уроці  ми  маємо  навчитися  застосовувати  властивості  степеня  на  практиці. Для цього повторимо властивості  степеня  з  натуральним  показником; навчимося  застосовувати  властивості  степеня; розв’язувати  кілька  різноманітних  завдань,  в  яких  треба  застосувати  властивості  степеня, перевірити  результати  своєї  навчальної  діяльності  під  час  виконання  самостійної  роботи.

IV. Закріплення знань, умінь, навичок.

1. «Алгебраїчна ромашка»

На дошці намальована «алгебраїчна ромашка». Користуючись властивостями степеня з натуральним показником, на пелюстках  ціє  «ромашки»  написати  приклади,  які  б  дорівнювали  виразу  в   середині. 

 

Учні  пропанують  свої  варіанти  прикладів,  учитель  вписує  їх  у  пелюстки  „алгебраїчної  ромашки ”,  корегує  приклади  і  правильність    математичного  мовлення  учнів,  якщо  це  потрібно.

2. Тренувальні  вправи.

Завдання  уроку
під  керівництвом  учителя	самостійно із  перевіркою  в  класі	за  бажанням ( додаткове )
1.  Запишіть  у  вигляді  степеня:
а)  (а2)3 ∙ (a3a4)2; б)  (х3)4 ∙ (х2х5)6;	в)  (y3y5)4 ∙ (y2)6	г)  (2x3xk)2 ∙ (x3k)2
2.  Спростіть  вираз:
а)  (-53)7 ∙ (-52)4; б)  (-94)2∙ (-95)3;	в)  (-43)5 ∙ (-42)3	г)  (-х2х5)4 ∙ (-3х)3
3.  Знайдіть  значення  виразу:
а)  ;        б)  ;	в)	г)
4. Відпочинок  (змагання)
5.  Піднесіть  до  степеня  дріб:
а)  ;     б)  ;	в)	г)
6.  Порівняйте:
а)  85  та  214; б)  1253  та  255	в)  93  та  272	г)  та  (2,75)8
7.  Розв’яжіть  рівняння:
а)  (х2х)4 = 1; б)  (у5у3)2 = -1.	в)  (х4х3)5 – 1 =0.	г)  х6 = 212

 Завдання  4 – «Відпочинок».   Найкращій  відпочинок – це  зміна  праці.  Отже,  пропаную  змінити  форму  нашої  роботи  і  провести  невеличке  змагання.  Клас   об’єднується  у  три  команди: І  ряд – І  команда,  ІІ  ряд – ІІ  команда,  ІІІ  ряд – ІІІ команда.  Кожна  команда  отримає  своє  завдання,  яке  складається  з  чотирьох  прикладів.  Учні  кожної  парти  працюють  разом,  знаходять  вірне  рішення  свого  приклада  і  передають  листочок  із  завданнями  далі.  Зрозуміло,  що  переможе  команда,  яка  швидше  за  інші  і  абсолютно  вірно  виконає  завдання. 

Завдання для змагань

І  команда 1)  а11  ∙  *  = а16; 2)   *  :  а6  = а3; 3)  ( * )2  =  а14; 4)  а3  ∙  *  = а9.

ІІ  команда 1)  х3  ∙  *  = х15; 2)   *  :  х7  = х2; 3)  ( * )3  =  х12; 4)   х3 ∙  *  = х10.

ІІІ  команда 1)   *  ∙  у2  = у7; 2)  у14  :  *  = у11; 3)  ( * )3  =  у9; 4)  у3  ∙ *  = у8 .

Відповіді завдань

І  команда 1)  а5; 2)  а9; 3)  а7; 4)  а6.

ІІ  команда 1)  х12; 2)  х9; 3)  х4; 4)  х7.

ІІІ  команда 1)  у5; 2)  у3; 3)  у3; 4)  у5.

Підводяться підсумки змагань.

V. Самостійна робота із самоперевіркою.  ( 2 хв.) 

САМОСТІЙНА  РОБОТА

Варіант  1        ________________________________________

                                                            ^{ПІ  учня}

1. Знайдіть,  які  з  даних  рівностей  неправильні:                                   ( 1 бал)

А) х⁵ ∙ х³ = х⁸;     Б) а¹² : а³ = а⁴;     В) х⁶у⁶ = (ху)¹²;     Г) (а³)² ∙ а⁴ = а¹⁰.

2. Подайте  вираз  у  вигляді  степеня  з  основою  а.                      ( 1 бал)

А) а⁸;                   Б) а³;                    В) а²;                       Г) а⁴.

3. Виконайте  піднесення  до  степеня:  (- 3х³)³.                                       (2 бали)

А) -9х⁹;                Б) -9х⁶;                В) -27х⁹;                 Г) 27х⁹.

4. Чому дорівнює  значення  виразу  4³ : 2⁶  ?                                           (2 бали)

А) 1;                     Б) 2;                    В) 32;                      Г) 4.

5. Які  з  нерівностей  правильні ?                                                             (2 бали)

А) 2⁵ < 2⁶;                    Б) 2⁰ < 2;                    В) < ;              Г) 2¹ > 2.

6. Розв’яжіть  рівняння   х²х⁴ = 1.                                                               (2 бали)

А) 1;                     Б) 1;                 В) -1;                      Г) немає  розв’язків.

Кількість  балів:   _______

 

Варіант  2       __________________________________________

                                                             ^{ПІ  учня}

1. Знайдіть,  які  з  даних  рівностей  неправильні:                                  ( 1 бал)

А) х⁶ ∙ х⁴ = х²⁴;     Б) а¹⁵ : а³ = а⁵;     В) х⁴у⁴ = (ху)⁴;      Г) (а⁷)² ∙ а⁴ = а¹⁸.

2. Подайте  вираз  у  вигляді  степеня  з  основою  а.                      ( 1 бал)

А) а⁸;                   Б) а³;                     В) а²;                       Г) а⁴.

3. Виконайте  піднесення  до  степеня:  (- 2х³)⁴.                                       (2 бали)

А) 8х¹²;                Б) 8х⁷;                  В) -16х¹²;                Г) 16х¹².

4. Чому дорівнює  значення  виразу  9³ : 3⁶  ?                                           (2 бали)

А) 0;                     Б) 3;                     В) 9;                         Г) 1.

5.  Які  з  нерівностей  правильні ?                                                            (2 бали)

А) < ;     Б) 3⁵ < 3⁷;            В) 3⁰ < 2;                 Г) 3¹ > 3.

6. Розв’яжіть  рівняння   х²х⁴ = -1 .                                                            (2 бали)

А) 1;                     Б) 1;                  В) -1;                       Г) немає  розв’язків.

Кількість  балів:   ______

ВІДПОВІДІ  ТЕСТІВ  (на  зворотному  боці  дошки)

Варіант  1                    Варіант  2

1. Б, В;                         1. А, Б;

2. Г;                              2. В;

3. В;                              3. Г;

4. А;                              4. Г;

5. А, Б;                          5. Б, В;

6. Б.                               6. Г.                             

Через  2  хв.  Виконується    самоперевірка  і  визначається  кількість   балів.

VI. Домашнє завдання.

Учні,  які  набрали  9,10  балів,  виконують  домашнє  завдання  ІІІ рівня.  Учні,  які  набрали  5 - 8  балів  мають  працювати  вдома  над  завданням  ІІ  рівня,    учні,  які  набрали  1 - 4  бали,  перш  за  все  повинні  вдома повторити  властивості  степеня  і  відповідні  формули.  Після  цього  ви  маєте  виконувати  домашнє  завдання  І  рівня.

  І рівень: №  320 (а – д)                ІІ рівень: № 325                 ІІІ рівень: №  321                     

Творче завдання: приготувати свої «алгебраїчні ромашки». З  них  ми складемо чарівний  букет  і  використаємо  його  при  оформленні  математичної  газети  на  тижні  математики.

VII.  Підведення  підсумків  уроку.

Учитель  озвучує  і  коментує  оцінки  учнів,  які  активно  працювали  протягом  уроку. Учні,  які  виконували  додаткові  завдання,  мають  здати  зошити  для перевірки   результатів.  

VIII. Рефлексія

 Пропаную  повернутися  до  проблеми,  яку  ми  підняли  на  початку  уроку: Чи  досить  у  навчанні,  у  роботі,  у  житті  лише  знати  певні  правила,  закони  чи  властивості?  До  яких  висновків  ви  дійшли?

Ймовірна  відповідь:

- Ні,  недостатньо  вивчити  правила  чи  формули,  треба  навчитися  ними  користуватися,  тобто  застосовувати  на  практиці.

Цикл уроків з алгебри 7 клас.

Тема «Степінь»

№ уроку	Зміст уроку	Дата	Примітка
Тема 3.     (10 годин) Степінь з натуральним показником. Одночлен.
19	Степінь з натуральним показником		комбінований
20	Степінь з натуральним показником		закріплення знань
21	Властивості степеня з натуральним показником		засвоєння нових знань
22	Властивості степеня з натуральним показником		застосування знань
23	Властивості степеня з натуральним показником		узагальнення знань

Уроки  №№ 19 - 23

Урок № 19

Тема. Степінь з натуральним показником

Мета: повторити, систематизувати й узагальнити знання учнів про означення степеня з натуральним показником та вдосконалити вміння обчислювати значення виразів, що містять степені з натуральним показ­ником поряд з іншими арифметичними діями; розвивати навички самоконтролю, логічне мислення, пам'ять, увагу; відпрацювати вміння чита­ти та записувати степені; виховувати культуру писемного та усного мовлення, культуру спілкування.

Тип уроку: комбінований

Хід уроку

I. Організаційний момент

II. Актуалізація опорних знань. Вправа «Мікрофон»

1. Як знайти добуток десяткових дробів? Наведіть приклади.
2. Обчисліть:

     а) 0,7 · 0,7;       б) 0,2·  0,2 · 0,2;         в) 0,1 ·  0,1 · 0,1 · 0,1 · 0,1 · 0,1 .

3. Як знайти добуток звичайних дробів? Наведіть приклади.
4. Обчисліть:

     а)  ·  ;         б) ) · · ;            в) · · · .

5.  Яке число називають від’ємним? Наведіть приклади.
6. Яке число називають парним? Наведіть приклади.
7.  Як знайти добуток від’ємних чисел? Від чого залежить знак добутку декількох від’ємних чисел? Наведіть приклади.
8.  Обчисліть:

      а) −6 · (−6);       б) −3 · (−3) · (−3) ;           в) −2· (−2) · (−2) · (−2).

III. Повідомлення теми та задач уроку. Мотивація навчальної діяльності учнів.

Неважко виконати обчислення: 2 · 2 = 4. Та й записати нескладно. А якщо треба обчислити добуток дев’яти множників, кожний з яких дорівнює 2? Ви знаєте,  що вираз a + a + a + a + a + a можна записати коротше. А саме, суму декількох однакових доданків можна замінити добутком, тобто a + a + a + a + a + a = a· 6. А чи можливо добуток кількох однакових множників записати коротше? Наприклад,вираз a · a · a · a · a · a? Це можна зробити за допомогою степеня. Сьогодні ми вивчимо означення степеня. Звичайно, що зручно записувати добуток, у якому всі множники рівні, коротко — так ми маємо п’яту арифметичну дію — піднесення числа до степеня.

IV. Узагальнення та систематизація знань

 

                                 

 

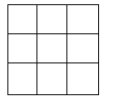
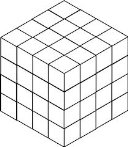
Розгляньте малюнок. Квадрат зі стороною 3 одиниці складається з 3 · 3 = 9 одиничних квадратів. Куб зі стороною 4 одиниці містить 4 · 4 · 4 = 64 одиничних кубика. Ви знаєте, що добуток 3 · 3 позначають 3² (читають «3 в квадраті»); добуток 4 · 4 · 4 позначають 4³ (читають «4 в кубі»).

3 · 3 = 3²;     4 · 4 · 4 = 4³.

Так само позначають добуток будь якого числа однакових множників, наприклад:

3 · 3 · 3 · 3 · 3 · 3 = 3⁶;     · · · = ;     (-4) · (-4) · (-4) · (-4) · (-4)  = (-4)⁵;

6 = 6¹; 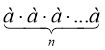                  = а ⁿ

(читають «степінь числа а с показником n», -  коротко «а в степені n»).

Степенем числа а з натуральним показником n, більшим за 1, називають добуток n множників, кожний з яких дорівнює а.

Число  а називають основою степеня, а число n – показником степеня.

 

V.  Сприйняття  та усвідомлення нового матеріалу.

1. Степенем числа a з показником 1 називають саме число a. Наприклад,

7¹ = 7;     (-15)¹ = -15.

2. У разі піднесення до степеня додатного числа отримуємо додатне число.
3. У разі піднесення до степеня від’ємного числа можна отримати як додатне число, так і від’ємне. Степінь від’ємного числа з парним показником — додатне число, оскільки добуток парного числа від’ємних множників є додатним, а якщо показник непарний, то отримаємо від’ємне число, оскільки добуток непарного числа від’ємних множників є від’ємним.
4. Ви знаєте чотири арифметичні дії: додавання, віднімання, множення, ділення. Піднесення до степеня вважають п’ятою арифметичною дією. Піднесення до степеня — дія третього степеня і тому виконується в першу чергу. Якщо вираз без дужок містить дії різних степенів, то спочатку виконують дії вищого степеня, а потім нижчого.  Наприклад, під час обчислення виразу 2 · 5 ² - 32 спочатку треба піднести   до степеня, потім помножити, а потім відняти.

V. Засвоєння вмінь та навичок

 

Виконання усних вправ

1. Які з виразів є степенями? 5³; 5·3; 5³ + 3⁵;(-7)⁵; -7⁵; 5·7; (a + b)⁵; (a + b)·5.
2. Прочитайте степінь, назвіть основу й показник степеня: 6⁴; (2,1)⁹; 10².
3. Чи можна записати вираз у вигляді степеня? Якщо так, то назвіть осно­ву й показник: 4·4·4·4·4; (-2)·(-2)·(-2); 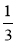··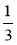·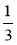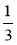; (ab)(ab)(ab).
4. Прочитайте вираз, використовуючи слова сума, різниця, добуток, квад­рат, куб:

5³; 6·5³; 8² + 3²;(8 + 3)²; 3·2³ + 5; а² + т²; (а + m)²; а³ – m³; (а – m)³.

Виконання письмових вправ

1. Знайдіть значення виразу:

Один учень  коментоване розв’язує  біля дошки :

1) 2⁵;  2) (-7)²;  3) (0,6)²;  4) 7²;  5); 6) ;7) ; 8) .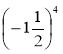

Потім № 257 учні виконують самостійно в зошиті. (2 учня працюють на дошці). Проводиться самоперевірка, корекція.

2. Обчисліть, попередньо прочитавши вираз:

1) 4³ + 3⁵;         2) (-8)² – (-1)¹⁰;          3) ;           4) (-0,6)³ – (-0,5)³.

3*. Запишіть числовий вираз та обчисліть його значення:

1) сума куба числа 5 і квадрата числа (-8);

2) куб різниці чисел 8 і 9;

3) різниця квадратів чисел -2 і 1.

VI. Підсумок уроку. Рефлексія

«Німий диктант» з наступною перевіркою

На дошці записано вираз:                3⁵

3 – ...                5 – ...                       3⁵...   243...

 VII. Домашнє завдання

Вчити §7.

Виконати №№:   *   258, 260;

                             ** 264; 267(а,б).

 

 

 

 

 

 

 

Урок № 21

Тема. Властивості степеня з натуральним показником

Мета:. домогтися свідомого розуміння учнями властивості добутку та частки  сте­пенів з однією основою, піднесення степеня до сте­пеня, степеня добутку й відношення. Сформувати вміння перетворювати числові та буквені вирази з використанням цієї властивості. Розвивати навики застосування властивості степеня при розв’язуванні практичних прикладів, виконанні раціональних обчислень. Виховувати культуру спілкування, культуру математичного мовлення; залучати учнів до активної діяльності в процесі самостійного пошуку.

Тип уроку: засвоєння нових знань.

Хід уроку

I. Організаційний момент

II. Актуалізація опорних знань. Вправа «Мозковий штурм»

- дати означення степеня з натуральним показником;

- пояснити, що являється основою степеня, показником степеня;

- яке число отримаємо при піднесення від’ємного числа до парної та непарної степені;

- чому дорівнює а¹; а⁰;

- назвати порядок дій в прикладах, які містять степінь;

- обчислити:

           1) 2³ · 3²;                2) 5 · 7²;           3) 10⁰ · 10³;            4) 5³ : 5²;

           5) 10⁴ : 10²;            6) (3²)⁴;            7) 5²· 5¹;                 8) 2³ · ()³.

Як можна раціонально розв’язати приклади 3, 4, 5, 6, 7, 8?

Серед учнів класу обов’язково знайдуться такі, що запропонують більш раціональне розв’язування цих прикладів, бо було задано випереджальне домашнє завдання на вивчення властивостей степеня.

III. Повідомлення теми та задач уроку. Мотивація навчальної діяльності

При обговорені раціонального розв’язування з’ясовується, що необхідно знати властивості  степеня з натуральним показником, і робиться висновок, що сьогодні на уроці буде вивчено властивості степеня з натуральним показником та розглянуто їх застосування при розв’язуванні різноманітних вправ.

IV. Усвідомлення нового матеріалу.   Технологія «Ажурна пилка»

На попередньому уроці було сформовано 4 групи - «червоні», «жовті», «зелені» та «сині»  по 5 учнів в кожній. Учням були роздані  кольорові картки  з номером на ній  (від 1 до 5). Групи отримали певні завдання:

 «червоні» - сформулювати, довести та пояснити на прикладах властивості степеня з натуральним показником «Множення степенів з однаковою основою»;

«сині» - сформулювати, довести та пояснити на прикладах властивості степеня з натуральним показником «Ділення степенів з однаковою основою»;

«жовті» - сформулювати, довести та пояснити на прикладах властивості степеня з натуральним показником «Піднесення степеня до степеня»;

«зелені» - сформулювати, довести та пояснити на прикладах властивості степеня з натуральним показником «Піднесення до степеня добутку і частки»

1. Учням пропонується об’єднатися в групи відповідно кольору картки, яку вони отримали («домашні» групи). Учні обмінюються інформацією, проводять взаємоопитування, розв’язують завдання, підготовлені вдома.

2. Учні об’єднуються в групи відповідно до своїх номерів («експертні групи»). В кожній «експертній» групі опиняються представники з кожної «домашньої» групи. Учасники формулюють, доводять, показують на прикладах застосування властивості степеня з натуральним показником, яку вивчали в «домашній» групі. У зошитах записують визначення, доведення та формули кожної з властивостей.

3. Учні об’єднуються в «домашні групи, учасники обмінюються між собою інформацією, отриманою в «експертних» групах.

V.  Первинне закріплення та корекція.

Учні займають свої місця. Пропонується розв’язати декілька вправ на застосування властивостей степеня з натуральним показником (коментоване розв’язування біля дошки).

с⁴ · (с³)⁴;              (с⁸)² : (с⁴)⁴;        ;       ;         ;        .  

VI. Підсумок уроку.

• які властивості степеня ви дізнались? Сформулюйте їх.
• Як ці властивості можна записати у вигляді формул?
• Чи сподобався вам спосіб, за допомогою якого ви вивчили ці властивості?

VII. Рефлексія

Учням пропонується на аркуші, який передається з парти на парту, поставити номер,  відповідний прізвищу учня в класному журналі ,в тій колонці, яка відображає розуміння нового матеріалу.

Нічого не розумію

Потрібна допомога

Все розумію

 

VII. Домашнє завдання

Вчити § 8

Виконати №№:   *     303, 305;

                             **   310, 319

 

 

 

 

 

 

 

 

 

Урок № 23

Тема. Властивості степеня з натуральним показником

Мета: узагальнити та систематизувати знання учнів про степінь з натуральним показником; закріпити та вдосконалити навики перетворення виразів, які містять степені; розвивати логічне мислення, свідомого сприйняття навчального матеріалу; виховувати культуру усного та писемного мовлення, культуру спілкування

Тип уроку: узагальнення та систематизація знань

Хід уроку

I. Організаційний момент

II. Перевірка домашнього завдання. «Знайди помилку».

№ 320 а) (ах)12 б) – (bу)7 в) (аbс)7 г) (-m)9 д) (2х)5

№ 325 а) х = -1 б) х = -1 в) х = 0 г) х = -1 д) х = 1

№ 321 а) 512 б) 610 в) 216 г) 0,15 д) (- 0,3)18

 

На дошці заготовлені відповіді до кожного номеру. В деяких з них допущені помилки. Кожен учень перевіряє завдання свого рівня. Йде обговорення  та виправлення помилок.

Зібрати «алгебраїчні» ромашки.

 ІІІ. Актуалізація опорних знань.

а). «Мікрофон». Учні відповідають на запитання  по черзі за правилами:

- говорити має право тільки той, у кого «символічний» мікрофон;

- коли хтось відповідає, інші не мають права перебивати, щось говорити;

- якщо відповідь була невірна, вчитель просить учня записати розв’язання прикладу на дошці, для подальшої корекції

Завдання: представити у вигляді степеня вираз (таблиця)

 

№ п/п	1	2	3	4	5
1	х5х8	у у12	у3 у2у	а4а3а2	с5с3сс6
2	(х3)2	(а5)4	(у2)5	(с5)2	(а5)5
3	а3х3	а7у7	х2у2z2	100х2у2	-8а3у3
4	х5(х2)3	(х3)4х	(х2)5х3	(аа6)3	(а2а3)2
5	(х3)3(х3)3	((х2)3)4	(х4)2(х5)3	(а3)2(а5)3	((а3)4)5

 

б). «Мозговой штурм»    

 

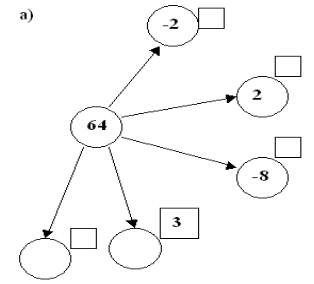
- Представити 64 в вигляді  степеня з основою 2; -2; -8.

- куб якого числа дорівнює 64?

- Чи існує ще який спосіб представлення  64 в вигляді  степеня з натуральным   

  показником? Якщо так, то назвіть його

IV. Комплексне застосування знань, умінь, навичок.

Коментоване розв’язування біля дошки

1). Обчислити:

2). Знайти значення виразу 125 – х⁴, при х = -2.

3). Знайти значення виразу 81 · ()⁴ – 0,05 · (-10)².

4). Обчислити: + х⁰; х ≠ 0

5). Розв’язування текстової задачі.  

Щоб пофарбувати куб витратили 40 грамів фарби. Чи вистачить   350 грамів фарби, щоб пофарбувати куб, ребро якого в три раза больше?

Відповідь: не вистачить.

V. Самостійна робота. (У кожного учня картка с завданням)                                             

Вариант 1 1). Виконати дії: а)                                 б) в)                        г)

2) Обчислити значення виразу:  а)                                б) в)                               г)

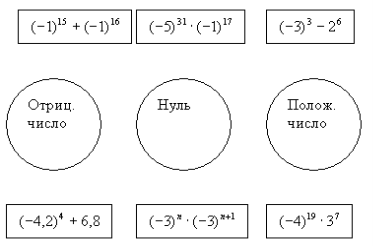
3) Показати за допомогою стрілки чи дорівнює значення виразу нулю, додатному числу, від’ємному числу:

 

Вариант 1 1). Виконати дії: а)                         б) в)                               г)

2) Обчислити значення виразу: а)б) в)     г)

3) Показати за допомогою стрілки чи дорівнює значення виразу нулю, додатному числу, від’ємному числу:

Картки з виконаним завданням здати на перевірку.

VI. Підсумки уроку.

Заповнити пропуски, щоб виконувалась рівність

1. (y²)² ∙ (…)³= y¹⁰.                  2. (…)² ∙ c³= c¹³.             3. b² ∙ (…)³= -27 b¹¹.

 VІI. Рефлексія. Оцінити степінь засвоєння матеріалу у відсотках, записати в зошиті.

VІІI. Домашнє завдання.

Виконати №№ :    *    311; 312

                               **   В.1 стор. 81