Дидактичні матеріали з алгебри для 7 класу "Лінійне рівняння з параметрами"
Лінійне рівняння з параметрами
Якщо в рівнянні ![]() буква х – змінна, а буква а – деяке число, то це рівняння з параметром а.
буква х – змінна, а буква а – деяке число, то це рівняння з параметром а.
Щоб розв’язати таке рівняння, потрібно розглянути такі випадки:
-
При
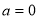 ,
, 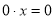 ;
;
-
При
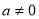 ,
, 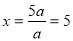 .
.
Відповідь: якщо ![]() , х – будь-яке число;
, х – будь-яке число;
якщо ![]() ,
, ![]() .
.
Лінійні рівняння з параметрами можна розв’язувати так само, як звичайні лінійні рівняння, тільки до тих пір, поки кожне перетворення можна виконати однозначно. Якщо ж якесь перетворення не можна виконати однозначно, то розв’язання потрібно розбити на декілька випадків і кожний випадок пояснити.
Схема дослідження лінійного рівняння
Схему розв’язків лінійного рівняння виду ![]() можна представити у вигляді сукупності трьох систем:
можна представити у вигляді сукупності трьох систем:
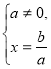 (1)
(1)
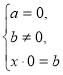
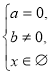 (2)
(2)
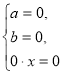
![]() (3)
(3)
Схему розв’язків лінійного параметричного рівняння ![]() можна представити у вигляді сукупності трьох систем:
можна представити у вигляді сукупності трьох систем:
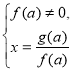 (1)
(1)
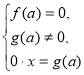
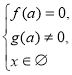 (2)
(2)
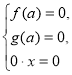
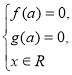 (3)
(3)
Приклади розв’язання лінійних рівнянь з параметрами.
Приклад 1.
Розв’язати рівняння ![]() .
.
Розв’язання.
![]() ,
,
![]() .
.
Якщо ![]() , то
, то ![]() ;
;
якщо ![]() , то
, то ![]() , х – будь-яке число.
, х – будь-яке число.
Відповідь: якщо ![]() ,
, ![]() ;
;
якщо ![]() , х – будь-яке число.
, х – будь-яке число.
Приклад 2.
Розв’язати рівняння ![]()
Розв’язання.
![]() ,
,
![]() .
.
Якщо ![]() , то
, то ![]() ;
;
Якщо ![]() , то
, то ![]() , х – будь-яке число.
, х – будь-яке число.
Відповідь: якщо ![]() ,
, ![]() ;
;
якщо ![]() , х – будь-яке число.
, х – будь-яке число.
Приклад 3.
Розв’язати рівняння ![]() .
.
Розв’язання.
![]() ,
,
![]() .
.
Якщо ![]() , то
, то ![]() .
.
Якщо ![]() , то
, то ![]() , рівняння розв’язків не має.
, рівняння розв’язків не має.
Відповідь: якщо ![]() ,
, ![]() ;
;
Якщо ![]() , розв’язків немає.
, розв’язків немає.
Приклад 4.
Розв’язати рівняння ![]() .
.
Розв’язання.
![]() ,
,
![]() .
.
Якщо ![]() , тобто
, тобто ![]() , то
, то ![]() .
.
Якщо ![]() , тобто
, тобто ![]() , то рівняння розв’язків не має.
, то рівняння розв’язків не має.
Відповідь: якщо![]() ,
, ![]() ;
;
Якщо ![]() , розв’язків немає.
, розв’язків немає.
Приклад 5.
Розв’язати рівняння ![]() .
.
Розв’язання.
![]() ,
,
![]() .
.
Якщо ![]() , то х – будь-яке число.
, то х – будь-яке число.
Якщо ![]() , то рівняння розв’язків немає.
, то рівняння розв’язків немає.
Відповідь: якщо ![]() , х – будь-яке число;
, х – будь-яке число;
якщо ![]() , рівняння розв’язків не має.
, рівняння розв’язків не має.
Приклад 6.
При якому значенні параметра а рівняння ![]() має безліч розв’язків?
має безліч розв’язків?
Розв’язання.
Застосовуючи схему дослідження лінійного параметричного рівняння, одержимо таку систему:
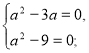
![]()
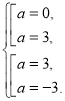
Звідси маємо ![]() .
.
Відповідь: якщо ![]() рівняння має безліч розв’язків.
рівняння має безліч розв’язків.
Приклад 7.
При якому значенні параметра а рівняння ![]() не має розв’язку?
не має розв’язку?
Розв’язання.
Рівняння не має розв’язку, якщо
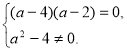
Звідки
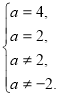
Відповідь: ![]() .
.
Приклад 8.
При яких значеннях параметра а рівняння ![]() має від’ємні розв’язки?
має від’ємні розв’язки?
Розв’язання.
Зведемо рівняння до загального вигляду. Отримаємо:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
За умовою ![]() , то
, то ![]() , звідки
, звідки ![]() .
.
Відповідь: ![]() .
.
Приклад 9.
Визначити, при яких значеннях параметра а корені рівняння ![]() кратні 5.
кратні 5.
Розв’язання.
Зведемо рівняння до загального виду. Отримаємо:
![]() ,
,
![]() ,
,
![]() .
.
Якщо ![]() , то рівняння має розв’язок:
, то рівняння має розв’язок: ![]() .
.
За умовою, корені рівняння кратні 5, тобто
![]() , де
, де ![]() ,
, ![]() .
.
Звідси ![]() ,
, ![]() , де
, де ![]() ,
, ![]() .
.
Відповідь: ![]() , де
, де ![]() ,
, ![]() ,
, ![]()
Приклад 10.
Розв’язати рівняння: ![]() .
.
Розв’язання.
![]() ,
,
![]() ,
,
![]() .
.
Якщо ![]() , b – будь-яке число, то
, b – будь-яке число, то ![]() .
.
Якщо ![]() , b – будь-яке число, то рівняння має безліч розв’язків.
, b – будь-яке число, то рівняння має безліч розв’язків.
Відповідь: якщо ![]() ,
, ![]() , то
, то ![]() ;
;
якщо ![]() ,
, ![]() , то рівняння має безліч розв’язків.
, то рівняння має безліч розв’язків.
Приклад 11.
Розв’язати рівняння:
![]() .
.
Розв’язання.
При ![]() і
і ![]() дане рівняння не існує, а тому розв’язків також немає. Всі інші значення а утворюють область допустимих значень параметра а:
дане рівняння не існує, а тому розв’язків також немає. Всі інші значення а утворюють область допустимих значень параметра а: ![]() .
.
Після певних перетворень маємо:
![]()
![]()
![]()
![]()
![]()
Якщо ![]() , тобто
, тобто ![]() і
і ![]() , то
, то ![]() .
.
Якщо ![]() , то
, то ![]() ,
, ![]() . Рівняння розв’язків немає.
. Рівняння розв’язків немає.
Якщо ![]() , то рівняння матиме вигляд
, то рівняння матиме вигляд ![]() , а таке рівняння має безліч розв’язків.
, а таке рівняння має безліч розв’язків.
Відповідь: якщо ![]() , то
, то ![]() ;
;
якщо ![]() , то розв’язків немає;
, то розв’язків немає;
якщо ![]() , то
, то ![]() .
.
Приклад 12.
Розв’язати рівняння:
![]() .
.
Розв’язання.
ОДЗ: ![]() .
.
Маємо:
![]() ,
,
![]() ,
,
![]()
![]()
![]()
Якщо ![]() , тобто
, тобто ![]() , то
, то ![]() .
.
Якщо ![]() , тобто
, тобто ![]() , то
, то ![]() і рівняння не має розв’язків.
і рівняння не має розв’язків.
Оскільки ![]() , то знайдемо ті а, при яких рівняння матиме корінь
, то знайдемо ті а, при яких рівняння матиме корінь ![]() . Ці значення а треба виключити.
. Ці значення а треба виключити.
![]() ,
,
![]()
![]()
![]()
![]() .
.
Відповідь: якщо ![]() , то
, то ![]() ;
;
якщо ![]() , то розв’язків немає.
, то розв’язків немає.
Приклад 13.
При яких значення параметра а число ![]() є коренем рівняння
є коренем рівняння ![]() .
.
Розв’язання.
![]()
![]()
![]()
Підставимо у рівняння замість х число ![]() і розв’яжемо його відносно а.
і розв’яжемо його відносно а.
![]()
![]()
![]()
![]()
![]() .
.
Відповідь: ![]() .
.
Приклад 14.
Дано рівняння ![]() .
.
-
Розв’язати рівняння при
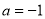 .
.
-
Знайти значення параметра а, при яких число
 є коренем рівняння.
є коренем рівняння.
- Розв’язати рівняння відносно х.
- При яких значеннях а рівняння має невід’ємний корінь?
Розв’язання.
1. Якщо ![]() , то рівняння набуде вигляду:
, то рівняння набуде вигляду:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
2. Число ![]() буде коренем рівняння, якщо при підстановці його в рівняння отримаємо правильну рівність. Отже, маємо:
буде коренем рівняння, якщо при підстановці його в рівняння отримаємо правильну рівність. Отже, маємо:
![]()
ОДЗ: ![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
; ![]() .
.
3. ![]() ,
,
![]() ,
, ![]()
![]() ,
,
![]() ,
,
![]() .
.
Якщо ![]() і
і ![]() , то
, то ![]() ;
;
якщо ![]() або
або ![]() , то рівняння розв’язків не має;
, то рівняння розв’язків не має;
якщо ![]() , то рівняння має безліч розв’язків.
, то рівняння має безліч розв’язків.
4. Корінь рівняння ![]() є невід’ємним, якщо
є невід’ємним, якщо ![]() .
.
![]() .
.
Слід врахувати, що при ![]() ,
, ![]() рівняння не має розв’язків, а при
рівняння не має розв’язків, а при ![]() - безліч розв’язків. Ці числа виключаємо із числового проміжку.
- безліч розв’язків. Ці числа виключаємо із числового проміжку.
Отже, ![]() .
.
Відповідь:
1. ![]() ;
;
2. ![]() ;
; ![]() ;
;
3. якщо ![]() , то
, то ![]() ;
;
якщо ![]() , то рівняння розв’язків не має;
, то рівняння розв’язків не має;
якщо ![]() , то рівняння має безліч розв’язків;
, то рівняння має безліч розв’язків;
4. ![]() .
.
Тренувальні вправи.
Розв’язати рівняння
1. ![]() ,
,
2. ![]() ,
,
3. ![]() ,
,
4. ![]() ,
,
5. ![]() ,
,
6. ![]() ,
,
7. ![]() .
.
8. При якому значенні параметра а рівняння ![]() не має розв’язку?
не має розв’язку?
9. При якому значенні параметра а рівняння ![]() має безліч розв’язків?
має безліч розв’язків?
10. Визначити, при яких значеннях параметра а рівняння ![]() має додатні розв’язки?
має додатні розв’язки?
11. При яких значеннях параметра а число ![]() є коренем рівняння
є коренем рівняння ![]() .
.
12. Знайти всі дійсні значення параметра а, при яких рівняння ![]() має корінь, що задовольняє умові
має корінь, що задовольняє умові ![]() .
.
13. При яких значення параметра а рівняння ![]() має від’ємний корінь?
має від’ємний корінь?
-
Дякую.


про публікацію авторської розробки
Додати розробку
