Урок на тему "Одночлен. Піднесення одночленів до степеня. Множення одночленів"

Тема уроку: Розвязування вправ із теми «Одночлен. Піднесення одночленів до

                      степеня. Множення одночленів»

Мета уроку:

• узагальнити та систематизувати знання та вміння учнів, набуті в ході вивчення названої теми;
• сприяти розвитку колективної праці, активізуючи дію між учнями, спонукати до пізнавальної діяльності;
• виховувати працьовитість, активність, дисциплінованість та кмітливість.

Тип уроку: узагальнення знань.

Хід уроку:

І. Організаційний момент.

Привітання, перевірка присутніх, готовність учнів та дошки до роботи, організаційні питання.

Сьогодні на уроці

знову світ степеня нас чекає

і порозуміння з ним вам я бажаю.

Хай очі ваші світяться яскраво,

і на уроці вам буде цікаво.

ІІ. Перевірка домашнього завдання.

ІІІ. Актуалізація опорних знань

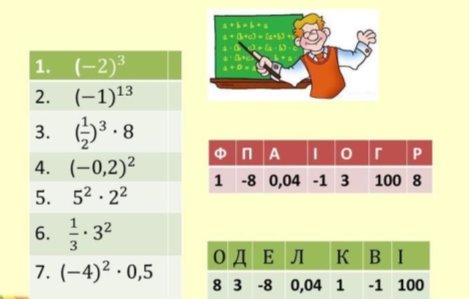
А зараз згадаємо видатних математиків, які займалися цією наукою ще до нашої ери.

Давайте з вами пригадаємо основні властивості степеня, що потрібно буде для подальшої нашої роботи: 

Властивості степеня

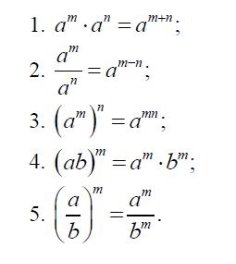
ІV. Узагальнення та систематизація вмінь і навичок

 Для повторення раніше вивченого матеріалу, поділимося зараз на 3 групи. При виконанні завдань (за потребою) дозволяється користуватися підручником.

Завдання для 1 ряду: дати відповідь на питання: що називають степенем одночлена? Навести приклад.

Завдання для 2 ряду: сформулювати правило множення двох або кількох одночленів та навести приклад.

Завдання для 3 ряду: сформулювати правило піднесення одночлена до степеня та навести приклад.

V. Застосування вмінь

 Робота з підручником (№ 276, 278, 280)

VІ. Перевірка знань (робота в парах)

Математичний диктант

1. У одночлені 3⁵ число 3 є степенем. (-) основою
2. Вирази (a⁴)⁷ та a²⁸ є тотожними. (+)
3. Вираз (-3)⁷ · (-5)¹⁰ набуває додатних значень. (-)
4. Вираз 2a¹⁰ + 5b є одночленом. (-)
5. Коефіцієнт одночлена 3,5ху³ · 2у⁶ є число 7. (+)
6. Одночлен 4ху³ · 2у⁶ записано в стандартному вигляді. (-)
7. Степінь одночлена 4ху³2с⁶ дорівнює 10. (+)
8. Виконати піднесення до степеня (3а²b)². (9а⁴b²)
9. Спростити вираз 12а² · 5а³ b⁷. (60а⁵b⁷)
10. Виконайте множення одночленів . ()
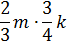11. Знайдіть розвязок рівняння х⁵ = -1. (-1)

(Учні перевіряють завдання, працюючи в парах)

VІІ. Підсумки уроку

Кросворд

Завдання для «допитливих»

VІІІ. Оцінювання учнів

ІХ. Домашнє завдання

 Повторити п.7 (стор. 47-49), виконати № 277, 279.