Електричний струм в металах
Чупахіна О.В.
Електричний струм в різних
середовищах
метали
2020
З М І С Т
1.1. Класична електронна теорія провідності металів
Вивчаючи електричний струм ми, як усім відомий факт, використовуємо знання про те, що метал є гарним провідником електричного заряду. Обґрунтовуючи це згадуємо про особливість внутрішньої будови металів, про виняткову металічну кристалічну гратку. В цьому розділі спробуємо детальніше розібратися з особливостями металів, які дозволяють нам їх використовувати у якості провідників.
На початку ХХ століття німецьким вченим Паулем Друде (1863-1906) та майбутнім Нобелівським лауреатом Хендріком Лоренцом (1853-1928) створено класичну теорію провідності металів. Згідно якої метали складаються з позитивних іонів, що коливаються навколо певного положення рівноваги, та вільних негативних електронів, що утворилися при відриванні від атомів. Ці електрони можуть вільно пересуватися по всьому об’єму металу, того власне і отримали назву «вільних». За відсутності електричного поля , електрони хаотично рухаються, зіштовхуючись з іонами кристалічної гратки. Сукупність цих електронів можна наближено розглядати, як деякий електронний газ, що описується законами ідеального газу і підлягає законам класичної механіки. Середня швидкість теплового руху електронів, за кімнатної температури, складає приблизно 105 м/с.
1.2. Дослід Рікке
Електронна теорія провідності металів підкріплюється й дослідами, що з’являються майже одночасно зі створенням теорії. Серед таких дослідів варто виділити дослід Рікке, проведений в 1901 році німецьким фізиком-експериментатором Едуардом Рікке (1845— 1915).
Оскільки будова металів передбачає наявність двох типів заряджених частинок – електронів та позитивних іонів. То носіями струму в металах ймовірно можуть бути обидва типи частинок. Для з’ясування справжніх носіїв заряду Рікке вирішує використати три відполірованих циліндри однакових розмірів. Два циліндри виготовлені з міді, а третій – з алюмінію.
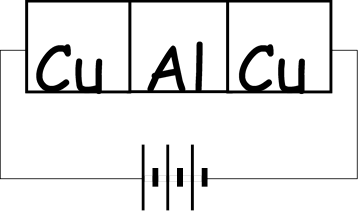Під’єднавши до джерела напруги ці циліндри так, як показано на малюнку, Рікке пропускає колом струм величиною 0,1 А протягом року. За цей час через кожен циліндр проходить заряд в 3,5 мільіони Кулонів. Вчений очікує, що якщо при детальному дослідженні циліндрів
після річного пропускання струму, в мідному будуть виявлені іони алюмінію, а в алюмінієвому – іони міді, то це стане доказом того, що носіями заряду в металах є іони. Якщо ж метали не змішаються – то носіями є заряджені частинки, однакові для всіх металів – електрони. Звичайно, що метали виявились майже чистими (виявлено лише незначні домішки спричинені дифузією),що підтвердило теорію електронної провідності металів.
1.3. Дослід Папалексі – Мальденштама.
(дослід Стюарта - Толмена)
T
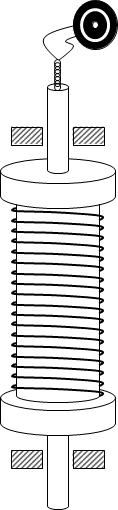
В 1913 році російські вчені М.Д. Папалексі (1880 - 1947) та О.Е. Мальденштам (1891-1938) спробували експерементально підтвердити існування вільних носіїв струму в металах. Оскільки носії є частинками, що мають масу, то вони мають підкорюватись законам механіки, зокрема закону інерції. Наприклад, якщо рухомий провідник різко загальмувати, то частинки ще деякий час продовжуватимуть рухатись в тому ж напрямі за інерцією, так само як пасажири в автобусі, що виконує аварійне гальмування.
Для цієї перевірки дослідники використали обертальні коливання котушки з дротом під’єднаним до динаміка вугільного телефону. При різкому гальмуванні котушки телефон видавав клацання, що свідчило про рух за інерцією вільних носіїв заряду.
В 1916 році американські вчені Річард Толмен (1881 - 1941) та
Томас Стюарт (1890 - 1958) вдосконалюють дослід Папалексі та
Мальденштама. Замінивши телефон на надчутливий для тих часів гальванометр, американці змогли визначити масу носія заряду в металі. Знайдене ними значення приблизно рівне сучасному значенню маси електрона 9,1∙10-31 кг.
1.3. Швидкість руху електронів. Швидкість поширення струму.
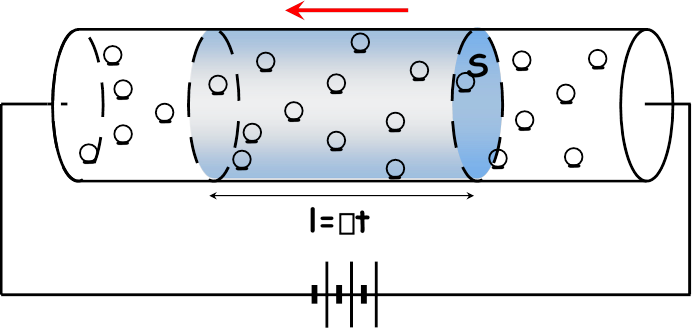
Знайдемо середню швидкість з якою рухаються електрони в металевому провіднику перерізом S, якщо по ньому тече струм величиною І, а концентрація електронів провідності n.
I
За означенням сили струму
Оскільки носіями заряду є електрони, то:
,
де е – величина заряду електрона ( е = 1,06∙10-19Кл ) ,а N – кількість електронів, що
пройдуть через обраний переріз провідника за час t.
Якщо вважати, що всі електрони рухаються з однаковою швидкістю , то через
обраний переріз площею S, за час t пройдуть лише ті електрони які віддалені від перерізу не більше ніж на відстань l=t,
тобто усі електрони, що знаходяться у об’ємі циліндру з площею поперечного перерізу S та висотою l=t.
V = l∙S = tS
За визначенням концентрація це величина, що характеризує кількість частинок в одиниці об’єму:
Звідки N = nV, отже
N =n∙tS
Тоді загальний заряд, що пройшов через обраний переріз:
,
а сила струму, що тече провідником:
Отже:
Оцінимо середню швидкість руху електронів в мідному провіднику перерізом 1мм2, якщо по ньому тече струм величиною в 1 А. Концентрація вільних електронів в міді складає 8,5∙1028 м-3.
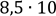
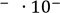
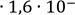Кл
Таким чином, швидкість впорядкованого руху електронів становить лише долі сантиметра за секунду.
Якщо ж звернутися до електронної теорії провідності металів, та розглянути електрони як частинки електронного газу, то за кімнатної температури вони рухаються зі швидкістю 
.Отже, швидкість хаотичного руху електронів у мільярд разів
більша за швидкість впорядкованого руху. Це означає, що строго впорядкований рух електронів уздовж провідника не можна вважати електричним струмом. Під дією електричного поля електрони, рухаючись хаотично, поступово зміщуються по провіднику (здійснюється дрейфовий рух електронів) на кілька міліметрів за секунду. Але як тільки в провіднику виникає електричне поле, воно з величезною швидкістю, близькою до швидкості світла у вакуумі (300 000 км/с), поширюється по всій довжині провідника. Одночасно з поширенням електричного поля всі електрони починають рухатися в одному напрямку по всій довжині провідника. Так, наприклад, при замиканні ланцюга електричної лампи в впорядкований рух приходять і електрони, наявні в спіралі лампи.
1.4. Залежність опору металів від температури
Оскільки середня швидкість теплового руху електронів провідності і енергія коливань іонів у вузлах кристалічних ґраток збільшуються зі збільшенням температури металевого провідника, то зростає і частота зіткнень електронів з іонами, а отже зростає опір провідника.
Якщо при температурі 0ºC опір провідника дорівнює R0, а при температурі t він дорівнює R, то відносна зміна опору, як показує дослід, прямо пропорційна зміні температури t:
Коефіцієнт пропорційності називають температурним коефіцієнтом опору. Він характеризує залежність опору речовини від температури. Температурний коефіцієнт опору чисельно дорівнює відносній зміні опору провідника під час нагрівання на 1 оС. Для більшості металів його значення можна відшукати в спеціальних таблицях.
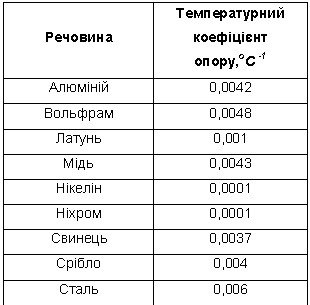
При аналізі наведеної таблиці помітно що чисті метали мають дуже близькі за значенням температурні коефіцієнти опору. Це значення приблизно рівне:
Від нагрівання геометричні розміри провідника мало змінюються. Його опір змінюється переважно внаслідок зміни питомого опору:
Оскільки майже не залежить від температури, то
питомий опір лінійно залежить від температури
ρ=ρ0(1+t)
Сплави з високим питомим опором (наприклад, для
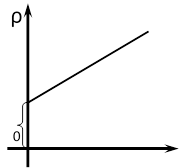сплаву міді з нікелем - константану ρ ≈10-6 Ом·м) ρ
використовують для виготовлення еталонних опорів, 0 t тобто у тих випадках, коли потрібно, щоб опір помітно не змінювався зі зміною температури.
Залежність опору металів від температури використовують у термометрах опору.
У 1911 р. голландський фізик Камерлінг-Оннес, вивчаючи температурну залежність питомого опору ртуті в області низьких температур, знайшов дивовижне явище: при температурі Т = 4,2 К опір ртуті практично стрибком зменшувався до нуля. Ртуть переставала чинити опір проходженню електричного струму. Це явище одержало назву надпр відн ті. В наш час воно встановлено у сотень речовин – чистих металів та металевих сплавів.
Температура переходу в надпровідний стан, те ператур ю перех ду Ткр,.
1.6. Явище надпровідності
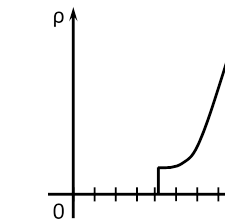
яка називається критичн ю
У 1986 - 1987 рр. було відкрито високотемпературну надпровідність керамічних провідників. Температура такого переходу відповідає температурі 120 К, що є нижчою від температури кипіння рідкого азоту. Якщо будуть розроблені надпровідники такого типу з достатньою міцністю, то можна буде передавати електроенергію на будь-які відстані без втрат.
Більше того, як показали дослідження, надпровідність не вичерпується тільки оберненням в нуль електричного опору провідника (ідеальною провідністю). Не менш цікавою властивістю речовини в надпровідному стані є ідеальний діа агнетиз . Ця властивість, відкрита Мейсснером і Оксенфельдом в 1933 р., полягає в тому, що речовина, поміщена в магнітне поле, при переході в надпровідний стан не «заморожує» магнітне поле, що знаходиться в ньому, як це повинно б було бути при простому переході речовини в стан з нульовим опором, а виштовхує його з свого об'єму. Це явище одержало назву ефекту Мей нера – Ок енфельда. Саме завдяки цьому явищу одне з головних застосувань надпровідників зв'язано з одержанням дуже сильних магнітних полів.
про публікацію авторської розробки
Додати розробку