ФОРМУВАННЯ ІНФОРМАЦІЙНО-ЦИФРОВОЇ КОМПЕТЕНТНОСТІ В УЧНІВ БАЗОВОЇ ШКОЛИ У НАВЧАННІ МАТЕМАТИКИ
Урок систематизації та коригування знань
(підготовка до контрольної роботи)
Тема: Натуральні числа.
Мета: систематизувати одержані знання учнів про читання і запис, порівняння і зображення натуральних чисел на координатному промені, а також про кути і їх вимірювання; коригувати знання і вміння учнів з метою підготовки їх до тематичної контрольної роботи; формувати інформаційно-цифрову компетентність.
Тип уроку: повторення, систематизації і корекції знань.
Обладнання: підручник [47], роздатковий матеріал, проектор, ноутбук, лінійка, транспортир.
Хід уроку
I. Організаційний момент.
ІІ. Актуалізація знань.
учням пропонується виконати усні вправи 1 - 4; їх можна дібрати, враховуючи помилки, яких припустились учні під час виконання самостійних робіт
Завдання 1. Виконайте усно вправи, подані на слайдах 1-4 (рис. 6-9).
учні зачитують по черзі, а у разі потреби виконують колективно

Рис. 6. Слайд № 1
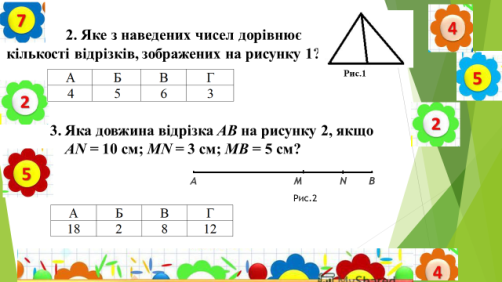
Рис. 7. Слайд № 2

Рис. 8. Слайд № 3

Рис. 9. Слайд № 4
IІI. Систематизація знань учнів. Відпрацювання вмінь і навичок.
пропонуються завдання, які диктуються вчителем або заздалегідь підготовлені на дошці, або виконуються із підручника чи роздаткового матеріалу – карток; послідовне виконання цих завдань можна провести у формі напівсамостійної роботи з поетапною перевіркою результатів, їх аналізом і корекцією виявлених учителем помилок (все це направлене на формування математичної та ІЦК учнів)
Завдання 2. (вчитель диктує)
усі учні записують у зошитах, учитель проходить і перевіряє; третю частину обговорюють
1) Запишіть числа:
а) два мільйони вісімдесят сім тисяч сорок дев’ять;
б) чотири мільйони триста дев’яносто три тисячі п’ятсот дванадцять.
2) Порівняйте записані числа. Яке з цих чисел лежить на координатному промені ліворуч? Зробіть відповідний запис.
3) Замініть першу цифру числа такою, щоб:
а) знак нерівності не змінився;
б) знак нерівності змінився на протилежний?
Завдання 3.
вчитель диктує; один учень виконує біля дошки, а інші – у зошиті; після виконання – порівнюють результати; обговорюють, якщо є розбіжності
1) Побудуйте координатний промінь і позначте на ньому одиничний відрізок, що дорівнює 1 см. Позначте на промені точки, які відповідають числам 2; 5; 9. Яка з точок лежить між двома іншими?
2) Порівняйте числа. Результат запишіть у вигляді подвійної нерівності.
3) Назвіть усі натуральні числа, що лежать між числами 2 і 9 на координатному промені. Як це можна записати?
Завдання 4. За готовим рисунком на дошці (рис.9).
один учень біля дошки виконує, потім усі звіряються і обговорюють, якщо є розбіжності
![]()
A C D B
Рис. 9. Відрізки.
1) Перемалюйте рисунок (рис. 9) у зошит. Запишіть усі відрізки, які ви бачите на цьому рисунку. Виміряйте лінійкою довжини відрізків AC, CD, BD, АD, BC, АВ. Зробіть відповідні записи.
2) Будемо вважати, що на рисунку (рис. 9) АС = 6 км, BD = 3 967 м. Порівняйте відрізки АС і BD.
Завдання 5.
- Виконайте усно № 143 з підручника [47].
- Що таке бісектриса кута?
- Чи зображена на рисунку 88 у підручнику [47] бісектриса? Через які числа треба провести промінь, щоб отримати бісектрису кута ВОК?
-
Яка градусна міра
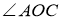 ,
, 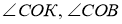 ? Зробіть відповідні записи.
? Зробіть відповідні записи.
Завдання 6.
це завдання записане на карточках (рис. 10), які учитель роздає по одній на парту; після самостійного виконання учні обговорюють результат у парах, а потім порівнюють відповіді із записом на дошці

Рис. 10. Картка «поділ кута».
Завдання 7. Виконайте усно завдання, подане на слайді 5 (рис. 11).

Рис. 11. Слайд № 5
Завдання 8. (додаткове № 40 підручника [47]).
№ 40. Знайдіть закономірність і запишіть два наступні числа:
- 1, 3, 5, 7, …; 3) 5, 12, 19, 26, …;
- 2, 4, 6, 8, …; 4) 800, 400, 200, 100, … .
ІV. Підсумки уроку.
важливо, щоб учні мали можливість висловити свою думку, обґрунтувати її та реально оцінити рівень своїх математичних знань і умінь, а також навичок роботи з різними джерелами інформації; учитель повинен оцінити роботу учнів на уроці
- Вправа «Моє враження»:
– я все зрозумів (зрозуміла), тому що …
– я частково зрозумів (зрозуміла), тому що …
– я нічого не зрозумів (зрозуміла), тому що …
- Оцінювання учнів
учитель виставляє оцінки тим учням, які виконували завдання на дошці, а також тим, які найменше допустили помилок або зовсім їх не допустили при самостійному виконанні у зошиті; також звертає увагу учнів, що отримані оцінки будуть внесені до електронного журналу класу
V. Домашнє завдання
- Дати відповіді на запитання у підручнику [47] – сторінка 48.
- Виконати тестові завдання [47] – сторінка 49.
В Україні створено електронні ресурси для підтримки освітян, які сприяють розвитку і вдосконаленню їх професійної компетентності та підвищенню кваліфікації. На цих ресурсах учителі мають змогу обмінюватися своїм педагогічним досвідом, обговорювати проблеми, які реально виникають у повсякденній роботі з учнями. Оскільки автор магістерської роботи на даний момент працює вчителем початкових класів (стаж роботи 6 років), а досвіду роботи з учнями базової школи майже немає (лише проходження педагогічної практики й інколи заміна вчителя математики у 5 класі), то для розробки наступного конспекту частково використовувалися матеріали з електронних ресурсів naurok.com.ua [35] та vseosvita.ua [44], а також посібника «Я і моя математика: Заочні математичні студії для школярів» [56], розробленого колективом викладачів та студентів кафедри математики та методики навчання математики ЧНУ ім. Б. Хмельницького.
Усі матеріали, використані для розробки конспекту другого уроку, направлені на активізацію навчально-пізнавальної діяльності учнів, сприяють формуванню предметних і ключових компетентностей, зокрема ІЦК, оскільки передбачають роботу з різними засобами навчання та інформацією, представленої у різних формах.
Урок відпрацювання практичних умінь і навичок
Тема уроку: Дії з десятковими дробами.
Мета: закріпити практичні навички і вміння учнів під час виконання завдань на десяткові дроби; ознайомити з історичною довідкою про дроби; активізувати навчально-пізнавальну діяльність учнів на уроці; зацікавити до вивчення матеріалу; формувати інформаційно-цифрову компетентність учнів.
Тип уроку: відпрацювання практичних умінь інавичок.
Обладнання: проектор, ноутбук, роздатковий матеріал.
Хід уроку
І. Організаційний момент.
1) Перевірка домашнього завдання.
учні порівнюють свої відповіді та заздалегідь підготовлені записи відповідей на дошці
2) Гра «Четверте зайве».
потрібно встановити, яке слово або число зайве в заданому наборі
Математика, фізика, торгівля, економіка.
1000; лікоть; 0,3; вісім.
Градус, транспортир, метр, миля.
![]() .
.
ІІ. Актуалізація знань.
- Цікаві повідомлення про десяткові дроби.
повідомлення учнями та вчителем історичних та цікавих фактів про десяткові дроби готувалися вдома, використовуючи підручник з математики, книги з шкільної бібліотеки, мережу Інтернет та інші джерела інформації (наводимо лише деякі з них)
Учень 1. У підручнику [47, с. 262-263] сказано, що десяткові дроби пов’язані з десятковою системою числення. Проте їхня поява має більш давню історію і пов’язана з ім’ям видатного математика й астронома ал-Каші (повне ім’я – Джемшид ібн-Масуд ал-Каші). У праці «Ключ до арифметики» (ХV ст.) він уперше сформулював правила дій з десятковими дробами, навів приклади.
Але нічого не знаючи про відкриття ал-Каші, удруге «відкрив» десяткові дроби приблизно через 150 років фламандський математик та інженер Сімон Стевін. У праці «Децималь» (1585 р.) С. Стевін виклав теорію десяткових дробів. Він усіляко пропагував їх, підкреслюючи зручність десяткових дробів для практичних обчислень.
Учень 2. Відокремлювати цілу частину десяткового дробу від дробової ал-Каші і С. Стевін пропонували по-різному. Так, ал-Каші цілу й дробову частини писав різними чорнилами або ставив між ними вертикальну риску. С. Стевін відокремлював частини десяткових дробів нулем у кружечку. Прийняту у наш час кому запропонував у 1592 році відомий німецький астроном Йохан Кеплер (1571 – 1630).
Нині в деяких країнах, наприклад у США, замість коми використовують крапку. У зв’язку з стрімким розвитком програмування використання крапки стає все популярнішим. Пригадайте, де ми використовуємо крапку під час запису десяткових дробів!
на слайді учні показують портрети згаданих науковців (рис.12)

Рис. 12. Портрети науковців.
Учень 3. Щоб не повторювати інформацію з підручника, здійснювався пошук цікавої інформації у мережі Інтернет. Зокрема, використавши джерело [10], хочу ознайомити клас із стародавніми мірами довжини, які були пов’язані з десятковими дробами (інформаціє подається на слайді презентації, рис. 13).

Рис. 13. Стародавні міри довжини.
Учитель. Чи задумувалися ви про те, які величини можуть позначати десяткові дроби? Наприклад (використано з [20]), дріб 0,001 – це на перший погляд невелике число (0,001 секунди – для нас у повсякденному житті це дуже мало). Але потяг зі швидкістю 72 км/год за цей час проїде 20 см; звук у повітрі пройде 33 см, а куля пролетить 70 см; Земна куля за це й же час проходить шлях по своїй орбіті навколо Сонця завдовжки 30 м; навіть комар встигає змахнути крилами вгору і вниз.
Дріб 0,000001 ще менший. Але для сучасного фізика-дослідника 0,000001 секунди – це зовсім немалий проміжок часу. Так, промінь світла за цей час пробігає 300 м.
Міліметр – це 0,001 м, що вдвічі менше від товщини сірника, однак для вимірювання хімічних процесів і реакцій це число є достатньо великим. Тут використовують мікрон – це 0,001 мм. Мікрон в 1000 раз менший від міліметра. Так звані червоні кров’яні тільця, яких у краплині крові близько 10 000 000, мають довжину 7 мк і товщину 2 мк. Усе в природі відносне і навіть числа.
- Математичний диктант.
вчитель швидко зачитує речення (без повторень), а учні повинні записати в зошит лише пропущене в реченні слово
- Результатом дії додавання є …
- Результатом дії множення є …
- Суму кількох однакових доданків можна замінити дією…
- Якщо один із доданків зменшити на три, то сума … на три.
- Якщо один із множників зменшити у k-разів, то добуток …
- Якщо знаменником правильного дробу є кругле число, то такий дріб називається …
- Ціла і дробова частини десяткового дробу відокремлюється …
- Один міліметр – це … частина сантиметру.
-
Між дробами 0,1 і
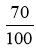 можна поставити знак …
можна поставити знак …
- Якщо ціла частина десяткового дробу дорівнює нулю, то він менший від …
ІІІ. Відпрацювання вмінь і навичок.
- Виконайте тестові завдання.
вчитель роздає бланки із завданнями, в яких треба обрати одну правильну відповідь, перші три учні, які правильно виконають усі завдання, можуть отримати 10 балів (матеріал використано із [56])
-
Запишіть у вигляді десяткового дробу 3
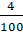 .
.
|
А |
Б |
В |
Г |
Д |
|
0,304 |
3,4 |
3,04 |
3,004 |
0,34 |
- Обчисліть 2,43 + 1,16.
|
А |
Б |
В |
Г |
Д |
|
3,59 |
2,59 |
6,82 |
3,45 |
4,38 |
- Обчисліть 4,67 – 2,34.
|
А |
Б |
В |
Г |
Д |
|
2,3 |
0,233 |
2,33 |
23,03 |
32,1 |
-
Як
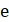 з чисел є коренем рівняння
з чисел є коренем рівняння 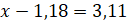 ?
?
|
А |
Б |
В |
Г |
Д |
|
1,93 |
4,3 |
0,429 |
4,29 |
3,2 |
-
Обчисліть 4,34 · 11,21

|
А |
Б |
В |
Г |
Д |
|
44,675 |
4,7654 |
44,876 |
7,8798 |
48,6514 |
- Знайдіть 0,2 від 45.
|
А |
Б |
В |
Г |
Д |
|
19 |
5 |
25 |
9 |
8 |
- Між якими двома сусідніми натуральними числами розміщується десятковий дріб 4,76?
|
А |
Б |
В |
Г |
Д |
|
2 і 3 |
3 і 4 |
4 і 5 |
5 і 6 |
7 і 6 |
- Знайдіть частку чисел 7,781 і 3,1.
|
А |
Б |
В |
Г |
Д |
|
1,2 |
2,18 |
2 |
2,815 |
2,51 |
- На скільки треба поділити число 58,88, щоб отримати число 2,56?
|
А |
Б |
В |
Г |
Д |
|
24 |
29 |
13 |
17 |
23 |
- У прямокутному паралелепіпеді висота дорівнює 6,7 см, довжина – 9,3 см, ширина – 4,2 см. Знайдіть об’єм паралелепіпеда.
|
А |
Б |
В |
Г |
Д |
|
120,765 |
775,43 |
261,78 см |
261,702 |
7,60 |
2. Виконання завдань зі слайду (рис.14).
учнів розподілили на чотири групи, кожна група виконує завдання свого варіанта
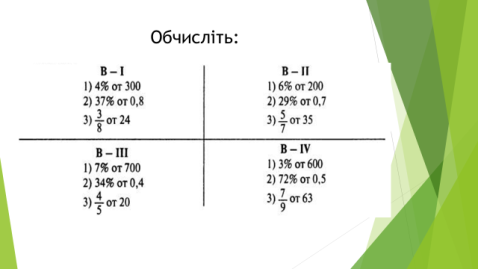
Рис. 14. Варіанти завдань.
3. Знаходження невідомого елемента у вигляді гри «Ланцюжок».
учні виходять по черзі до дошки, називають невідомий елемент дії та виконують одне завдання; першого учня викликає учитель, а потім цей учень називає наступного, хто вийде до дошки і т.д.
![]()
![]()
4. Гра «Магічний квадрат» (рис. 15) [20] .
учням треба встановити залежність і заповнити порожню клітинку квадрата
І – відповідь «2,6» (кожне з чисел зменшуємо на 0,5)
ІІ – відповідь «72,433» (по черзі додаємо 0,3; 0,03; 0,003)
ІІІ – відповідь «0,1» (кожне число ділимо на 4»
IV – відповідь «12» (кожне число множимо на 2)
V – відповідь «0,754» (кожне число ділимо на 10)
VI – відповідь «2» (кожне число множимо на 2)
І ІІ ІІІ
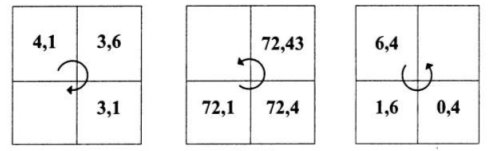
ІV V VI
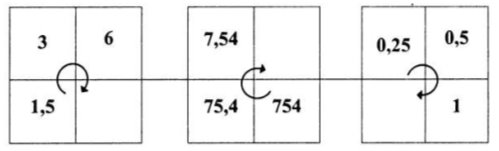
Рис. 15. Магічний квадрат.
IV. Підсумки уроку.
важливо, щоб учні мали можливість висловити свою думку, обґрунтувати її та реально оцінити рівень своїх математичних знань і умінь, а також навичок роботи з різними джерелами інформації; учитель повинен оцінити роботу учнів на уроці
- Вправа «Моє враження»:
– я все зрозумів (зрозуміла), тому що …
– я частково зрозумів (зрозуміла), тому що …
– я нічого не зрозумів (зрозуміла), тому що …
- Оцінювання учнів
учитель виставляє оцінки тим учням, які активно працювали протягом уроку і за тест; також звертає увагу учнів, що отримані оцінки будуть внесені до електронного журналу класу
V. Домашнє завдання.
1) Виконати завдання з підручника [Тарасенкова-5]: №№ 1416, 1443, 1483, 1489.
2) Скласти два власних «магічних квадрати» або кросворд на 10 запитань, пов’язаних з десятковими дробами
для підказки або у разі виникнення утруднень при створенні кросворда можна скористатися електронним ресурсом [40]
ВИСНОВКИ
(дописую)
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
- Бібік Н. В. Компетентнісний підхід: рефлексивний аналіз. Компетентнісний підхід у сучасній освіті: світовий досвід та українські перспективи: Бібліотека з освітньої політики. Київ: «К.І.С.», 2004. С. 45-50.
- Благодир Л. А. Інформаційно-цифрова компетентність учителя як складова професійної компетентності. URL: http://dspace.udpu.edu.ua/jspui/ bitstream/6789/10237/1/T_Blagodyr_L.pdf (дата звернення 01.10.2019).
- Богатирьова І. М. Застосування прийомів посилення розвивальної функції задач в курсі математики 5-6 класів. URL: http://enpuir.npu.edu.ua/bitstream/ 123456789/6738/1/Bogatyreva.pdf (дата звернення 11.11.2019).
- Вікіпедія. Вільна енциклопедія. URL: https://uk.wikipedia.org/wiki/%D0 %9A%D0%BE%D0%BC%D0%BF%D0%B5%D1%82%D0%B5%D0%BD%D1%82%D0%BD%D1%96%D1%81%D0%BD%D0%B8%D0%B9_%D0%BF%D1%96%D0%B4%D1%85%D1%96%D0%B4 (дата звернення 17.06.2019).
- Власій О. О., Дудка О. М. Шляхи формування інформаційно-цифрової компетентності учасників освітнього процесу. Open educational e-environment of modern University, special edition, 2019. С. 383-397.
- Генсерук Г. Р. Цифрова компетентність як одна із професійно значущих компетентностей майбутніх учителів. Відкрите освітнє е-середовище сучасного університету, 2019. URL: http://nbuv.gov.ua/UJRN/oeeemu_2019_6_4 (дата звернення 24.11.2019).
- Глобін О. І., Бурда М. І., Васильєва Д. В., Волошена В. В., Вашуленко О. П., Мацько Н. Д., Хмара Т. М. Компетентнісно орієнтована методика навчання математики в основній школі. Київ: Педагогічна думка, 2015. 245 с.
- Грицька Т. С. Етапи формування та види інформаційних компетентностей учнів. Комп’ютер у школі та сім’ї, 2010. №1. С. 41-42.
- Гуревич Р. С. Формування інформаційної компетентності майбутніх учителів засобами мультимедійних технологій. Наукові записки. Серія: Педагогіка, 2007. С. 38-41.
- Де в житті застосовуються дроби. URL: http://www.myshared.ru/slide/ 1162781/ (дата зверення 28.03.2019).
- Загальні методи навчання. URL: http://studentam.net.ua/content/ view/2271/97/ (дата звернення 30.10.2019).
- Закон України «Про освіту» (від 05.09.2017). URL: https://bit.ly/2BBxM8z
Загальні методи навчання. URL: http://studentam.net.ua/content/view/2271/97/ (дата звернення 30.10.2019).
- Запорожцева Ю. С. Інформаційно-цифрова компетентність як складник сучасного навчально-виховного процесу URL: http://www.innovpedagogy.od.ua/ archives/2019/12/part_1/17.pdf (дата звернення 23.07.2019).
- Зварич Н. Д. Формування ключових компетентностей на уроках математики шляхом залучення учнів до активної пошуково-пізнавальної діяльності. URL: http://navigator.rv.ua/wp-content/uploads/2019/02/Zvarych-N.D.Metodychna-rozrobka.pdf (дата звернення 19.08.2019).
- Зимняя И. А. Ключевые компетенции - новая парадигма результата образования. Высшее образование сегодня, 2003. № 5.
- Иванов Д. А. Компетенции и компетентностный подход в современном образовании. Завуч для администрации школ, 2008. № 1.
- Істер О. С. Математика. 5 кл. : підруч. для закл. заг. серед. освіти. Київ: Генеза, 2018. 288 с.
- Істер О. С. Математика : підруч. для 6-го кл. загальноосвіт. навч. закл. Київ: Генеза, 2014. 296 с.
- Класифікація методів навчання. URL: https://studfile.net/preview/5319195/ page:2/ (дата звернення 30.09.2019).
- Конспект уроку математики. URL: https://naurok.com.ua/urok-z-matemati ki-5kl-di-z-desyatkovimi-drobami-115604.html (дата звернення 13.03.2019).
- Когут Л. М. Формування цифрової компетентності в умовах інноваційного розвитку освітнього середовища закладів загальної середньої освіти. URL: http://klovsky77.com.ua/23-naukova-robota/225 (дата звернення 01.12.2019).
- Красільнікова О. Компетентнісний підхід як основа філософії освіти. Вісник КНТЕУ, 2018. №1. С.147-156. URL: http://visnik.knteu.kiev.ua/ files/2018/01/14.pdf (дата звернення 19.10.2019).
- Кузьмінський А. І. Педагогіка вищої школи. Київ: Знання, 2005. 486 с.
- Липова Л. І., Павлюк Л. Р. Формування математичних компетентностей учнів на уроках математики. Методичний пошук вчителя математики: зб. наук. праць за матеріалами ІІ Всеукр. дистанц. наук.-практ. конф., 18 жовтня 2018 р. Вінниця, 2018. С. 163-168.
- Лукьянова А. В. Особенности формирования информационной компетентности на этапе школьного образования. Ярославский педагогический вестник, 2014. №2. Том II. URL: http://vestnik.yspu.org/releases/2014_2pp/20.pdf (дата звернення 30.11.2019).
- Малик Ю. В. Використання активних методів навчання на уроках математики. URL: http://vspu.edu.ua/science/art/a205.pdf (дата зверення 11.10.2019).
- Мерзляк А. Г., Полонський В. Б., Якір М. С. Математика. 5 клас : підруч. для закладів загальної середньої освіти. Харків: Гімназія, 2018. 272 с.
- Мерзляк А. Г., Полонський В. Б., Якір М. С. Математика : підруч. для 6 кл. загальноосвіт. навч. закл. Харків: Гімназія, 2014. 400 с.
- Методи, прийоми навчання. URL: https://www.slideshare.net/ SvetlanaLyashenko/ss-56641407 (дата звернення 29.10.2019).
- Миронова О., Карпова Л. Формування інформаційної компетентності студентів як умова ефективного здійснення інформаційної діяльності. URL: http://www.stattionline.org.ua/pedagog/104/17664-formuvannya-informacijno%D1 %97-kompetentnosti-studentiv-yak-umova-efektivnogo-zdijsnennya-informacijno% D1%97-diyalnosti.html (дата звернення 23.10.2019).
- Мультимедійна дошка на уроках математики в 5-6-х класах. URL: https://mathlessons.ucoz.com/publ/jak_provesti_efektivnij_urok_na_temu_quot_vidsotki_quot/1-1-0-6 (дата звернення 07.09.2019).
- Навчальні програми для 5-9 класів. URL: https://mon.gov.ua/ ua/osvita/zagalna-serednya-osvita/navchalni-programi/navchalni-programi-5-9-klas (дата звернення 16.09.2019).
- Нoва українська шкoла. Концептуальні засади реформування середньої школи. URL: https://www.kmu.gov.ua/storage/app/media/reforms/ukrainska-shkola-compressed.pdf (дата звернення 03.09.2019).
- Овчарук О. В. Інформаційно-комунікаційна компетентність як предмет обговорення: міжнародні підходи. Комп’ютер у школі та сім’ї, 2013. С. 3-6.
- Освітній проект «На Урок». URL: https://naurok.com.ua/ (дата звернення 12. 03.2019).
- Пєтухова Л. Є. Інформатична компетентність майбутнього фахівця як педагогічна проблема. Комп’ютер у школі та сім’ї, 2000. С. 41-45.
- Пилипенко В. Ю. Використання інтерактивних технологій для активізації пізнавальної діяльності учнів на уроках математики. URL: https://www.schoollife.org.ua/809-2018/ (дата звернення 27.10.2019).
- Пометун О. І. Теорія та практика послідовної реалізації компетентісного підходу в досвіді зарубіжних країн. Компетентнісний підхід у сучасній освіті: світовий досвід та українські перспективи. Бібліотека з освітньої політики. Київ: «К.І.С.», 2004. С. 15-24.
- Проект Державного стандарту базової середньої освіти. URL: https://nus.org.ua/news/mon-rozrobylo-novyj-derzhstandart-bazovoyi-serednoyi-osvity/ (дата звернення 26.10.2019).
- Ребуси українською. URL: rebus1.com/ua/index.php?item=rebus440028 (дата звернення 28.03.2019).
- Рекомендації 2006/962/ЄС Європейського Парламенту та Ради (ЄС). URL: https://zakon.rada.gov.ua/laws/show/994_975 (дата звернення 10.09.2019).
- Савченко О. Я. Компетентнісний підхід як ресурс інноваційного розвитку шкільної освіти. Науковий вісник Ізмаїльського державного гуманітарного університету, 2015. С. 161-167. URL: http://nbuv.gov.ua/UJRN/Nvidgu_2015_33_36 (дата звернення 18.08.2019).
- Скакунова Г. В., Мороз І. О. Формування інформаційно-цифрової компетентності учнів з фізики через призму STEM-освіти. URL: https://cyberleninka.ru/article/n/formuvannya-informatsiyno-tsifrovoyi-kompetentnosti-uchniv-z-fiziki-cherez-prizmu-stem-osviti/viewer (дата звернення 13.10.2019).
- Спільнота активних освітян «Всеосвіта». URL: https://vseosvita.ua/ (дата звернення 30.11.2018).
- Сучасна освіта. URL: https://osvita.ua/school/method/780/ (дата звернення 26.10.2019).
- Тарасенкова Н.А. Компетентнісний підхід у навчанні математики: теоретичний аспект. Математика в рідній школі, 2016. №11. С.26-30.
- Тарасенкова Н. А., Богатирьова І. М., Бочко О. П., Коломієць О. М., Сердюк З. О. Математика. 5 кл. : підруч. для закладів загальної середньої освіти. Київ: Видавничий дім «Освіта», 2018. 240 с.
- Тарасенкова Н. А., Богатирьова І. М., Коломієць О. М., Сердюк З. О. Математика : підруч. для 6 класу загальноосвіт. навч. закл. Київ: Видавничий дім «Освіта», 2014. 304 с.
- Тарасенкова Н. А., Бурда М. І., Богатирьова І. М., Коломієць О. М., Сердюк З. О. Перевірка предметних компетентностей. Математика 5кл. Збірник завдань для оцінювання навчальних досягнень учнів. Київ: Оріон, 2016. 48 с.
- Тарасенкова Н. А., Бурда М. І., Богатирьова І. М., Коломієць О. М., Сердюк З. О. Перевірка предметних компетентностей. Математика 6кл. Збірник завдань для оцінювання навчальних досягнень учнів. Київ: Оріон, 2016. 52 с.
- Тренінг для педагогів «Компетентнісний підхід до освітнього процесу як вимога сучасності». URL: https://vseosvita.ua/library/trening-dla-pedagogiv-kompetentnisnij-pidhid-do-osvitnogo-procesu-ak-vimoga-sucasnosti-5519.html (дата звернення 24.09.2019).
- Українська педагогіка. URL: http://ukped.com/matematyka/129-.html (дата звернення 30.10.2019).
- Формування інформаційної компетентності учнів в умовах творчого використання інформаційно-технологічних методів навчання. URL: https://naurok.com.ua/formuvannya-informaciyno-kompetentnosti-uchniv-v-umovah-tvorchogo-vikoristannya-informaciyno-tehnologichnih-metodiv-navchannya-129005.html (дата звернення 10.11.2019).
- Формування інформаційної компетентності учнів на уроках математики. URL: https://vseosvita.ua/library/formuvanna-informacijnoi-kompetentnosti-na-urokah-matematiki-11625.html (дата звернення 22.10.2019).
- Хуторской А. Ключевые компетентности как компонент личностно ориентированной парадигмы образования. Народное образование, 2003. №2. С. 58-64.
- Я і моя математика: Заочні математичні студії для школярів. Матеріали для самопідготовки учнів 5 класу. За заг. ред. Н. А. Тарасенкової. Ч. 5. Черкаси: ФОП Гордієнко, 2018. 16 с.


про публікацію авторської розробки
Додати розробку
