ФОРМУВАННЯ У МОЛОДШИХ ШКОЛЯРІВ ЗДАТНОСТІ ОРІЄНТУВАТИСЯ НА ПЛОЩИНІ ТА У ПРОСТОРІ В УМОВАХ КОМПЕТЕНТНІСНОГО ПІДХОДУ (на прикладі першого класу)

Департамент освіти і науки виконкому Криворізької міської ради

КЗ “Центр професійного розвитку педагогічних працівників” КМР

Криворізька гімназія №41 Криворізької міської ради

 

 

 

 

 

 

ФОРМУВАННЯ У МОЛОДШИХ ШКОЛЯРІВ ЗДАТНОСТІ ОРІЄНТУВАТИСЯ НА ПЛОЩИНІ ТА У ПРОСТОРІ В УМОВАХ КОМПЕТЕНТНІСНОГО ПІДХОДУ

(на прикладі першого класу)

 

 

 

 

 

 Автор: Мушик Лілія Анатоліївна,

       учитель початкових класів

           e-mail: lmushi4ka@gmail.com

 

 

 

 

 

 

ЗМІСТ

 

ВСТУП…………………………………………………………………...………….  3

РОЗДІЛ 1. ТЕОРЕТИЧНІ ОСНОВИ ДОСЛІДЖЕННЯ

1.           Геометричний аспект предметної математичної компетентності молодшого школяра……………………………………………………………………     4
2.           Аналіз змістової лінії початкового курсу математики «Просторові відношення. Геометричні фігури» нової української школи під керівництвом О.Я. Савченко …...………………………………………….   9
3.           Психологічний аспект авторської програми А.Е. Сімановського з

розвитку просторового мислення дітей 6-12 років………………..……..   12

РОЗДІЛ 2. МЕТОДИЧНІ ОСНОВИ ФОРМУВАННЯ ЗДАТНОСТІ УЧНІВ ПЕРШОГО КЛАСУ ДО ОРІЄНТАЦІЇ НА ПЛОЩИНІ ТА В ПРОСТОРІ

 2.1. Завдання на словесний опис просторових відношень……………..……….. 17

 2.2. Завдання на переміщення і розміщення предметів у двовимірному

просторі …..…………………………………………………………….…………...24

ВИСНОВКИ …………………………………………………………………….     30

СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ ………………………….………..     33

ДОДАТКИ

Додаток А…………………………………………………………………………...34

Додаток Б.…..……………………………………………………………………….39

Додаток В…...……………………………………………………………………….42

ВСТУП

         Впровадження компетентнісного підходу у шкільну, зокрема початкову, освіту в Україні поставило багато нових завдань як перед науковцями, так і перед вчителями-практиками. Одне із основних завдань - як сприяти становленню компетентного учня в парадигмі компетентнісної освіти, яка є особистісно-діяльнісною результативною освітою. Вона зміщує акцент на здатність людини діяти в конкретному значенні контексті. Це знайшло відображення у новому Державному стандарті початкової загальної освіти нової української школи (галузь «Математика») та у новій редакції програми під керівництвом О.Я. Савченко з математики для 1-2 та 3-4 класів. У цих документах чітко і ґрунтовно означена предметна математична компетентність та її складові: обчислювальна, інформаційно-графічна, логічна, алгебраїчна і геометрична. А також визначені у державних вимогах до рівня загальноосвітньої підготовки учнів математичні компетенції, через які формується предметна математична компетентність.

       Здатність учня до орієнтації на площині та в просторі розглядається як компонент геометричної складової предметної математичної компетентності. Компетенції, через які формується вище вказана здатність, перелічені у змістовій лінії «Геометричні фігури», вивчення якої розпочинається з першого класу. Таким чином Міністерство освіти і науки України звернули увагу на результати досліджень психологів і педагогів з питань готовності дітей 6-річного віку до сприймання просторових відношень і форм. Аналіз програм для дошкільних закладів показує необхідність і доцільність такого підходу з метою забезпечення неперервності між дошкільною і початковою ланками освіти у формуванні умінь дітей орієнтуватися в двовимірному та тривимірному просторах.

  

 

 

 

 

РОЗДІЛ 1

ТЕОРЕТИЧНІ ОСНОВИ ДОСЛІДЖЕННЯ

1.           Геометричний аспект предметної математичної компетентності молодшого школяра

  Реалізацією компетентнісного підходу у шкільну, зокрема початкову, освіту зобов’язує вчителя початкових класів розуміти і осмисленно володіти базовими поняттями компетентнісною освіти: компетентнісний підхід, компетентність і компетенція (математичні); ключові і предметні (математичні) компетентності.

Дослідники компетентнісної освіти визначають компетентнісний підхід як напрям освітнього процесу, спрямований на формування і розвиток ключових і тематичних компетенцій. У результаті цього процесу мають бути сформовані загальні компетентності, які є інтегративними характеристиками результатів  навчання учнів. Компетенції набуваються в результаті навчання, особистої обізнаності та життєвого досвіду. Компетентність – це певна здатність, якою володіє учень [13].

Теоретичні засади з'ясування сутності понять «компетенція» і «компетентність», визначення структури компетентності, класифікації компетентностей тощо висвітлено в наступних публікаціях науковців України таких як: Т.М. Байбара,  Н.М. Бібік , С.П. Бондар , О.І. Локшина, , О.Я. Савченко та ін..

Як зауважує академік О.Я. Савченко найбільш поширеними є такі тлумачення «компетентності» і «компетенції».

Компетентність -  це загальна здатність особистості, яка набувається в процесі навчання. Це пояснюється тим, що компетентність включає в себе знання, навички, вміння, досвід, цінності та ставлення, які можуть бути комплексно застосовані на практиці.

Під компетентністю розуміється коло проблем, які людина повинна усвідомлювати, або конкретна область діяльності, до якої у людини повинні бути

здібності. Компетентність-це об'єктивна категорія, соціально визнаний рівень знань, навичок і взаємин у конкретній сфері людської діяльності. [13, С.13].

Сьогодні, завдяки тривалим академічним дебатам, зрозуміло, що поняття компетентності має чотири основні характеристики. Ці чотири риси є наступними:

•          Використання здібностей завжди здійснюється в певних ситуаціях (наприклад, у певних навчальних ситуаціях);
•          компетентність – це завжди результат, який описуєте, що людина може робити, а не пояснює чи розповідає про процес набуття цієї компетентності (наприклад, учні не кажуть «я читаю, я пишу», а показують, що вони можуть робити);
•          вимірювання компетентності особи вимагає чітко визначених і затверджених критеріїв;
•          компетентність – це міра того, що людина може зробити за певний час.

Як зазначає завідувач лабораторії початкової освіти Інституту педагогіки України, канд. пед. наук О.В. Онопрієнко - член авторського колективу з розробки Державного стандарту початкової загальної освіти (освітня галузь «Математика»), предметна компетенція формується в процесі засвоєння змісту навчальних предметів , зокрема математики. Тобто вони вважаються соціально закріпленими результатами навчання і представлені державними стандартами (розділи "Зміст освіти "і "Орієнтовні вимоги до академічної успішності учнів") і вказані в навчальному плані (стовпці таблиці "Зміст навчання" і "Очікувані результати навчання учнів") [9, С.47].

При визначенні предметних компетентностей та їх кількості необхідно розрізняти такі компоненти змісту освіти: реальні об'єкти, загальнокультурні знання про реальність об'єкта вивчення, загально-навчальні вміння і навички та способи діяльності.

У змісті початкового курсу математики множини та геометричні об'єкти класифікуються як реальні об’єкти.

  Знання загальної культури сучасної дійсності, елементів предметної освіти в змісті викладання математики.

  Знання математики, термінів, виразів, понять, законів та залежних відносин відображає форму.

   До термінів відносяться: одноцифрові числа, доданок, сума, чисельник, знаменник тощо.

Уявлення: натуральний ряд чисел, числовий вираз і його значення, рівняння з однією змінною, довжина, відстань, периметр, розташування об’єктів на площині і в просторі тощо.

Поняття: десяток, задача, розряди і класи чисел, дріб, площа фігури.

Закони: переставний і сполучний закони додавання і множення, розподільний закон множення.

 Залежності: між компонентами і результатом арифметичних дій, між швидкістю, часом і відстаню тощо.

       Властивості: частки, прямокутника.

       Вище зазначені компоненти на початкових етапах математичних знань є основними будівельними блоками більш складних навченостей, які учні здобувають протягом вивчення математики в початковій школі.

       Ці математичні знання застосовуються у відповідних способах діяльності. Навчання способом виконання дій-це процес формування загальних навчальних навичок. Уміння характеризує здатність учня виконувати певну діяльність та використовувати раніше набутий досвід на основі отриманих знань.

       Під час вивчення математичних об’єктів формуються розумові та практичні здібності учнів, передбачені державним стандартом початкової загальної освіти та представлені у вигляді математичних умінь і навичок:

"визначати периметр багатокутника і площі фігури, застосовувати формулу при обчисленні периметра і площі прямокутника", "моделювати відношення

різницевого і кратного порівняння чисел", "називати, читати, записувати, порівнювати числа в межах мільйона на основі десяткової системи числення" і т.д. [5, с.10]. Очевидно, що, називаючи предметні компетентності, автори враховували комплексний характер компетентностей.

Засвоєння  предметних компетентностей є ключовою основою для формування математичної компетентності.

         Поняття "математична компетентність" на сучасному етапі розвитку педагогіки визначається як ключова, так і компетентна здібності .У європейських рекомендаціях математична компетентність прирівнюється до фундаментальної природничо-наукової і технологічної компетентності та є ключовою. У документі «Ключові компетентності для навчання впродовж життя» це визначено так: «Математична компетентність — це здатність використовувати додавання, віднімання, множення, ділення та пропорцію в усних і письмових обчисленнях у повсякденних ситуаціях». Математична компетентність включає  в реальному світі  здатність використовувати математичні методи мислення (логічне та просторове) та мислення (формули, моделі, структури, графіки, діаграми)»  [8, С.189].

      Думка  більшості педагогів і, зокрема думку О.В. Онопрієнко, Л.П. Кочиної та Н.П. Листопад, які зауважують, викладання початкового курсу математика має особливе значення, яке відрізняє її від інших предметів. Тому правильно вважати, що математика формує елемент ключових компетентностей критичного мислення, відкриттів і суджень. Різні способи розв'язання навчальних проблем; створення алгоритмів для виконання дій; розподіл часу для роботи (навчальні навички); аналіз і відбір даних та інформації, необхідних для розв'язання проблем; застосування інформаційно-комунікаційних технологій для виконання творчої роботи; вибудовувати зв'язок висловлювань з використанням математичних  термінів (комунікація); працювати і взаємодіяти з групами, колективами (суспільство) і т.д. Таким чином, цілі і наслідки навчання

математики молодших школярів визначаються як предмет розвитку математичних здібностей [13].

У Державному стандарті початкової загальної освіти під математичною компетентністю з предмета слід розуміти уміння учня створювати математичну модель закономірностей навколишніх предметів і застосовувати отримані знання математичної компетентності для розв’язування навчальної, пізнавальної та практичної задачі. Це особистісне утворення, що містить в собі різноманітні психічні процеси, інтелектуальні та практичні навички, а також психологічні особливості - мотивацію, самостійність, самоконтроль, відповідальність, впевненість в собі [5].

      На основі наукових досліджень О.М.Леонтьєва,  А.В.Тихоненка, Ю. Трофименко членами авторского колективу з розробки Держстандарту є навички та способи виконання повсякденних завдань:

- вміння розраховувати;

- вміння використовувати інформацію, представлену в різних формах;

- вміння аналізувати, синтезувати та узагальнювати дані;

- вміння обчислювати довжину, площу та об'єм реальних об'єктів.

       Згідно з цим описом переліку, складовими математичної компетентності є обчислювальна, інформаційна, графічна, логічна та геометрична компетентності,  які розглядаються як внутрішні ресурси математичної компетентності.  

       Геометрична складова проявляється у власності з  просторовою уявою, просторовими відношеннями (визначення положення об'єктів на площині та в просторі, розміщення та переміщення об'єктів на площині); вимірюванням (визначення довжини та визначення площі навколишніх реальних об'єктів,  геометричні фігури) та конструкторські навички (малювання геометричних фігур на папері в клітинку, складання прямокутників, конструювання геометричних фігур з інших фігур, поділ фігур на частини).

Сьогодні, як зазначає Н.П.Листопад, геометричні знання в діяльності людини набувають особливого значення і застосовуються в найрізноманітніших галузях, включаючи хімію, фізику, астрономію, географію, архітектуру, будівництво та мистецтво. Уроки геометрії, що викладаються в початковій і середній школі, закладають міцний фундамент для подальшого професійного розвитку фахівців у галузі застосування геометрії. Елементарні навички з геометрії є  обов'язковими, і геометрія викладається в рамках навчальної програми початкової школи.

Мета введення елементів геометрії в молодших класах – підготувати учнів до систематичного навчання в основній школі, дати їм можливість використовувати знання та навички, набуті з інших предметів, для розв'язання проблем у житті.

У новому Державному стандарті початкової загальної освіти нової української школи передбачені, з позицій компетентнісного підходу, вимоги до результатів навчання учнів елементам геометрії. Це знайшло відображення у формульовані вимог до оцінювання знань учнів у змістовій лінії «Геометричні фігури»

2.           Аналіз змістової лінії початкового курсу математики «Просторові відношення. Геометричні фігури» під керівництвом О.Я.Савченко

      У новому Державному стандарті початкової загальної освіти нової української школи під керівництвом О.Я. Савченко (освітня галузь «Математика»), зазначено, що геометрична складова математичних здібностей заснована на умінні орієнтуватися у просторі, навичках вимірювання і проєктування, а також умінні застосовувати ці навички в життєвих ситуаціях [5].

       Аналізуючи чинні програми з математики для початкових класів показується,  що учні початкової школи мають оволодіти такими геометричними вміннями (компетентностями):

•          визначати розташування об'єктів на площині та у просторі:
•          розташовувати та змінювати положення об'єктів на площині та у просторі;
•          розпізнавати об’єкти навколишнього середовища за описом їхньої форми;
•          визначати геометричні фігури за їхнім описом;
•          розпізнавати форму об'єкта;
•          розпізнавати тип фігури;
•          описувати фігури (виділяти суттєві ознаки);
•          вибирати, класифікувати, розташовувати та візуалізувати фігури за заданими ознакам;
•          компонувати фігури (відрізки, прямокутники, кола);
•          досліджувати властивості геометричних перетворень та їх застосування;
•          застосовувати лінійку, циркуль і косинець для побудови геометричних фігур.

         Як слушно зауважує член авторського колективу з розробки оновленого Держстандарту початкової загальної освіти (надалі Держстандарт) з галузі

«Математика» Н.Листопад : «Визначені вміння є необхідною, але не достатньою умовою оволодіння предметом геометрії. Уміння застосовувати ці навички в потрібний час у реальних життєвих ситуаціях є важливим для учнів. [8, С.53]. Мова йде про потребу в оновленні початкової освіти, яка повинна бути компетентнісною - особисто - діяльнісною, результативною. Вона повинна забезпечити формування діяльної компетентної особистості. Рушійною силою відновлення статусу держави стала нагальна потреба оновлення системи освіти.

         У новому документі державні вимоги до загальної математичної підготовки учнів (результатів навчання) сформульовано з урахуванням компетентнісного підходу до оцінювання. Державними вимогами до загальної підготовки учнів у процесі оволодіння змістом матеріалу змістової лінії «Геометричні фігури» передбачені такі очікувані результати:

•          класифікувати фігури за їхніми характеристиками;
•          визначати складові частини геометричних фігур;
•          будувати геометричні фігури за допомогою лінійки,
•          будувати прямокутники;
•          використовувати латинські літери для позначення геометричних фігур;
•          комбінувати фігури;
•          ділити фігури на частини за певними критеріями;
•          розпізнавати геометричні фігури та їх елементи  у просторі;
•          співвідносити зображення геометричних фігур з  об'єктами навколишнього середовища.

       Посилаючись на думку академіка О.Я.Савченко, зазначимо, що формування змісту навчання за умов компетентнісного підходу відбувається «від результату»,  тобто від тих компетенцій, які повинні бути сформовані в учня. Тоді як в знаннєвій парадигмі освіти зміст навчання формувався «від мети».   

     Враховуючи результати досліджень психологів і педагогів, аналіз програм для дошкільних закладів освіти, експертні оцінки вчителів-практиків, які свідчили про доцільність ознайомлення молодших школярів з обʼємними геометричними фігурами, у новій програмі їх вивчення розпочинається з першого класу. Це фігури, які добре дітям відомі ще з дитячого садка - куля та куб.

        Під час ознайомлення з кулею та кубом бажано спиратися на конкретний життєвий досвід учнів. Розпочинати вивчення матеріалу рекомендується з аналізу моделей геометричних фігур. Наприклад, мʼяч, апельсин - це моделі кулі; коробка (що має форму куба), блок паперу для нотаток - це моделі куба. Ці тіла часто використовуються на уроках математики як дидактичний матеріал, що теж має позитивний вплив для їх засвоєння учнями.

        У подальшому вчитель пропонує учням завдання на розпізнавання цих тіл та спонукає учнів знаходити у навколишньому просторі предмети, що мають форму кулі та куба.

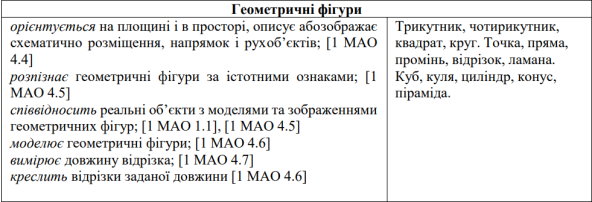
        Оскільки об’єктом дослідження є процес навчання математики учнів першого класу, то визначимо зміст навчального матеріалу та державні вимоги щодо рівня загальноосвітньої підготовки учнів першого класу у змістовій лінії «Просторові відношення. Геометричні фігури» під керівництвом О.Я. Савченко (див. табл. 1.1.)

Таблиця 1.1.

Виписка з програми курсу математики для першого класу.

Змістова лінія «Геометричні фігури» під

керівництвом О.Я. Савченко

3.           Психологічний аспект авторської програми А.Е. Сімановського з розвитку просторового мислення дітей 6-12 років

        Людина народжується і живе в тривимірному просторі. А тому досить

часто у процесі своєї діяльності зустрічається з необхідністю уявити зовнішній вигляд, структуру об’єктів навколишнього світу. Більшість професій - конструктор, архітектор, хірург, закрійник - вимагають від людини вміння мислено (в думці) виконувати просторові перетворення, добре орієнтуючись в просторі, видимому чи уявлюваному.

         Психологи довели, що починається розвиток просторових уявлень в ранньому дитинстві. Вже у трирічному віці діти легко розрізняють відкриті та закриті фігури і можуть правильно відтворити співвідношення розмірів двох кіл. У чотири роки діти вже вміють будувати пряму лінію із бусинок або ґудзиків, якщо для орієнтації побудови лінії дитині на допомогу кладуть паралельно лінійку або пропонують використати край столу. Перевіряючи, чи лінія пряма, дитина закриває одне око і проглядає напрям другим оком. При цьому вона шукає «точку зору», з якої добре видно «прямоту» лінії. У сім років діти вже добре розуміють, що один предмет може виглядати по різному з різних точок зору. Так, якщо семирічній дитині запропонувати розглянути конструкцію із кубиків і вибрати із декількох рисунків ті, які відповідають виду цієї конструкції збоку, зверху, спереду, то він легко це робить. До дев’яти - десяти років діти починають різні можливі перспективи. Це означає, що в цей віковий період діти, співставляючи три види проекцій об’єкта,  можуть представити його просторову модель і навчитися мислиннєво її трансформувати, що є безпосередньо завданням творчої уяви.

          Але навчання учнів просторовій мисленнєвій діяльності з просторовими образами пов’язане з багатьма труднощами. Одна із них - це невміння

молодшими школярами виділяти головне в задачі з геометричним змістом або в проблемній ситуації, пов’язаній з самостійним утворенням нового образу. В

силу цих обставин, образи, які виникають у свідомості дитини, можуть відходити від головної мети і не спонукати виявленню абстрактної залежності між уявленнями.

        Розв’язання цієї проблеми, на думку дослідника А.Е. Сімановського, залежить від засвоєння дитиною способів аналізу і перетворення просторових проблемних ситуацій. Оволодіння алгоритмами цих мисленнєвих операцій дозволяє дитині свідомо відноситися до мети і умови завдання, розуміти загальну логіку перетворення просторового обʼєкта.

        Останнім часом з’явилися нові навчальні курси для початкової школи, в яких робота з обʼємними фігурами і розгортками посідає належне місце.

Значна увага розвитку просторового мислення приділена в комплектах посібників М.І. Моро, Б.П. Гейдмана, Є.П. Бененсона, Л.П. Петерсон, Е.Г. Гельфмана та ін., а в методичному плані заслуговують на увагу наробки А.Е. Сімановського. Він є автором програми, реалізація якої сприяє формуванню в дитини навичок візуального мислення та уяви. Програма складається з шести частин, кожна з яких відповідає певному етапу багатоступеневої методики з розвитку просторого мислення дитини. У відповідності до предмета нашого дослідження для нас важливу роль відіграють перші два етапи. Охарактеризуймо їх більш детально.

       На першому етапі учні 6-7 років тренуються розуміти і позначати просторові відношення таких видів: попереду, позаду, вгорі, внизу, ліворуч, праворуч, над, під, через, за і т.д. На цьому етапі формується вміння створювати просторовий образ за словесним описом, мислено слідкувати і запам’ятовувати траєкторію руху обʼєкта, яка описана словами. Основна частина завдань першого етапу будується на основі двомірного простору. Тому основне завдання вчителя полягає в тому, щоб навчити учнів перетворювати словесний опис тривимірного простору в двовимірний зоровий образ. Як показують спостереження більшість дітей шести років розрізняють праву і ліву сторони,

вгору, вниз у реальному просторі, але не завжди можуть це зробити на аркуші паперу. Тому у процесі навчання учнів треба обов'язково ознайомити з прийнятими умовними позначеннями площинного зображення.

        У віці дев’яти - десяти років діти готові засвоїти правила перспективного зображення, що дає можливість їм розуміти і передавати за допомогою рисунку тривимірне зображення об’єктів. Велике (крупне) починає сприйматися ними як більш близьке, ніж мале (мілке), яке сприймається як далеке. Стає складнішою система орієнтацій і, відповідно, виникає необхідність у доповненні лексичного запасу, який дозволить точно передати місцезнаходження графічних об’єктів.

       На першому етапі також важливо відпрацьовувати вміння гнучко змінювати систему графічних орієнтирів у залежності від точки зору зображеного героя. Досить часто діти 6 років ототожнюють свою точку зору з точкою зору героя рисунку. Формування цієї здібності і перевірку її сформованості можна реалізувати за допомогою рисунків, на яких точка зору намальованого героя не співпадає з точкою зору художника. Наприклад, таким рисунком є зображення людини в анфас. Так, праву руку і ногу, зображеної в фас людини, шестирічні діти часто називають лівими і, відповідно, ліву руку і ногу - правими. До семи років діти повинні вже свідомо вибирати точку зору і з неї описувати простір рисунку. Для цього завдання підручників математики для першого класу (авт. М.В.Богданович, Л.П.Кочина, Н.П.Листопад) є необхідність доповнити завдання із посібника А.Е.Сімановського , в яких учням пропонується знайти ліву і праву сторони обʼєктивів з різних точок знаходження спостерігача. Це допоможе у реалізації державної вимоги до рівня загальноосвітньої підготовки учнів у процесі вивчення змістової лінії «Просторові відношення. Геометричні фігури» в умовах компетентнісного підходу. Учень повинен не розповідати як це треба зробити, а самостійно виконувати завдання на встановлення просторових відношень між предметами, розміщеними на площині та в просторі (лівіше, правіше, вище, нижче тощо).

        Другий етап (учні 7 років) передбачає навчання учнів виконувати завдання на переміщення і зміну обʼєктів в двовимірному просторі. На цьому етапі учні вчаться аналізувати структуру площини зображення, мислено змінюючи її. Тут можливі задачі на переміщення монет і сірників, задачі на переріз фігур, на обʼєднання (складання) фігур із частин. Завдання, які розвʼязують учні на другому етапі характеризуються різнотипністю і різним ступенем складності.

Складність завдання може бути зумовлена як кількістю можливих варіантів (сполук), які повинен перебрати учень для пошуку правильного розвʼязку, так і необхідністю відшукати нетрадиційний підхід до пошуку розвʼязання завдання.

        В основному завдання другого етапу розраховані на дітей семирічного віку, але ми поділяємо думку автора програми, що окремі завдання такі як «Танграм»,  завдання із паличками можуть успішно розвʼязувати і діти 6 років . У цілому завдання другого етапу підготовлюють дітей до розуміння закономірностей площинної геометрії, навчають бути спостережливими і формують творче відношення у роботі з геометричними обʼєктами.

         Третій етап цієї методики передбачає продовження роботи дітей у двовимірному просторовому зображенні. На цьому етапі формується вміння учнів працювати з координатною площиною, картою, шаховою дошкою.

Діти знайомляться з загальноприйнятими умовними позначеннями, які використовуються під час створення двохвимірних схем і вчаться їх читати.

Завдання цього етапу відповідають віковим особливостям дітей семи-восьми років. На цьому етапі учні отримують додаткові засоби для позначення місцезнаходження обʼєктів, які дозволяють йому відобразити точні координати довільної точки простору на схемі і спланувати траєкторію свого власного або

чужого руху. Такі уміння добре відпрацьовуються в іграх «Морський бій», «Шахи», «Шахмати». Отже, на даному етапі уміння і навички  орієнтуватися в графічному двовимірному просторі переходять на новий рівень розвитку.

        Слід звернути увагу, що програмою передбачено виконання завдань на мисленнєве обертання складних геометричних фігур, що є не завжди посильними для учнів восьми років, не говорячи про семирічних дітей. Але для реалізації цієї програми такі завдання є необхідними, оскільки вони підготовляють учнів до розвʼязування задач на перетворення обʼємних геометричних тіл, з якими учні будуть працювати на наступних етапах

програми.

      Четвертий етап передбачає навчання учнів працювати з зображеннями просторових фігур у тривимірному просторі. Вони навчаються за кресленням визначати довжину, ширину і висоту обʼємної фігури, аналізувати її структуру і

склад. При цьому діти навчаються мислено «бачити» обʼєкт з різних позицій: зверху, збоку, ззаду, спереду. На цьому етапі учні знайомляться з назвами обʼємних геометричних фігур і вчаться зображати їх на папері. Завдання четвертого, і наступних - пʼятого і шостого етапів методики розраховані на дітей віком девʼять - дванадцять років.

         П’ятий етап методики спрямований на вироблення вміння координувати види зображень на кресленні. У результаті виконання завдань цього етапу діти набувають навичок мислено конструювати обʼємний образ обʼєкта. У майбутньому ці базові вміння допоможуть учневі вільно, без затруднень «читати» креслення довільної складності.

       Шостий етап методики спрямований на розвиток умінь перетворювати об’ємні геометричні тіла. Для цього учням доцільно пропонувати завдання з перерізами і розгортками об’ємних фігур. Основою на цьому етапі виступає робота з предметними моделями. Виготовляючи моделі, учні вчаться мислено уявляти послідовність просторових перетворень, планувати власні «трудові» операції, творчо підходити до виконання роботи.

       У зв’язку з тим великим значенням, яке приділяється сьогодні реалізації геометричної складової предметної математичної компетенції молодших школярів в умовах компетентнісної освіти, описана вища авторська програма з розвитку просторового мислення дітей може бути використана, як пропедевтичний курс геометрії і креслення для учнів початкової школи за рахунок варіативної частини навчального плану. А також за цим варіантом програми можна проводити заняття курсу за вибором з окремою групою дітей, або індивідуальну роботу з учнями, які виявляють схильність і інтерес до дослідження, творчої діяльності.

 

 

 

 

 

 

 

 

 

РОЗДІЛ 2

МЕТОДИЧНІ ОСНОВИ ФОРМУВАННЯ ЗДАТНОСТІ УЧНІВ ПЕРШОГО КЛАСУ ДО ОРІЄНТАЦІЇ НА ПЛОЩИНІ ТА В ПРОСТОРІ

       Формування вміння орієнтуватися на площині та у просторі (як компонента геометричної складової предметної  математичної компетентності) відбувається через компетенції. Цей процес може бути реалізований на основі відповідної системи завдань, яка передбачає спосіб діяльності, адекватний особливостям суб'єкта, і здатна створити ситуацію, в якій учні набувають досвіду розв'язання практичних завдань і вмотивованого ставлення до процесу і результату розпізнавання.

Розглянемо, як першокласники можуть розв'язувати такі завдання. Переміщатися на площині або в просторі; знаходити предмети в просторі або на площині; самостійно встановлювати зв’язки між предметами у просторі; розташовувати предмети на площині та переміщувати їх у заданому напрямку; говорити, використовуючи відповідний синтаксис; визначати взаємне розташування навколишніх предметів.

2.1. Завдання на словесний опис просторових відношень

      Основне завдання для учнів 6-7 років полягає в тому, щоб сформувати уміння створювати просторовий образ за словесним описом, в думці стежити і запам’ятовувати траєкторію руху, яка описується на словах. Учні тренуються в розумінні і позначенні просторових відношень за допомогою слів і словосполучень: направо, наліво, через, за, під, над, вгору, вниз і т.д.

       Більшість завдань, які пропонуються учням для виконання на першому етапі базуються на основі двохвимірного рисунку. Тому дитина навчається

перекладати словесний опис тривимірного простору в двохвимірний зоровий образ. У цьому відношенні необхідним доповненням до завдань розміщених у підручниках математики - 1 кл. (авт. М.В.Богданович, Л.П.Кочина, Н.П.Листопад) виділяємо і рекомендуємо до обовʼязкового використання тематичне тестове завдання «Розміщення предметів на площині і в просторі» подане у посібнику «Тести з математики для 1 класу середньої загальноосвітньої школи» (авт. Л.П.Кочина), яке подається у додатку А.

       Окремі вміння цього етапу можуть бути сформовані вже у дітей

шестирічного віку, так як більшість із них добре розрізняють ліву і праву сторони, верх і низ у реальному просторі, але не завжди можуть це зробити на аркуші паперу. Тому навчання учнів на цьому етапі необхідно спрямувати на пояснення і усвідомлення ними, прийнятих в нашій культурі

домовленостей зображень на площині.

        У 6-7 річному віці головними проблемами є: орієнтація у графічному просторі листка аркуша; вміння «децентрирувати» і побачити картинку з чужої точки зору; мислено співвіднести між собою обʼєкти, які знаходяться у полі

характеристики обʼєкта. Завдання, які ми пропонуються на цьому етапі спрямовані на формування саме цих здібностей.

        Наведемо приклади таких завдань тут і далі в методичному супроводі для вчителя з тематичними тестовими завданнями «Розміщення предметів на площині і в просторі» подане у посібнику «Тести з математики для 1 класу середньої загальноосвітньої школи» (авт. Л.П.Кочина) [5].

Завдання 1. На рисунку зображені предмети - постав хрестики в тих місцях кімнати, де вони повинні бути розташовані, і зʼєднай хрестики і предмети стрілками (див. виконання завдання на рис. 2.1.1. і 2.1.2.)

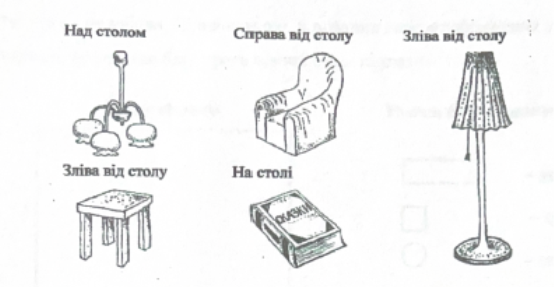
Рис.2.1.1.Картка – заготовка до завдання 1.

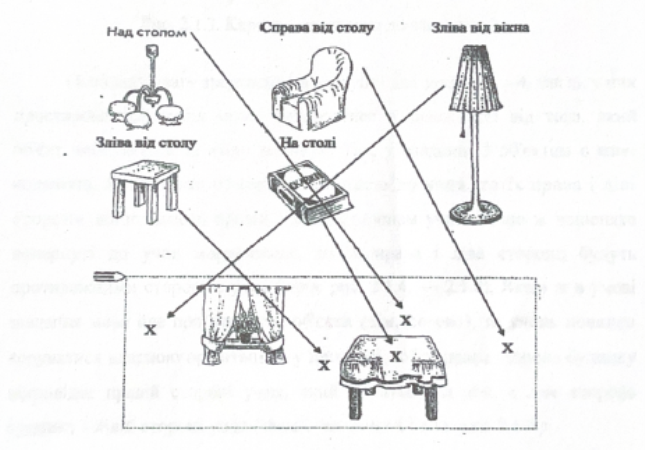
Рис.2.1.2. Зразок виконання завдання 1.

 

Завдання 2. Прочитай і покажи на схемі кімнати розташування меблів. Я ввійшов у велику квадратну кімнату і зупинився, зробивши два кроки.

       Справа біля стіни я побачив гарно вмонтований комод. Далі, вздовж стіни, стояло велике зручне крісло. Я обійшов масивний дубовий, круглий стіл і сів у це крісло. Піднявши очі, я побачив своє відображення у великому дзеркалі, яке стояло біля протилежної стінки кімнати.

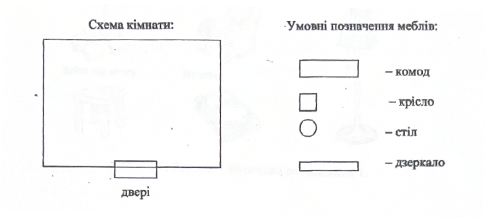
Рис.2.1.3. Картка – заготовка до завдання 2.

        Особливу увагу приділяємо наступним двом завданням 3-4, так як у них просторова орієнтація може відрізнятися в залежності від об’єкта та вибирається за «тіло відліку». Так, у завданні 3 обʼєктом є живі кошенята. Якщо вони повернуті спинкою до учня, то їх права і ліві сторони відповідають правій і лівій сторонам учня. Якщо ж кошенята повернуті до учня мордочками, то їх права і ліва сторони будуть протилежними сторонам учня ( див. рис. 2.1.4. — 2.1.8). Якщо ж в умові завдання мова йде про нерухомі обʼєкти (дім, дерево), то учень повинен керуватися власною орієнтацією у просторі, тобто права сторона будинку відповідає правій стороні учня, який дивиться на дім, а ліва сторона будинку - лівій стороні учня (читай завдання 4 і див. рис. 2.1.8.).

        Завдання 3. Жили були три кошенятка:

Рис. 2.1.4. Картка – заготовка до завдання 3.

       Вийшли кошенята на прогулянку. Рижик став справа від Біленького, а Черниш зліва. Розфарбуй рис.2.1.5. Не забувай, що права і ліва сторони кошенят можуть не співпадати з твоїми правою і лівою сторонами.

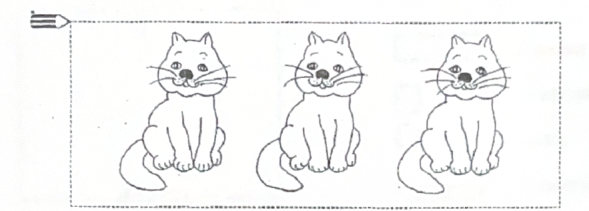
Рис. 2.1.5. Картка – заготовка для виконання завдання 3.

Відповідь: Рижик, Біленький, Черниш.

    Раптом кошенята побачили великого хруща, який сидів на землі. Вони підбігли до нього і стали його розглядати. При цьому Черниш був справа від Рижика і зліва від Біленького. Розфарбуй рис.2.1.6.

Рис. 2.1.6. Картка-заготовка для виконання завдання 3.

Відповідь: Рижик, Черниш, Біленький.

     Жук прикинувся не живим, став нерухомим, і кошенята втратили до нього інтерес, їх захопив шорох у траві, біля забору. Обережно підкравшись до цього місця, вони завмерли. Черниш знаходився зліва від Рижика, а Рижик зліва від Біленького. Розфарбуй рисунок 2.1.7.

Рис.2.1.7. Картка-заготовка для виконання завдання 3.

Відповідь: Біленький, Рижик, Черниш. Раптом трава розтягнулася, і на кошенят поглянула велика собача голова. Це був сусідський пес Полкан. Кошенята

злякались і побігли додому. А вдома їх вже чекали блюдця із свіжим молоком. Блюдце Біленького стояло зліва від блюдця Рижика і справа від блюдця Черниша. Розфарбуй рисунок 2.1.8.

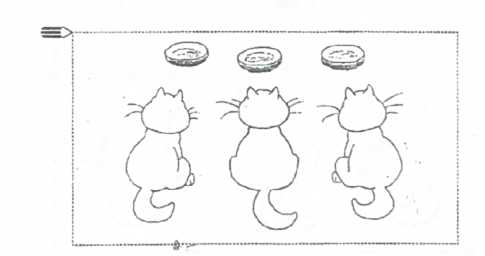
Рис.2.1.8. Картка-заготовка для виконання завдання 3.

Відповідь: Черниш, Біленький, Рижик.

 Завдання 4. Який берег є лівий, а який правим залежить від течії річки. Якщо стати обличчям по течії, то справа буде правий берег,  а зліва – лівий. Скарб закопали на правову березі річки зліва від будинку , але справа від дерева. Допоможи хлопчику знайти скарб і покажи те місце, де він заритий. (Напрям руху течії позначено стрілкою. Праві і ліві сторони хатинок і дерев оцінюються по відношенню до спостерігача).

 

Рис.2.1.9. Картка – заготовка до завдання 4.

            Розв’язуючи це завдання з учнями, учитель повинен допомогти дітям усвідомити той факт, що хлопчик змінює своє положення в навколишньому просторі і на малюнку зображено його положення після того, як він визначив, де правий берег річки, і тому він повернутий обличчям до правого берега, там де закопаний скарб (треба звернути увагу на стрілку, яка зображує напрямок течії річки). А потім шукати місце, де закопаний скарб, уявивши себе на місці хлопчика. Відношення «бути ліворуч» і «бути праворуч» від різних обʼєктів слід оцінювати у відношенні до себе як спостерігача, тобто як точки відліку.

Наступну групу завдань на словесний опис просторових відношень у методиці виділяють як графічні диктанти.

      Перша група: Приготуй олівець і зошит в клітинку. Постав точку на перетині вертикальних і горизонтальних ліній, відступивши 5-6 клітинок від верхнього і 1-2 клітинки від лівого краю листка. Це буде точка старту – точка А. Із точки А олівець може рухатися по лінії вправо, вліво, вгору, вниз. При цьому він може проходити одну, дві, три і більшу кількість клітинок. Наприклад, вчитель диктує: дві клітинки вгору, одна клітинка направо. Одна клітинка вгору, дві клітинки направо. Одна клітинка вниз. Одна направо. Дві направо. Одна вниз. Одна клітинка направо. Дві вниз.

         Друга група завдань графічного диктанту передбачає спочатку уважно вислухати диктування вчителя, уявити і запам’ятати конфігурацію узору і тільки після цього накреслити узор в зошит.

         Третя група завдань передбачає доповнення чотирьох вже знайомих

учням направлень руху ще чотирма рухами по діагоналі. Олівець може рухатися по діагоналі вправо вгору (а); вліво вгору (б); вправо вниз (в); вліво

вниз (г).

Рис.2.1.10. Нові направлення руху олівця по діагоналі.

       Четверта група - це завдання які треба виконати «подумки». Треба

уважно вислухати диктування вчителя, відповісти на яку цифру схожа одержана фігура і тільки після цього виконати побудову зображення, вважаючи, що стартова точка А знаходиться на другій зверху лінійці і 4 клітинки вправо від краю листа. Наприклад, вчитель диктує: по діагоналі вправо вгору одна клітинка. Одна клітинка вправо. По діагоналі вправо вниз одна клітинка. Одна клітинка вниз. По діагоналі вліво вниз три клітинки. Одна клітинка вниз. По діагоналі вправо вниз одна клітинка. Вправо одна клітинка. По діагоналі вправо вгору одна клітинка. Вгору одна клітинка. По діагоналі вліво вниз три клітинки. Одна клітинка вниз. По діагоналі вправо вниз одна клітинка. Вправо одна клітинка. По діагоналі вправо вгору одна клітинка. Вгору одна клітинка. По діагоналі вліво вгору три клітинки. Одна клітинка вгору.

2.2. Завдання на переміщення і розміщення предметів у двовимірному просторі.

        Завдання цього типу характеризуються як різнотипністю так і різним степенем складності. Складність зумовлена як кількістю можливих ходів або сполучень, які повинен перебрати учень для правильного розвʼязання задачі так і нетрадиційним підходом для пошуку можливих неоднозначних варіантів розвʼязання задачі. Бажано щоб на цьому етапі учні мали можливість діяти (працювати) з реальними предметами, випробовуючи різні варіанти переміщення і утворюючи нові розміщення на площині. Адже, на думку психологів, лише в 13-14 років діти спроможні виконувати такі перестановки мислено (в думках).

         З метою формування уміння працювати в двовимірному просторі учням доцільно пропонувати завдання на переріз площинних фігур, розміщення і переміщення паличок або монет.

Завдання 1. На рисунку зображено 12 монет. Приєднай до них ще дві

монети так, щоб утворилося 7 рядів по 4 монети у кожному ряді.

Рис.2.2.1. Заготовка до завдання 1.

        Для розв’язування цієї задачі доцільно мати 14 монет або їх зображень, щоб учень виконував практичні дії по приєднанню монет до заданих 12 і лічив утворені ряди по 4 монети у кожному.

         Можливі варіанти розв’язку:

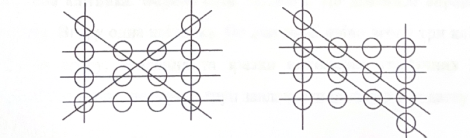
Рис.2.2.2. Варіанти розв’язання завдання 1.

    Завдання 2. Три палички лежать на столі. Як перемістити палички, щоб середня паличка стала крайньою, не перемішуючи їх.

                       

Рис.2.2.3. Заготовка до завдання 2.

        Для розв’язування задачі, щоб перебрати всі можливі варіанти, доцільно палички пронумерувати і тоді, можливо, показати варіанти: 2 – це середня паличка, вона може бути крайньою зліва і крайньою справа. На рис.2.2.4. подаються можливі варіанти переміщення.

Рис.2.2.4. Варіанти розв’язання завдання 2.

          Завдання 3. Із 10 паличок зробили ключ (див.рис.2.2.5.). Переклади в ньому 4 палички так, щоб отримати три квадрата.

 

     

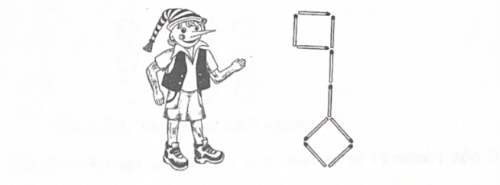
Рис.2.2.5. Заготовка до завдання 3.

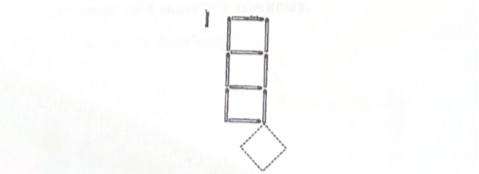
Рис.2.2.6. Варіант розв’язання завдання 3.

    Завдання 4. Рак із паличок повзе вгору (див.рис.2.2.7.). Переклади три палички так, щоб він поповз вниз.

   

Рис.2.2.7. Заготовка до завдання 4.

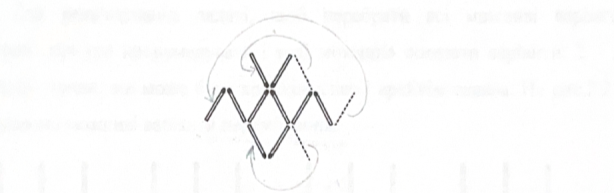
Рис.2.2.8. Варіант розв’язання завдання 4.

         Завдання 5. Склади фігурки тварин із восьми рівних трикутників, які ти отримаєш після розрізання квадрата.

  

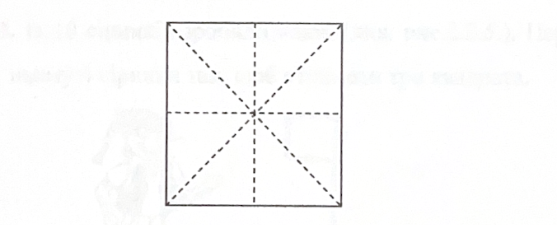
Рис.2.2.8. Заготовка до завдання 5.

        Для розвʼязання цієї задачі та гри «Танграм», яка  подається у додатку В, доцільно заздалегідь із цупкого паперу вирізати фігурки із яких треба буде скласти намальовані зображення. Маючи під рукою такий «допоміжний матеріал», учень зможе накладаючи частинки - фігури на зображення, знайти потрібний варіант комбінації їх.

   Якщо учень досить легко виконує завдання методом накладання, то йому можливо запропонувати діяти по-іншому. Нехай частинки - фігури лежать

осторонь, а учень подумки шукає місце для кожної частинки у зображенні. Дитина може користуватися олівцем, лінійкою і гумкою, для того, щоб він міг помічати лінії розрізів на зображенні і витирати їх гумкою в разі необхідності.

 

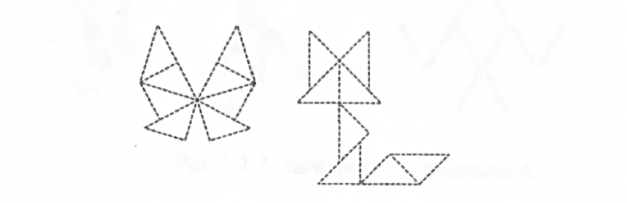
Рис.2.2.10. Варіанти розв’язання завдання 5.

       Великою популярністю серед учнів 6-7 років користуються завдання, для розв’язування яких необхідно порахувати кількість простих фігур у зображенні складеної. Для прикладу розглянемо завдання 6.

       Завдання 6. Скільки трикутників ти можеш знайти на рисунку?

 

 

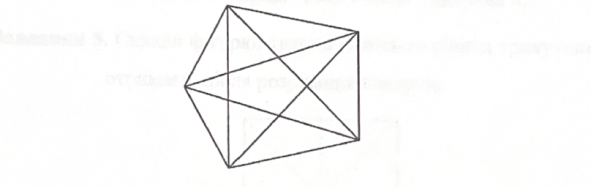
Рис.2.2.11. Заготовка до завдання 6.

Відповідь : 35 трикутників.

        У такому зображенні кількість вилучених трикутників перевіряти досить важко. Учні часто допускають типову для таких завдань помилку. Вони двічі, а інколи і тричі рахують один і той  трикутник. Щоб полегшити підрахунок трикутників у зображені складеної фігури доцільно запропонувати учням позначити всі точки перетину і зміни напрямку ліній буквами алфавіту. Це забезпечить можливість записати всі виділені трикутники і таким чином вилучити повтори.

        Молодші школярі полюбляють грати в шахи. Але це заняття можна перетворити на дослідження, коли учень буде з’ясовувати скільки варіантів

можна запропонувати, виконуючи самостійно практичні дії на переміщення  шахів на площині. Така діяльність в індивідуальній формі або робота в парах сприяє формуванню таких компетенцій учня першого класу як: «я знаю (вмію) як розмістити шахи на площині аркуша паперу», «я розміщую шахи у заданих напрямах», «я переміщую шахи у заданих напрямах», «я визначаю взаємне розміщення шахів».

         Завдання 7. Перестав шахи так, щоб виконувалися наступні умови

завдання і порахуй скільки буде усього можливих варіантів переміщення шахів.

На рисунку зображені дві білі і дві чорні шашки. Необхідно переставити білі шашки на місто чорних, а чорні на місто білих. При цьому необхідно дотримуватися таких умов:

- кожна шашка може перескочити на найближчу клітинку або через клітинку, але не далі;

- у кожній клітинці повинна бути тільки одна шашка;

- починати треба з білої шашки;

- не можна виконувати хід два рази підряд шахами одного кольору.

  

Рис.2.2.12. Заготовка до завдання 7.

Відповідь: 12 переміщень у такій послідовності:

Рис.2.2.13. Варіанти розв’язання завдання 7.

      Поповнити виділені завдання можна використавши посібник А.Е. Сімановського «Розвиток просторового мислення дітей» [33], який допоможе вчителю в організації самостійної діяльності учнів з формування основних компетенцій геометричної складової предметної математичної компетентності учнів початкових класів.

 

 

 

 

 

 

 

 

 

 

 

 

ВИСНОВКИ

        Перехід до компетентнісної освіти початкової ланки освітньої системи України відзначився початкової загальної освіти (галузь «Математика») та новим варіантом  програми під керівництвом О.Я. Савченко з математики для 1-2 та 3-4 класі.

        Авторським колективом, який працював над розробкою змістових ліній освітньої галузі «Математика» Держстандарту та програми з математики для 1-2, 3-4 кл. НУШ під керівництвом О.Я. Савченко висловлене узгоджене бачення сутності математичної компетентності молодшого школяра як предметної

компетентності та визначені її складові: обчислювальну, інформаційно-графічну, логічну, алгебраїчну, геометричну.

          Предметна математична компетентність формується через математичні компетенції.

         У змісті першого класу «Геометричні фігури» акцентується увага на геометричній складовій математичної компетентності, яка включає вміння: визначати положення об'єктів на площині та у просторі. Встановлювати відношення (наприклад, ліворуч, праворуч, вгору, вниз) між об'єктами на площині та у просторі. Розміщувати предмети на плоскій поверхні, наприклад, на папері або столі; переміщувати предмети в заданому напрямку (справа наліво, зліва направо, зверху вниз, знизу вгору); використовувати відповідний синтаксис у розмові; визначати взаємне розташування об'єктів навколо себе.

          Методика формування у молодших школярів здатності орієнтуватися на площині та у просторі, як складного особистісного утворення учня, ґрунтується на відпрацюванні способів дій у самостійній практичній діяльності з використанням практичного досвіду дитини, здобутого у відповідні сензитивні періоди дошкільного та молодшого шкільного віку.

        Дитина живе в тривимірному просторі і вчиться діяти і орієнтуватися в цьому з раннього дитинства. Тому така велика увага розвитку здатності учнів початкової школи орієнтуватися на площині та у просторі цілком виправдана і

 

результати досліджень науковців і методистів з цього питання знаходять свій вихід у практику роботи початкової школи через комплекти посібників

Є.П.Бененсон, Б.П.Гейдман, Е.Г.Гельфман, М.І.Моро, Л.П.Петерсон, А.Е.Сімановського та ін. Окремо слід вказати на тестові завдання для учнів першого класу, розроблені одним із авторів підручників з математики для 1-4 класів Л.П.Кочиною.

        У виявленій  програмі А.Е.Сімановського «Розвиток просторового

мислення дитини» реалізується багатоступенева методика (шість етапів)

навчання учнів 6-12 років мисленнєвій діяльності. Для учнів 6-7 років у цій програмі є два перші етапи: словесний опис просторових відношень та розвиток умінь працювати у двовимірному просторі. Ми їх адаптували з відповідності до реалізації державних вимог щодо рівня загальноосвітньої підготовки учнів з математики.

         Перший етап методики навчання учнів мисленнєвій діяльності з просторовими образами (6-7 років) реалізується у процесі навчання учнів розвʼязувати завдання на переклад словесної характеристики тривимірного простору в двохвимірний зоровий образ. Основними цілями цього етапу є: сформувати в учнів уміння створювати просторовий образ за словесним описом, в думці стежити і запам’ятовувати траєкторію руху, яка описується на словах і навпаки. Учні тренуються у розумінні і позначенні просторових відношень за допомогою слів і словосполучень: направо, наліво, через, за, під, над, вгору, вниз і т.д. Більшість завдань на даному етапі засновані на основі двохвимірного рисунку. Основна проблема, з якою зустрічаються учні в цей період, полягає в тому, що орієнтуючись у реальному просторі, учні не завжди можуть це зробити на аркуші паперу, а тому особливу увагу, під час навчання учнів розвʼязувати задачі вказаного виду, необхідно спрямувати на пояснення і усвідомлення учнями, прийнятих домовленостей зображень на площині.

         Результативність навчання учнів мисленнєвій діяльності (перший етап- учні 6-7 років) за описаною в розділі 2 методикою розвʼязування завдань на словесних опис просторових відношень та переміщення і розміщення предметів у двовимірному просторі може бути підтверджена тестуванням учнів за

тестовими завданнями «Розміщення предметів на площині і в просторі», розробленими кандидатом педагогічних наук Л.П. Кочиною.

           Враховуючи, що це лише перший етап навчання учнів мисленнєвій діяльності з просторовими образами,  сподіваюся, що при поетапному формуванні в учнів здатності до орієнтації у просторі, вчитель зможе забезпечити належний рівень її сформованості.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ

1. 1. Байбара Т. Компетентнісний підхід в початковій ланці освіти: теоретичний аспект. Початкова школа. 2010. № 2010. С. 46–50.

2. Бевз Г. Геометрія в загальноосвітній школі. Математика в школах України. 2003. № 2. С. 7–11.

3. Бібік Н. Компетентність і компетенції в результатах початкової освіти. Початкова школа. 2010. № 9. С. 2–5.

4. Про внесення змін до Державного стандарту початкової освіти. Офіційний вебпортал парламенту України. URL: https://zakon.rada.gov.ua/laws/show/688-2019-п#Text (дата звернення: 11.12.2024).

5. Кочина Л. Тести з математики для 1 класу середньої загальноосвітньої школи. 2-ге вид. Київ : КІМО, 2003. 64 с.

6. Листопад Н. Геометрична складова математичної компетентності молодшого школяра: сутнісна характеристика. Початкова школа. 2011. № 8. С. 51–54.

7. Онопрієнко О. Предметна математична компетентність як дидактична категорія. Початкова школа. 2010. № 10. С. 47.

8. Петерсон Л. Комплексний розвиток особистості учнів засобами математики. Початкова школа. 2002. № 5. С. 25–27.

9. Програми для середньої загальноосвітньої школи. 1-2 класи. Офіційний вебпортал Міністерсва освіти і науки України. URL:https://mon.gov.ua/staticobjects/mon/sites/1/zagalna%20serednya/programy-1-4-klas/2022/08/15/Typova.osvitnya.prohrama.1-4/Typova.osvitnya.prohrama.1-2.Savchenko.pdf 

10. Степанов О. Психологічна енциклопедія. Київ : Академвидав, 2006. 424 с.

11. Савченко О. Я. Компетентнісний підхід як чинник модернізації початкової освіти. Наука і освіта. Науково-практичний журнал Південного наукового центру НАПН України. Педагогіка. 2011. № 4. С. 13–16.

12. Савченко О. Я. Навчання і виховання учнів 1 класу: [методичний посібник для вчителів]. Початкова школа. 2002. С. 210–297.

13. Скворцова С. Обчислювальні навички як складова предметно-математичної компетентності молодшого школяра. Початкова школа. 2011. № 8. С. 48–51.

Додаток А .

Тематичне тестове завдання «Розміщення предметів на площині і в просторі» подане у посібнику «Тести з математики для 1 класу середньої загальноосвітньої школи» (авт. Л.П.Кочина).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

      Для оцінювання результатів виконання цих завдань автор Л.П.Кочина пропонує такий варіант виявлення рівня навчальних досягнень учня з розділу «Розміщення предметів на площині і в просторі»:

Таблиця А.1.

Оцінювання завдань тестів у балах

Номер завдання тесту	1	2	3	4	5	6	7	8	9	10	Усього балів
Кількість балів	1	1	1	1	2	3	3	4	5	5	26

Таблиця А.2.

Оцінювання навчальних досягнень учнів (НДУ)

Рівні НДУ	Високий	Достатній	Середній	Початковий
Кількість балів	26-22	21-17	16-10	9 і менше

 

Додаток Б

Завдання до графічних диктантів:

 

Завдання першого етапу

Приготуй олівець і зошит в клітинку. Постав точку на перетині вертикальних і горизонтальних ліній, відступивши 5-6 клітинок від верхнього і 1-2 клітинки від лівого краю аркуша. Це буде точка старту - точка А. із точки А олівець може рухатися по лінії вправо, вліво, вверх, вниз.

При цьому він може проходити одну, дві, три і більшу кількість клітинок.

а) Дві клітинки вверх. Одна клітинка направо. Одна клітинка вверх. Дві клітинки направо. Одна клітинка вниз. Одна направо. Дві клітинки вниз. Дві направо. Дві вверх. Одна направо. Одна клітинка вверх. Дві направо. Одна вниз. Одна клітинка направо. Дві вниз.

б) Дві клітинки вверх. Дві клітинки направо. Одна вниз. Одна клітинка направо. Одна клітинка вниз. Дві направо. Дві вверх. Дві направо. Одна вниз. Одна направо. Одна вниз. Дві клітинки направо.

На наступному занятті дітям пропонують спочатку уважно вислухати диктування вчителя, уявити і запам’ятати конфігурацію візерунка. Тільки після цього учні повинні намалювати візерунок у зошиті.

в) Дві клітинки вверх. Одна клітинка направо. Одна клітинка вверх. Одна направо. Дві клітинки вниз. Одна направо. Одна вниз. Дві клітинки направо. Дві вверх. Одна направо. Одна клітинка вверх. Одна направо. Дві вниз. Одна направо. Одна вниз. Дві направо.

г) Дві клітинки вверх. Дві направо. Одна вверх. Одна направо. Одна вниз. Одна направо. Дві клітинки вниз. Одна направо. Дві вверх. Дві направо. Одна вверх. Одна направо. Одна вниз. Одна направо. Дві вниз. Одна направо.

 д) Дві клітинки вверх. Одна наліво. Одна клітинка вверх. Три клітинки направо. Одна клітинка вниз. Одна клітинка наліво. Дві вниз. Три клітинки направо. Дві вверх. Одна наліво. Одна вверх. Три клітинки направо. Одна вниз. Одна наліво. Дві вниз. Три клітинки направо.

 е) Дві клітинки вверх. Одна клітинка наліво. Дві клітинки вверх. Одна клітинка направо. Одна вниз. Дві направо. Одна вниз. Одна наліво. Дві клітинки вниз. Три клітинки направо. Дві вверх. Одна клітинка наліво. Дві клітинки вверх. Одна клітинка направо. Одна вниз. Дві клітинки направо. Одна вниз. Одна наліво. Дві клітинки вниз. Три клітинки направо.

Завдання другого етапу:

а) Вниз 5 клітинок. Вправо 10 клітинок. Вверх 5 клітинок. По діагоналі вліво вверх 2 клітинки. Вверх 3 клітинки. Вліво 2 клітинки. Вниз одна клітинка. По діагоналі вліво вверх одна клітинка. По діагоналі вліво вниз 5 клітинок.

 б) По діагоналі вправо вниз 2 клітинки. Вправо 6 клітинок. По діагоналі вправо вверх 2 клітинки. Вліво 3 клітинки. По діагоналі вліво вверх 4 клітинки. Вниз 3 клітинки. Вліво 4 клітинки.

в) По діагоналі вправо вверх 2 клітинки. По діагоналі вправо вниз 2 клітинки. Одна клітинка вліво. По діагоналі вправо вниз 2 клітинки. Дві клітинки вліво. По діагоналі вправо вниз три клітинки. Три клітинки вліво. Дві клітинки вниз. Дві клітинки вліво. Дві клітинки вверх. Продовжити малюнок.

г) По діагоналі вправо вверх 3 клітинки. По діагоналі вправо вниз 3 клітинки. По діагоналі вліво вниз 3 клітинки. Вправо 5 клітинок. По діагоналі вправо вверх 4 клітинки. Вниз 6 клітинок. По діагоналі вліво вниз 3 клітинки. Вліво 6 клітинок. По діагоналі вправо вверх одна клітинка. По діагоналі вліво вверх 4 клітинки. По діагоналі вправо вверх 3 клітинки. Вліво 3 клітинки.

Наступні завдання учням пропонують виконати подумки. Для цього треба уважно вислухати диктування вчителя, відповісти, на яку цифру схожа фігура, яку отримують. Стартова точка А на другій зверху лінії, 4 клітинки вправо від краю аркуша.4 клітинки. По діагоналі вправо вверх 3 клітинки. Вліво 3 клітинки.

е) Вправо 2 клітинки. По діагоналі вліво вниз 2 клітинки. Вправо 2 клітинки. Вниз 2 клітинки. Вліво 2 клітинки.

ж) Вверх одна клітинка. Вправо 2 клітинки. Вниз 2 клітинки. По діагоналі вліво вниз 2 клітинки. Вправо 2 клітинки.

з) По діагоналі вправо вверх 1 клітинка. Одна клітинка вправо. По діагоналі вправо вниз одна клітинка. Одна клітинка вниз. По діагоналі вліво вниз 3 клітинки. Одна клітинка вниз. По діагоналі вправо вниз одна клітинка. Вправо одна клітинка. По діагоналі вправо вверх одна клітинка. Вверх одна клітинка. По діагоналі вліво вверх 3 клітинки. Одна клітинка вверх.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток В

Гра «Танграм»

З давніх часів люди грають в геометричну гру «Танграм». Ця гра захоплює і дітей і дорослих. Гра полягає у тому, що із 7 частин квадрату складають різні фігури людей, тварин, пташок.

 Перекресли квадрат на шматок картону або аркуш цупкого паперу. Розкресли його за зразком, який поданий на рисунку.

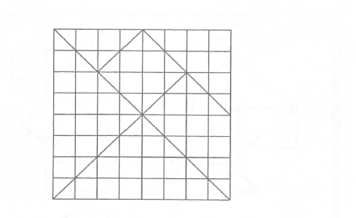
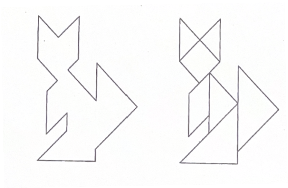
У результаті такого креслення і вирізування фігур повинні отримати: два великих рівні трикутника; один середній трикутник; два рівних маленьких трикутника; один квадрат і один паралелограм. Тепер ти можеш скласти із них фігури за зразками, які подані на рисунках.

Частини геометричних фігур повинні доторкатися одна одної , але не перекривати одна одну.