ГЕОМЕТРИЧНА ОПТИКА. СФЕРИЧНЕ ДЗЕРКАЛО
Про матеріал
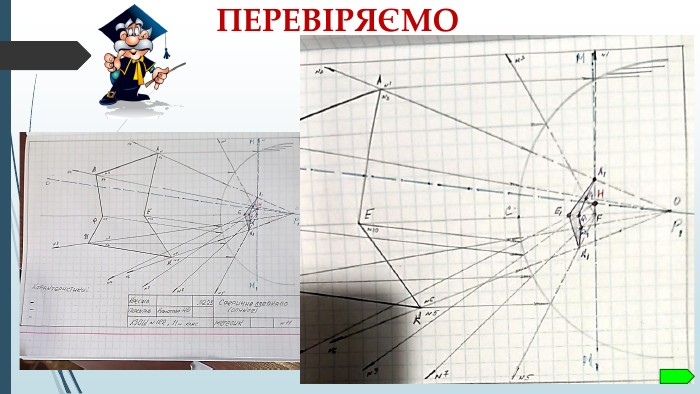
АЛГОРИТМ ПОБУДОВИ ЗОБРАЖЕННЯ У СФЕРИЧНОМУ ДЗЕРКАЛІ ЗАЗВИЧАЙ СКЛАДНО СПРИЙМАЄТЬСЯ УЧНЯМИ. ТОМУ КОЖЕН ПУНКТ АЛГОРИТМУ ВІДПОВІДАЄ ЕТАПАМ ПОБУДОВИ ЗОБРАЖЕННЯ.
КРЕСЛЕННЯ, ЯКІ ПРОПОНУЮТЬСЯ ДІТЯМ ДЛЯ РОБОТИ ВИКОНАНІ З УРАХУВАННЯМ ЕЛЕМЕНТІВ КРЕСЛЕННЯ. ПОПЕРЕДНЬО ДІТИ ОЗНАЙОМЛЕНІ З ЦИМИ ЕЛЕМЕНТАМИ. Перегляд файлу
Зміст слайдів
pptx
До підручника
Фізика (академічний рівень, профільний рівень) 11 клас (Бар’яхтар В.Г., Божинова Ф.Я., Кирюхіна О.О., Кірюхін М.М.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку















![Рефлектор прожектора являє собою угнуте сферичне дзеркало з радіусом кривизни R = 30 см. Визначити : на якій відстані l від фокуса дзеркала треба розташувати на головній оптичній осі точкове джерело світла, щоб одержати конічний пучок відбитих променів, що сходиться в точку на відстані L = 10 м від полюса дзеркала. ЗАДАЧА 1: ОFCSS1 HММ𝟏 PP1 ДАНО: CIR= 30 cм = 0,3 m. L = 10 м f = Ld = F + l_______L = ?Положення вершини відбитого пучка S1 і джерела S зв'язані формулою сферичного дзеркала Оскільки дзеркало угнуте і точка S1 є дійсним зображенням точки S, усі величини у формулі мають знак «+» Тому формула сферичного дзеркала здобуває вигляд: 𝟏𝑭+𝒍+ 𝟏𝑳= 𝟏𝑭 l = 𝑭𝟐𝑳−𝑭 , де F = 𝑹𝟐 l = 𝑹𝟐𝟐(𝟐𝑳−𝑹) З урахуванням того, що за умовою L >> R, остаточну відповідь доцільно представити у вигляді:l ≈ 𝑹𝟐𝟒𝑳 Перевіримо в одиницях: [l] = [м𝟐м] = м{l} ≈ 𝟎,𝟑 ·𝟎,𝟑 𝟒·𝟏𝟎≈ 2,25 ·𝟏𝟎 −з; l = 2 мм. Відповідь: l = 2 мм – відстань, на якій від фокуса дзеркала треба розташувати на головній оптичній осі точкове джерело світла Рефлектор прожектора являє собою угнуте сферичне дзеркало з радіусом кривизни R = 30 см. Визначити : на якій відстані l від фокуса дзеркала треба розташувати на головній оптичній осі точкове джерело світла, щоб одержати конічний пучок відбитих променів, що сходиться в точку на відстані L = 10 м від полюса дзеркала. ЗАДАЧА 1: ОFCSS1 HММ𝟏 PP1 ДАНО: CIR= 30 cм = 0,3 m. L = 10 м f = Ld = F + l_______L = ?Положення вершини відбитого пучка S1 і джерела S зв'язані формулою сферичного дзеркала Оскільки дзеркало угнуте і точка S1 є дійсним зображенням точки S, усі величини у формулі мають знак «+» Тому формула сферичного дзеркала здобуває вигляд: 𝟏𝑭+𝒍+ 𝟏𝑳= 𝟏𝑭 l = 𝑭𝟐𝑳−𝑭 , де F = 𝑹𝟐 l = 𝑹𝟐𝟐(𝟐𝑳−𝑹) З урахуванням того, що за умовою L >> R, остаточну відповідь доцільно представити у вигляді:l ≈ 𝑹𝟐𝟒𝑳 Перевіримо в одиницях: [l] = [м𝟐м] = м{l} ≈ 𝟎,𝟑 ·𝟎,𝟑 𝟒·𝟏𝟎≈ 2,25 ·𝟏𝟎 −з; l = 2 мм. Відповідь: l = 2 мм – відстань, на якій від фокуса дзеркала треба розташувати на головній оптичній осі точкове джерело світла](/uploads/files/1149321/342634/394939_images/16.jpg)