Графи. ПОШУК У ШИРИНУ ТА ГЛИБИНУ.

Графи. ПОШУК У ШИРИНУ ТА ГЛИБИНУЦодікова Л. М.

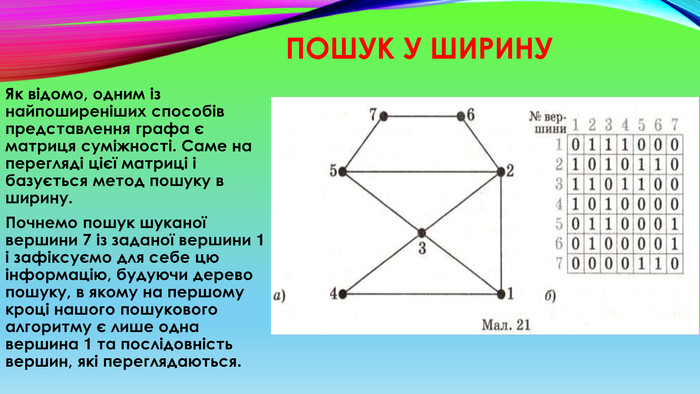
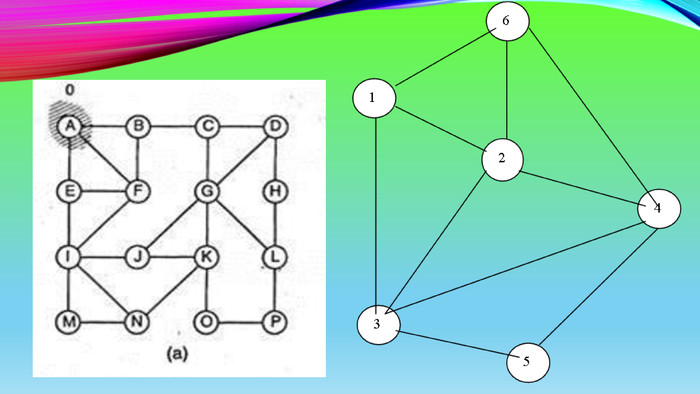
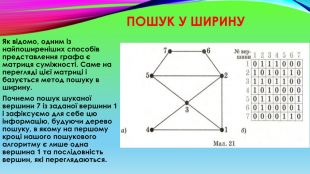
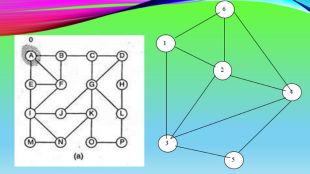
Пошук у ширину. Як відомо, одним із найпоширеніших способів представлен­ня графа є матриця суміжності. Саме на перегляді цієї матриці і базується метод пошуку в ширину. Почнемо пошук шуканої вершини 7 із заданої вершини 1 і зафіксуємо для себе цю інформацію, будуючи дерево пошуку, в якому на першому кроці нашого пошукового алгоритму є лише одна вершина 1 та послідовність вершин, які перегля­даються.

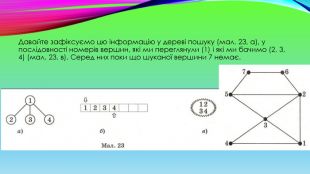
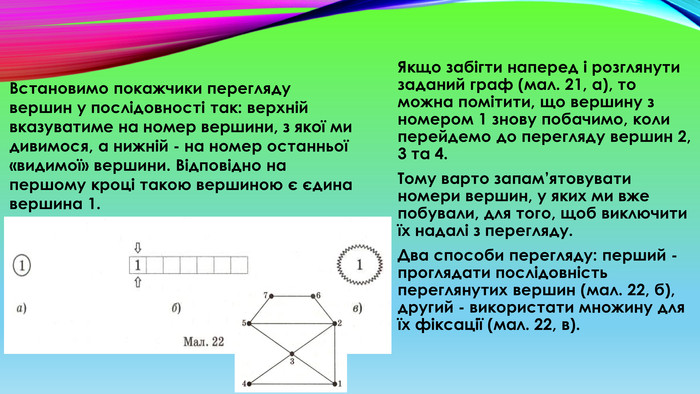
Якщо забігти наперед і розглянути заданий граф (мал. 21, а), то можна помітити, що вершину з номером 1 знову побачимо, коли перейдемо до перегляду вершин 2, 3 та 4. Тому варто за­пам’ятовувати номери вершин, у яких ми вже побували, для того, щоб виключити їх надалі з перегляду. Два спосо­би перегляду: перший - проглядати послідовність переглянутих вершин (мал. 22, б), другий - використати множину для їх фіксації (мал. 22, в). Встановимо покажчики перегляду вершин у послідовності так: верхній вказуватиме на номер вершини, з якої ми дивимося, а нижній - на номер останньої «видимої» вершини. Відповідно на першому кроці такою вершиною є єдина вершина 1.

Давайте зафіксуємо цю інформацію у дереві пошуку (мал. 23, а), у послідовності номерів вершин, які ми переглянули (1) і які ми бачимо (2, 3, 4) (мал. 23, в). Серед них поки що шуканої вершини 7 немає.

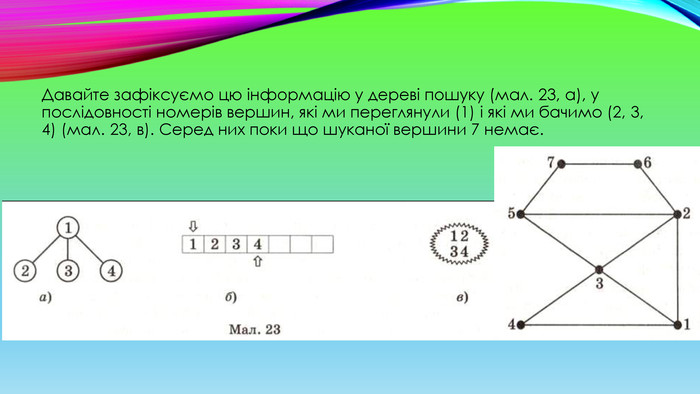
Для подальшого пошуку перейдемо до однієї з нових вершин, які ми побачили. Це вершини 2, 3 і 4. У нашій послідовності (мал. 23, б) першою записана вершина 2, тому й перейдемо до неї. З вершини 2 бачимо верши­ни 1, 3, 5 і 6. Лише вершини 5 і 6 є новими, а вершини 1 і 3 ми вже бачили на попередніх кроках нашого алгоритму. Доповнимо дерево пошуку.

У послідовності ми ще не дісталися шуканої вершини 7, тому переходимо у послідовності вершин до на­ступної «побаченої» вершини 3, яку тепер можна буде назвати не лише «побаченою», але ще й «переглянутою». Згідно із зобра­женням графа і відповідної йому таблиці суміжності з вершини З ми бачимо вершини 1, 2, 4 і 5. Але вони не є новими, тому ми їх не фіксуємо ні у дереві пошуку, ні у послідовності вершин, ні у множині (мал. 25, а, б, в).

З вер­шини 4 ми знову-таки нічого нового не побачимо, оскільки вершини 1 та 3 ми вже бачили раніше.

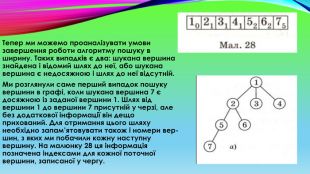
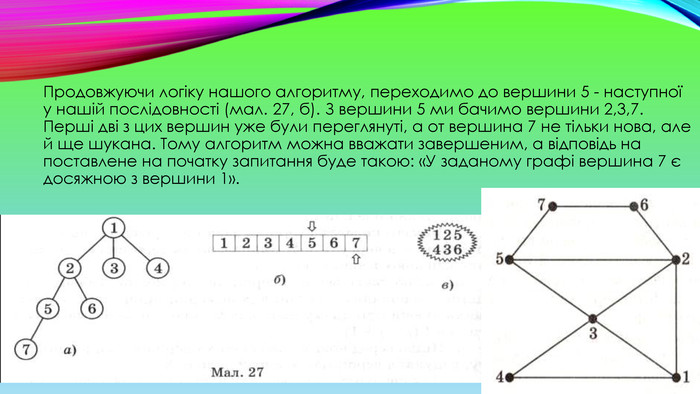
Продовжуючи логіку нашого алгоритму, переходимо до вер­шини 5 - наступної у нашій послідовності (мал. 27, б). З верши­ни 5 ми бачимо вершини 2,3,7. Перші дві з цих вершин уже бу­ли переглянуті, а от вершина 7 не тільки нова, але й ще шука­на. Тому алгоритм можна вважати завершеним, а відповідь на поставлене на початку запитання буде такою: «У заданому графі вершина 7 є досяжною з вершини 1».

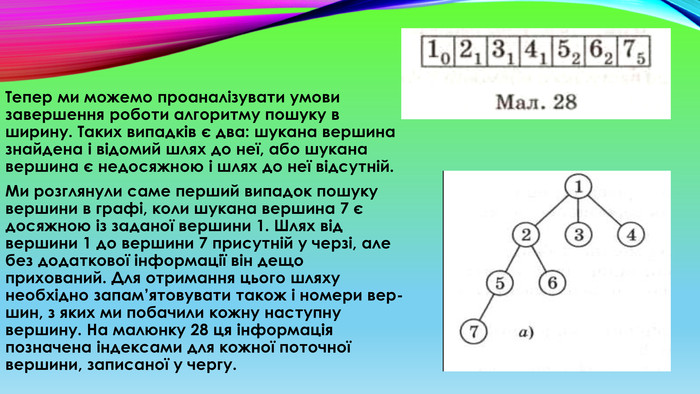
Тепер ми можемо проаналізувати умови завершення роботи алгоритму пошуку в ширину. Таких випадків є два: шукана вершина знайдена і відомий шлях до неї, або шукана вершина є недосяжною і шлях до неї відсутній. Ми розглянули саме перший випадок пошуку вершини в графі, коли шукана вершина 7 є досяжною із заданої верши­ни 1. Шлях від вершини 1 до вершини 7 присутній у черзі, але без додаткової інформації він дещо прихований. Для отриман­ня цього шляху необхідно запам’ятовувати також і номери вер­шин, з яких ми побачили кожну наступну вершину. На малюн­ку 28 ця інформація позначена індексами для кожної поточної вершини, записаної у чергу.

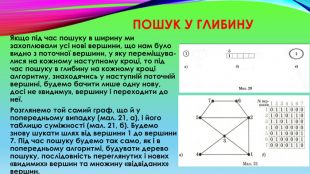
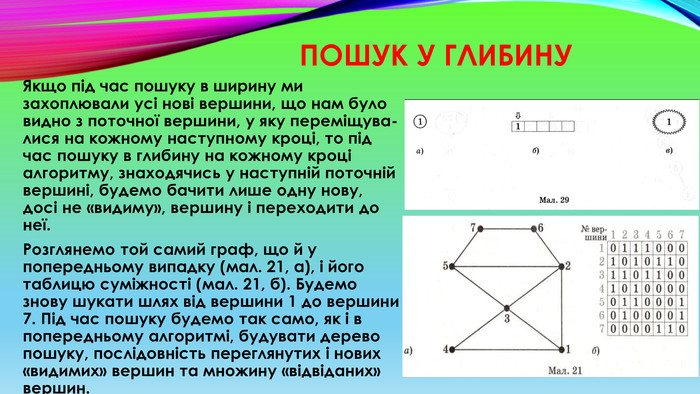
Пошук у глибину. Якщо під час пошуку в ширину ми захоплювали усі нові вер­шини, що нам було видно з поточної вершини, у яку переміщува­лися на кожному наступному кроці, то під час пошуку в глибину на кожному кроці алгоритму, знаходячись у наступній по­точній вершині, будемо бачити лише одну нову, досі не «види­му», вершину і переходити до неї. Розглянемо той самий граф, що й у попередньому випадку (мал. 21, а), і його таблицю суміжності (мал. 21, б). Будемо знову шукати шлях від вершини 1 до вершини 7. Під час по­шуку будемо так само, як і в попередньому алгоритмі, будува­ти дерево пошуку, послідовність переглянутих і нових «види­мих» вершин та множину «відвіданих» вершин.

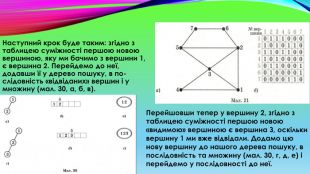
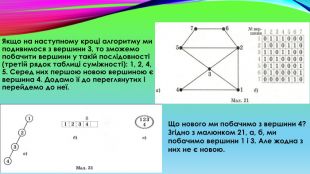
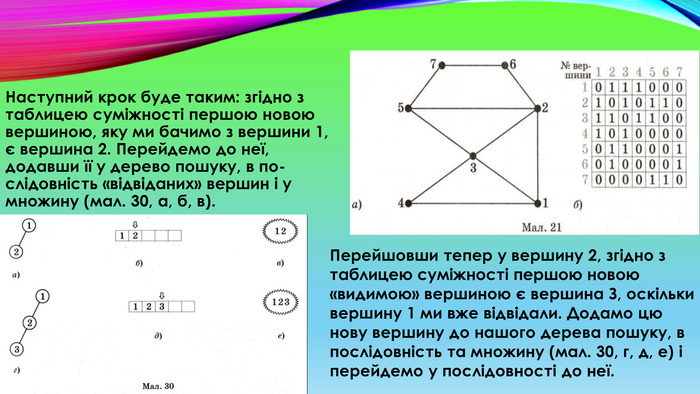
Наступний крок буде таким: згідно з таблицею суміжності першою новою вершиною, яку ми бачимо з вершини 1, є вер­шина 2. Перейдемо до неї, додавши її у дерево пошуку, в по­слідовність «відвіданих» вершин і у множину (мал. 30, а, б, в). Перейшовши тепер у вершину 2, згідно з таблицею суміж­ності першою новою «видимою» вершиною є вершина З, оскільки вершину 1 ми вже відвідали. Додамо цю нову верши­ну до нашого дерева пошуку, в послідовність та множину (мал. 30, г, д, е) і перейдемо у послідовності до неї.

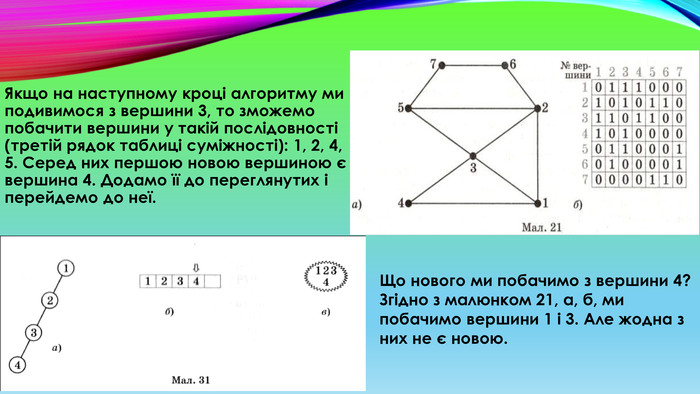
Якщо на наступному кроці алгоритму ми подивимося з вер­шини 3, то зможемо побачити вершини у такій послідовності (третій рядок таблиці суміжності): 1, 2, 4, 5. Серед них першою новою вершиною є вершина 4. Додамо її до переглянутих і пе­рейдемо до неї. Що нового ми побачимо з вершини 4? Згідно з малюн­ком 21, а, б, ми побачимо вершини 1 і 3. Але жодна з них не є новою.

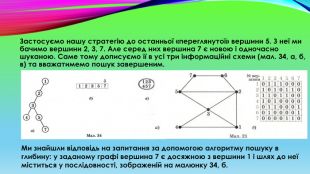
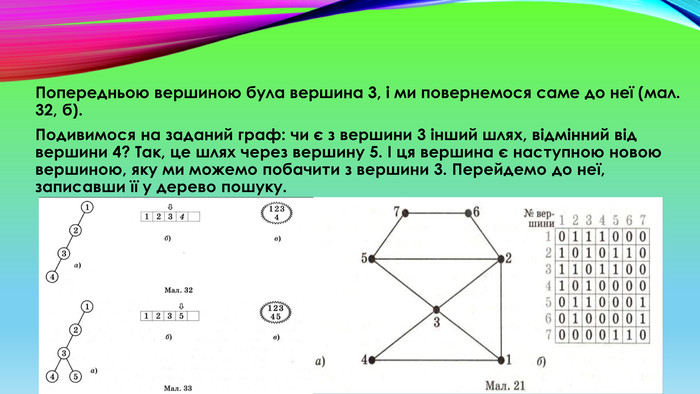
Попередньою вершиною була верши­на 3, і ми повернемося саме до неї (мал. 32, б). Подивимося на заданий граф: чи є з вершини 3 інший шлях, відмінний від вершини 4? Так, це шлях через вершину 5. І ця вершина є наступною новою вершиною, яку ми можемо поба­чити з вершини 3. Перейдемо до неї, записавши її у дерево по­шуку.

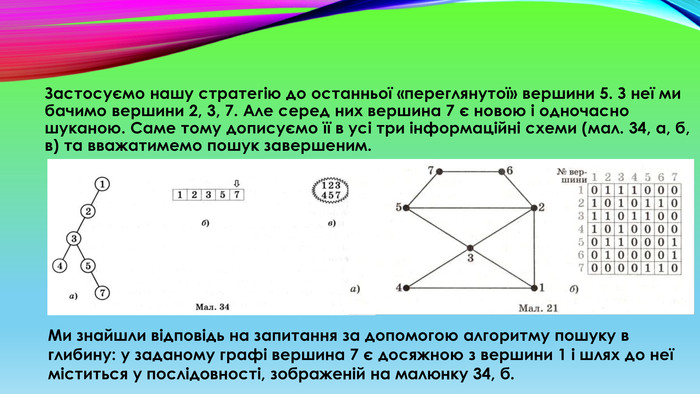
Застосуємо нашу стратегію до останньої «переглянутої» вер­шини 5. З неї ми бачимо вершини 2, 3, 7. Але серед них верши­на 7 є новою і одночасно шуканою. Саме тому дописуємо її в усі три інформаційні схеми (мал. 34, а, б, в) та вважатимемо по­шук завершеним. Ми знайшли відповідь на запитання за допомогою алгорит­му пошуку в глибину: у заданому графі вершина 7 є досяжною з вершини 1 і шлях до неї міститься у послідовності, зобра­женій на малюнку 34, б.

Як видно з покрокового виконання описаного алгоритму, ми весь час працюємо з таблицею суміжності, беручи звідти інфор­мацію про одну нову «видиму» вершину із поточної вершини графа. Ця нова вершина записується у послідовність, яка оброб­ляється за алгоритмом роботи зі стеком: ми дописуємо нову інформацію в кінець цієї послідовності і, у разі потрапляння у тупик, повертаємося до її передостаннього елемента, не роз­глядаючи надалі останній записаний елемент послідовності. І на останок: для запобігання повернення у тупикові вершини інфор­мацію про всі відвідані вершини зберігатимемо у множині. У разі відсут­ності шляху між двома заданими вершинами ми завершимо перегляд усіх записаних у стек вершин, повертаючись кожного разу до попередньої, спорожнивши тим самим стек. Отже, ознакою відсутності шляху в графі між двома заданими верши­нами є те,  що на  деякому кроці алгоритму стек стане порожнім.

алгоритм пошуку в глибину у словесній форміВказати номер вершини k, з якої починається пошук за­даної шуканої вершини l. Почати перегляд вершин заданого графа з вершини k, за­писавши її у стек: і := k. Якщо існує нова вершина з найменшим порядковим но­мером, яку можна побачити з вершини і, то зафіксувати її, за­писавши у стек і збільшивши при цьому індекс вершини сте­ку і на 1: і := і + 1. У протилежному випадку перейти до п. 5. Якщо нова «побачена» вершина, записана у стек, є шука­ною, то перейти до п. 7. Якщо з поточної вершини графа, яка записана у вершині стеку, не видно жодної нової вершини, то відкинути цю верши­ну, перейшовши до попередньої у стеку, зменшивши для цього значення індексу вершини стеку на 1: і := і - 1. Якщо після цьо­го стек став порожнім, тобто і = 0, то перейти до п. 9. Перейти до перегляду наступної «побаченої» вершини і (п. 3). Вивести інформацію про те, що шукану вершину І досяг­нуто і шлях до неї від вершини k існує. Перейти до п. 10. Вивести інформацію про те, що шукана вершина І недо­сяжна від вершини k і шлях до неї відсутній. Завершити алгоритм.

Лабораторна робота № 3 «Пошук у ширину та глибину». Завдання1. Подати дані про графа у вигляді матриці суміжностей. Які це графи?2.   І в. Пошук шляху  у глибину(ширину) по графі з вершини А до Р     ІІ в. Пошук шляху  у глибину(ширину) по графі з вершини 1 до 5