Конспект лекції за відео уроком на тему "Дифракція світла. Дифракційна решітка"

Дифракція світла. Дифракційна решітка

Давайте згадаємо як поводить себе світло, якщо воно падає на широку перешкоду, наприклад щілина між двома лінійками і між ними 1 см відстань(Рис.1).

Малюємо перешкоду довжиною 1 см. На неї падає паралельний  пучок  світла. Якщо описувати з хвильової точки зору паралельний пучок, то це плоска хвиля. У неї є хвильові поверхні, які показані на малюнку. Якщо поставити екран, то промені, які проходять через цю перешкоду, будуть на екрані утворювати чітку ділянку. На малюнку можна побачити – тінь та освітлену область.

Розміри щілини 1 см, а довжина хвилі з вимірювань, які проводилися за часів Юнга Ширина щілина відрізняється на п’ять порядків. Вона у сотні тисяч разів перевищує довжину світлової хвилі. І тому світло поводить себе згідно до законів геометричної оптики.

Проведемо дослід(Рис.2). Візьмемо екран, джерелом світла буду слугувати лазер, він буде його освітлювати. З’являється пляма від лазера на екрані. Беремо дві лінійки і поміщуємо на шляху лазерного променя, відстань між ними 1 см. Ми побачимо геометричну тінь від лінійок. Область освітлена і область геометричної тіні зліва і справа. Все працює згідно до законів геометричної оптики.

А тепер змінимо ситуацію, замість двох лінійок візьмемо щілину 1мм, ширину якої можна регулювати(Рис.3). Помістимо її на шляху лазерного променя і будемо зменшувати ширину щілини. Ми побачимо, що навколо щілини з’являються смужки – вони знаходяться в області геометричної тіні. Якщо звужувати щілину, то відстань між смужками буде більшою. Зрештою і центральна смужка теж збільшиться. Збільшуючи довжину щілини, побачимо, що відстань між смужками зменшується. Якщо щілина достатньо широка, то ми знову спостерігаємо подібно тому, що бачили, коли розташовували на шляху світлового пучка широку сантиметрову щілину. Смуги, схожі на інтерференційну смуги, і це невипадково це дійсно вони. Те що ми спостерігали називається дифракція на щілині.

Можна провести ще один дослід, де можна побачити, що світло не підкорюється законам геометричної оптики(Рис.4). Візьмемо котушку з дротом, мідна дротина діаметром 0,1 мм. Відріжемо трішки від дроту і помістимо на шляху світлового пучка. Ми спостерігаємо, що на шляху тіні – світла пляма, і саме цікаво, що в центрі тіні – світло присутнє. Тобто світло потрапляє в область геометричної тіні  Це підтвердження того, що світло – хвиля.

Схожий експеримент у свій час у 1818 році переконав усіх фізиків, що світло – це хвиля. Історія була такою, що у 1818 році Френель, який є автором однієї із перших теорій дифракції світла, доповідав на засіданні Паризької академії наук свою роботу. Він пояснив чому світло потрапляє в область геометричної тіні, чому при дифракції на щілині

спостерігається, та картина, яку ми вжебачили. В цей час в залі був присутній ще один фізик, прізвище якого Пуассон і послухавши міркування Френеля, він сказав: “Пане Френель, якщо все, що ви кажете правда, то повинно спостерігатися ось таке явище. Якщо на шляху пучка світла помістимо круглу перешкоду і будемо освітлювати точковим джерелом, то в центрі області геометричної тіні, повинна бути біла пляма”.

 Але цього не може бути, якщо світло поводить себе за законами геометричної оптики. Френель подумав і сказав:“Так, повинна бути пляма, потрібно перевірити”. І через деякий час, вони разом та ще з один фізиком на прізвище Араго. Провели такий дослід і переконалися, що в центрі геометричної тіні - яскрава маленька точка. Ця точка отримала назву – пляма Пуассона. Після цього всі фізики були переконані, що світло – хвиля. Враховуючи, що Максвел побудував торію електромагнітних хвиль, що світло – електромагнітна хвиля. І це продовжувалося до початку 20-го століття.

Яким способом можна вивчати дифракцію? Виявляється, що існує два підходи у вивченні дифракції. Перший вид дифракції – дифракція Френеля (Рис.6).

Джерело світла випускає сферичні хвилі. Потім малюємо перешкоду, наприклад круглий отвір і розташовуємо на деякій відстані екран.

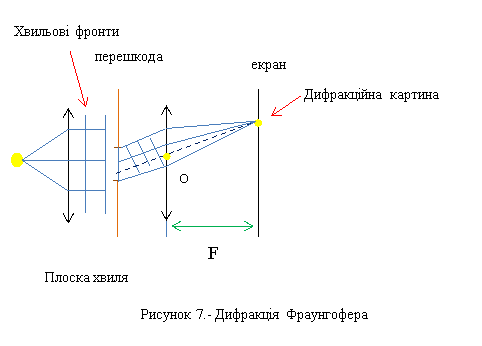
Інший підхід до вивчення дифракції(Рис.7). На перешкоду падає не розбіжний пучок світла, а паралельний. Як можна створити паралельний пучок в лабораторії? Взяти лінзу, в її фокусі помістити точкове джерело світла і лінза буде перетворювати розбіжний пучок в паралельний. Цей паралельний пучок потрапляє на перешкоду, наприклад на щілину або отвір, а потім розташовуємо ще одну лінзу у фокальній площині якої знаходиться екран. F – фокусна відстань лінзи. Що відбувається? На перешкоду падає не сферична хвиля, а плоска. Намалюємо хвильові поверхні або фронти. Далі щось відбувається з хвилями, в результаті взаємодії з отвором. І хвилі, які після проходження, виявляються з правої сторони, можна розглядати як сукупність плоских хвиль, які поширюються в різних напрямках. Візьмемо, наприклад хвилю, яка поширюється в напрямку показаному на малюнку їй відповідає паралельний пучок світла. Через О - оптичний центр лінзи промені пройдуть не заломлюючись і потраплять на екран. Ми розуміємо, що паралельні промені повинні зійтися в одну точку, тобто в побічному фокусі. І ми отримаємо дифракційну картину. Такий вид дифракції називається дифракція Фраунгофера або дифракція плоских хвиль.

Для того, щоб проаналізувати дифракцію, використовується один і той же принцип і у випадку дифракції Френеля, і у випадку дифракції Фраунгофера. Цей принцип називається принцип Гюйгенса – Френеля.

 Принцип Гюйсенса: будь-яка точка простору, якої досягла хвиля, є джерелом вторинних хвиль, що розповсюджуються у всіх напрямках.

Френель запропонував таку методику розрахунку дифракційної картини(Рис.6): там де розташована перешкода, вибрати хвильовий фронт і розбити його на маленькі шматочки. Розглядаємо випромінювання від кожного вторинного  джерела, їх називають зонами Френеля. В точці спостереження ми спостерігаємо інтерференційний максимум або інтерференційний мінімум. Дифракційна картина є результатом інтерференції від всіх вторинних джерел, тобто зон Френеля. В цьому і полягає принцип Гюйгенса – Френеля: хвилі від вторинного джерела інтерферують і дифракційна картина в кожній точці є результатом інтерференції.

Розглянемо один випадок, коли ми можемо розрахувати дифракційну картину в першому приближенні, мова йде про дифракційну решітку. Для того, щоб зробити дифракційну гратку потрібно взяти шматок скла і алмазним різцем (алмаз твердіше скла) нанести на нього багато паралельних штрихів, на строго визначених відстанях один від одного. Ця відстань між штрихами називається періодом дифракційної решітки. Ці штрихи перетворюють скляну пластину в набір великої кількості щілин, через кожну з яких, проходить світлова хвиля. Це так звана прозора дифракційна решітка. Є відбивні гратки, вона відрізняється від прозорої тим, що штрихи наносяться на полірований метал, і виходить дзеркало з великою кількістю таких штрихів. Розглянемо як працює прозора дифракційна решітка(Рис.8). Малюємо дифракційну гратку. Період d дифракційної решітки від верхньої частини однієї щілини до верхньої частини сусідньої щілини. Будемо вважати, що на решітку падає плоска монохроматична хвиля, тобто пучок світла, певної довжини λ. Подивимося, що буде відбуватися. На решітку падає плоска хвиля. Розглянемо дві точки, які відповідають верхньому краю однієї щілини та верхньому краю іншої щілини. Ці точки будемо вважати джерелом вторинних хвиль. Розглянемо хвилі, які розповсюджуються від цих джерел в певному напрямку. Наприклад, під кутом φ. Ми намалювали два промені, які описують одну хвилю, будемо вважати, що випромінювання, яке розповсюджується представляє собою набір плоских хвиль в різних напрямках, виберемо одну з них – це два промені, між якими з’являється різниця ходу Δd. Чому вона рівна? Якщо d – це період дифракційної гратки, а кут під яким аналізуємо випромінювання  φ, його ще називають кут дифракції, то з прямокутного трикутника можна побачити, що гіпотенуза - це d, два кути φ зі взаємно перпендикулярними сторонами, то .                                                                       Виберемо такий напрямок розповсюдження світла, щоб різниця ходу задовольняла умові max, якщо ми змусимо промені інтерферувати, тобто зведемо в одну точку, то ми зможемо спостерігати підсилення цих двох променів, якщо виконується умова max:, тобто різниця ходу дорівнює цілому числу довжин хвиль, де k=0,±1,±2. Як можна звести ці дві точки? За допомогою лінзи. Малюємо лінзу, у фокальній площині паралельні пучки збираються в точку, заломлюючись, крім променя, який проходить через О – оптичний центр лінзи. Якщо виконується умова max: то ці два промені будуть один одного підсилювати. Підставимо (1) в (2): Ми розглянули тільки дві точки, які відповідають двом сусіднім щілинам, але якщо зміщуватися за малюнком вниз, то такі ж дві точки, будуть випромінювати в цьому напрямку, так, що задовольнятимуть умові max. Отже, всі ділянки двох сусідніх щілин будуть випромінювати в цьому напрямку хвилі, які підсилюватимуть один одного, і утвориться інтерференційна картина. Але цього мало, поглянемо на променя, які йдуть не від двох сусідніх щілин, а наприклад від верхівки наступної щілини до верхівки самої нижньої щілини. Чому буде дорівнювати різниця ходу? Оскільки система періодична, то різниця ходу буде задовольняти умові max, якщо Δd подвоїти, то отримаємо умову max, тільки іншого порядку, удвічі більшого. Наступні щілини так само. Але, якщо виконується умова max для сусідніх щілин, то для будь-яких інших в цьому напрямку, буде розповсюджуватися хвиля, окремі промені якої будуть один одного підсилювати, тобто всі щілини породжують інтерференційну картину на екрані, яка виходить дуже яскравою.

Під яким кутом будемо спостерігати max? Під кутом φ. Формула називається формулою дифракційної решітки. На відміну від двох когерентних точкових джерел, дифракційна гратка породжує не картину, де інтенсивність розподілена так(Рис.9): два джерела, max плавно переходить в min. А якщо джерел багато, вони розташовуються в одній площині і когерентні, то виявляється, що max звужуються і різко загострюються, стають дуже високими(Рис.10). Це так звана багатопроменева інтерференція. Ці max тим вище, і тим вужчі, чим більше щілин.

Дифракційні гратки бувають найрізноманітніші від 50 до 2000 . Чим більше , тим менше d. Наприклад, k=1, спостерігаємо max 1-го порядку. Що буде з кутом φ, якщо зменшувати d? Кут φ буде збільшуватися, тобто якщо брати дифракційну решітку все з меншим і меншим періодом, то кут дифракції для тієї самої довжини хвилі буде все більшим і більшим. Але кут дифракції φ, може приймати декілька значень і для кожного k своє. Як же буде виглядати дифракційна картина на малюнку? Намалюємо фрагмент екрану. Коли k=0, φ=0, для будь-якої довжини хвилі на екрані буде max, він називається max нульового порядку. Для цієї довжини хвилі k=1, k=2 і т. д. k може приймати і від’ємні значення, тобто k=-1, k=-2, вони симетричні додатнім k. Спостерігаємо набір інтерференційних max, їх іноді називають дифракційні спектри різних порядків. Якщо направити на дифракційну решітку біле світло? Меншій довжині хвилі відповідає більший кут дифракції, більшій – менший кут. У нас вийде не пляма, а смужки. В центрі буде білий, тому що k=0. 1-ий порядок почнеться з фіолетового , закінчиться червоним. 2-ий порядок буде більш широким і почнеться з фіолетового і далі червоний. Далі будуть спектри більш високого порядкую Будемо пам’ятати, що фіолетові промені відхиляються решіткою менше всього, а червоний більш всього. Давайте подивимося, тепер як це все виглядає в реальності. Візьмемо два лазері один червоний, інший зелений та дифракційну решітку 100 (Рис.11). Направимо випромінювання від цих лазерів на екран.  Спостерігаємо, що відстань між max червоного лазера більше, ніж відстань між max зеленого лазера, тобто довжина хвилі зеленого світла менше, ніж довжина хвилі червоного світла. Візьмемо решітку з більшим числом штрихів 600 та зелений лазер(Рис.12). Побачимо, що до першого порядку відстань велика. Візьмемо відбивну решітку і направимо її не на екран, а проти(Рис.13). Ще можна застосувати лазерний диск, він являє собою велику кількість штрихів, відстань між якими настільки маленька, що ми можемо спостерігати дифракцію на треках(Рис.14). Якщо дивитися на зображення в диску білого світла, то можна побачити райдужне забарвлення, тому що світло з різною довжиною хвилі, дифрагує під різними кутами у відповідності до формули дифракційної решітки.