Конспект уроку на тему "Додавання і відніманя десяткових дробів"
МАТЕМАТИКА, 5 клас
УРОК № ____ Дата ____________
Тема. Множення і ділення десяткових дробів
Мета: підготувати учнів до виконання тематичної контрольної роботи.
Тип уроку: узагальнення і систематизація знань.
Домашнє завдання: ________________________________________
Хід уроку
І. Перевірка домашнього завдання
II. Систематизація знань, умінь і навичок
Запитання до класу
1. Як помножити?
1) Два десяткові дроби;
2) десятковий дріб на 10n;
3) десятковий дріб на 0,1; 0,01;...
2. Скільки цифр треба відділити комою в добутку чисел?
1) 4,25 · 0,3;
2) 42,5 · 0,3;
3) 42,5 · 3;
4) 42,5 · 30.
3. Які властивості множення використовуємо під час обчислення значень виразів?
1) 0,4 · 3,7 · 0,25;
2) 0,4 · 3,7 + 0,4 · 6,3.
4. Як виконати ділення?
1) Десяткового дробу на натуральне число;
2) десяткового дробу на 10n;
3) десяткового дробу на 0,1; 0,01; ....
4) десяткового дробу на десятковий дріб.
Отже, основні правила, яким слід користуватися під час виконання контрольної роботи, — це правила множення і ділення десяткових дробів (використовуючи особливі випадки).
Розв'язування вправ
@ Вправи, які будуть розв'язувати на цьому уроці учні, відповідають основним видам завдань контрольної роботи:
· множення і ділення десяткових дробів;
· усі арифметичні дії з десятковими дробами;
· рівняння і задачі на складання рівнянь.
1. Обчисліть:
1) 0,024 · 4,5;
2) 29,41 · 1000;
3) 2,86 : 100;
4) 4 : 16;
5) 0,48 : 0,8;
6) 9,1 : 0,07.
2. Знайдіть значення виразу (4 – 2,6) · 4,3 + 1,08 : 1,2.
3. Розв'яжіть рівняння:
1) 2,4 (х + 0,98) = 4,08;
2) 0,084 : (6,2 – х) = 32.
4. Відстань між двома пристанями дорівнює 9,9 км. Від цих пристаней в одному напрямку одночасно виїхали два катери. Один катер рухався позаду зі швидкістю 24,6 км/год. і наздогнав другий через 4,5 год. Після початку руху. Знайдіть швидкість другого катера.
Додаткова задача
Петрик купив 5 тістечок і отримав 3,2 грн. здачі. Для покупки 9 тістечок йому не вистачило 2,4 грн. Скільки коштує одне тістечко?
III. Підсумок уроку
Учитель ще раз повторює тематику завдань контрольної роботи.
IV. Рефлексія
Тема. Ділення десяткових дробів на разрядну одиницю.
Мета: доповнити знання учнів правилом ділення десяткових дробів на 0,1; 0,01 і т. д. і закріпити знання загального правила ділення десяткових дробів; відпрацьовувати навички використання названих вище правил під час розв'язування задач, що передбачають виконання ділення десяткових дробів.
Тип уроку: застосування знань, навичок та вмінь.
Домашнє завдання: п. 31 №№ _____________________________________
Хід уроку
I. Перевірка домашнього завдання
2. Після перевірки відповідей і-роз'яснення незрозумілих моментів учні відповідають на запитання вчителя:
- Як поділити десятковий дріб на десятковий дріб?
- Як поділити десятковий дріб на натуральне число?
- Як поділити десятковий дріб на 10; 100; 1000 і т. д.?
- Чому дорівнює частка: 8,4 : 0,2; 0,08 : 0,4; 0,126 : 0,3; 1,2 : 0,06; 8,4 : 10; 1,88 : 100?
II. Вдосконалення знань
Учитель пропонує учням виконати завдання і проаналізувати відповіді.
Завдання. Використавши правило ділення десяткового дробу на десятковий дріб, обчисліть частку:
1) 27,2 : 0,1; 2) 27,2 : 0,01; 3) 27,2 : 0,001.
(Зрозуміло, що 27,2 : 0,1 = 272 : 1 = 272.
27,2 : 0,01 = 2720 : 1 = 2720.
27,2 : 0,001 = 27200 : 1 = 27200.)
Аналіз ситуації, що склалась, можна спростити, запропонувавши запитання:
- Що змінилось у частці стосовно діленого?
- Як ця зміна пов'язана з дільником?
Учні помічають, що при діленні 27,2 на 0,1 кома пересунулась на 1 цифру вправо, на 0,01 — на дві цифри вправо і т. д.)
Висновок. Отже, щоб поділити десятковий дріб на 0,1; 0,01; 0,001, треба перенести кому в діленому на стільки цифр вправо, скільки їх після коми в дільнику.
Приклад: 93,42 : 0,1 = 934,2 або а : 0,1 = а · 10 і т. д.
Тобто тепер ми знаємо, як поводитись при діленні десяткового дробу на:
1) натуральні числа (10n окремо);
2) десяткові дроби (0,1; 0,01; 0,001,... і т. д. окремо).
III. Закріплення знань. Формування вмінь
Розв'язування вправ
№№ _________________________________________________________
@ Коментар. Розв'язуючи перераховані різнопланові завдання, учитель повинен акцентувати роботу учнів на тому, що:
1) треба правильно використовувати вивчені правила й окремі їх випадки під час виконання обчислень;
2) ділення десяткових дробів серед інших арифметичних дій із десятковими дробами виконується майже так, як дії з натуральними числами, тому форма запису і спосіб обчислень майже не зміниться;
3) арифметичні дії з десятковими дробами є лише інструментом для розв'язування інших задач (текстових, рівнянь і т. д.)
IV. Підсумок уроку
Бліц-тест
Виконайте ділення:
|
Варіант 1 |
Варіант 2 |
|
1. 84,6 : 0,1, |
1. 0,73 : 0,01. |
|
1) 846; |
1) 7,3; |
|
2) 8,46; |
2) 73; |
|
3) 84,6; |
3) 0,073; |
|
4) 0,846. |
4) 730. |
|
2. 0,72 : 0,9. |
2. 0,039 : 0,13. |
|
1) 0,8; |
1) 3; |
|
2) 0,08; |
2) 0,3; |
|
3) 8; |
3) 0,26; |
|
4) 0,62. |
4) 30. |
|
3. 89,6 : 28. |
3. 33,28 : 52. |
|
1) 32; |
1) 6,4; |
|
2) 3,2; |
2) 0,64; |
|
3) 0,32; |
3) 0,064; |
|
4) 3,02 |
4) 640 |
Тема. Ділення десяткових дробів
Мета: домогтися засвоєння учнями алгоритму ділення десяткового дробу на натуральне число, встановити алгоритм перетворення звичайного дробу на десятковий; формувати навички розв'язання завдань, що передбачають ділення на натуральне число.
Тип уроку: засвоєння знань, умінь і навичок.
Домашнє завдання п. 32, №№ __________________________________.
Хід уроку
I. Перевірка домашнього завдання і відтворення знань
Після перевірки виконання завдань домашньої роботи учні самостійно виконують завдання аналогічного змісту і такого ж рівня складності (2 учні для перевірки виконують таке ж саме завдання за дошкою).
Самостійна робота
Варіант 1 [2]
1. Виконайте ділення:
1) 8, 61 : 7; 2) 7,68 : 24; 3) 170 : 8. [1) 8,48 : 4; 2) 8,28 : 36; 3) 35 : 14.]
2. Розв'яжіть рівняння: 12 · х = 88,8. [52х = 322,4]
II. Вдосконалення знань
Учитель нагадує учням, що ![]() = а : b, де а і b — натуральні числа, отже, поділивши чисельник а на натуральне b (знаменник), можемо отримати десятковий дріб. Тобто десятковим дробом тепер можемо записати не тільки дроби, що мають вигляд
= а : b, де а і b — натуральні числа, отже, поділивши чисельник а на натуральне b (знаменник), можемо отримати десятковий дріб. Тобто десятковим дробом тепер можемо записати не тільки дроби, що мають вигляд ![]() , а й деякі інші дроби (де b — не є розрядною одиницею): для цього треба лише поділити чисельник дробу на його знаменник.
, а й деякі інші дроби (де b — не є розрядною одиницею): для цього треба лише поділити чисельник дробу на його знаменник.
|
Приклад (№ 936). |
|
Завдання 1. Перетворити на десятковий дріб і запам'ятати:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
(![]() = 0,5;
= 0,5; ![]() = 0,25;
= 0,25; ![]() = 0,2;
= 0,2; ![]() = 0,4;
= 0,4; ![]() = 0,6;
= 0,6; ![]() = 0,8;
= 0,8; ![]() = 0,125.)
= 0,125.)
III. Відпрацювання навичок
Розв'язання вправ
@ На цьому уроці учні закріплюють знання алгоритму ділення на натуральне число і перетворення звичайного дробу на десятковий. Тому розв'язують задачі, що передбачають виконання цих дій: №№ ______(парні): ________; також № ______, що передбачає сумісне виконання арифметичних дій з десятковими дробами і № __________(повторення геометричного матеріалу).
IV. Підсумок уроку
Запитання до класу
1. Поясніть, як виконати ділення:
1) 2,7 : 3; 2) 5 : 2; 3) 184 : 10.
2. Поясніть, як записати десятковим дріб ![]() .
.
Тема. Множення десяткових дробів
Мета: вдосконалити знання учнів правилом множення десяткового дробу на 0,1; 0,01 і т. д.; закріпити знання правил множення десяткового дробу на 10n, на десятковий дріб і на 0,1; 0,01 і т. д. і ділення десяткового дробу на 10п; формувати вміння застосовувати ці правила для розв'язування завдань, що передбачає, крім усіх відомих раніше, застосування цих правил.
Тип уроку: засвоєння навичок та вмінь.
Домашнє завдання: п. 31, №№ ______________________________________.
Хід уроку
І. Перевірка домашнього завдання
Бажано ретельно перевірити виконання домашніх вправ на предмет засвоєння правил, розглянутих на попередньому уроці. Тому вчитель заздалегідь за відкритою дошкою записує відповіді до вправ домашньої роботи, і учні перевіряють або кожний свою роботу, або, за умови налагодженої парної форми роботи, зошити сусіда. Можна запропонувати учням самостійно виконати завдання:
Варіант 1 [2]
1. Виконайте дії: 1) 2,53 · 10; 2) 2,53 · 100; 3) 2,53 · 1000.
[1) 1,78 · 10; 2) 1,78 · 100; 3) 1,78 · 1000.]
2. Виконайте дії: 1) 56,79 : 10; 2) 56,79 : 100; 3) 56,79 : 1000.
[1) 27,41 : 10; 2) 27,41 : 100; 3) 17,41 : 1000.]
3. Знайдіть добуток: 1) 0,3 і 1,7; 2) 3 і 1,7; 3) 1,5 і 0,18.
[1) 2,3 і 0,8; 2) 8 і 2,3; 3) 2,4 і 0,15.]
II. Застосування знань
Учитель пропонує учням такі завдання:
1) Використовуючи правило множення десяткових дробів, знайдіть добуток:
4,6 і 0,1; 4,6 і 0,01; 4,6 і 0,001.
(4,6 · 0,1 = 0,46; 4,6 · 0,01 = 0,046; 4,6 · 0,001 = 0,0046)
2) Використовуючи результат попереднього завдання, з'ясуйте, як змінилось місце коми в числі 4,6 при множенні цього дробу на 0,1; 0,01; 0,001? Зробіть висновок.
Висновок. Щоб помножити десятковий дріб на 0,1; 0,01; 0,001 і т. д., достатньо в цьому дробі перенести кому вліво відповідно на 1, 2, 3 і т. д. цифр.
На закріплення цього учням можна запропонувати вправу:
Знайдіть пропущені числа:
1) 35,1 · □ = 0,351;
2) 436 · □ = 0,436;
3) 6,58 · □ = 0,658;
4) 65,8 · □ = 6,58.
@ Після розгляду особливого випадку множення десяткових дробів учитель робить зауваження: тепер відомо, як виконувати завдання на множення двох чисел із участю десяткових дробів. Але часто, розв'язуючи задачі, треба виконувати множення разом із додаванням і відніманням. Зрозуміло, що в цьому випадку можна використовувати звичайний порядок дій: спочатку виконуємо дії в дужках, потім множення і ділення (по порядку зліва направо), потім додавання і віднімання (по порядку зліва направо). Окремо можна згадати піднесення десяткового дробу до степеня.
IІІ. Засвоєння знань, формування вмінь
Розв'язування вправ
1. Множення десяткового дробу на 0,1; 0,01; 0,001 і т. д.: №№ __________.
2. Множення двох десяткових дробів: № _______________.
3. Вирази на сумісні дії додавання, віднімання, множення десяткових дробів: №№ ____________________.
4. Задачі на виконання додавання, віднімання і множення десяткових дробів №№ ______________________.
МАТЕМАТИКА, 5 клас
УРОК № ____ Дата ____________
Тема. Множення десяткових дробів.
Мета: ввести поняття множення десяткових дробів та сформулювати загальне правило множення десяткових дробів; розпочати роботу з формування вмінь застосовувати правило множення десяткових дробів.
Тип уроку: засвоєння нових знань.
Домашнє завдання п. 31, №№ ____________________________________
Хід уроку
I. Актуалізація опорних знань
Запитання до класу
1. Як записати суму однакових доданків, кожний з яких дорівнює а, якщо кількість таких доданків у сумі дорівнює:
1) 2; 2) 5; 3) 10; 4) b.
2. Як зміниться добуток ab, якщо:
1) а збільшити в 2 рази, а b збільшити в 3 рази;
2) а збільшити в 2 рази, а b зменшити в 2 рази;
3) а збільшити в 10 разів, а b зменшити у 100 разів?
3. Як знайти число, яке менше від даного числа о у:
1) у 10 разів; 2) у 100 разів; 3) у 10n разів?
II. Мотивація навчальної діяльності
У ч и т е л ь. Ви вже знаєте і вмієте виконувати додавання і віднімання десяткових дробів і розв'язувати задачі на застосування цих дробів. Але чи знаєте, що існують ще дві арифметичні дії: множення і ділення, за допомогою яких також можна розв'язувати багато задач. Наприклад, як знайти площу прямокутника, якщо довжини його сторін дорівнюють 2,3 м і 1,5 м? Як знайти відстань, яку проїхав велосипедист за 2,5 год. зі швидкістю 18,5 км/год.? Ці і багато інших задач треба розв'язувати, виконавши дію множення десяткових дробів (2,3 · 1,5 і 18,5 · 2,5). Тому сьогодні ми розпочинаємо вивчення нової теми «Множення натуральних чисел», в ході якого дізнаємось, як виконується множення десяткових дробів, десяткового дробу на розрядні одиниці та які властивості притаманні множенню десяткових дробів.
III. Формування знань
@ Оскільки висвітлення цієї теми в підручнику не є традиційним, а система задач теми відповідає саме цій нетрадиційній темі вивчення множення десяткових дробів, викладання нового матеріалу найкраще подати близько за підручником (або організовувати роботу класу з підручником) і на цьому уроці треба висвітлити такі питання:
1. Як записати у вигляді суми добуток: а ·10, а · 100?
2. Як знайти, записавши у вигляді суми значення виразів: 0,2 · 10; 36 · 10; 5,2 · 10; 0,27 · 10?
3. Як знайти значення виразів 0,2 · 10; 1,36 · 10; 5,2 · 10; 0,27 · 10 без запису добутку у вигляді суми?
4. Як помножити десятковий дріб на 10; 100; 1000 і 10n?
5. Як поділити десятковий дріб на 10; 100; 1000 і 10n?
6. Як перемножити два десяткових дроби, використовуючи правила множення і ділення на 10п ?
7. Як знайти добуток двох десяткових дробів, використовуючи множення натуральних чисел?
IV. Закріплення знань, засвоєння вмінь
На цьому уроці (першому в темі) учні розв'язують завдання початкового і середнього рівня, і основну увагу треба приділити засвоєнню правил множення і ділення на 10п та загального правила множення двох десяткових дробів.
Розв'язання вправ
№№ 876 (усно); 877; 878; 880; 882, 883 (1; 3; 5; 7); 890; 891.
@ Розв'язуючи вправи, треба звернути увагу учнів на випадки, коли:
1) кому треба перенести на таку кількість цифр, яка перевищує кількості цифр у дробовій частині (при множенні) і цілій частині (при діленні);
2) при множенні десяткових дробів — остання цифра дробової частини — нуль;
3) один з множників — натуральне число (кількість цифр у дробовій частині такого числа дорівнює 0).
V. Підсумок уроку
Контрольні запитання
1. Як помножити десятковий дріб на 10n?
2. Як поділити десятковий дріб на 10n?
3. Розкажіть, як виконати множення 4,2 на 8,14?
МАТЕМАТИКА, 5 клас
УРОК № ____ Дата ____________
Тема. Поняття про десятковий дріб. Порівняння, округлення,
додавання і віднімання десяткових дробів
Мета: перевірити рівень навчальних досягнень учнів з теми.
Тип уроку: перевірка й корекція знань, навичок і вмінь.
Хід уроку
І. Умова тематичної контрольної роботи
Варіант 1
1°. Порівняйте: 1) 18, 3 і 18,287; 2) 0,5438 і 0,544.
2°. Округліть 1) до десятих: 3,875; 0,4351; 2) до сотих: 11,232; 0,4759.
3°. Виконайте дії:
1) 7,76 + 43,693; 2) 77,16 – 7,243; 3) 11 – 5,625; 4) 10,5 – (0,88 + 3,286).
4°. Швидкість пароплава проти течії річки дорівнює 24,8 км/год., а швидкість течії 2,7 км/год. Знайдіть швидкість пароплава за течією.
5*. Запишіть у метрах і обчисліть: 1) 32,5 м - 92 см; 2) 4, 3 км + 740 м.
6*. Ламана складається з трьох ланок. Довжина першої ланки дорівнює 8,3 см, що на 3,8 см менше від довжини другої ланки і на 2,7 см більше за довжину третьої. Чому дорівнює довжина ламаної?
7*. Напишіть чотири числа, кожне з яких більше за 7,33 і менше від 7,36.
8**. Які цифри можна поставити замість зірочок, щоб утворилася правильна нерівність (у правій і лівій частинах нерівності зірочкою позначено одну й ту саму цифру): 1) 0,*4 > 0,6 *; 2) 0,*5 < 0,5 *?
Варіант 2
1°. Порівняйте: 1) 21,397 і 21,4; 2) 0,825 і 0,8248.
2°. Округліть: 1) до десятих: 8,347; 0,86945; 2) до сотих: 13,9261; 0,4677.
3°. Виконайте дії:
1) 5,98 + 42,467; 2) 46,45 – 6,815; 3) 39 – 5,973; 4) 43,7 – (7,64 + 0,983).
4°. Швидкість катера за течією річки дорівнює 28,2 км/год., а власна швидкість катера 25,5 км/год. Знайдіть швидкість катера проти течії.
5*. Запишіть у метрах і обчисліть: 1) 19, 3 м - 58 см; 2) 3,6 км + 450 м.
6*. Одна зі сторін трикутника дорівнює 8,2 см, що на 3,9 см менше від довжини другої сторони і на 2,3 см більше за довжину третьої сторони трикутника. Знайдіть периметр трикутника.
7*. Напишіть чотири числа, кожне з яких менше від 3,72 і більше за 3,75.
8**. Які цифри можна поставити замість зірочок, щоб утворилася правильна нерівність (у правій і лівій частинах нерівності зірочкою позначено одну й ту саму цифру): 1) 0,*3 > 0,6 *; 2) 0,*4 < 0,4*?
II. Розв'язання і відповіді
Варіант 1
1°. 1) 18,300 > 18,287; 2) 0,5438 < 0,5440.
2°. 1) 3,875 ![]() 3,9; 0,4351
3,9; 0,4351 ![]() 0,4; 2) 11,232
0,4; 2) 11,232 ![]() 11,23; 0,4759
11,23; 0,4759 ![]() 0,48.
0,48.
3°. 1) 51,453; 2) 69,917; 3) 5,375; 4) 6,334.
4°. 1) 24,8 + 2,7 = 27,5 (км/год.) — власна швидкість;
2) 27,5 + 2,7 = 30,2 (км/год.) — швидкість за течією.
Відповідь. 30,2 км/год.
5*. 1) 32,5 м – 92 см = 32,5 м – 0,92 м = 31,58 м.
2) 4,3 км + 740 м = 4300 м + 740 м = 5040 м.
6*. 8,3 + (8,3 + 3,8) + (8,3 – 2,7) = 26 (см) - довжина ламаної.
7*. 7,330 < х < 7,360; х може набувати одного із значень: 7,331; 7,332; 7,342; 7,359.
8**. 1) * Може набувати значень: 7, 8, 9;
2) * може набувати значень: 4, 3, 2, 1, 0.
Варіант 2
1°. 1) 21,397 < 21,400, 2) 0,8250> 0,8248.
2°. 1) 8,347 ![]() 8,3; 0,86945
8,3; 0,86945 ![]() 0,9; 2)13,9261
0,9; 2)13,9261 ![]() 13,93; 0,4677
13,93; 0,4677 ![]() 0,48.
0,48.
3°. 1) 48,447; 2) 39,635; 3) 33,027; 4) 35,077.
4°. 1) 28,2 – 25,5 = 2,7 (км/год.) — швидкість течії;
2) 25,5 – 2,7 = 22,8 (км/год.) — швидкість проти течії.
Відповідь. 22,8 км/год.
5*. 1) 19,3 м – 58 см = 19, 3 м – 0,58 м = 18,72м;
2) 3,6 км + 450 м = 3600 м + 450 м = 4050 м.
6*. 1) 8,2 + (8,2 + 3,9) + (8,2 – 2,3) = 26,2 (см) - периметр трикутника.
Відповідь. 26,2 см.
7*. 3,720 < х < 3,750; х може набувати також значень: 3,721; 3,733; 3,747; 3,749.
8**. 1) * може набувати таких значень: 7, 8,9;
2) * може набувати таких значень: 3, 2,1, 0.
Варіант 1
1°. Порівняйте: 1) 18, 3 і 18,287; 2) 0,5438 і 0,544.
2°. Округліть 1) до десятих: 3,875; 0,4351; 2) до сотих: 11,232; 0,4759.
3°. Виконайте дії:
1) 7,76 + 43,693; 2) 77,16 – 7,243;
3) 11 – 5,625; 4) 10,5 – (0,88 + 3,286).
4°. Швидкість пароплава проти течії річки дорівнює 24,8 км/год., а швидкість течії 2,7 км/год. Знайдіть швидкість пароплава за течією.
5. Запишіть у метрах і обчисліть: 1) 32,5 м - 92 см; 2) 4, 3 км + 740 м.
6*. Ламана складається з трьох ланок. Довжина першої ланки дорівнює 8,3 см, що на 3,8 см менше від довжини другої ланки і на 2,7 см більше за довжину третьої. Чому дорівнює довжина ламаної?
7*. Напишіть чотири числа, кожне з яких більше за 7,33 і менше від 7,36.
8**. Які цифри можна поставити замість зірочок, щоб утворилася правильна нерівність (у правій і лівій частинах нерівності зірочкою позначено одну й ту саму цифру): 1) 0,*4 > 0,6 *; 2) 0,*5 < 0,5 *?
Варіант 2
1°. Порівняйте: 1) 21,397 і 21,4; 2) 0,825 і 0,8248.
2°. Округліть: 1) до десятих: 8,347; 0,86945; 2) до сотих: 13,9261; 0,4677.
3°. Виконайте дії:
1) 5,98 + 42,467; 2) 46,45 – 6,815;
3) 39 – 5,973; 4) 43,7 – (7,64 + 0,983).
4°. Швидкість катера за течією річки дорівнює 28,2 км/год., а власна швидкість катера 25,5 км/год. Знайдіть швидкість катера проти течії.
5. Запишіть у метрах і обчисліть: 1) 19, 3 м - 58 см; 2) 3,6 км + 450 м.
6*. Одна зі сторін трикутника дорівнює 8,2 см, що на 3,9 см менше від довжини другої сторони і на 2,3 см більше за довжину третьої сторони трикутника. Знайдіть периметр трикутника.
7*. Напишіть чотири числа, кожне з яких менше від 3,72 і більше за 3,75.
8**. Які цифри можна поставити замість зірочок, щоб утворилася правильна нерівність (у правій і лівій частинах нерівності зірочкою позначено одну й ту саму цифру): 1) 0,*3 > 0,6 *; 2) 0,*4 < 0,4*?
МАТЕМАТИКА, 5 клас
УРОК № ____ Дата ____________
Тема. Додавання і віднімання десяткових дробів. Самостійна робота.
Мета: узагальнити досвід учнів, набутий під час вивчення теми «Додавання і віднімання десяткових дробів»; перевірити ступінь засвоєння знань, умінь учнів з теми.
Тип уроку: перевірка та корекція знань, навичок та вмінь
Домашнє завдання п. 28 - 30, № № _______________________________
Хід уроку
І. Відтворення знань
Усні вправи
1. Знайдіть числа, яких не вистачає в ланцюжку обчислень:
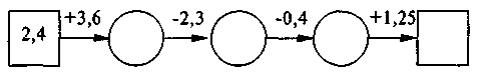
2. Власна швидкість моторного човна дорівнює 11,2 км/год., а швидкість течії річки — 2,3 км/год. Знайдіть швидкість човна за течією і його швидкість проти течії.
3. Як зміниться сума, якщо:
1) один додаток збільшити на 2,8, а другий — зменшити на 2,8;
2) кожний додаток збільшити на 2,8;
3) один додаток збільшити на 4, а другий — зменшити на 3,5?
4. Обчисліть периметр рівнобедреного трикутника, одна із сторін якого 4,8 см, а друга 3, 2 см.
II. Розв'язування задач
1. Знаходження значення виразу: № _____________.
2. Розв'язування рівнянь: № _____________.
3. Вираження величин: 1) 5,2 м – 3 см; 2) 5,2 м – 3 дм;
3) 5,2 км – 3 м.
Додаткові задачі
1. Обчисліть, записавши дані величини в дециметрах:
1) 6,29 дм – 14 см; 2) 3,2 дм + 8 см;
3) 28 дм – 146 см; 4) 4 м 6 дм 5 см – 27 см 4 мм.
4. За перший день туристи пройшли 5,4 км, що на 1,7 км більше, ніж за другий день, і на 2,1 км менше, ніж за третій. Скільки кілометрів пройшли туристи за три дні?
5. Заповніть таблицю:
|
Власна швидкість катера |
Швидкість течії річки |
Швидкість катера за течією |
Швидкість катера проти течії |
|
13 км/год. |
2,5 км/год. |
|
|
|
19 км/год. |
|
22,1 км/год. |
|
|
24 км/год. |
|
|
21 км/год. |
|
|
2 км/год. |
18,5 км/год. |
|
|
|
2,5 км/год. |
|
17 км/год. |
III. Контроль засвоєння знань
Варіант 1
1. Яким з перелічених виразів задається (у т) сума: 2т 28 кг, 1 т 5 кг, 5 т 4 ц?
1) 8,568 т; 2) 8,73 т; 3) 8,433 т; 4) 8,326 т.
2. Знайдіть рівняння, коренем якого є число 10:
1) х – 2,093 = 0,207; 2) 2,093 – х = 0,207;
3) 12,093 – х = 2,093; 4) х + 2,093 = 12,93.
3. Яке з наведених чисел дорівнює різниці 10 – 0,090908?
1) 9,010101; 2) 9,909092; 3) 9,090902; 4) 0,919192.
4. Яке з поданих чисел дорівнює сумі коренів рівнянь х – 1,048 = 0,909 і 1,005 – х = 0,044, округлений до сотих? 1) 2,92; 2) 1,19; 3) 1,2; 4) 2,91.
5. Яка з пар чисел є значенням власної швидкості катера проти течії, якщо швидкість течії річки 2,3 км/год., а швидкість за течією 18,1 км/год?
1) 16,2 і 13,9; 2) 15,8 і 13,5; 3) 20,4 і 18,1; 4) 20,4 і 22,7.
Варіант 2
1. Який з поданих виразів дорівнює вираженій у метрах сумі: 7 м 5 дм, 3 м 7 см і 2 м 88 мм?
1) 12,955 м; 2) 12,658 м; 3) 12,838 м; 4) 14,08 м.
2. Коренем якого з наведених рівнянь є число 2,005?
1) х + 1,195 = 3,2 2) 3,2 – х = 0,195;
3) 2,005 – х = 0; 4) 1,005 + х = 2,005.
3. Яке з поданих чисел дорівнює різниці 4 – 2,9996?
1) 2,9994; 2) 2,0004; 3) 1,9994; 4) 1,0004.
4. Яке з названих чисел є сумою коренів рівнянь х + 5,4 = 10,3 і х – 3,8 = 8,9 з точністю до одиниць? 1) 17; 2) 18; 3) 17,6; 4) 16.
5. Яка з наведених пар чисел є записом значень власної швидкості катера і швидкості за течією, якщо швидкість течії річки 2,6 км/год., а швидкість проти течії 17,2 км/год.?
1) 14,6 і 12; 2) 19,8 і 22,4; 3) 19,8 і 14,6; 4) 19,8 і 17,2.
Коди відповідей:
|
|
1 |
2 |
3 |
4 |
5 |
|
В. 1 |
3 |
3 |
2 |
1 |
2 |
|
В. 2 |
2 |
3 |
4 |
2 |
2 |
Заповніть таблицю:
|
Власна швидкість катера |
Швидкість течії річки |
Швидкість катера за течією |
Швидкість катера проти течії |
|
13 км/год. |
2,5 км/год. |
|
|
|
19 км/год. |
|
22,1 км/год. |
|
|
24 км/год. |
|
|
21 км/год. |
|
|
2 км/год. |
18,5 км/год. |
|
|
|
2,5 км/год. |
|
17 км/год. |
Заповніть таблицю:
|
Власна швидкість катера |
Швидкість течії річки |
Швидкість катера за течією |
Швидкість катера проти течії |
|
13 км/год. |
2,5 км/год. |
|
|
|
19 км/год. |
|
22,1 км/год. |
|
|
24 км/год. |
|
|
21 км/год. |
|
|
2 км/год. |
18,5 км/год. |
|
|
|
2,5 км/год. |
|
17 км/год. |
Заповніть таблицю:
|
Власна швидкість катера |
Швидкість течії річки |
Швидкість катера за течією |
Швидкість катера проти течії |
|
13 км/год. |
2,5 км/год. |
|
|
|
19 км/год. |
|
22,1 км/год. |
|
|
24 км/год. |
|
|
21 км/год. |
|
|
2 км/год. |
18,5 км/год. |
|
|
|
2,5 км/год. |
|
17 км/год. |
Варіант 2
1. Який з поданих виразів дорівнює вираженій у метрах сумі: 7 м 5 дм, 3 м 7 см і 2 м 88 мм?
1) 12,955 м; 2) 12,658 м; 3) 12,838 м; 4) 14,08 м.
2. Коренем якого з наведених рівнянь є число 2,005?
1) х + 1,195 = 3,2 2) 3,2 – х = 0,195;
3) 2,005 – х = 0; 4) 1,005 + х = 2,005.
3. Яке з поданих чисел дорівнює різниці 4 – 2,9996?
1) 2,9994; 2) 2,0004; 3) 1,9994; 4) 1,0004.
4. Яке з названих чисел є сумою коренів рівнянь х + 5,4 = 10,3 і х – 3,8 = 8,9 з точністю до одиниць? 1) 17; 2) 18; 3) 17,6; 4) 16.
5. Яка з наведених пар чисел є записом значень власної швидкості катера і швидкості за течією, якщо швидкість течії річки 2,6 км/год., а швидкість проти течії 17,2 км/год.? 1) 14,6 і 12; 2) 19,8 і 22,4; 3) 19,8 і 14,6; 4) 19,8 і 17,2.
Варіант 1
1. Яким з перелічених виразів задається (у т) сума: 2т 28 кг, 1 т 5 кг, 5 т 4 ц?
1) 8,568 т; 2) 8,73 т; 3) 8,433 т; 4) 8,326 т.
2. Знайдіть рівняння, коренем якого є число 10:
1) х – 2,093 = 0,207; 2) 2,093 – х = 0,207;
3) 12,093 – х = 2,093; 4) х + 2,093 = 12,93.
3. Яке з наведених чисел дорівнює різниці 10 – 0,090908?
1) 9,010101; 2) 9,909092; 3) 9,090902; 4) 0,919192.
4. Яке з поданих чисел дорівнює сумі коренів рівнянь х – 1,048 = 0,909 і
1,005 – х = 0,044, округлений до сотих? 1) 2,92; 2) 1,19; 3) 1,2; 4) 2,91.
5. Яка з пар чисел є значенням власної швидкості катера проти течії, якщо швидкість течії річки 2,3 км/год., а швидкість за течією 18,1 км/год?
1) 16,2 і 13,9; 2) 15,8 і 13,5; 3) 20,4 і 18,1; 4) 20,4 і 22,7.
Варіант 2
1. Який з поданих виразів дорівнює вираженій у метрах сумі: 7 м 5 дм, 3 м 7 см і 2 м 88 мм?
1) 12,955 м; 2) 12,658 м; 3) 12,838 м; 4) 14,08 м.
2. Коренем якого з наведених рівнянь є число 2,005?
1) х + 1,195 = 3,2 2) 3,2 – х = 0,195;
3) 2,005 – х = 0; 4) 1,005 + х = 2,005.
3. Яке з поданих чисел дорівнює різниці 4 – 2,9996?
1) 2,9994; 2) 2,0004; 3) 1,9994; 4) 1,0004.
4. Яке з названих чисел є сумою коренів рівнянь х + 5,4 = 10,3 і х – 3,8 = 8,9 з точністю до одиниць? 1) 17; 2) 18; 3) 17,6; 4) 16.
5. Яка з наведених пар чисел є записом значень власної швидкості катера і швидкості за течією, якщо швидкість течії річки 2,6 км/год., а швидкість проти течії 17,2 км/год.?
1) 14,6 і 12; 2) 19,8 і 22,4; 3) 19,8 і 14,6; 4) 19,8 і 17,2.
МАТЕМАТИКА, 5 клас
УРОК № ____ Дата ____________
Тема. Додавання і віднімання десяткових дробів.
Мета: встановити загальні правила додавання і віднімання десяткових дробів; формувати вміння застосовувати ці знання на практиці (у розв'язуванні задач початкового і середнього рівня).
Тип уроку: засвоєння нових знань.
Домашнє завдання: п.______, №№ _________________________________
Хід уроку
I. Актуалізація опорних знань
Усні вправи
1. Записати у вигляді звичайного дробу: 0,3; 0,32; 0,03; 1,725; 2,374.
2. Виконати дії: 1) 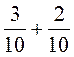 ; 2)
; 2) 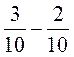 ; 3)
; 3) 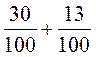 ; 4)
; 4) 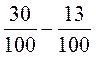 ; 5)
; 5) 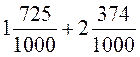 ; 6)
; 6) 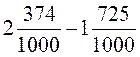 .
.
3. Записати всі числа з однаковою кількістю цифр у дробових частинах: 1,2; 0,03; 13,170.
4. Обчислити: 1) 7 + 15; 2) 70 + 15; 3) 7 + 150; 4) 70 + 150; 5) 15 – 7; 6) 150 – 7; 7) 70 – 15; 8) 150 – 70.
5. Розв'язати рівняння: 1) 27 + х = 35; 2) 35 – х = 27; 3) х – 27 = 35.
II. Засвоєння знань
@ Засвоєння теми «Додавання і віднімання десяткових дробів» в цілому не викликає в учнів труднощів (розглянувши приклад, поданий у підручнику із застосуванням переходу до звичайних дробів із однаковими знаменниками, більшість учнів самостійно «відкриває» правила додавання, а від нього й віднімання десяткових дробів). Тому основне завдання вчителя в цій ситуації — акцентувати увагу учнів на перевагу запису дробів у вигляді десяткових саме в плані виконання арифметичних дій (у цьому випадку додавання і віднімання). Учні повинні засвоїти, що додавання і віднімання десяткових дробів виконується в стовпчик майже так само, як додавання і віднімання натуральних чисел. Єдине, що відрізняє ці два випадки, то коли виконується додавання (віднімання) натуральних чисел, ми просто записуємо останню цифру під останньою; коли ж виконуємо додавання і віднімання десяткових дробів — перед виконанням дій і записом чисел «у стовпчик» ми повинні «підготувати» числа до цього — зрівняти кількість цифр після коми.
Додавання і віднімання десяткових дробів
Додавайте (віднімайте) десяткові дроби як натуральні числа — порозрядно!
Зберігайте місце коми:
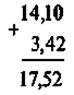
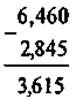
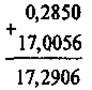
IV. Засвоєння умінь та навичок
На цьому уроці учні розв'язують завдання початкового і середнього рівня складності, бо головне для учнів — засвоїти і навчитись використовувати алгоритм:
1) Зрівняй кількість цифр після коми в обох числах.
2) Запиши у стовпчик, щоб кома знаходилась під комою; додавай (віднімай) як натуральні числа.
3) Постав кому в сумі (різниці) під комою в даних числах (збережи місце коми).
За цією схемою учні розв'язують вправи: №№_____________________________________________________________
Додаткові вправи: _______________________
IV. Підсумок уроку
Учитель ще раз наголошує, що виконання додавання і віднімання десяткових дробів мало відрізняється від правила додавання і віднімання натуральних чисел — і це очевидна перевага такої форми запису дробів.
МАТЕМАТИКА, 5 клас
УРОК № ____ Дата ____________
Тема. Десятковий дріб. Запис десяткових дробів.
Мета: формувати поняття про десятковий дріб; уміння записувати й читати десяткові дроби, спираючись на знання розрядів десяткового дробу.
Тип уроку: засвоєння знань і вмінь.
Домашнє завдання ______________________________________________
Хід уроку
І. Актуалізація опорних знань
Усні вправи
1. Знайти значення степеня: 101, 102, 103, 104,10n, якщо n — натуральне число. 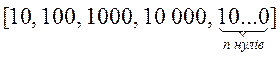
2. 1) Яку частину метра становить 1 см, 3 дм, 4 мм?
2) Яку частину тонни становить 1 кг, 5 ц, 346 кг?
3) Яку частину квадратного метра становить: 1 дм2, 8 см2?
[1)1 см = ![]() м, 3 дм =
м, 3 дм = ![]() м, 4мм =
м, 4мм = 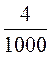 м;
м;
2) 1 см = 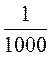 м, 5 ц =
м, 5 ц = ![]() т, 346 кг =
т, 346 кг = 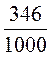 г;
г;
3) 1 дм2 = ![]() м2, 8см2 =
м2, 8см2 = 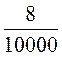 м2.]
м2.]
II. Формування знань
@ Оскільки в 5 класі поняття десяткового дробу розглядається після поняття звичайного дробу, формування уявлення про десятковий дріб базується на уявленні про звичайні дроби, а саме десятковий дріб розглядається як «скорочена» форма запису звичайного дробу, тобто запис, в якому знаменник відсутній і знаменником якого є степінь числа 10. (Тому відразу слід звернути увагу на два моменти:
1) Десятковим дробом можна записати як правильні дроби (![]() = 0,3;
= 0,3; ![]() = 0,07), — тоді в цілій частині ми маємо 0 (нуль цілих), так і неправильні дроби, (попередньо виділивши в них цілу частину, і мішані числа (
= 0,07), — тоді в цілій частині ми маємо 0 (нуль цілих), так і неправильні дроби, (попередньо виділивши в них цілу частину, і мішані числа (![]() = 4
= 4![]() = 4,3).
= 4,3).
2) Під час запису звичайного правильного дробу десятковим необхідно одразу перевірити, чи співпадає кількість цифр чисельника із кількістю нулів знаменника (якщо ні — дописати необхідну кількість нулів перед чисельником у дробовій частині).
При цьому учні часто не розуміють, що означає «приписати нуль перед чисельником у дробовій частині десяткового дробу.
Тому для попередження такого моменту можна запропонувати учням завдання:
1) Запишіть число 17. Допишіть два нулі перед числом 17; нуль після числа 17.
2) У запису 0,17 назвіть цілу та дробову частину. Допишіть один нуль (два нулі) перед числом 17 у дробовій частині.
3) Запишіть у вигляді десяткового дробу: ![]() ;
; 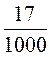 ;
; 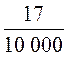 ;
; 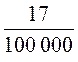 .
.
4) Прочитайте десяткові дроби: 1,6; 12,8; 5,24; 6,325; 0,5; 0,05; 0,005. Друга частина теми присвячена питанню розрядів десяткових дробів.
Важливість цього питання полягає в тому, що, засвоївши будову десяткового дробу розрядами, учні не будуть припускатися помилок під час перетворення звичайного дробу на десятковий. Щоб полегшити засвоєння цього питання, можна запропонувати учням декілька пропедевтичних вправ.
1. Прочитайте число 70 549. Як зміниться число, якщо збільшити на 1:
1) останню цифру; 2) передостанню цифру; 3) всі цифри числа.
2. Прочитайте дроби: 0,5; 0,05; 0,005; 0,0005.
Після виконання вправ учні самі можуть здогадатися, що десятковий дріб також є позиційним записом (кожна цифра має певне значення залежно від того, на якому місці (в якому розряді) в запису десяткового числа вона стоїть) і назви розрядів: 1-й розряд після коми — десятих, другий — сотих, третій — тисячних і т. д. (тобто назви «повторюють» назви розрядів натурального числа).
III. Закріплення знань та формування вмінь
@ На цьому уроці учні розв'язують базові завдання на запис і читання десяткових дробів. Слід зауважити, що під час виконання вправ на запис числа, записаного словами десятковим дробом, поданий у підручнику текст краще читати вчителю, роблячи, де потрібно, паузу.
Учням пропонується розв'язати вправи: №№ _________________________
IV. Підсумок уроку
Учитель ще раз нагадує учням, що на уроці вони познайомились зі «скороченою формулою» запису деяких дробів (мішані числа) і (як і під час виконання домашнього завдання) вчилися записувати і читати десяткові дроби.
МАТЕМАТИКА, 5 клас
УРОК № ____ Дата ____________
Тема. Порівняння десяткових дробів
Мета: сформувати в учнів поняття порівняння десяткових дробів та правила порівняння десяткових дробів; умінь порівнювати десяткові дроби, використовуючи правила.
Тип уроку: формування знань учнів.
Обладнання: таблиця «Порівняйте десяткові дроби».
Домашнє завдання п. ___, №№ _________________________
Хід уроку
І. Актуалізація опорних знань
Усні вправи
1. Які числа на координатному промені (рис. 127) відповідають точкам А, В, С, D, E, F?
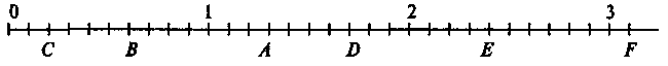 Рис. 127
Рис. 127
2. Порівняйте числа:
1) 3810 і 3809; 2) 53 672 і 53 701; 3) ![]() і
і ![]() ; 4)
; 4) ![]() і
і ![]() .
.
3. Чи правильні рівності?
1) 3 м 6 дм = 3,6 м;
2) 3 км 275 м = 3,275 км;
3) 3 год. 27 хв. = 3,27 год.;
4) 5 кг 75 г = 5,75 кг;
5) 19 ц 7 кг = 19,07 ц;
6) 8 хв. 6 с = 8,6 хв.
II. Формування знань
1. ВЛАСТИВІСТЬ ДЕСЯТКОВОГО ДРОБУ
1. Знайко виміряв довжину шляху від Квіткового містечка до лісу і отримав 0,6 дм. Незнайко виміряв довжину шляху від лісу до Квіткового містечка і отримав 0,60 дм. Чи може так бути? Чому?
Розв'язання. Довжина шляху дорівнює 0,6 дм. Якщо виразити цю довжину у сантиметрах отримаємо 6 см. Але 6 см = 60 мм, а 1 мм = ![]() дм.
дм.
Отже, довжина шляху дорівнює ![]() дм = 0,60 дм, тобто 0,6 дм = 0,60 дм.
дм = 0,60 дм, тобто 0,6 дм = 0,60 дм.
Взагалі, якщо до деякого десяткового дробу дописати справа нуль, то отримаємо дріб, що дорівнює даному, наприклад 0,67 = 0,670 = 0,6700 = 0,67000 і т. д. і навпаки, якщо десятковий дріб закінчується нулем, то цей нуль можна відкинути. Отримаємо дріб, що дорівнює даному, наприклад, 0,800 = 0,80 = 0,8 і т.д.
На закріплення властивості дробу учні виконують вправи №№ 792,793.
2. ПОРІВНЯННЯ ДЕСЯТКОВИХ ДРОБІВ
1) З різними цілими частинами.
2) З рівними цілими частинами, і однаковою кількістю знаків у дробовій частині.
3) З однаковою цілою частиною і з різною кількістю цифр у дробовій частині (цей розділ можна розглянути за підручником).
Сформувавши правила порівняння чисел, учитель робить висновок, що порівняння десяткових дробів можна проводити за алгоритмом:
Порівняння десяткових дробів
1. Порівняй цілі частини.
2. Якщо цілі частини рівні, порахуй кількість цифр у дробовій частині. Якщо кількість цифр рівна, порівняй числа, що стоять у дробових частинах.
3. Якщо кількість цифр у дробових частинах різна, порівняй ці кількості, приписавши необхідну кількість нулів справа в тому дробові, де це необхідно, і порівняй дробові частини. (Показати застосування алгоритму на прикладах таблиці «Порівняйте десяткові дроби».)
Порівняйте десяткові дроби
|
7,305 і 73,05 |
2,5006 і 2,0506 |
|
730,5 і 7305 |
2,0056 і 2,00560 |
|
0,7305 і 0,07305 |
2,506 і 2,50060 |
|
0,0735 і 0,007305 |
2,5006 і 2,50060 |
|
73,05 і 73,050 |
2,56 і 2,560000 |
|
7,3050 і 7,30500 |
25,6 і 25,0600 |
III. Закріплення знань. Вироблення вмінь
На закріплення властивості десяткового дробу і правила порівняння десяткових дробів учні виконують вправи з підручника: №№ ________________
Додаткові задачі
1. Що легше 0,3 кг заліза чи 0,3 кг пір'я?
2. Одного разу вчитель запропонував Незнайку порівняти дроби 0,31 і 0,6. «Це дуже просто, — розпочав Незнайко. — Цілі частини цих дробів рівні. Порівняймо дробові частини. 31 більше за 6, отже, і 0,31 більше за 0,6». Чи згодні ви з цим твердженням?
3. Деяке число задовольняє одночасно три нерівності. Знайдіть це число:
3,5 < □ < 4,1; 3,7 < □ < 4,0; 3,6 < □ < 3,9.
4. У деякому десятковому дробі всі цифри однакові. Який це дріб, якщо він більший за 2,21, але менший від 2,221?
IV. Підсумок уроку
Вчитель ще раз на прикладах повторює правила порівняння десяткових дробів, наголошуючи, що вибір відповідних дій виконується за алгоритмом (див. вище).
1. Прочитайте числа: 13; 1,3; 1,03; 0,13; 0,0013.
2. Якому неправильному дробу дорівнює число?
1) 1,3; 2) 2,5; 3) 7,37; 4) 9,537; 5) 45,77; 6) 35,308.
3. Виразіть: 1) у секундах: 4 хв. 10с; хв..; 2) у хвилинах 5 год. 50 хв.; год.
Тестові завдання
Варіант 1
1. 12 кг 10 г треба записати в кілограмах. Яка з відповідей правильна?
1) 12,1 кг; 2) 1,21 кг; 3) 12,001 кг; 4)12,01 кг.
2. 5 км 42 м треба записати в кілометрах. Яка з відповідей правильна?
1) 5,42 км; 2) 5,042 км; 3) 542 км; 4) 5,402 км.
3. Яке з наведених чисел дорівнює кількості одиниць у розряді тисячних дробу 1,3452?
1) 2; 2) 3; 3) 4; 5) 1.
Варіант 2
1. 3,4 кг треба подати в кілограмах і грамах. Який з наведених записів правильний?
1) 3 кг 4 г; 2) 3 кг 400 г; 3) 3 кг 40 г; 4) 30 кг 4 г?
2. 2 км 23 м треба подати в кілометрах. Який з наведених записів правильний?
1) 2,23 км; 2) 22,3 км; 3) 2,023 км; 4) 2,230 км.
3. Яке з чисел дорівнює кількості одиниць у розряді сотих дробу 0,1234?
1) 1; 2) 3; 3) 4; 4) 2.
Варіант 1
1. 12 кг 10 г треба записати в кілограмах. Яка з відповідей правильна?
1) 12,1 кг; 2) 1,21 кг; 3) 12,001 кг; 4)12,01 кг.
2. 5 км 42 м треба записати в кілометрах. Яка з відповідей правильна?
1) 5,42 км; 2) 5,042 км; 3) 542 км; 4) 5,402 км.
3. Яке з наведених чисел дорівнює кількості одиниць у розряді тисячних дробу 1,3452?
1) 2; 2) 3; 3) 4; 5) 1.
Варіант 2
1. 3,4 кг треба подати в кілограмах і грамах. Який з наведених записів правильний?
1) 3 кг 4 г; 2) 3 кг 400 г; 3) 3 кг 40 г; 4) 30 кг 4 г?
2. 2 км 23 м треба подати в кілометрах. Який з наведених записів правильний?
1) 2,23 км; 2) 22,3 км; 3) 2,023 км; 4) 2,230 км.
3. Яке з чисел дорівнює кількості одиниць у розряді сотих дробу 0,1234?
1) 1; 2) 3; 3) 4; 4) 2.
Варіант 1
1. 12 кг 10 г треба записати в кілограмах. Яка з відповідей правильна?
1) 12,1 кг; 2) 1,21 кг; 3) 12,001 кг; 4)12,01 кг.
2. 5 км 42 м треба записати в кілометрах. Яка з відповідей правильна?
1) 5,42 км; 2) 5,042 км; 3) 542 км; 4) 5,402 км.
3. Яке з наведених чисел дорівнює кількості одиниць у розряді тисячних дробу 1,3452?
1) 2; 2) 3; 3) 4; 5) 1.
Варіант 2
1. 3,4 кг треба подати в кілограмах і грамах. Який з наведених записів правильний?
1) 3 кг 4 г; 2) 3 кг 400 г; 3) 3 кг 40 г; 4) 30 кг 4 г?
2. 2 км 23 м треба подати в кілометрах. Який з наведених записів правильний?
1) 2,23 км; 2) 22,3 км; 3) 2,023 км; 4) 2,230 км.
3. Яке з чисел дорівнює кількості одиниць у розряді сотих дробу 0,1234?
1) 1; 2) 3; 3) 4; 4) 2.
|
7,305 і 73,05 |
2,5006 і 2,0506 |
|
730,5 і 7305 |
2,0056 і 2,00560 |
|
0,7305 і 0,07305 |
2,506 і 2,50060 |
|
0,0735 і 0,007305 |
2,5006 і 2,50060 |
|
73,05 і 73,050 |
2,56 і 2,560000 |
|
7,3050 і 7,30500 |
25,6 і 25,0600 |
|
7,305 і 73,05 |
2,5006 і 2,0506 |
|
730,5 і 7305 |
2,0056 і 2,00560 |
|
0,7305 і 0,07305 |
2,506 і 2,50060 |
|
0,0735 і 0,007305 |
2,5006 і 2,50060 |
|
73,05 і 73,050 |
2,56 і 2,560000 |
|
7,3050 і 7,30500 |
25,6 і 25,0600 |
|
7,305 і 73,05 |
2,5006 і 2,0506 |
|
730,5 і 7305 |
2,0056 і 2,00560 |
|
0,7305 і 0,07305 |
2,506 і 2,50060 |
|
0,0735 і 0,007305 |
2,5006 і 2,50060 |
|
73,05 і 73,050 |
2,56 і 2,560000 |
|
7,3050 і 7,30500 |
25,6 і 25,0600 |
|
7,305 і 73,05 |
2,5006 і 2,0506 |
|
730,5 і 7305 |
2,0056 і 2,00560 |
|
0,7305 і 0,07305 |
2,506 і 2,50060 |
|
0,0735 і 0,007305 |
2,5006 і 2,50060 |
|
73,05 і 73,050 |
2,56 і 2,560000 |
|
7,3050 і 7,30500 |
25,6 і 25,0600 |
МАТЕМАТИКА, 5 клас
УРОК № ____ Дата ____________
Тема. Округлення десяткових дробів
Мета: ознайомити учнів з поняттям округлення чисел до певного розряду; формувати вміння використовувати правило округлення чисел для розв'язання вправ.
Тип уроку: засвоєння нових знань.
Обладнання: таблиця округлення десяткових дробів.
Домашнє завдання п. _______ , №№ ___________________________
Хід уроку
І. Актуалізація опорних знань
Запитання до класу
1. Назвіть розряди числа 53,6171.
2. Знайдіть координати точок, зображених на рис. 129.
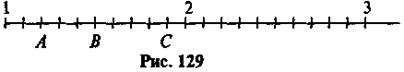
Між якими сусідніми натуральними числами лежать координати точок А, В, С? До якого з натуральних чисел ближче кожне з цих чисел? Які числа знаходяться на однаковій відстані?
3. Знайдіть площу прямокутника зі сторонами:
1) 17 м і 36 м; 2) 29 м і 24 м.
Виразіть цю площу в сотках. Між якими сусідніми натуральними числами знаходяться отримані числа? До якого з них ближче кожне з отриманих чисел?
4. Хлібина коштує 1 грн. 50 к. Скільки коштує 1) півхлібини; 2) чверть хлібини?
II. Мотивація навчальної діяльності
Запитання до класу
1. Чи знаєте ви:
1) Скільки людей живе в Україні?
2) Скільки кубічних метрів містить Чорне море?
3) Скільки волосинок росте на голові людини?
4) Скільки тонн снігу випало торішньої зими?
(Зрозуміло, що більшість учнів не зможе точно відповісти на запитання.)
2. Чи можна знайти точні числа, що є відповідями на попередні запитання?
(Вчитель наголошує, що за певних причин точних відповідей знайти неможливо, тому замість них беруть інші значення, близькі до шуканих, які є круглими і на прикладі досить часто ми маємо справу саме з наближеними значеннями величин.)
Наша мета — встановити правило округлення.
ІІІ. Формування знань учнів про десяткові дроби
Розглянемо числа: 1,2; 1,5; 1,9 — вони мають цілу частину — 1, отже, лежать між сусідніми натуральними числами 1 і 2. Але 1,2 ближче до 1, а 1,9 — до 2. Тому можна сказати, що 1,2 = 1 (приблизно дорівнює 1), а 1,9 = 2. Серед інших десяткових дробів з однією цифрою після коми і цілою частиною 1 є ще кілька чисел, що лежать ближче до 1 (це 1,1; 1,3; 1,4), і кілька чисел, що лежать ближче до 2 (до 1,6; 1,7; 1,8), тому 1,1 = 1; 1,3 = 1; 1,4 = 1, але 1,6 = 2; 1,7 = 2; 1,8 = 2 при цьому можна помітити, що в отриманих числах цифри, що йшли після коми, відсутні, а остання цифра, що залишилась, є цифрою розряду одиниць, і вона співпадає з цифрою розряду одиниць, що були в даному числі, якщо за нею йшли цифри 1; 2; 2; 4, і ця остання цифра збільшилась на 1 у випадку, коли за нею йшли цифри 6, 7, 8, 9.
Цю операцію називають округленням десяткових дробів до < розряду > одиниць і правило, що описує розв'язування подібних задач, можна сформулювати так:
1) Під час округлення десяткового дробу до одиниць (десятих, сотих і т. д.), усі наступні за цим розрядом цифри відкидають.
2) Якщо при цьому перша з цифр, які відкидають, 0,1,2,3,4, то остання з цифр, яку залишають, не змінюється.
3) Якщо ж перша з цифр, які відкидають, дорівнює 5,6,7, 8 або 9, то останню з цифр, яку залишають, збільшують на 1.
(Якщо в учнів виникли запитання про цифру 5, яка не розглядалась у прикладах, варто пам'ятати, що існує домовленість щодо цієї цифри, яка й покладена в правило.)
Після цього варто розглянути, прокоментувати і записати декілька прикладів на округлення. Записи можна робити так:
Приклад 1. Округлити: 1) до одиниць; 2) до сотих; 3) до тисячних число 53,6171.
1) 53,6171 ![]() 54; 2) 53,6171
54; 2) 53,6171 ![]() 53,62; 3) 53,6171
53,62; 3) 53,6171 ![]() 53,617.
53,617.
Зауважимо, що під час округлення натуральних чисел (див. запитання, п. II) правило дещо зміниться, а саме: замість цифр, що стоять у натуральному числі після даного розряду, до якого округляють, пишуть нулі.
Приклад 2. Округлити число 9762:
1) до десятків; 2) до сотень; 3) до тисяч.
1) 9762 ![]() 9760; 2) 9762
9760; 2) 9762 ![]() 9800; 3) 9762
9800; 3) 9762 ![]() 10000.
10000.
IV. Закріплення знань. Формування вмінь
Усні вправи
1. Прочитайте і скажіть, до якого розряду округлили число:
1) 3,543 ![]() 3,5;
3,5;
2) 7,318 ![]() 7;
7;
3) 14,5 ![]() 10;
10;
4) 0,6173 ![]() 0,617.
0,617.
2. Робота з таблицею «Округлення десяткових дробів»
Округліть дроби:
|
до одиниць: |
0,3; 12,7; 26,33; 1,49; |
|
до десятих: |
3,68; 12,05; 23,357; 0,2153; |
|
до сотих: |
15,634; 2,739; 2,6123; 0,0574 |
Письмово за підручником учні виконують вправи №№ ___________________
@ Зауважимо, що не треба вимагати від учнів завчання тексту, виділеного у п. 29 жирним курсивом. Доцільно тільки вимагати засвоєння алгоритму, який можна записати і використовувати у вигляді схеми:
1) Знайди цифру того розряду, до якого округлили десятковий дріб (натуральне число).
2) Подивись на наступну (читаючи зліва направо) цифру; якщо вона 0, або 1, або 2, або 3, або 4 — цифру в п. 1 не змінюй, в інших випадках — збільш її на 1 (+ 1).
3) Усі цифри, що передують знайденій у п. 1, — перепиши, ті, що йдуть за нею, — відкинь (запиши нулями).
V. Підсумок уроку
Запитання до класу
Знайдіть пропущене число (рис. 130)
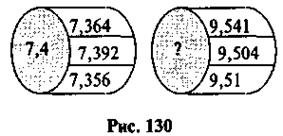
(Пояснюючи, як знайдено правильну відповідь — 9,5, учні повторюють алгоритм округлення чисел.)
Округліть дроби:
|
до одиниць: |
0,3; 12,7; 26,33; 1,49; |
|
до десятих: |
3,68; 12,05; 23,357; 0,2153; |
|
до сотих: |
15,634; 2,739; 2,6123; 0,0574 |
Округліть дроби:
|
до одиниць: |
0,3; 12,7; 26,33; 1,49; |
|
до десятих: |
3,68; 12,05; 23,357; 0,2153; |
|
до сотих: |
15,634; 2,739; 2,6123; 0,0574 |
Округліть дроби:
|
до одиниць: |
0,3; 12,7; 26,33; 1,49; |
|
до десятих: |
3,68; 12,05; 23,357; 0,2153; |
|
до сотих: |
15,634; 2,739; 2,6123; 0,0574 |
МАТЕМАТИКА, 5 клас
УРОК № ____ Дата ____________
Тема. Десятковий дріб.
Мета: вдосконалити вміння учнів розв'язувати задачі, що передбачають виконання порівняння десяткових дробів та перевірити засвоєння знань і вмінь у ході виконання тестових завдань.
Тип уроку: застосування знань і вмінь.
Домашнє завдання п. ____, №№ ____________________________________
Хід уроку
I. Перевірка домашнього завдання
Правильність виконання домашніх вправ можна перевірити в ігровій формі: гра «Знайди помилку». На дошці записані розв'язання домашніх задач, в яких учитель свідомо припускається «типових» помилок. Учні виходять до дошки і виправляють помилки, коментуючи свої дії.
II. Застосування знань
Усні вправи
1. Які з наведених десяткових дробів рівні?
1) 3,205; 2) 3,0250; 3) 3,0025; 4) 3,2050; 5) 3,2005.
2. Порівняйте числа:
1) 1,18 і 1,2; 2) 1,6 і 1,495;
3) 42,004 і 41,005; 4) 10,361 і 10,35;
5) 1,444 і 1,2222; 6) 26,075 і 26,0761.
3. Вкажіть найбільше натуральне значення х, при якому виконується нерівність: 1) 4х < 28,2; 2) 6х < 40,6; 3) х+7 < 12,5.
4. Між якими сусідніми натуральними числами знаходиться дріб?
1) 5,8; 2) 26,75; 3) 35,459.
5. Який знак треба поставити між двома поруч записаними цифрами З, щоб отримати число, яке більше за 3, але менше за 4?
III. Удосконалення знань і вмінь
@ Оскільки дидактична мета уроку — показати учням, що, якими б не були два різних десяткових дроби, завжди можна знайти безліч десяткових дробів, що лежать між двома даними дробами. Усвідомленню цього факту саме присвячені завдання №№ 805 і 807 підручника.
Оскільки на попередньому уроці уроку було розв'язано додаткову задачу № 2 (якщо не було розв'язано, то бажано цей урок розпочати з цього завдання), логічним кроком буде розв'язування спочатку № 807, а потім 805.
Якщо залишиться час, то з метою кращої підготовки до самостійної роботи і попередження помилок, можна запропонувати учням додаткову задачу 1.
Задача 1. Знайдіть помилки і виправте їх:
1) 15,2 > 15,20; 2) 21,307 < 21,3070;
3) 8,911 > 8,191; 4) 0,45 < 0,4050;
5) 8,74 < 8,75; 6) 5,77 < 5,777;
7) 8,49 < 8,50; 8) 0,0005 > 0,005; 9) 4,20 > 4,02.
IV. Тестова робота
Варіант 1
1. Яке з наведених чисел, записаних найменшою кількістю цифр, дорівнює дробу 2,3500?
1) 2,350; 2) 2; 3) 2,35; 4) 2,3.
2. Яка з нерівностей правильна?
1) 14,7 < 14,70; 2) 0,3040 > 0,34;
3) 1,45 > 1,43; 4) 6,307 < 6,037.
3. В якому випадку числа 0,4004, 4,0404; 0,0404; 40,4; 0,404; 4,404 записані в порядку спадання?
1) 0,404; 0,0404; 40,4; 0,4004; 4,404; 4,0404;
2) 40,4; 4,404; 4,0404; 0,404; 0,4004; 0,0404;
3) 0,4004; 4,0404; 0,0404; 40,4; 0,404; 4,404.
4. Між якими сусідніми натуральними числами знаходиться дріб 3,48?
1) 3 і 4; 2) 4 і 5; 3) 4 і 8; 4) 3 і 8.
5. Яке з наведених чисел є розв'язком нерівності 0,2< х< 0,3?
1) 0,4; 2) 0,20; 3) 0,21; 4) 0,32.
Варіант 2
1. Яке з наведених чисел, записаних найменшою кількістю цифр, дорівнює дробу 3,020?
1) 3,2; 2) 3,02; 3) 3; 4) 3,0200.
2. Яка з нерівностей правильна?
1) 3,405 < 3,4050; 2) 3,45 < 3,46;
3) 0,0004 > 0,004; 4) 4,44 < 4,444.
3. В якому випадку числа 2,222; 20,002; 2,22; 2,313; 2,303; 20,201 записані в порядку зростання?
1) 20,201; 20,002; 2,313; 2,303; 2,222; 2,22;
2) 2,22; 2,222; 2,303; 2,313; 20,002; 20,201;
3) 2,222; 2,22; 2,13; 2,303; 20,002; 20,201.
4. Між якими сусідніми натуральними числами знаходиться дріб 12,48?
1) 11 і 12; 2) 12 і 13; 3) 12 і 48; 4) 12 і 14.
5. Яке з наведених чисел є розв'язком нерівності 0,55 < х < 0,56?
1) 0,550; 2) 0,560; 3) 0,557; 4) 0.
Варіант 2
1. Яке з наведених чисел, записаних найменшою кількістю цифр, дорівнює дробу 3,020? 1) 3,2; 2) 3,02; 3) 3; 4) 3,0200.
2. Яка з нерівностей правильна?
1) 3,405 < 3,4050; 2) 3,45 < 3,46;
3) 0,0004 > 0,004; 4) 4,44 < 4,444.
3. В якому випадку числа 2,222; 20,002; 2,22; 2,313; 2,303; 20,201 записані в порядку зростання? 1) 20,201; 20,002; 2,313; 2,303; 2,222; 2,22;
2) 2,22; 2,222; 2,303; 2,313; 20,002; 20,201;
3) 2,222; 2,22; 2,13; 2,303; 20,002; 20,201.
4. Між якими сусідніми натуральними числами знаходиться дріб 12,48?
1) 11 і 12; 2) 12 і 13; 3) 12 і 48; 4) 12 і 14.
5. Яке з наведених чисел є розв'язком нерівності 0,55 < х < 0,56?
1) 0,550; 2) 0,560; 3) 0,557; 4) 0.
Варіант 1
1. Яке з наведених чисел, записаних найменшою кількістю цифр, дорівнює дробу 2,3500? 1) 2,350; 2) 2; 3) 2,35; 4) 2,3.
2. Яка з нерівностей правильна?
1) 14,7 < 14,70; 2) 0,3040 > 0,34;
3) 1,45 > 1,43; 4) 6,307 < 6,037.
3. В якому випадку числа 0,4004, 4,0404; 0,0404; 40,4; 0,404; 4,404 записані в порядку спадання? 1) 0,404; 0,0404; 40,4; 0,4004; 4,404; 4,0404;
2) 40,4; 4,404; 4,0404; 0,404; 0,4004; 0,0404;
3) 0,4004; 4,0404; 0,0404; 40,4; 0,404; 4,404.
4. Між якими сусідніми натуральними числами знаходиться дріб 3,48?
1) 3 і 4; 2) 4 і 5; 3) 4 і 8; 4) 3 і 8.
5. Яке з наведених чисел є розв'язком нерівності 0,2< х< 0,3?
1) 0,4; 2) 0,20; 3) 0,21; 4) 0,32.
Варіант 2
1. Яке з наведених чисел, записаних найменшою кількістю цифр, дорівнює дробу 3,020? 1) 3,2; 2) 3,02; 3) 3; 4) 3,0200.
2. Яка з нерівностей правильна?
1) 3,405 < 3,4050; 2) 3,45 < 3,46;
3) 0,0004 > 0,004; 4) 4,44 < 4,444.
3. В якому випадку числа 2,222; 20,002; 2,22; 2,313; 2,303; 20,201 записані в порядку зростання? 1) 20,201; 20,002; 2,313; 2,303; 2,222; 2,22;
2) 2,22; 2,222; 2,303; 2,313; 20,002; 20,201;
3) 2,222; 2,22; 2,13; 2,303; 20,002; 20,201.
4. Між якими сусідніми натуральними числами знаходиться дріб 12,48?
1) 11 і 12; 2) 12 і 13; 3) 12 і 48; 4) 12 і 14.
5. Яке з наведених чисел є розв'язком нерівності 0,55 < х < 0,56?
1) 0,550; 2) 0,560; 3) 0,557; 4) 0.
Варіант 1
1. Яке з наведених чисел, записаних найменшою кількістю цифр, дорівнює дробу 2,3500? 1) 2,350; 2) 2; 3) 2,35; 4) 2,3.
2. Яка з нерівностей правильна?
1) 14,7 < 14,70; 2) 0,3040 > 0,34;
3) 1,45 > 1,43; 4) 6,307 < 6,037.
3. В якому випадку числа 0,4004, 4,0404; 0,0404; 40,4; 0,404; 4,404 записані в порядку спадання? 1) 0,404; 0,0404; 40,4; 0,4004; 4,404; 4,0404;
2) 40,4; 4,404; 4,0404; 0,404; 0,4004; 0,0404;
3) 0,4004; 4,0404; 0,0404; 40,4; 0,404; 4,404.
4. Між якими сусідніми натуральними числами знаходиться дріб 3,48?
1) 3 і 4; 2) 4 і 5; 3) 4 і 8; 4) 3 і 8.
5. Яке з наведених чисел є розв'язком нерівності 0,2< х< 0,3?
1) 0,4; 2) 0,20; 3) 0,21; 4) 0,32.
МАТЕМАТИКА, 5 клас
УРОК № ____ Дата ____________
Тема. Округлення десяткових дробів. Розв´язування типових вправ.
Мета: закріпити знання алгоритму округлення десяткового дробу до повного розряду; відпрацювати навички розв'язування задач, що передбачають застосування округлення чисел.
Тип уроку: засвоєння навичок та вмінь.
Домашнє завдання: п.____ , №№ __________________________________.
Хід уроку
І. Перевірка домашнього завдання
II. Відтворення знань учнів
Усні вправи
1. Округліть:
1) до десятих: 8,435; 32,1601; 9,75;
2) до сотих: 65,1783; 4,008; 1,6666;
3) до одиниць: 50,92; 1,19; 8,47;
4) до сотень: 438; 3078,65; 196,48.
2. Які з чисел: 0,7; 0,8; 0,78; 0,8001; 0,85; 0,876; 0,8999; 0,9; 0,9000001 задовольняють нерівність 0,8 < х < 0,9?
3. За ![]() кг сиру заплатили 5 грн. Скільки треба заплатити за 2
кг сиру заплатили 5 грн. Скільки треба заплатити за 2![]() кг такого сиру?
кг такого сиру?
III. Відпрацювання навичок
Учням можна запропонувати розв'язати задачі достатнього рівня, які, окрім усього іншого, передбачають виконання округлення дробів
№№ __________________ вправи, обернені до вправ на округлення десяткових дробів (тобто на відновлення даного числа за відомим наближеним значенням), та декілька вправ більш високого рівня складності (додаткові задачі №№ 1-5)
Додаткові задачі
1. Знайдіть помилку:
1) 3,27 ![]() 3,3; 2) 2,99
3,3; 2) 2,99 ![]() 3,0;
3,0;
3) 12,34 ![]() 12,3; 4) 0,75
12,3; 4) 0,75 ![]() 0,7;
0,7;
5) 8,18 ![]() 8,2.
8,2.
2. Усі числа: 2,5; 2,6; 2,7; 2,8; 2,9; 3,1; 3,2; 3,3; 3,4 – мають одну особливість, пов'язану з округленням чисел. Яку?
3. Незнайко задумав число. Спочатку він округлив це число до десятих, отримав 6,4. Потім він округлив задумане число до одиниць, отримав 7. Чи не помилився він?
4. Знайдіть пропущений рисунок:
|
3,654 |
|
8,34 |
|
1,35 |
? |
4,7 |
5. Знайдіть пропущене число:
9,7 2а – 3 = 17;
4,1 5а – 8 = 2а + 4;
5,3 28 – 4a = ?
IV. Підсумок уроку
Усні вправи
1. Записати у вигляді звичайного дробу: 0,3; 0,32; 0,03; 1,725; 2,374.
2. Виконати дії: 1) 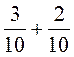 ; 2)
; 2) 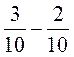 ; 3)
; 3) 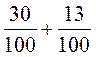 ; 4)
; 4) 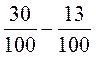 ;
;
5) 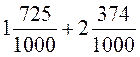 ; 6)
; 6) 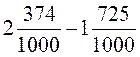 .
.
3. Записати всі числа з однаковою кількістю цифр у дробових частинах:
1,2; 0,03; 13,170.
4. Обчислити: 1) 7 + 15; 2) 70 + 15; 3) 7 + 150; 4) 70 + 150; 5) 15 – 7;
6) 150 – 7; 7) 70 – 15; 8) 150 – 70.
5. Розв'язати рівняння: 1) 27 + х = 35; 2) 35 – х = 27; 3) х – 27 = 35.


про публікацію авторської розробки
Додати розробку