Конспект уроку "Скалярні і векторні величини"

Тема уроку: Скалярні та векторні величини

Мета уроку:

•    Ознайомлення учнів з математичним апаратом у курсі фізики, формування знань учнів про скалярні та векторні величини, вміння проводити дії над векторами;
•    розвиток умінь учнів доречно та коректно вживати в мовленні фізичну термінологію, чітко, лаконічно та зрозуміло формулювати думку; поповнювати свій словниковий запас;
•    виховувати здатність до відстоювання власної думки, уміння підводити підсумки чужої та власної роботи.

Тип уроку: комбінований.

Обладнання та наочність:

• підручник «Фізика 10 клас», рівень стандарту. В.Г.Бар’яхтар, С.О.Довгий, 2018 р.,
• PowerPoint презентація до уроку,
•  https://www.youtube.com/watch?v=py14nKD28RQ

Хід уроку

I. Організаційний момент.

1. Бесіда за питаннями

1. Назвіть основні методи фізичних досліджень. Наведіть приклади.
2. Наведіть приклади фізичних моделей. Чому фізична модель – це ідеалізований об’єкт?
3. Назвіть основні одиниці СІ та величини, для вимірювання яких вони слугують.
4. Які види похибок вимірювань ви знаєте?
5. Як визначити випадкову похибку вимірювання?
6. Чим визначається абсолютна систематична похибка?
7. Що називають відносною похибкою вимірювання?
8. Як правильно округлити й записати результати вимірювань?

II. Актуалізація опорних знань.

Фронтальне опитування

1. Яку мову використовують учені для опису природи?
2. Що таке вектор?
3. Де застосовують вектори?

III. Вивчення нового матеріалу

Мотивація навчальної діяльності учня

До розуміння того, що для описування природи потрібно використовувати мову математики, учені дійшли давно. Власне, певні розділи математики було створено для того, щоб описувати природу стислою й доступною мовою. Так, для визначення миттєвої швидкості, роботи змінної сили, об'єму тіл неправильної форми та ін. було створено диференціальне та інтегральне числення. Для наочнішого описування фізичних процесів навчилися будувати графіки функцій, а для швидкої обробки результатів експерименту придумали методи наближених обчислень.

1. Скалярні та векторні величини.

У сучасній фізиці застосовують математичні величини різних типів, зокрема скалярні та векторні.

Скалярні величини – це величини, які визначаються тільки значенням.

(Густина води дорівнює 1000 кг/м³, а тривалість земної доби – 24 год)

Додати дві скалярні фізичні величини означає додати їхні значення, подані в однакових одиницях (наприклад, не можна додавати масу до часу, а густину до роботи тощо).

Векторні величини – це величини, які мають значення (модуль) і напрямок.

Вектор – це напрямлений відрізок, тобто відрізок, що має і довжину, і напрямок.

Модуль вектора – це довжина напрямленого відрізка.

Позначають векторні величини літерами грецького та латинського алфавітів, над якими поставлено стрілки.

позначає вектор швидкості, а – модуль швидкості

Суму двох векторів визначають за правилом паралелограма або правилом трикутника.

Визначення суми двох векторів і за правилом паралелограма:

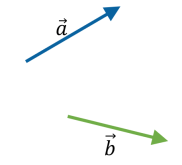
Визначення суми двох векторів і за правилом трикутника:

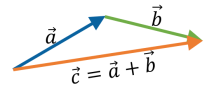
Як визначити суму кількох векторів?

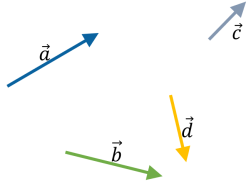
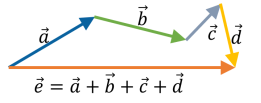
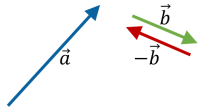
Як визначити різницю двох векторів?

1-й спосіб

До вектора додають вектор, протилежний вектору : , тобто

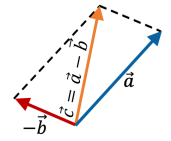
2-й спосіб

Вектори і розміщують так, щоб вони виходили з однієї точки, вектор , що з’єднує кінець вектора із кінцем вектора , і є вектор різниці векторів і , тобто

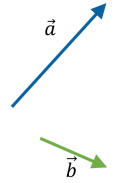
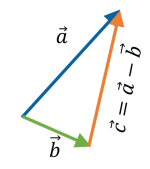
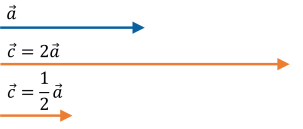
Що вийде у результаті множення векторної величини на скалярну?

У результаті множення векторної величини на скалярну величину k виходить вектор

Якщо , вектори і співнапрямлені.

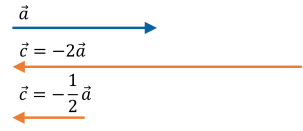
Якщо , вектори і напрямлені протилежно.

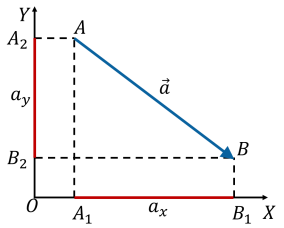
Проекції вектора на осі координат

Як знайти проекції вектора на осі координат?

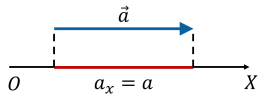
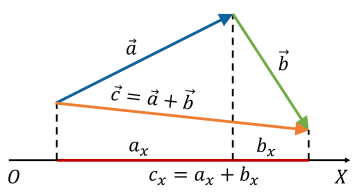
Визначення проекцій вектора на осі координат:

– проекція вектора на вісь

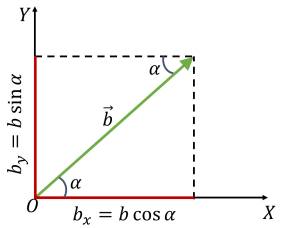
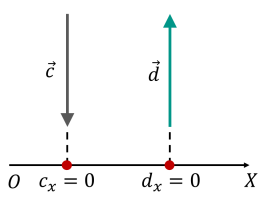
– проекція вектора на вісь

IV. Засвоєння нових знань і способів дій

№1. Чи можна додавати площу й об’єм? вектор імпульсу й енергію? вектор швидкості та вектор сили? енергію та роботу? Чому?

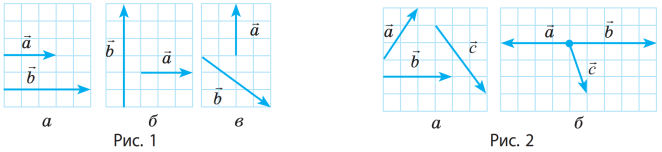
№2. Перенесіть у зошит рис. 1. Для кожного випадку знайдіть суму та різницю двох векторів.

№3. Перенесіть у зошит рис. 2. Для кожного випадку знайдіть суму трьох векторів.

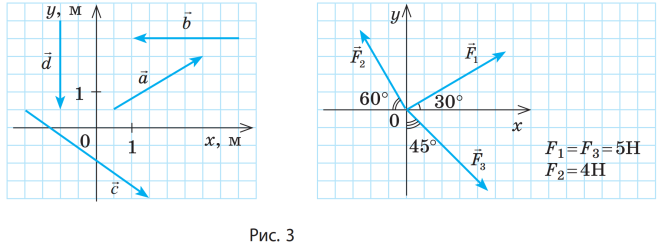
№4. Визначте проекції векторів на осі координат (рис. 3).

V. Підбиття підсумків уроку, рефлексія

Бесіда за питаннями

1. Які фізичні величини називають скалярними? векторними? Наведіть приклади.
2. Як знайти суму векторів? різницю векторів? добуток вектора та скаляра?
3. Як знайти проекції вектора на осі координат?

VI. Домашнє завдання
(§3, № 3 завдання 3, рис.2)