Тема уроку: ЛАБОРАТОРНА РОБОТА

 Визначення прискорення вільного падіння тіл

Мета роботи. З’ясувати роль сили тяжіння в природі, освоїти метод визначення g за допомогою математичного маятника, визначити чисельне значення g.

Прилади і приладдя: математичний маятник зі змінною довжиною нитки, масштабна лінійка, годинник.

Матеріал, який необхідно засвоїти перед виконанням роботи: 

1) Прискорення поступального руху.

 2) Закони Ньютона.

3) Сили тяжіння.

4) Вага тіл.

5) Прискорення вільного падіння.

 6) Невагомість.

 7) Коливальний рух та його характеристики.

8) Динаміка коливального руху.

 9) Маятник.

Теоретичні відомості

Прискоренням вільного падіння називають прискорення, з яким тіло рухається до Землі, коли на нього діє тільки сила земного тяжіння.

Прискорення вільного падіння тіл (g) – одна з фундаментальних фізичних величин, що пояснює низку важливих процесів в оточуючому людину світі. Зокрема, його чисельне значення, разом із значенням маси (m), визначає вагу тіла (P = mg).               Прискорення, з якими рухаються тіла, в тому числі й прискорення вільного падіння, завжди зумовлені силами, що діють на тіла.

Прискорений рух може викликати такі особливі стани тіл, як перевантаження і невагомість. Перевантаження суттєво впливають на процеси в живих організмах, змінюючи тиск внутрішніх органів один на одного, викликають відтік крові, деформацію складових частин тощо. Невагомість має місце при вільному падінні тіл, або коли діючі на тіло сили взаємо компенсуються. Як і перевантаження, невагомість змінює хід процесів у біологічних об’єктах.

Прискорення, з яким тіла падають на Землю, зумовлене силою їх притягання до неї. Притягання фізичних тіл одне до одного є загальною властивістю матерії й існує як між макроскопічними тілами (зірками, планетами), так і між мікроскопічними тілами (атоми, молекули). Узагальнюючи відомі експериментальні факти, Ньютон сформулював закон всесвітнього тяжіння.

Дві матеріальні точки притягуються одна до другої із силою F, прямо пропорційною їх масам m₁ і m₂ і обернено пропорційною квадрату відстані r між ними:

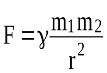, (1)

де γ – гравітаційна стала, що дорівнює 6,67×10^-11.

Гравітаційна стала чисельно дорівнює силі взаємодії двох матеріальних точок з масами 1 кг, що знаходяться одна від одної на відстані 1 м.

Формула (1) справедлива і для реальних тіл, що мають сферичну форму. У цьому випадку r – відстань між центрами сфер.

Вона справедлива і для взаємодії тіл сферичної форми з великим радіусом і тіл будь-якої форми, але невеликих, порівняно зі сферою, розмірів. Тоді r – відстань від центру сфери до тіла.

Маса m у формулі (1) є характеристикою гравітаційних властивостей взаємодіючих тіл. Ця взаємодія між тілами здійснюється через гравітаційне поле за наступною схемою: перше тіло створює поле, яке діє на друге тіло, а друге тіло своїм полем діє на перше тіло.

Гравітаційна взаємодія Землі з будь-яким тілом, що знаходиться біля її поверхні, проявляється в притягуванні його Землею. Якщо тіло знаходиться на висоті (h) від поверхні Землі, то на нього діє сила тяжіння:

F = 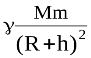, (2)

де R – радіус Землі, приблизно рівний 6400 км; М – маса Землі; m – маса тіла.

Якщо h << R, то h можна знехтувати і формула (2) приймає вигляд:

F = 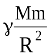. (3)

Цю ж силу можна виразити і через прискорення a, з яким тіло падає на Землю:

F = ma; (4)

Із формул (3) і (4) випливає:

a = 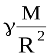. (5)

Оскільки γ, M, R – сталі, то і прискорення, з яким тіла падають на Землю у вакуумі, є сталою величиною. Його позначають буквою g, а чисельно воно приблизно дорівнює 9,8 м/с²

Взагалі значення g залежить від висоти h над рівнем моря і географічної широти. Остання залежність зумовлена тією обставиною, що Земля являє собою "приплюснутий" з полюсів шар, що обертається. Внаслідок добового обертання Землі з кутовою швидкістю ω навколо власної осі, що проходить через її полюси, виникає відцентрова сила інерції, яка зменшує величину прискорення вільного падіння g.

Неідеальна кулеподібність Землі та її добове обертання зумовлює те, що величина g в різних місцях Землі змінюється від 9,8м/с² на полюсах, до 9,78м/с² на екваторі.

Якщо тіло знаходиться на якійсь опорі, чи підвішене, то внаслідок притягання до Землі воно діє з певною силою на опору, або розтягує 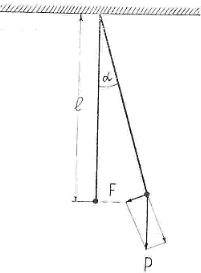підвіс.

Вагою тіла називають силу, з якою тіло діє на опору або розтягує підвіс, внаслідок притягання тіла до Землі.

Вагу тіла позначають буквою Р і відповідно до другого закону Ньютона, вона дорівнює:

P = mg.

Якщо тіло вільно падає на Землю, тобто не діє на опору і не підвішене, то його вага дорівнює нулю, тобто тіло знаходиться в стані невагомості.

Існують різні методи експеримен-тального визначення g. Одним із таких є метод, в якому використовують вимірювання характеристик коливань математичного маятника.

Математичним маятником нази-вають матеріальну точку, що коливається на тонкій, невагомій нитці, яка не деформується.

Математичний маятник здійснює гармонійні коливання під дією квазіпружної сили – сили тяжіння Р

При гармонійних коливаннях фізична величина х, що коливається, змінюється з часом за законом:

х = A sin (ωt + α₀),

де А – амплітуда коливань; ωt + α₀ – фаза коливань; α₀ – початкова фаза; ω – кругова частота; t – час коливань. У випадку коливань математичного маятника, х – зміщення від рівноважного положення.

Амплітудою коливань називають найбільше абсолютне значення фізичної величини, що коливається.

Частотою періодичних коливань ν називається число повних коливань, що відбуваються за одиницю часу.

Частота ν і кругова частота ω зв’язані співвідношенням:

ω = 2πν.

Періодом коливань називають час T, за який відбувається одне повне коливання.

Період Т при малих відхиленнях маятника залежить від довжини маятника l:

T = . (5)

Звідси:

g =. (6)

Таким чином, якщо відомі значення l і Т, то користуючись формулою (6), можна знайти чисельне значення прискорення вільного падіння тіл g.

Порядок виконання роботи:

1.               Визначити l – довжину маятника за допомогою вертикальної шкали.
2.               Відхилити маятник на малий кут (5°–10°) і визначити час 10 повних коливань t. Знайти період коливань Т за формулою: Т = t/10. Виміри повторити тричі при різних значеннях l.
3.               Дані вимірювань занести в таблицю.
4.               За формулою (6) знайти значення g, підставляючи в неї l та Т.

Таблиця:

5. Висновок: