Лінійна функція,її графік та властивості

7 клас. Тема: Лінійна функція,її графікта властивостіБондарчук К. Д. Мета уроку:навчальна: сформувати поняття лінійної функції,формувати вміння будувати графік лінійної функції,виділити основні властивості лінійної функції;розвивальна:розвивати спостережливість, кмітливість,уміння опрацьовувати графічну інформацію на прикладі практичного завдання.

Чи є задана відповідність функцією?

Знайдіть область визначення функції: А) у = . Б) у = В) у = х ≠5 R R Область визначення функції у=kx+b є будь - яке число, х є R.-4х +7.

Перевірка домашнього завдання “ Лови помилку!”Не будуючи графік, знайдіть нулі функції:1) у=-2х;2) у=6- 3х;3) у= х²-4;4) у=Відповіді1) х=02) х=23) х=-2,х=24) х=-3style.colorfillcolorfill.type

Маса одного яблука 0,25 кг, а маса порожньої корзини 3 кг. Яка маса корзини з яблуками разом ? Нехай у корзині х яблук У кг - маса корзини з яблуками Маємо залежність , яку можна задати формулоюy = 0,25x + 3 3кг Маса корзини

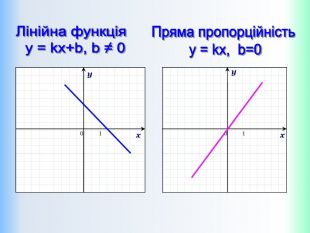
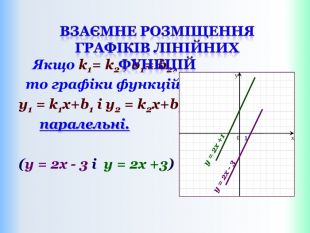
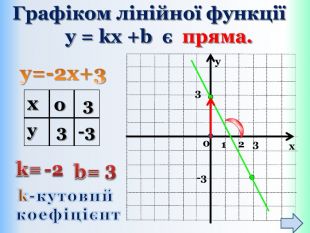
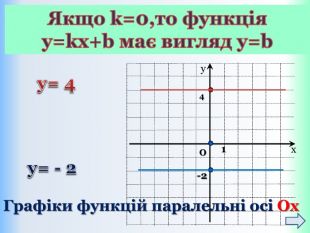
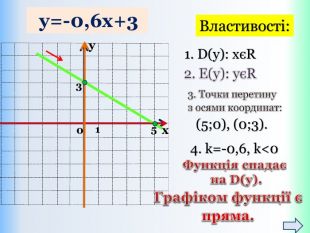
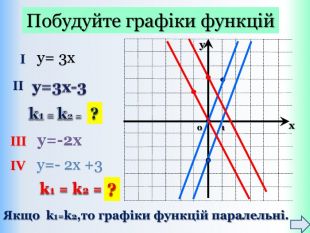
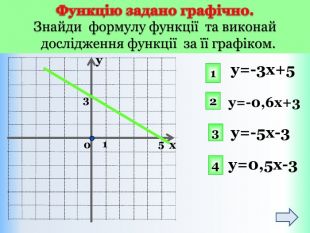
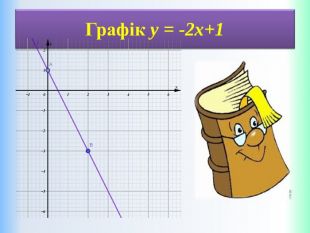
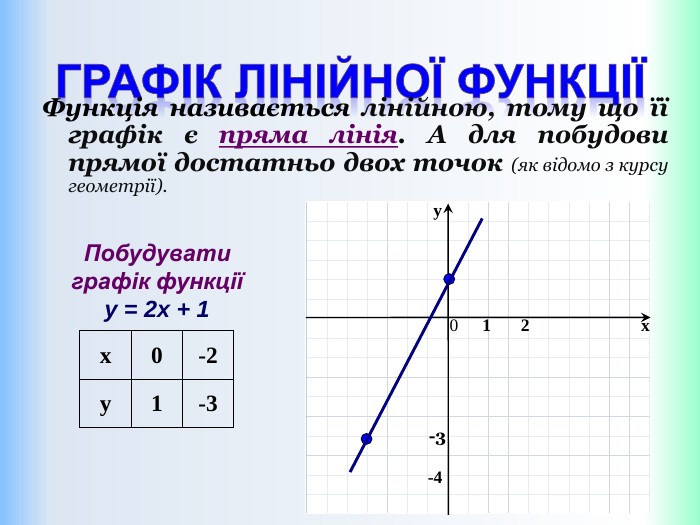
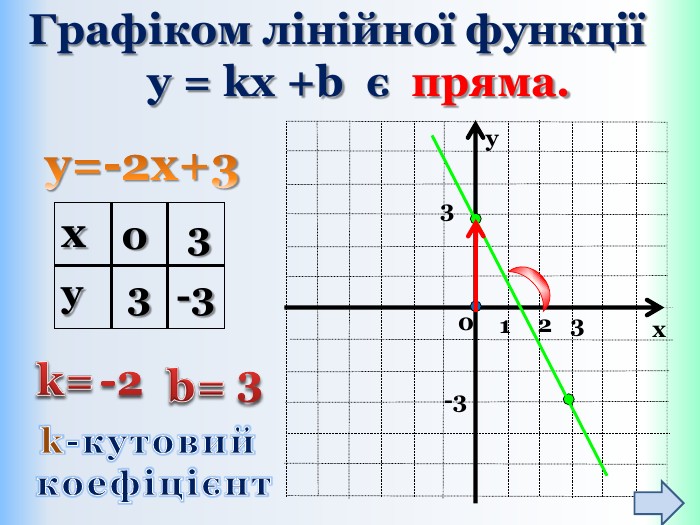
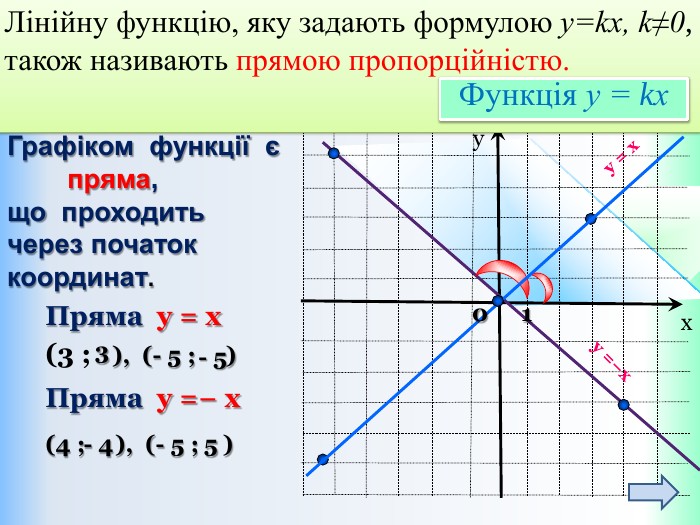
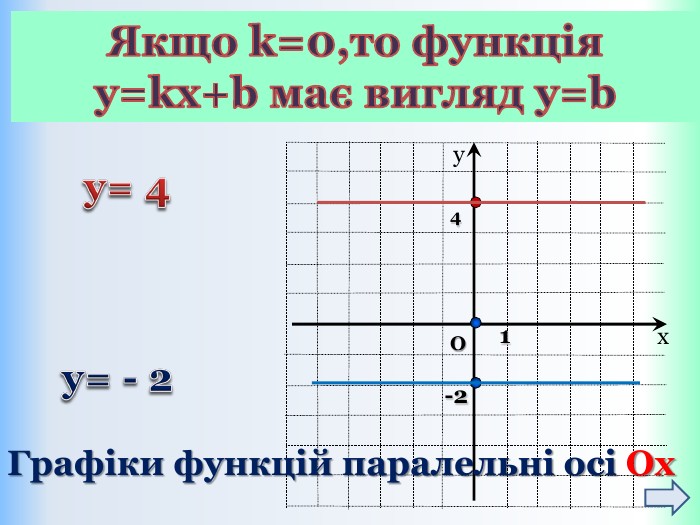
Функцію, яку можна задати формулою виду y = kx + b, де k і b – деякі числа, x – незалежна змінна, називають лінійною. Означення: Приклади лінійних функцій: Y = 2x-9; y = -1/5x; y = -1; y = 5 - x. Областю визначення лінійної функції – є всі дійсні числа, тобто обмежень на аргумент немає!Областю значень лінійної функції – є всі дійсні числа, тобто обмежень на функцію (залежну змінну) немає! ppt_xxshearppt_x

Графік лінійної функціїФункція називається лінійною, тому що її графік є пряма лінія. А для побудови прямої достатньо двох точок (як відомо з курсу геометрії).xy01-42 Побудуватиграфік функції y = 2x + 1x0-2y 1-3-3

0101 Лінійна функція y = kx+b, b ≠ 0 Пряма пропорційність y = kx, b=0уухх

Якщо k1≠ k2, то графіки функцій y1 = k1x+b1 і y2 = k2x+b2 перетинаються в одній точці. ( у = х + 4 і у = - х + 4)Взаємне розміщенняграфіків лінійних функційxy0

Якщо k1= k2 , b1≠ b2, то графіки функцій y1 = k1x+b1 і y2 = k2x+b2 паралельні.(у = 2х - 3 і у = 2х +3)Взаємне розміщенняграфіків лінійних функційxy0 1у = 2х +1у = 2х - 3

xy01xy01xy01xy01y = xy = - xy = | x |y = ax = m. Корисно пам'ятати

Лінійна функція-це функція виду у=kх +b, де х –незалежна змінна, k і b – деякі числабy=-x+4y=0,9xy=x²-5xy=3-7xy= 6y-2x+5=0y=4x-5 Знайдіть лінійні функції і зроби клік мишею по формулійн. Ліцеу=8x-9мrppt_x

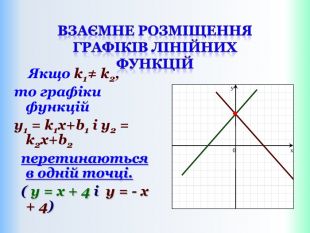
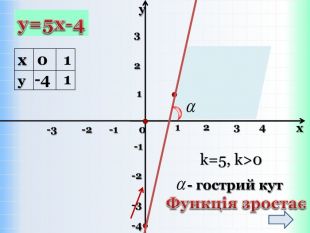
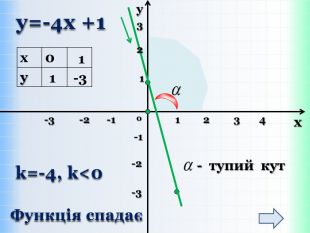
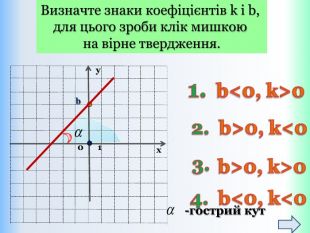
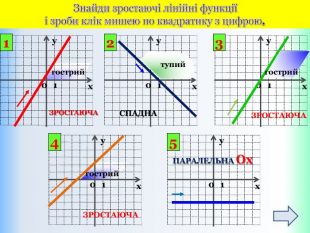
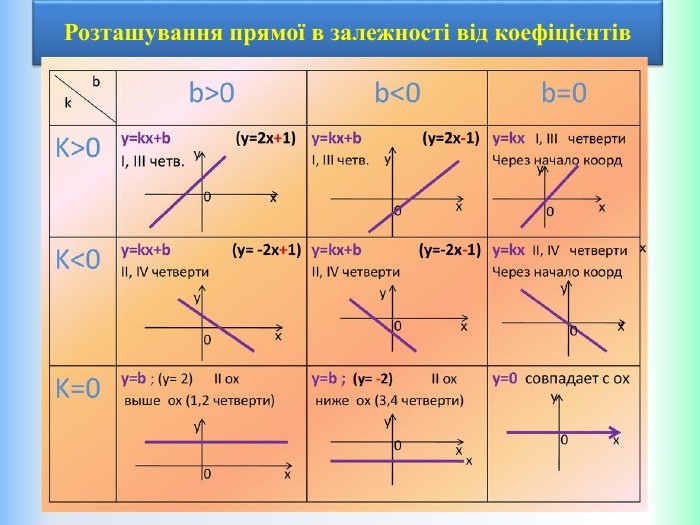
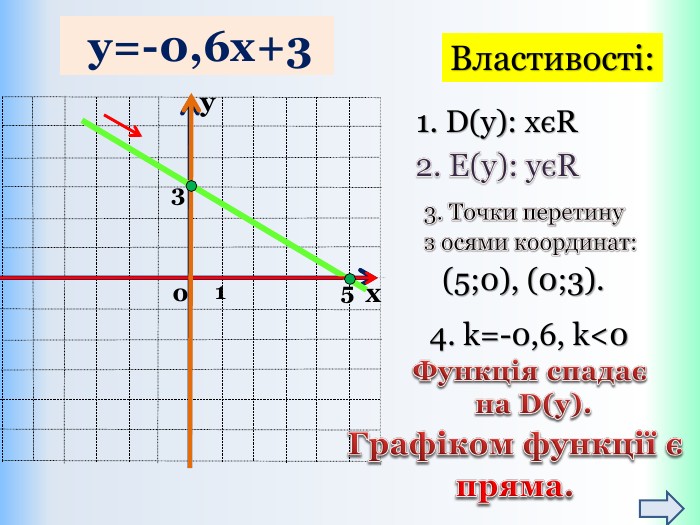
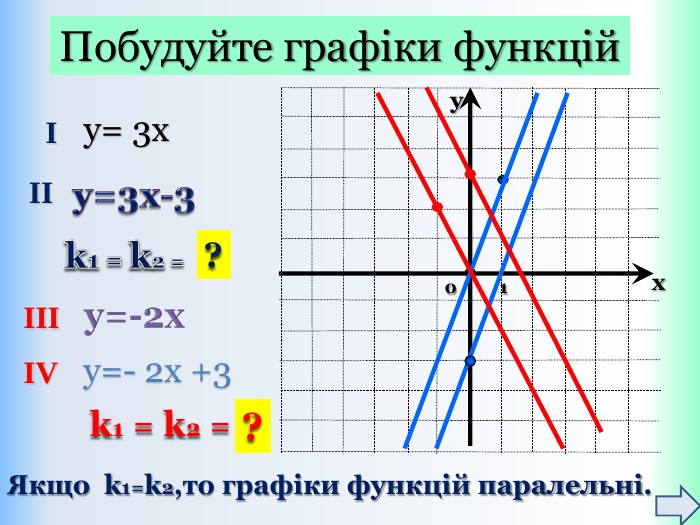
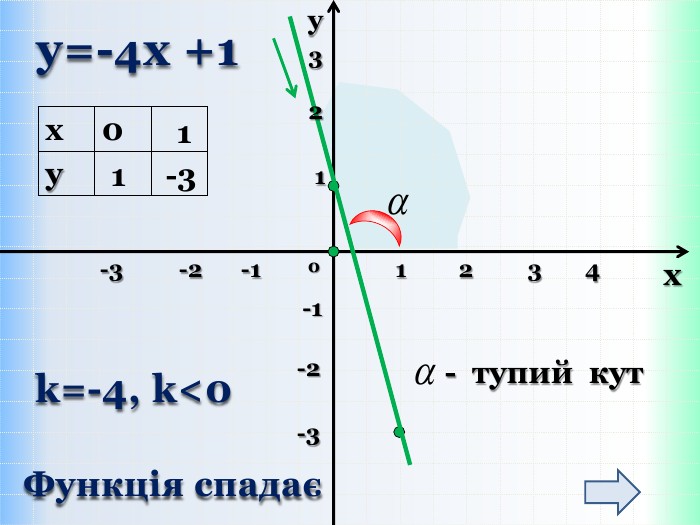
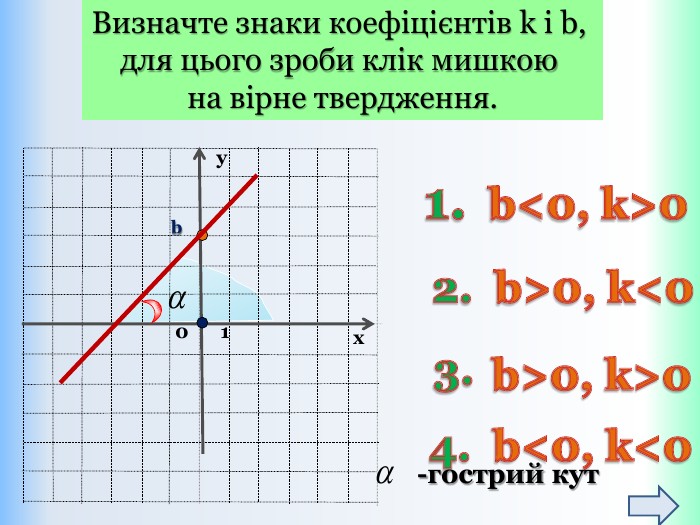
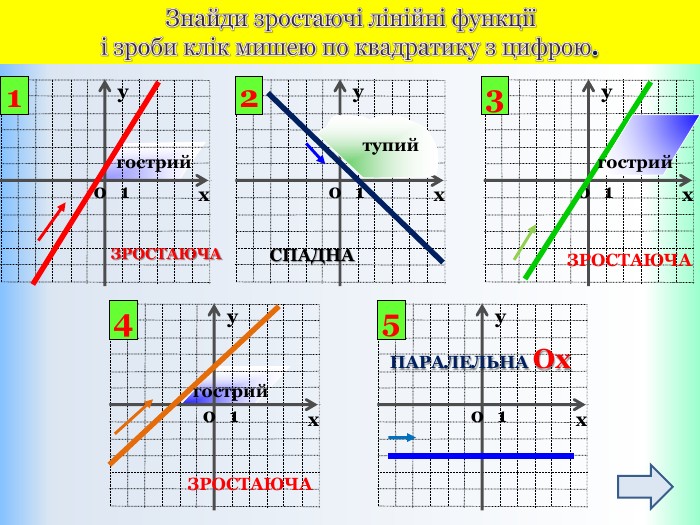
{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Властивості функції Види функції ( k≠0) y=kx +b, k>0 y=kx+b,k<0 Область визначення. Всі числа (х є R)Всі числа (х є R)Множина значень. Всі числа (у є R)Всі числа (у є R)Додатні значення x> - x< - Від‘ємні значення x< - x> - Проміжки зростання. Всі числа (х є R)------------------------Проміжки спадання------------------------------Всі числа (х є R)

Розташування прямої в залежності від коефіцієнтів

01ух32-33 Графіком лінійної функції y = kх +b є пряма.y=-2x+3{5940675 A-B579-460 E-94 D1-54222 C63 F5 DA}xyk=b=033-3-23k-кутовий коефіцієнт

Письмова вправа. Визначити, чи є лінійною функцією, задані формули? Якщо відповідь стверджувальна, то вказати коефіцієнти k і b. Приклад: y = -3x + 1. Функція лінійна, тому що можна задати формулою y = kx+b . Коефіцієнти k = -3, b = 1.1) y= 8 – 7x2) y = x/3 + 23) y = 3/x + 2 4) y = 2x² + 45) y = - 46) y = (12x – 8)/4

ВІДПОВІДІ: Лінійними функціями є: k=-7, b=8;k=1/3,b=2;5) k=0,b=-4;6) k=3, b=-2.

01ух423-4y=x+4{5940675 A-B579-460 E-94 D1-54222 C63 F5 DA}xy -1k=1b=40-143 Побудувати графік функції

Графіком функції є пряма, що проходитьчерез початок координат. Пряма y = x(3 ; ), (- 5 ; )Пряма y =− x(4 ; ), (- 5 ; )- 5 3- 4хуy = xy =−x501 Лінійну функцію, яку задають формулою y=kx, k≠0, також називають прямою пропорційністю. Функція у = kх ppt_xxshearppt_x

Якщо k=0,то функціяy=kx+b має вигляд у=bху. О14-2у= 4у= - 2 Графіки функцій паралельні осі Ох

ху0153 у=-0,6х+31. D(y): хєRВластивості:2. Е(у): уєR 3. Точки перетину з осями координат:(5;0), (0;3).4. k=-0,6, k<0 Функція спадає на D(y). Графіком функції є пряма.

ху. Побудуйте графіки функційу= 3ху=-2ху=3х-3у=- 2х +3 III k1 = k2 =IIIIVk1 = k2 =Якщо k1=k2,то графіки функцій паралельні.??10style.colorfillcolorfill.typefill.onrrrrrstyle.colorfillcolorfill.typefill.onrrrrr

xу-1-20123-3-41234-1-3-2у=5х-4{5940675 A-B579-460 E-94 D1-54222 C63 F5 DA}хуk=5, k>0 Функція зростає- гострий кут011-4

-1-3-21234 1 2 3-1-2-30y=-4х +1{5940675 A-B579-460 E-94 D1-54222 C63 F5 DA}х0 ууxk=-4, k<0 Функція спадає- тупий кут1-31

Визначте знаки коефіцієнтів k і b, для цього зроби клік мишкою на вірне твердження.01ухb1. b<0, k>02. b>0, k<0b>0, k>04. b<0, k<0-гострий кут3.

01ухb-тупий кут1. b<0, k>02. b>0, k>0b<0, k<03. b>0, k<0 Знайди правильну відповідь4.

01ухгострий. ЗРОСТАЮЧА101ух. СПАДНА201ух. ЗРОСТАЮЧА301ух01ухгострий. ЗРОСТАЮЧАПАРАЛЕЛЬНА Ох45 Знайди зростаючі лінійні функції і зроби клік мишею по квадратику з цифрою.тупийгострий

ху0153 Функцію задано графічно. Знайди формулу функції та виконай дослідження функції за її графіком. 1у=-3х+52у=-0,6х+33у=-5х-34у=0,5х-3style.colorstyle.colorstyle.colorstyle.color

Побудуйте графік функціїОбласть визначення: х≠3 Графіком цієї функції є пряма, з якої виключена точка з координатою (3;6)

х. У030-3ху013-36

Побудуйте графік функціїПеретворення ГРАФІК01ух 2 2-2

Дорогу осилить той, хто йде. Спасибі за урок.ppt_x

Домашнє завдання: Стор.160 §23 опрацювати, розглянути приклади: 3, 4, № 850, 853, 855

Письмові вправи в зошитіФункцію задано формулою y=-2x+5. Знайдіть: а) значення функції, якщо значення аргументу дорівнює: -4; 3,5;0; б) значення аргументу, при якому значення функції дорівнює: 9; -5; 0. Побудуйте графік функції: а) y=3x+1; б) y= -1∕6 ·x – 2; в) y=-2x

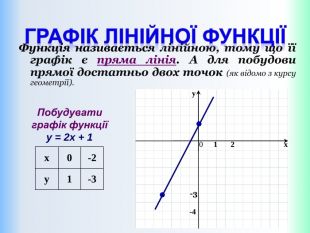
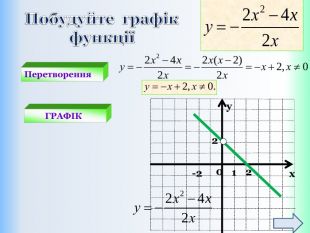
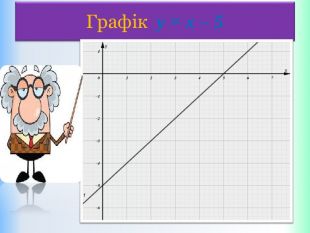
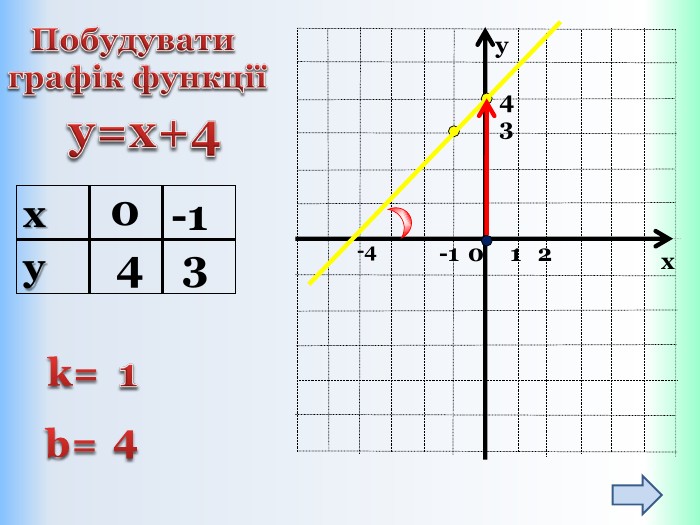
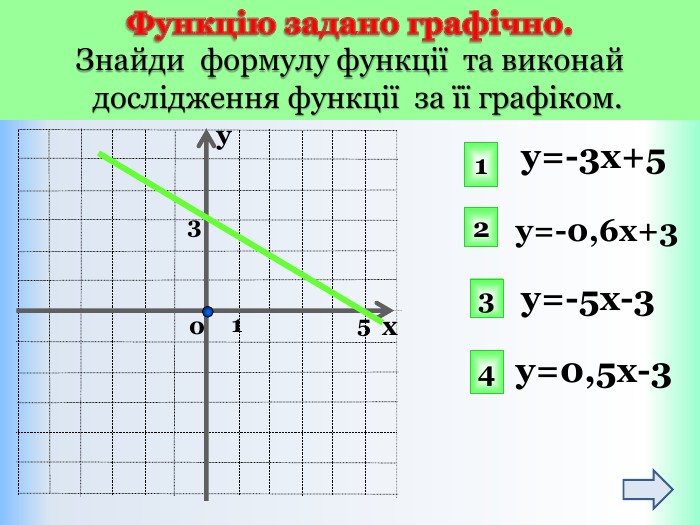
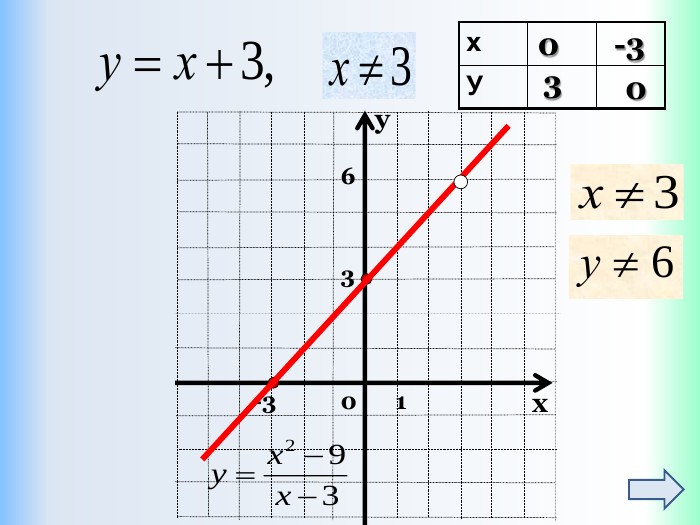
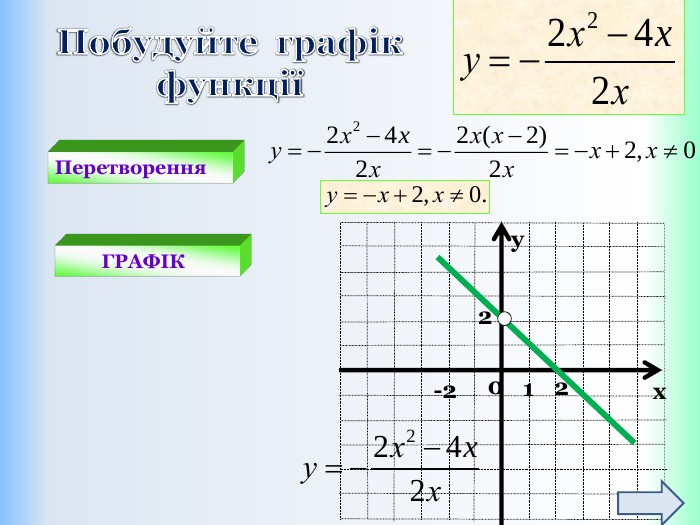
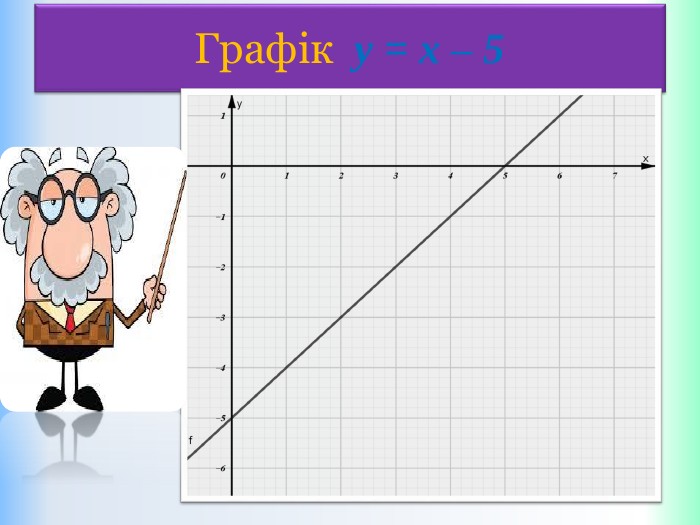
Письмове завдання: Побудуйте графік функції y = x – 5. Розв’язання: Складемо таблицю значень даної функції для двох довільних значень аргументу. Значення х беремо будь-які, але зручні, щоб точки з вибраними координатами можна було побудувати в зошиті. Які б не взяли х, обчислюємо у і отримаєте графік!{5 DA37 D80-6434-44 D0-A028-1 B22 A696006 F}xystyle.colorfillcolorfill.type

Графік y = x – 5

Графік y = -2x+1

Домашнє завдання№ 893,896,907Істер О. С. Алгебра: підручник для 7 кл.загальноосвіт.навч.закл.-К.: Освіта,2007.-223с.