Лінійне рівняння з двома змінними та його графік

Лінійне рівняння з двома змінними та його графік Підготувала вчитель математики Городянської гімназіїСтефурак Галина Василівна

Повторення1. Яку функцію називають лінійною?2. Що є графіком лінійної функції?Лінійною функцією називають функцію, яку можна задати формулою виду y = kx + b, де х– незалежна змінна, k і b – деякі числа. Графіком лінійної функції є пряма.3. Координати скількох точок достатньо визначити, щоб побудувати графік лінійної функції?Для побудови прямої достатньо знайти координати двох точок.

Запам’ятаймо. Рівняння виду ах + bу = с , де a, b, с — дані числа, називаєть­ся лінійним рівнянням з двома змінними. Рівняння виду ах + bу= с, де а≠0 і b≠0, називається рів­нянням першого степеня з двома змінними. Наприклад, 2х + 3у = -7; -0,9 х – 2у = 15 і т.д. 

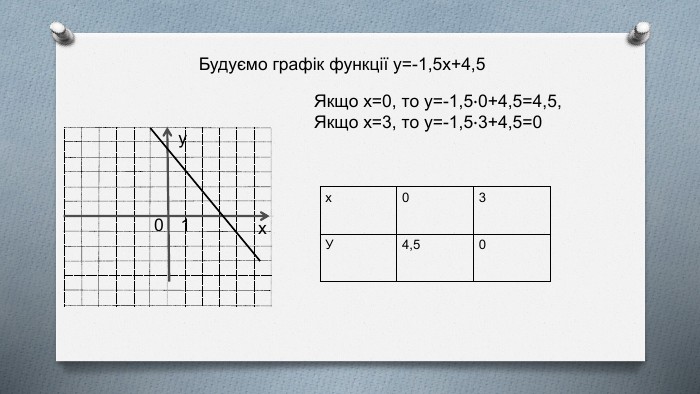
Розглянемо рівняння 3х+2у=9. Виразимо одну змінну через іншу, наприклад у через х. Перенесемо доданок 3х у праву частину, змінивши його знак на протилежний: 2у=-3х+9. Поділимо обидві частини одержаного рівняння на 2: у=-1,5х+4,5. Ми отримали формулу, яка задає лінійну функцію. Тому для побудови достатньо визначити координати двох будь-яких її точок.

Будуємо графік функції у=-1,5х+4,5{5940675 A-B579-460 E-94 D1-54222 C63 F5 DA}х03 У4,5001ух. Якщо х=0, то у=-1,5∙0+4,5=4,5,Якщо х=3, то у=-1,5∙3+4,5=0 

Алгоритм побудови графіка лінійного рівняння з двома змінними:1. Виразити змінну у через змінну х.2. Підібрати два значення змінної х.3. Обчислити відповідні значення змінної у.4. Позначити на координатній площині відповідні їм точки.5. Провести пряму через дві точки.

Наприклад. Побудувати графік рівняння 3𝑥+4𝑦=8. Виразимо з рівняння змінну у через змінну х: 𝑦=8−3𝑥4 Якщо 𝑥=0 , то 𝑦=8−3·04=2; якщо 𝑥=2 , то 𝑦=8−3·24=0,5. Позначимо в прямокутній системі координат точки (0; 2) і (2; 0,5) та проведемо через них пряму.  01ух{5940675 A-B579-460 E-94 D1-54222 C63 F5 DA}х02у20,5

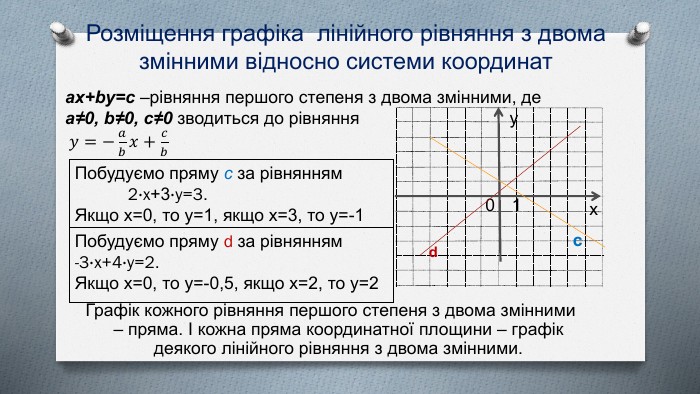
Розміщення графіка лінійного рівняння з двома змінними відносно системи координат Графік кожного рівняння першого степеня з двома змінними – пряма. І кожна пряма координатної площини – графік деякого лінійного рівняння з двома змінними.01ух{5940675 A-B579-460 E-94 D1-54222 C63 F5 DA}Побудуємо пряму c за рівнянням 2∙x+3∙y=3. Якщо х=0, то у=1, якщо х=3, то у=-1 Побудуємо пряму d за рівнянням -3∙x+4∙y=2. Якщо х=0, то у=-0,5, якщо х=2, то у=2{5940675 A-B579-460 E-94 D1-54222 C63 F5 DA}ax+by=c –рівняння першого степеня з двома змінними, де a≠0, b≠0, c≠0 зводиться до рівняння 𝑦=−𝑎𝑏𝑥+𝑐𝑏  сd

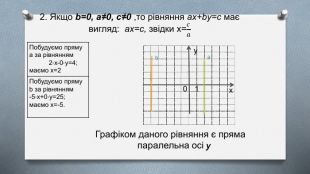
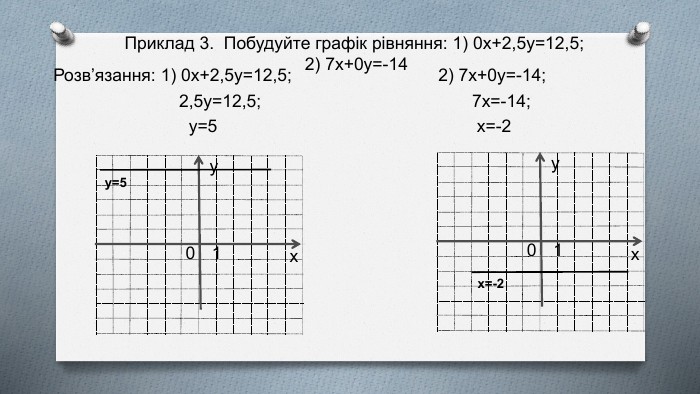
1. Якщо a=0, b≠0, c≠0 ,то рівняння ax+by=c має вигляд: by=c, звідки у = 𝑐𝑏 Графіком даного рівняння є пряма паралельна осі х{5940675 A-B579-460 E-94 D1-54222 C63 F5 DA}Побудуємо пряму a за рівнянням 0∙х+2∙у=4;маємо у = 2 Побудуємо пряму b за рівнянням 0∙х-2∙у=4;маємо у =- 2{5940675 A-B579-460 E-94 D1-54222 C63 F5 DA}baу=2у=-201ух

2. Якщо b=0, a≠0, c≠0 ,то рівняння ax+by=c має вигляд: ax=c, звідки x=𝑐𝑎 Графіком даного рівняння є пряма паралельна осі y01ухba{5940675 A-B579-460 E-94 D1-54222 C63 F5 DA}Побудуємо пряму a за рівнянням 2∙x-0∙y=4;маємо х=2 Побудуємо пряму b за рівнянням -5∙x+0∙y=25;маємо х=-5.{5940675 A-B579-460 E-94 D1-54222 C63 F5 DA}

3. Якщо с=0, a≠0, b≠0 , то рівняння ax+by=c має вигляд: ax+by=0, звідки y=- 𝑎𝑏𝑥 Графіком даного рівняння є пряма, що проходить через початок координат01ух{5940675 A-B579-460 E-94 D1-54222 C63 F5 DA}Побудуємо пряму a за рівнянням 3∙x-2∙y=0.y= 32х=1,5х. Побудуємо пряму b за рівнянням 2∙x+0,5∙y=0.y=- 4𝑥{5940675 A-B579-460 E-94 D1-54222 C63 F5 DA}ba

4. Якщо a=0, b=0, c=0 , то рівняння ax+by=c має вигляд: 0x+0y=0 Рівняння задовольняє будь-яка пара чисел. Графіком є вся координатна площина

5. Якщо a=0, b=0, c≠0 , то рівняння ax+by=c має вигляд: 0x+0y=с. Рівняння не має жодного розв'язку

Приклад 1. На якому з рисунків а-г зображено графік рівняння х+у=3 Розв’язання. Якщо у=0, то х+0=3; х=3. Якщо х=0, то 0+у=3. Отже, графік рівняння х+у=3 проходить через точки (3;0) і(0;3). Відповідь: в)

Приклад 2. Виразіть із даного рівняння змінну х через у і знайдіть які-небудь три розв’язки цього рівняння: 1) х+у=12; 2)х-7у=5; 3) 2х+8у=16. Розв’язання:1) х+у=12; х=12-у. Якщо у=1, то х=12-1=11,якщо у=10, то х=12-10=2, якщо у=12, то х=12-12=0. Отже, пари чисел (11;1), (2;10), (0;12) є розв’язками рівняння.2) х-7у=5; х=5+7у. Якщо у=0, то х=5, якщо у=1, то х=5+7=12, якщо у=-1, то х=5+7∙(-1)=-2. Отже пари чисел (5;0), (12;1), (-2;-1) є розв’язками рівняння.3) 2х+8у=16; (поділимо кожний член рівняння на 2), х+4у=8; х=8-4у. Якщо у=0, то х=8, якщо у=1, то х=8-4∙1=4, якщо у=2, то х=8-4∙2=0. Отже пари чисел (8;0), (4;1), (0;2) є розв’язками рівняння. 

Приклад 3. Побудуйте графік рівняння: 1) 0х+2,5у=12,5; 2) 7х+0у=-14 Розв’язання: 1) 0х+2,5у=12,5; 2,5у=12,5; у=5 2) 7х+0у=-14; 7х=-14; х=-201ух01уху=5х=-2

Приклад 4. Побудуйте графік функції 1) 0,5х+у=3; 2) 2(х+у)-3у=1. Розв’язання: 2)2(х+у)-3у=1; 2х+2у-3у=1; 2х-у=1. Розв’язання: 1)0,5х+у=3; 01ух{5940675 A-B579-460 E-94 D1-54222 C63 F5 DA}х02у-1301ух{5940675 A-B579-460 E-94 D1-54222 C63 F5 DA}х02у32

Приклад 5. При якому значенні а графік рівняння ах+4у=0 проходить через точку: 1)А(12;-4), 2)В(0;2); 3)О(0;0)Розв’язання: 1) Підставимо координати точки А(12;-4) у рівняння ах+4у=0:а∙12+4∙(-4)=0; 12а=16; а=43. 2) Підставимо координати точки В(0;2) у рівняння ах+4у=0:а∙0+4∙2=0; 0а=-8 Такого значення а не існує. 3) Підставимо координати точки О(0;0) у рівняння ах+4у=0:а∙0+4∙0=0; 0а=0, тобто при будь-якому значенні а. ∙ 

Приклад 6. Не виконуючи побудови, знайдіть координати точок перетину графіків рівнянь з осями координат: 1) х+7у=-21; 2) 5х-3у=15 Розв’язання. Якщо у=0, то х+7∙0=-21; х=-21. Отже, графік рівняння х+7у=-21 перетинає вісь х у точці (-21;0). Якщо х=0, то 0+7у=-21; у=-3. Отже, графік рівняння х+7у=-21 перетинає вісь у у точці (0;-3).2) Якщо у=0, то 5х-3∙0=15; 5х=15; х=3. Отже, графік рівняння 5х-3у=15 перетинає вісь х у точці (3;0). Якщо х=0, то 5∙0-3у=15; 3у=-15; у=-5. Отже, графік рівняння 5х-3у=15 перетинає вісь у у точці (0;-5).

Вправа «Третій зайвий» 1. Лінійним рівнянням з двома змінними є:1) 2) 3) 2. Яка точка належить графіку рівняння :1) А(2; 1);2) В(-2; 1);3) С(2,5; 2)3. Графіком якого рівняння є пряма паралельна осі х: 1) 2) 3)

4. Графіком якого рівняння є пряма, яка проходить через початок координат:1) 2) 3) 5. Графіком якого рівняння є пряма паралельна осі у:1) 2) 3)

До наступної зустрічі!

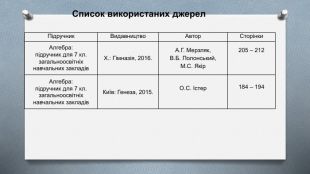
Список використаних джерел {5940675 A-B579-460 E-94 D1-54222 C63 F5 DA}Підручник. Видавництво. Автор. Сторінки. Алгебра: підручник для 7 кл. загальноосвітніх навчальних закладів Х.: Гімназія, 2016. А. Г. Мерзляк,В. Б. Полонський,М. С. Якір205 – 212 Алгебра: підручник для 7 кл. загальноосвітніх навчальних закладів Київ: Генеза, 2015. О. С. Істер184 – 194