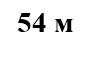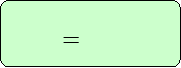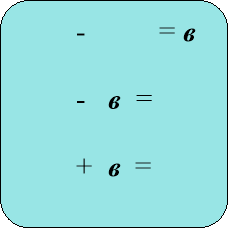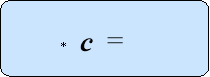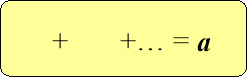Матеріали до уроків математики в 5 класі "Опорні блок-схеми з математики, 5 клас"
Відділ освіти
Новомосковської районної державної адміністрації
Попасненська ЗОШ І – ІІІ ступеня
Опорні
блок – схеми
з математики
для 5 класу
З досвіду роботи
вчителя математики
Попасненської
загальноосвітньої школи
І –ІІІ ступеня
Обідняк Марії Миколаївни
2020р.
Обідняк Марія Миколаївна
1953 року народження, учитель математики,
педагогічний стаж 47 років
освіта вища, вчитель вищої категорії,
старший учитель, відмінник освіти України.
«…Ідея «укрупнених блоків» - і в цьому переконує практика тих, що йдуть попереду – дозволяє учням в цілому сприйняти зміст теми, яку в подальшому будуть вивчати детально. Їх знання стають більш свідомими, глибокими. Виграє і теоретична, і практична сторона навчання.
П.М. Ерднієв, професор, доктор педагогічних наук, завідуючий кафедрою алгебри, геометрії і методики математики Калмицького університету
Передмова
Проблеми освіти і виховання, як і питання забезпечення людства продуктами харчування, енергією, збереження миру і оточуючого середовища відносяться в наш час до числа найзначніших глобальних проблем.
Освіта – це перш за все підготовка молоді до навчання протягом всього життя. Реалізація цієї ідеї передбачає, що будь-який громадянин, лише навчаючись на протязі всього життя, буде встигати за змінами, які будуть відбуваться в країні і в світі. Нова концепція навчання вимагає, щоб освіта мала відкритий характер, відкривала шляхи дальшого навчання. При цьому важливу роль грають чотири фактори. Шкільна освіта повинна:
- закладати систему знань, яка формується протягом життя;
- розвивати потреби і зацікавленість учнів, створювати позитивну мотивацію з метою подальшого навчання;
- сприяти виробленню умінь і навичок, необхідних при самостійному навчанні;
- прищеплювати інтерес до самоосвіти та самовиховання.
Визначні досягнення в усіх сферах економічного і суспільного розвитку невіддільні від науково-технічного прогресу, що грунтується на всебічному застосуванні природничих наук і насамперед математики. Як тут не згадати пророчі слова К.Маркса “Наука тільки тоді досягає досконалості, коли їй вдається користуватися математикою”.
Але оволодіти математикою неможливо, якщо узагальнення та систематизація математичних знань не буде невід’ємною частиною розумової діяльності, що лежить в основі встановлення взаємозв’язків між окремими деталями цілого, і наукового пізнання взагалі.
“Голова, наповнена окремими, беззв’язними знаннями, - писав К.Д.Ушинський, - схожа на комору, в якій все в безпорядку і де сам хазяїн нічого не знайде; голова, де тільки система без знань, схожа на крамницю, в якій на всіх ящиках є надписи, а в ящиках пусто”.
Виходячи з того, що в нинішніх умовах на уроках математики інформаційне навантаження на учня зростає, а час на вивчення предмета в загальноосвітній школі зменшено, спираючись лише на традиційні методи і форми роботи,бажаної мети в озброєнні учнів знаннями з математики досягти дуже важко. А значить, треба шукати методи, які б дозволили інтенсифікувати краще сприймання, застосування, систематизацію учнями знань, використовуючи властивості дитячої психіки, включаючи всі види пам’яті: словесно-логічну, образну, емоціональну.
Адже для того, щоб оперувати уявленнями і поняттями, слід зберігати їх в пам’яті. Особливу роль відіграє зорова пам’ять, недаремно ж говорять : “Краще один раз побачити, ніж сто раз почути”. Учням корисно при заучуванні не тільки повторювать, проговорюючи, текст, а й викликати в свідомості образи, сприйняті на уроці.
При відтворенні вивченого матеріалу дуже важливу роль грає пригаду-вання, яке потребує вольових зусиль. Полегшать процес пригадування асоціації та опори на пізнавання, а також багаторазове повторення.
Тому розв’язати питання інтенсифікації вивчення матеріалу намагаюсь за допомогою опорних блок-схем, які складала та вдосконалювала на протязі більше ніж 20 років, спираючись на передовий педагогічний досвід доктора педагогічних наук професора П. М. Ерднієва, вчителів В. Ф. Шаталова,
О.Г. Гайштута, В.П. Іржавцевої та інших, використовуючи основні положення педагогіки, дидактики та психології.
Запам’ятовування деталей буде міцнішим, коли ми сприймаємо образ в цілому. За словами професора П.М. Ерднієва “Укрупнена дидактична одиниця – це клітинка навчального процесу, яка складається із логічно різних елементів, що мають в той же час інфрмаційну спільність.Укрупнена дидактична одиниця має якості системності і цілісності, постійності до збереження на довгий час і швидкого проявлення в пам’яті.
…Фактором, що забезпечує високу якість укрупненого знання, може виступити загальний графічний образ, спільність символів для групи формул, наявність одних і тих же слів чи словосполучень…”
Взявши за основу цю ідею, до кожної теми навчального матеріалу в кож-ному класі, починаючи з п’ятого, було розроблено опорні блок-схеми. На цих блок-схемах наочно, детально та компактно подано матеріал, розрахований на сприймання учнів, показано всі причинно-наслідкові зв’язки між поняттями та умовиводами.
Перед вивченням кожної теми повідомляю мету її вивчення, які знання та навички учні повинні одержати під час її вивчення, де будуть застосовуватись ці знання, тобто проводжу щоденну мотивацію ближніх і дальніх перспектив. Завдяки опорній блок-схемі учні цілісно уявляють всю тему (розділ), яку потім вивчаємо по частинах. Цю блок-схему, намальовану на папері формату А-2, вивішую на дошці на протязі вивчення всієї теми (розділу). На першому ж уроці учні перекреслюють всі блок-схеми в спеціальний зошит, що ми називаємо опорним конспектом і який учні ведуть з 5 по 11 клас.
Матеріал кожного уроку викладаю традиційними методами, використо-вуючи підручник, наочність, дидактичний та роздатковий матеріал, ТЗН, моделі до кожної підтеми, застосовуючи нові технології навчання. При підве-денні підсумку поясненого матеріалу виділяю саме суттєве, показую його місце в загальній блок-схемі теми, що вивчається, розшифровую всі зображені опори (схеми, формули, зв’язки). Закріплення вивченого матеріалу йде на ос-нові опор відповідних блоків, на які звертаю увагу протягом всього уроку: при пояснені матеріалу, при розв’язуванні вправ та задач, при підведенні підсумків уроку, обов’язково наголошую на логічних зв’язках між записами. На кожному уроці після вивчення нової підтеми задіюються нові блоки даної схеми. Учні заповнюють відповідні блоки в своїх опорних конспектах записами, які є опорами для розуміння, запам’ятовування та швидкого відтворення вивченого матеріалу.
Кожен наступний урок починаємо з повторення всього вивченого матері-алу даної теми, а не лише матеріалу минулого уроку, обов’зково вказуючи на відповідний блок у схемі. Адже не даремно російська мудрість гласить: “Повторение – мать учения”. Для сильних учнів достатньо повторити 5-6 разів, щоб матеріал запам’ятався, а для слабких – 20 – 30 разів. Сприяє такому повторенню робота з відповідною опорною блок-схемою.
Таким чином, до кінця вивчення теми, завдяки багаторазовому повторенню матеріалу в учнів складається цілісна картина знань з даної теми.
При вивченні будь-якої теми з використанням опорних блок-схем в учнів задіюються всі види пам’яті:
образна – зорова (перед очима учнів весь час одна і та ж схема);
слухова (учні багато разів чують відповідні правила, теорми, алгоритми і т.д.) моторно-рухова (учні креслять, переписують схеми в опорні конспекти);
словесно-логічна (учні логічно пов’язують означення, правила, алгоритми, теореми з позначеннями в схемі) і емоціональна (діти одержують радість від того, що знають матеріал, це заохочує їх до роботи).
А це дає можливість краще та надовше запам’ятати матеріал теми, розділу, що вивчається.
Складаючи блок-схеми для вивчення подібних тем, навіть в різних класах, намагаюсь зберігати порядок розміщення блоків, заповнення їх кольором ( щоб кожен блок бачився окремо), використання однакових або подібних опор, щоб учням легше було сприймати, вивчати нове на основі раніше вивченого. (Наприклад, “Натуральні числа” і “Дії з натуральними числами” та “Десяткові дроби” у 5 класі; “Звичайні дроби” у 6 класі та “Раціональні дроби” у 8 класі; “Квадратний корінь” у 8 класі та “Корінь п –го степеня” у 10 класі).
Дуже важливо, що опорні блок-схеми, складені для тем, що вивчалися раніше, потім використовуються при вивченні матеріалу наступних тем, в яких треба використовувати раніше вивчений матеріал. Навіть не повторюючи матеріал по підручнику, діти швидко відтворюють потрібний матеріал за до-помогою відвовідної блок-схеми.
Так, наприклад, навіть в 10 -11 класах, де вивчаються тригонометричні, показникові, логарифмічні, диференційні рівняння, користуємось для повторення блок-схемами “Лінійні рівняння з однією змінною” ( 7 клас), “Квадратні рівняння” та “Дробово раціональні рівняння” ( 8 клас), а блок-схему “Схеми для розв’язування текстових задач за допомогою рівнянь” використовуємо з 5-го по 11 клас.
Використовуючи опорні блок-схеми, легко повторити матеріал за курс попереднього класу на початку навчального року, матеріал перед кожною тематичною контрольною роботою, наприкінці кожного семестру, при підсумковому повторенні в кінці навчального року та при підготовці до державної підсумкової атестації в 9 та 11 класах.
Отже, при вивченні математики за допомогою традиційної методики з одночасним застосуванням опорних блок-схем в учнів складається цілісне уявлення про вивчене, матеріал краще запам’ятовується і усвідомлюється, легше відтворюється при розв’язанні задач.
При такому вивченні матеріалу не порушується систематичність вивчення матеріалу учнями, які пропустили заняття, бо весь матеріал теми повністю повторюється на всіх наступних уроках, учень швидко включається в роботу разом з класом. Така методика роботи дає можливість всі знання привести в чітку і строгу систему, що в свою чергу, дозволяє вивчати матеріал глибше, детальніше, ефективніше; спонукає учнів повірити в свої сили.
Учні, що цікавляться математикою, мають можливість вивчати її глибше, виходячи за межі програми. Учні, які мають здібності до математики, але не використовували їх, з задоволенням працюють в класі і вдома. Слабкі учні набагато легше засвоюють необхідний мінімум знань, передбачений державними стандартами.
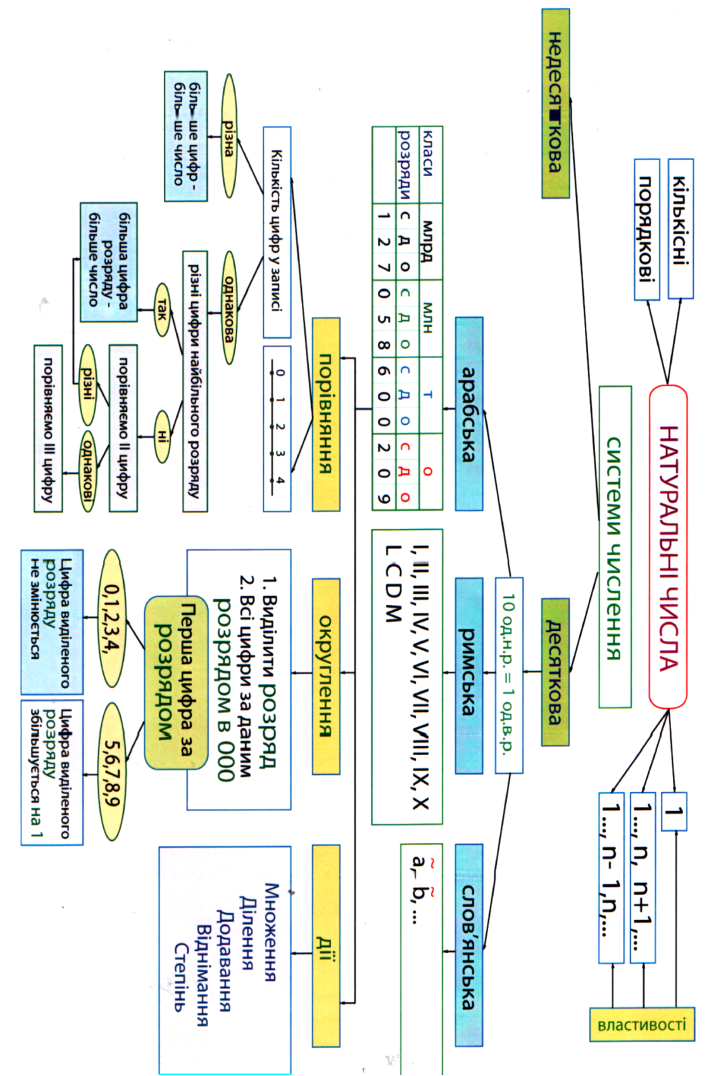
Блок-схема
«НАТУРАЛЬНІ ЧИСЛА»
Використовується при вивченні таких питань:
1. Означення натуральних чисел, ряд натуральних чисел
2. Види натуральних чисел.
3. Властивості натуральних чисел.
4. Позиційні системи числення – десяткові і недесяткові
5.Порівняння натуральних чисел
6. Округлення натуральних чисел до певного розряду
7.Ознайомлення з діями, що виконуються з натуральними числами.
Натуральні числа та дії над ними вивчають у початковій школі.
Учні початкової школи читають і записують багатоцифрові числа, що містять клас одиниць і клас тисяч. У V класі знання про натуральні числа поглиблю-ються і систематизуються.
Так, перший блок даної блок-схеми дає учням знання про те, що натуральні числа бувають кількісні та порядкові, а також висвітлює властивості ряду натуральних чисел.
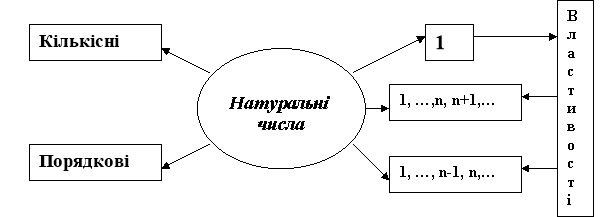1. Найменше натуральне число –це 1.
2. Кожне наступне число на 1 більше від попереднього.
3. Кожне попереднє число на 1 менше від наступного.
Основою вивчення теми «Натуральні числа» в 5класі, є теоретичні знання про позиційну десяткову систему числення.
Але поряд з цим вчитель може дати учням поняття і про інші позиційні системи числення, наголосивши, що ми користуємось арабським записом чисел. Тому при вивченні даної системи всю увагу учнів ми звертаємо на арабську десяткову систему числення.
Основним завданням вивчення зазначеної теми є розуміння суті позиційної системи числення, а саме:
1) для запису чисел використовують спеціальні значки (цифри); їх 10 ;
2) значення цифри залежить від місця (позиції), яку вона займає у записі числа;
3)10 одиниць нижчого розряду дають одну одиницю вищого розряду.
На основі вказаної блок-схеми формуються поняття клас, розряд, розрядні одиниці, розрядні доданки; формуються поняття мільйон, мільярд.
Особливо важливе значення надається розумінню учнями того, що :
1) кожен клас складається з трьох розрядів: одиниці, десятки, сотні;
2) щоб визначити кількість класів треба розбити число на класи по три цифри справа та визначити найвищий клас, найвищий розряд цього класу;
3) при читанні багатоцифрових чисел розряд будь-якого класу, позначений цифрою 0, пропускається (не читається);
4) при записі чисел пропущений розряд будь-якого класу позначається нулем.
Цей же блок наочно показує, скільки одиниць кожного розряду треба брати при записі числа у вигляді суми розрядних доданків:
257039=2·100000+5·10000+7·1000+0·100+3·10+9·1=200000+50000+7000++30+9
Блок «Порівняння» дає учням алгоритми практичного порівняння натуральних чисел з різною та однаковою кількістю цифр у записі.
Блок «Округлення» вказує на алгоритми округлення натуральних чисел до деякого розряду.
Цей блок використовується і при вивченні теми «Округлення десяткових дробів», адже частина завдань, запропонованих учням у даній темі, стосується саме до вміння округлювати натуральні числа до десятків, сотень, тисяч, мільйонів і т.д. Останній блок цієї схеми – «Дії» націлює учнів на те, які дії можна виконувати з натуральними числами.
Дії з натуральними числами
ІІ ступеня І ступеня
Блок - схема
« Дії з натуральними числами»
використовується при вивченні таких тем:
- Додавання. Властивості додавання.
- Віднімання. Властивості віднімання.
- Множення. Властивості множення.
- Ділення. Властивості ділення. Ділення з остачею.
- Порядок виконання дій при обчисленні значень числових виразів.
Дана блок-схема складається з 5 блоків, аналогічних за порядком розміщення матеріалу, що вивчається в даній темі. В кожному блоці розкри-вається суть кожної дії , що зображено в прямокутнику одного кольору. Знаходження невідомих компонентів для кожної дії зображено у прямокут-никах іншого кольору, властивості дій – ще іншого. Це дає можливість учням швидко знаходити потрібний матеріал у блок-схемі, бачити аналогію між матеріалом, що вивчається, про різні дії з натуральними числами.
При вивченні ділення особливу увагу загострюю на тому, що на 0 ділити не можна. Це зображено таким чином:
Частини блоків на знаходженні невідомих компонентів дають можливість краще вивчити правила знаходження невідомого компонента .
При цьому звертаю увагу учнів на аналогію при знаходженні невідомого доданка чи множника ( незалежно від того, на якому місці він стоїть) – виконанням протилежної дії, та від’ємника чи дільника і зменшуваного чи діленого.
Блоком « Порядок виконання дій» користуємось при розв’язуванні прикладів на всі дії як в п’ятому, так і в наступних класах. Засвоївши порядок дій з натуральними числами переносимо їх на дробові, раціональні числа, раціона-льні , ірраціональні , тригонометричні вирази в наступних класах.
Відповідні блоки з властивостями дій з натуральними числами використовуються також при повторенні матеріалу перед вивченням аналогічних властивостей дій з десятковими дробами в 5-ому класі, з звичайними дробами, з раціональними числами та виразами і т.д.
Так як вивчення всього курсу математики базується на розумінні дій з натуральними числами, то цей матеріал треба повторювати весь час, щоб знання та навички учнів дійшли до автоматизму.
Звичайні дроби
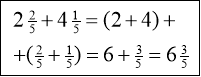
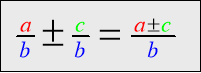
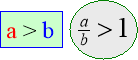
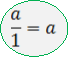
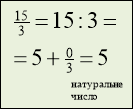
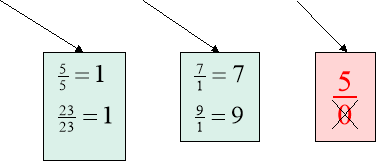
Блок - схема
« Звичайні дроби»
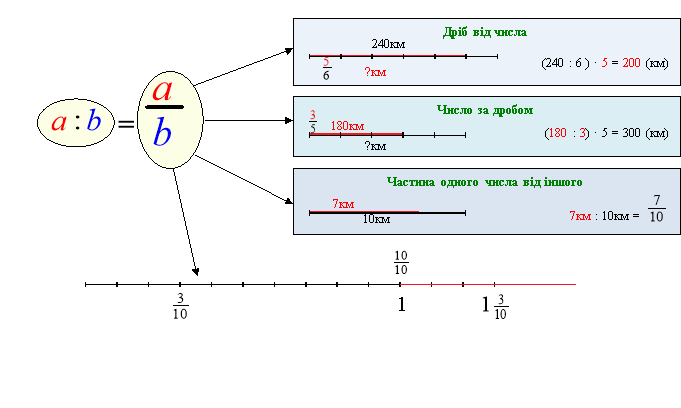
В блок-схему включено в порядку його вивчення весь матеріал курсу 5-го класу про звичайні дроби, застосування звичайних дробів для розв’язування трьох типів задач: знаходження дробу від числа, числа за його дробом та знаходження частини одного числа від іншого.
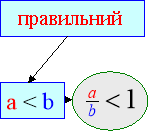
На координатному промені розміщені правильні та неправильні дроби.
Цей фрагмент дозволяє показати що правильні дроби менші за 1 , бо стоять зліва від неї, а неправильні – більші або дорівнюють 1.
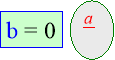
Блоки про правильні та неправильні дроби містять означення правильних та неправильних дробів, порівняння їх з 1, а також відомості про те, що неправильні дроби можуть мати знаменником будь яке натуральне число, крім 0, бо на 0 ділити не можна. Це допомагає учням краще усвідомити, що існує безліч способів запису числа 1 ( як неправильний дріб з однаковими чисельником і знаменником 5 /5 ; 23/23), та що будь-яке натуральне число можна записати у вигляді неправильного дробу із знаменником 1, або будь-яким іншим натуральним знаменником, що часто використовуватиметься в 6 класі при вивченні множення і ділення звичайних дробів. Наприклад: 7 = 7; 5 =15/3 .
Логічно поєднані між собою блоки перетворення неправильного дробу в мішане ( або натуральне) число і записом мішаного числа у вигляді неправильного дробу. Перед вивченням матеріалу про мішані числа необхідно повторити , використовуючи блок-схему «Дії з натуральними числами» блок « Ділення з остачею» .
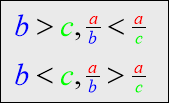
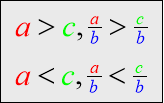
Блок «Порівняння» дозволяє запам’ятати правила про порівняння звичайних дробів з однаковими знаменниками ( які виділені синім кольором) та дробів з однаковими чисельниками ( виділеними червоним кольором).
Блок « Додавання і віднімання» дозволяє запам’ятати алгоритм до-давання та віднімання дробів з однаковими знаменниками, а також додавання і віднімання мішаних чисел.
Блок-схему “Звичайні дроби” можна використовувати для повторення матеріалу про звичайні дроби перед вивченням теми «Звичайні дроби» в 6 класі, а також при вивченні теми «Відсотки» в 5 класі, так як 1 % - це 1/100 частина числа, а п % - це п/100 частин, тому розв’язування задач на відсотки аналогічне до задач на звичайні дроби.
Десяткові дроби
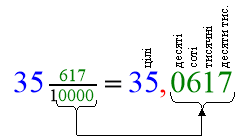
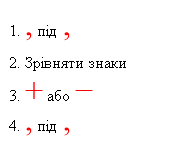
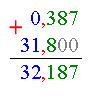
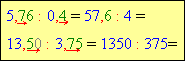
Блок - схема
« Десяткові дроби»
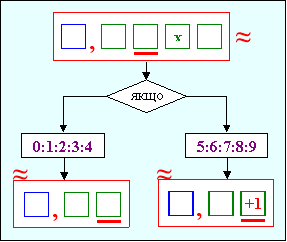
У першому блоці дається поняття десяткового дробу, запис звичайного дробу з знаменником , що дорівнює степеню числа 10 ( 10, 100,1000 т.д.) у вигляді десяткового дробу, пояснюється зв’язок запису та читання дробової частини( кількість цифр після коми) з кількістю 00 у знаменнику звичайного дробу, розміщення розрядів дробової частини на певному місці: десяті - на першому місці після коми, бо в знаменнику 10 – один 0, соті - на другому місці, бо в 100 - два 0 і т.д. Необхідно, щоб учні усвідомили, що на місці відсутнього розряду потрібно писати 0 ( як і в записі натуральних чисел).
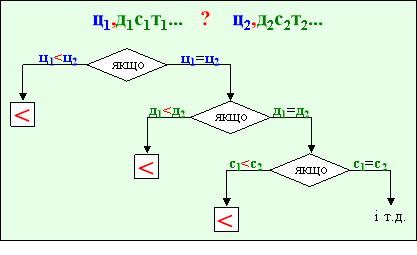
Блок « Порівняння» дає наочний алгоритм порівняння десяткових
дробів з різними та з однаковими цілими частинами.
Блок « Округлення» дає можливість зрозуміти, скільки цифр буде в записі числа при округленні його до певного розряду. Для цього під-креслюємо певний розряд і визначаємо наступну цифру за виділеним роз-рядом, а далі користуємося алгоритмом даного блоку.
Блок “ + і – “ наочно нагадує учням порозрядний принцип додавання і віднімання десяткових дробів, встановлює алгоритм виконання цих дій. Якщо учень неправильно виконує дії, необхідно домогтися, щоб учні чітко записували розрядні одиниці другого доданку ( чи від’ємника) під розрядними одиницями першого доданку ( чи зменшуваного) , а потім виконували дії як з натуральними числами, не забуваючи в результаті ставити кому під комою в доданках.
Блоки “Множення” і “Ділення” об’єднані між собою ( за принципом єдності протилежностей) діями множення та ділення десяткових дробів на розрядні одиниці 10, 100, 1000 і т.д. та 0,1; 0,01; 0,001 і т.д. Обов’язково слід постійно наголошувати на напрям руху коми - вправо чи вліво - на відпо- відну кількість знаків. Це полегшує засвоєння учнями правил та дозволяє усно виконувати багато вправ.
Перший фрагмент в блокові “ Множення” наочно показує, як підпи-сувати десяткові дроби при множенні «в стовпчик» та скільки знаків, почи-наючи справа, відокремити в результаті комою.
Слід звернути увагу учнів на те, що в проміжних результатах множення кома не ставиться ( це відповідає формуванню правила множення десяткових. дробів - перемножуємо їх як натуральні числа, не звертаючи уваги на кому).
Блок “Ділення” складає ться з двох фрагментів: ділення на натуральне
число та ділення на десятковий дріб.
При діленні на натуральне число самим важким для учнів є усвідомлення того, де ставить кому в частці. Перший фрагмент цього блоку направлений суто на цей момент, а весь інший процес відбувається як при діленні натуральних чисел.
Другий фрагмент блоку нагадує учням, що ділення на десятковий дріб зводиться до ділення на натуральне число. Тут застосовується основна властивість частки: якщо ділене і дільник помножити на одне і те саме число ( на 10, 100 і т.д. - кома вправо), то частка не змінюється.
Основні геометричні фігури
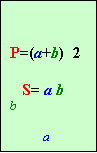
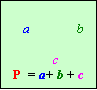
Блок - схема
«Основні геометричні фігури»
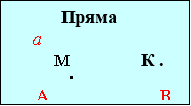
Перший фрагмент блок-схеми знайомить учнів з основними геометрич-ними поняттями: точка, лінія, пряма, площина.
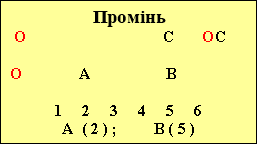
І хоч вивчення геометричного матеріалу в 5 класі починається з точки та відрізка ( за підручником “Математика 5” автори А.Г.Мерзляк., В.Б.Полон- ський, М.С.Якір), через кілька уроків ми прийдемо до висновку, що відрізок – це частинка прямої обмежена двома точками, що є кінцями відрізка. Аналогічно промінь - це частина прямої, обмеженої точкою лише з одного боку, яка називається початком променя.
Тобто, таке вивчення матеріалу про геометричні фігури є пропедевтикою вивчення геометрії в наступних класах.
В схемі чітко просліджується логічний зв’язок між блоками:
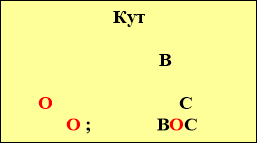
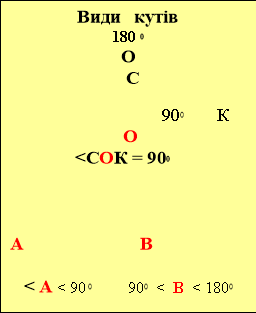
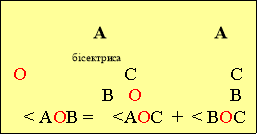
Промінь кут бісектриса кута види кутів
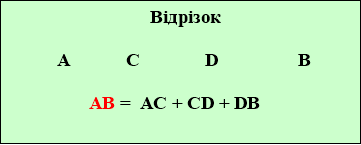
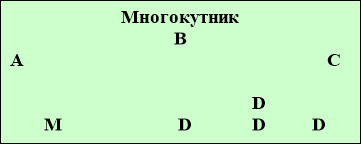
та пряма відрізок ламана многокутник
чотирикутник трикутник
( прямокутник квадрат) класифікація трикутників
( за сторонами, за кутами).
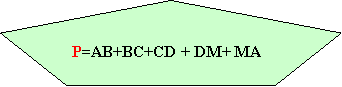
В кожному блоці даної схеми включено необхідні теоретичні положення для розв’язування задач ( довжина відрізка, довжина ламаної, периметри многокутника, прямокутника, квадрата, різних видів трикутників та площі прямокутника і квадрата).
Відсотки
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
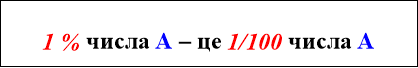
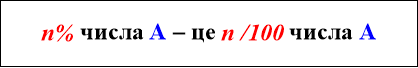
48 0,48 200 2 75 м 0,75
Блок – схема
«Відсотки»
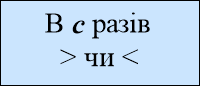
Ця блок-схема містить означення відсотка та типові задачі на відсотки. При початковому знайомстві з цією блок-схемою необхідно спів- ставити з блоком «Задачі на дроби» з блок-схеми « Звичайні дроби», адже
1 % - це 1/100 частина, а п % - це п / 100 .
Наприклад: При розв’язуванні задачі 1 можна запропонувати учням
аналогічну задачу з блок-схеми « Звичайні дроби». Вона допоможе їм
міркувати так: « 17% - це 17/100. Знаменник дробу (100) показує , що дане
число 48 треба розділити на 100 рівних частин, а чисельник (17) означає, що
таких частин треба взяти 17». Аналогічну роботу можна провести і при
розв’язуванні задач 2 і 3.
Блок - схема
«Знаходження невідомих компонентів»
Рекомендована вчителям 3-4 класів для кращого засвоєння назв компонентів при додаванні, відніманні, множенні та діленні, а також для вивчення алгоритмів знаходження невідомих компонентів( у підручниках початкової школи таких правил немає), використання їх для розв’язування рівнянь.
В 5-ому класі використовуються на уроках повторення матеріалу за курс початкової школи на початку навчального року , для розв’язування рівнянь при виченні теми « Додавання і віднімання звичайних дробів з однаковими знаменниками» , при знаходженні всіх невідомих компонентів в темі « Десяткові дроби» .
Всі блоки цієї схеми використовуються в 6-ому класі при розв’язуванні рівнянь, компонентами яких є натуральні числа, звичайн і дроби, десяткові дроби, раціональні числа.
Після вивчення властивості про перенесення доданків з однієї частини в іншу використовуємо 3 та 4 блоки даної схеми в 6-у і в наступних класах, якщо в цьому є потреба.
Знаходження невідомих
компонентів
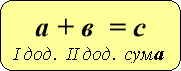
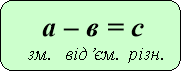
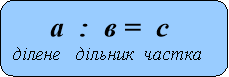
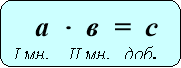
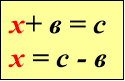
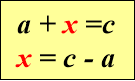
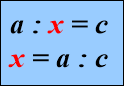
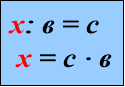
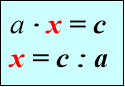
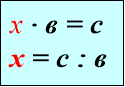
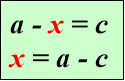
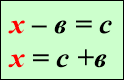
Блок – схема
«Схеми для складання рівнянь до текстових задач»
В даній блок-схемі є 4 схеми для складання рівнянь до основних 4-х типів задач, не включаючи задач на складання рівнянь за вказаним алгорит-мом. Користуючись підручником « Математика , 5 клас» ( автори А.Г.Мер-зляк, В.Б. Полонський, М.С.Якір, ) при розв’язуванні задач № 508-521 за допомогою рівнянь в 5-ому класі використовуються 1,3 та 4 схеми.
Після вивчення умови задачі необхідно записати її скорочений запис, проаналізувати її, встановити всі зв’язки між відомими та невідомими вели-чинами, визначити, яку невідому величину позначити через х , інші невідомі величини виразити через х ( використовуючи 1, 3, чи 4 схему) , а потім визна-чити, якою схемою треба користуватися для складання рівняння.
Креслимо цю схему на дошці ( а учні - в чорновиках)
+ + = ,
а потім вписуємо в кожен овал вираз, що відповідає кожній величині.
+ + =
+ + =
Тільки після цього складаємо рівняння: х +2х +3х = 120 або
х+ 2х + х+4 = 120.
Така попередня робота сприяє тому, що учні не загублять жодного виразу при складанні рівняння.
Цю ж блок-схему можна використовувати і у всіх інших класах при розв’язуванні текстових задач за допомогою рівнянь ( лінійних в 7-ому класі, квадратних та дробово-раціональних у 8 –ому та 9-ому класах) та системи рівнянь, як при вивченні теми, так і при повторенні матеріалу та підготовці до ДПА , ЗНО.
Л І Т Е Р А Т У Р А.
1. Програма Міністерства освіти і науки України «Математика,12-річна школа».
2. Бабанський Ю.К. « Інтенсифікація методів навчання». М.: Знание, 1987.
3. «Педагогіка» за редакцією Ю.К.Бабанського.М.: Просвещение, 1981.
- «Загальна психологія» за редакцією В.В.Богословського, М.: Просве-щение,1981.
- В.Оконь « Вступ до загальної дидактики» М.: Вища школа, 1990.
- Ерднієв П.М., Ерднієв Б.П. « Укруплення дидактичних одиниць при
навчанні математиці.» М.: Просвещение, 1986.
-
Фрідман Л.М. « Педагогічний досвід очима психолога» М.: Просвещение , 1987.
- Метельський Н.В. « Психолого-педагогічні основи дидактики матема-
тики»Мінськ, Вишейша школа, 1977.
9. Гайштут О.М. «Прийоми інтенсифікації навчання математиці в 4-5 класах» Київ. Радянська школа, 1980.
10. В.П.Іржавцева, Л.Я.Федченко « Систематизація і узагальнення знань учнів в процесі вивчення математики» К.: Радянська школа, 1988.
11. В.Ф.Шаталов « Точка опори» М.: Просвещение, 1985.
12. Слепкань З.І. « Психолого-педагогічні основи навчання математиці» К.: Радянська школа,1983.
Схеми для складання рівнянь до текстових задач
-
- більша величина
- менша величина
-
Дякую Вам за складені блок-схеми
про публікацію авторської розробки
Додати розробку