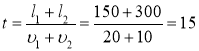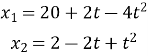Методична розробка "Розв'язання задач з теми: "Кінематика""
|
Методичний матеріал «Задачі з кінематики»
|
|
|
|
Мірошніченко Ганна Іванівна, викладач ВСП "Костянтинівський коледж ЛНАУ" |
|
|
Воронцова Олена Миколаївна, в.о. директора ВСП "Костянтинівський коледж ЛНАУ", викладач вищої категорії, учитель – методист, відмінник освіти України |
Приклади розв’язання задач
- Протягом якого часу швидкий поїзд довжиною 150 м, що йде зі швидкістю 72 км/год., буде проходити повз товарний потяг довжиною 300 м, що йде на зустріч зі швидкістю 36 км/год?
|
Дано: l1 = 150 м υ1 = 72 км/ч = 20 м/с l2=300 м υ2 = 36 км/ч = 10 м/с |
Розв’язок
Відповідь: 15 сек. |
|
t– ? |
-
М'яч впав з висоти
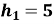 м, відскочив від підлоги і був зловлений на висоті
м, відскочив від підлоги і був зловлений на висоті 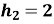 м. Чому дорівнює шлях
м. Чому дорівнює шлях 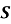 і модуль переміщення
і модуль переміщення 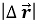 тіла?
тіла?
|
Дано:
|
Розв’язок
|
|
|
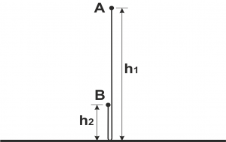
За визначенням, шлях — скалярна фізична величина, чисельно рівнадовжині траєкторії, тобто для знаходження шляху необхідно знайти відстань, пройдену тілом за час руху. Виходячи з цього визначення, наш шлях— це відстань від точки A до підлоги і відпідлоги до точки B (дивись рис.1):![]() (м).
(м).
За визначенням, переміщення – векторна фізична величина; вектор, що з'єднує початкову і кінцеву точку руху. Тобто для знаходження переміщення необхідно знайти модуль вектора переміщення (довжину цього вектора) і напрям цього вектора. У нашому випадку, це вектор, що з'єднує початок руху(точка А) і кінець руху (точка B). Намалюємо цей вектор (рис. 2).
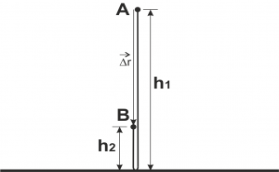
рис.2
В данному векторі нас цікавить його модуль, тобто довжина. З малюнка видно, що:![]() (м) .
(м) .
Відповідь: ![]() (м);
(м); ![]() (м) .
(м) .
-
Спортсмен на тренуванні пробіг
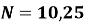 кіл радіусом
кіл радіусом 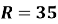 м кожен. Який шлях пробіг спортсмен? Чому дорівнює модуль його переміщення?
м кожен. Який шлях пробіг спортсмен? Чому дорівнює модуль його переміщення?
|
Дано:
|
Розв’язок
Траєкторія руху тіла — лінія, яку описує матеріальна точка, що рухається в просторі. Виходячи з умов завдання, тіло пройшло шлях, рівний заданому кількості довжин кіл (формула довжини кола: |
|
|
Для знаходження переміщення необхідно знайти модуль вектора переміщення (довжину цього вектора) і напрям цього вектора. Позначимо його на малюнку (рис. 1).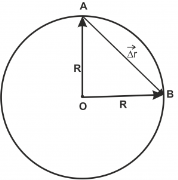 (рис.1) Переміщення
(рис.1) Переміщення
Виходячи з умов завдання, спортсмен пробіг 10 повних кіл і 0,25 частини кола. Нехай старт відбувся в точці А (вибираємо за власним бажанням, бо в задачі це не конкретизовано), тоді після 10 кіл спортсмен опинився в цій же точці, а після 0,25 кола (на ![]() кола) у точці В. Наразі ми бачимо, що наше завдання — знайти довжину
кола) у точці В. Наразі ми бачимо, що наше завдання — знайти довжину ![]() , на малюнку він є частиною прямокутного трикутника з катетами
, на малюнку він є частиною прямокутного трикутника з катетами ![]() та
та ![]() , і шуканої гіпотенузою
, і шуканої гіпотенузою ![]() .
.
Основним способом пошуку сторін прямокутного трикутника є теорема Піфагора, тому з ![]() :
:![]() (м).
(м).
Відповідь: ![]() (м);
(м); ![]() (м).
(м).
-
При бігу на марафонську дистанцію
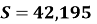 км результатом екстра класу є час
км результатом екстра класу є час 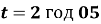 хв. Визначте середню швидкість бігуна.
хв. Визначте середню швидкість бігуна.
|
Дано:
|
Примітка.Час потрібно перевести в систему інтернациональности (СІ), тобто час в години: |
|
|
За визначенням, середньою швидкістю називається відношення всього шляху, яке пройшло тіло, до всього часу руху, тоді:![]() .
.![]() .
.
Відповідь: ![]() .
.
-
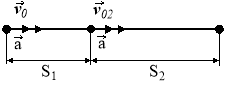
Автомобіль проходить першу третину шляху зі швидкістю
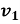 , а решту шляху – зі швидкістю
, а решту шляху – зі швидкістю 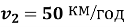 . Визначити швидкість на першій ділянці шляху, якщо середня швидкість на всьому шляху
. Визначити швидкість на першій ділянці шляху, якщо середня швидкість на всьому шляху .
.
|
Дано:
|
Розв’язок
Позначимо весь шлях через |
|
|
Очевидно, що: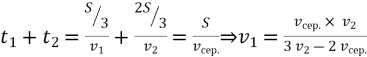 .
.
Отже,![]() .
.
Відповідь:![]() .
.
-
Рух матеріальних точок виражається рівнянням
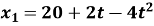 та
та 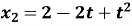 (довжина вимірюється в метрах, а час – в секундах). Швидкість даних точок будуть однаковими в момент якого часу?
(довжина вимірюється в метрах, а час – в секундах). Швидкість даних точок будуть однаковими в момент якого часу?
|
Дано:
|
Розв’язок
Знаходимо швидкість як першу похідну від переміщення: |
|
|
В момент часу ![]() швидкості точок будуть рівними, тобто
швидкості точок будуть рівними, тобто ![]() . звідси випливає, що
. звідси випливає, що ![]() (сек.) .
(сек.) .
Відповідь: ![]() сек.
сек.
-
Задано кінетичні рівняння довжини точки по колу:
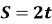 та
та 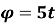 .
.
На якій відстані від вісі переміщення знаходиться віддалена точка?
|
Дано:
|
Розв’язок
Із рівняння |
|
|
Оскільки ![]() , то ми можемо виразити
, то ми можемо виразити ![]() .
.
Відповідь: ![]()
8. Тіло, що рухалося прямолінійно і рівноприскореному, пройшло за першу секунду 1 м, за другу - 2 м, яка його початкова швидкість?
|
Дано: t1=1 c l1=1м t=1с l2=2м |
Розв’язок: t2 = t1 + t = 2 c. Пройдений шлях при рівноприскореному русі
|
|
υ0 – ? |
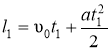 и
и 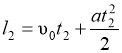 . Отсюда
. Отсюда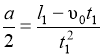 и
и  . Прирівнюючи праві частини рівнянь, отримаємо
. Прирівнюючи праві частини рівнянь, отримаємо
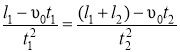 . Звідси
. Звідси 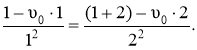 4 – 4υ0 =
4 – 4υ0 =
= 3–2υ0, 2υ0 = 1. υ0 = 0,5 м/с.
Відповідь: υ0 = 0,5 м/с.
Задачі для самостійного розв’язання
- Автомобіль рухається на повороті дороги, який являє собою чверть дуги кола радіуса 20 м. Визначте шлях і модуль переміщення автомобіля за час повороту.
-
Рибалка перепливає річку на човні, утримуючи його перпендикулярно до напрямку течії. Швидкість
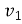 руху човна відносно води — 4
руху човна відносно води — 4  , швидкість
, швидкість 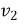 течії річки — 3
течії річки — 3  , ширина річки — 400
, ширина річки — 400 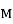 .
.
Визначте: 1) за який час ![]() човен перепливе річку та за який час
човен перепливе річку та за який час ![]() човен переплив би річку, якби не було течії; 2) модуль переміщення
човен переплив би річку, якби не було течії; 2) модуль переміщення ![]() і модуль швидкості
і модуль швидкості![]() руху човна відносно берега; 3) на якій відстані
руху човна відносно берега; 3) на якій відстані![]() униз за течією від вихідної точки човен досягне протилежного берега.
униз за течією від вихідної точки човен досягне протилежного берега.
-
Моторний човен рухається зі швидкістю
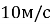 відносно води. Швидкість течії річки —
відносно води. Швидкість течії річки — 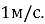 Визначте швидкість руху моторного човна відносно берега річки під час руху човна за течією; проти течії.
Визначте швидкість руху моторного човна відносно берега річки під час руху човна за течією; проти течії.
-
Крилата насінина набуває незмінної швидкості падіння
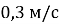 практично відразу після початку падіння з верхівки дерева. Наякій відстані від прикореневої частини стовбура впаде насінина, якщо швидкість вітру направлена горизонтально та дорівнює
практично відразу після початку падіння з верхівки дерева. Наякій відстані від прикореневої частини стовбура впаде насінина, якщо швидкість вітру направлена горизонтально та дорівнює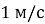 , а висота дерева становить
, а висота дерева становить 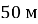 ? Яким є переміщення насінини відносно поверхні Землі?
? Яким є переміщення насінини відносно поверхні Землі?
-
Літак має долетіти до міста, розташованого на відстані
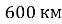 на північ. Із заходу дме вітер зі швидкістю
на північ. Із заходу дме вітер зі швидкістю 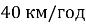 . Літак летить зі швидкістю
. Літак летить зі швидкістю 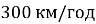 відносно повітря. Скільки часу триватиме рейс?
відносно повітря. Скільки часу триватиме рейс?
-
Перед відправленням потяга йшов дощ. Вітру не було, і краплі дощу падали вертикально. Коли потяг рушив, пасажири помітили, що дощ став косим, хоча погода залишалася безвітряною. Поясніть це явище. Визначте швидкість падіння крапель, якщо під час руху потяга зі швидкістю
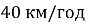 пасажирам здається, що краплі падають під кутом
пасажирам здається, що краплі падають під кутом 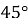 до вертикалі.
до вертикалі.
-
Рівняння проекції швидкості руху мотоцикла
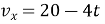 .
.
Визначте: 1) проекцію прискорення та початкову швидкість руху мотоцикла; 2) час, через який мотоцикл зупиниться.
-
Велосипедистка, щорухалася зі швидкістю
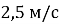 , починає розганятися і, рухаючись із прискоренням
, починає розганятися і, рухаючись із прискоренням 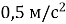 , сягає швидкості
, сягає швидкості 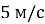 .
.
Знайти: 1) Яким є переміщення велосипедистки за час розгону?
2) Скільки часу розганялася велосипедистка?
3) Запишіть рівняння проекції швидкості руху та проекції переміщення.
4) Якою була швидкість руху велосипедистки через![]() після початку розгону? Через який інтервал часу швидкість її руху становила
після початку розгону? Через який інтервал часу швидкість її руху становила ![]() ?
?
5) Через який час після початку розгону велосипедистка подолає відстань ![]() , якщо рухатиметься з незмінним прискоренням?
, якщо рухатиметься з незмінним прискоренням?
-
Стрілу випустили з лука вертикально вгору зі швидкістю
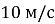 . Відомо, що через
. Відомо, що через 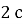 вона вже падала вниз із тією самою швидкістю. Визначте максимальну висоту польоту, шлях і переміщення стріли протягом цих
вона вже падала вниз із тією самою швидкістю. Визначте максимальну висоту польоту, шлях і переміщення стріли протягом цих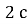 .
.
-
Із гелікоптера, який перебував на висоті
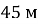 і рухався зі швидкістю
і рухався зі швидкістю 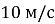 , упав невеликий важкий предмет. Через який інтервал часу предмет упаде на землю? Якою буде швидкість руху предмета в цей момент?
, упав невеликий важкий предмет. Через який інтервал часу предмет упаде на землю? Якою буде швидкість руху предмета в цей момент?
Розв’яжіть задачу для випадків, коли гелікоптер: 1) підніматься;
2) опускається; 3) рухається горизонтально.
-
Автомобіль рухається зі швидкістю
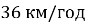 по опуклому мосту з радіусом кривизни
по опуклому мосту з радіусом кривизни 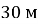 . Чому дорівнює і куди напрямлене прискорення руху автомобіля?
. Чому дорівнює і куди напрямлене прискорення руху автомобіля?
-
Точка на ободі колеса велосипеда рухається з прискоренням
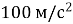 , радіус колеса —
, радіус колеса — 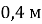 . З якою швидкістю рухається велосипед? Скільки обертів за хвилину здійснює колесо? Вважайте, що
. З якою швидкістю рухається велосипед? Скільки обертів за хвилину здійснює колесо? Вважайте, що  .
.
- Хвилинна стрілка годинника втричі довша за секундну. У скільки разів більше прискорення руху кінця секундної стрілки?
- З якою швидкістю має летіти літак над екватором Землі, щоб для людей у літаку Сонце не змінювало свого положення на небосхилі?
-
Дваелектрона рухаються в різні сторони зі швидкостями
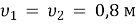 відносно нерухомого спостерігача. З якою швидкістю рухаються електрони відносно одне одного?
відносно нерухомого спостерігача. З якою швидкістю рухаються електрони відносно одне одного?
- Шкив діаметром 20 см робить 300 обертів за 3 хвилини. Визначити період обертання.
17). Тіло, рівномірно обертаючись навколо осі, робить 100 обертів за час 20 сек. На якій відстані від осі обертання знаходиться точка, яка рухається зі швидкістю ![]() ? Результат округлити до сотих.
? Результат округлити до сотих.
Довідник
-
Рівняння руху матеріальної точки
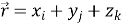
-
Вектор переміщення

-
Модуль вектора переміщення
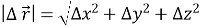
-
Прискорення
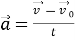
-
Модуль прискорення
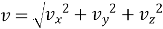
-
Повне прискорення при криволінійному русі

-
Нормальна складова прискорення
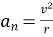
-
Переміщення
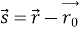
-
Рівняння координат
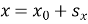 та
та 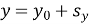
-
Швидкість рівномірного прямолінійного руху
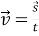
-
Кінетична рівняння рівномірного прямолінійного руху матеріальної точки вздовж осі Ох
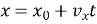
-
Закон додавання переміщень
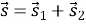
-
Закон додавання швидкостей
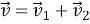
-
Кутова швидкість
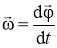 .
.
-
Кутове прискорення
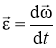
-
Період оберту
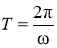 .
.
-
Частота обертання
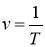 .
.
-
Циклічна частота обертання
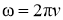 .
.
-
Дуже дякую. Професійно.
-


про публікацію авторської розробки
Додати розробку