Методичні рекомендації "Вивчення теми "Відсотки" у курсі математики 5, 6 класів"

Вивчення теми варто розпочати з презентації щодо застосування відсотків у реальному житті. Можна навести такі приклади:

1)

2) При кожній виплаті заробітної плати роботодавець повинен утримувати (відраховувати) по кожному працівнику наступні податки: податок на доходи фізичних осіб (ПДФО) 18% та військовий збір (ВЗ) 1,5%.

3) У державних будівельних нормах щодо містобудування (ДБН Б.2.2-12:2018 “Планування і забудова територій”), які діють з 1 вересня 2018 року та є обов’язковими, введений максимально допустимий відсоток забудови земельних ділянок при розміщенні нових житлових будинків. Він залежить від їх поверховості. Раніше в Україні будь-які обмеження поверховості житлової забудови були відсутні. Через це мікрорайони забудовувалися суцільно та хаотично по всьому периметру земельних ділянок. Про благоустрій прилеглої території, комфортні місця для прогулянок та відпочинку жителів тут не йшла мова. Тому у нових ДБН чітко прописано максимально допустимий відсоток забудови земельної ділянки в залежності від кількості поверхів. Чим вища поверховість, тим менший відсоток земельної ділянки відводиться на саму забудову і більший на облаштування прилеглої території, адже більша кількість жителів проживатиме в таких будинках. Згідно з ДБН при розміщенні на земельній ділянці одного або групи житлових будинків необхідно обов’язково дотримуватися розрахункових показників граничних параметрів забудови:

Якщо, наприклад, проєктується новий 11-поверховий житловий будинок, то максимально допустимий відсоток забудови земельної ділянки складає 30%, а інші 70% відводяться на облаштування зелених насаджень, зон відпочинку та дитячих майданчиків. Це сприятиме підвищенню комфорту проживання та якості життя людей та унеможливить суцільну забудову в містах.

3) Відсоток заряду акумулятора можна переглянути в рядку стану iPhone, iPad або iPod touch або в Центрі керування.

На iPhone X і новіших моделях відсоток заряду акумулятора можна переглянути в Центрі керування. Просто проведіть пальцем донизу від правого верхнього кута дісплея. На iPhone SE (2-го покоління), iPhone 8 і більш ранніх моделях, iPad і iPod touch (7-го покоління) відсоток заряду акумулятора можна переглянути в рядку стану. Перейдіть у меню «Параметри» > «Акумулятор» і ввімкніть функцію «Заряд у відсотках». У режимі енергозбереження на iPhone SE (2-го покоління) чи iPhone 8 або новіших моделях відсоток заряду акумулятора завжди показаний у рядку стану.

(без урахування окупованих територій (Криму, Севастополя, частини Донбасу)

Рівень безробіття — кількісний показник, який визначається як відношення кількості безробітних до загальної чисельності економічно активного працездатного населення країни (регіону, соціальної групи) та вимірюється у відсотках.

5) Прісна вода становить усього лише 3% від загальної кількості води на Землі. Решта – солона вода. Найсолоніше Мертве море, яке знаходиться на кордоні Ізраїлю та Йорданії. Відсоток солі у ньому досягає 35%. У воді Чорного моря міститься 1,8% солі.

               Чорне море                                                      Мертве море

Мотивації навчальної діяльності здобувачів освіти сприятиме ознайомлення їх з історією виникнення відсотків. Коротке інформаційне повідомлення може виглядати так.

Відсоткові розрахунки виникли ще в давнину у зв’язку з потребами комерційних операцій.

Перші "храмові" банки Вавилонії

Вавилон — стародавнє царство, яке розташовувалося на півдні сучасного Іраку. Саме там проводилися перші банківські операції. Як це відбувалося? Люди несли гроші та коштовності в храми в якості пожертвувань. І перед жерцями постала необхідність зберігати, примножувати накопичене. Вони вирішили вкладати гроші у вигідні підприємства. Також вони зрозуміли, що гроші із загального сховища можна давати людям на певний термін. Однак повернення відбувалося з відсотком за користування грошима. По суті, це були перші кредити. Згодом надання грошей населенню стало приносити жерцям найбільший дохід, у результаті чого і з'являється депозит — як інструмент залучення грошей із метою їх подальшого розміщення. Всі доходи йшли на облагороджування святинь, храмів. Таким чином, храми стали свого роду банками. Зокрема, Делоський, Дельфійський, Ефеський і Самоський храми. У них у підвалах були навіть обладнані сховища цінностей. Проіснував такий порядок досить довго — до XIV століття, коли більшість храмів були зруйновані та пограбовані. Перший у світі банк. У 1147-1148 роках у Генуї (нинішня Італія) було створено товариство, яке займалося збором деяких податків для забезпечення відсотків, погашенням позик і прийомом вкладів приватних осіб. У XV-XVII століттях дуже сильно вплинули на становлення капіталізму купецький і банкірський будинок Фуггерів у Німеччині. А в 1609-му році відкрився банк в Амстердамі. Трохи пізніше у 1694 році створено акціонерне товариство під назвою «Банк Англії». До речі, це був перший у сучасному розумінні емісійний банк, який відповідає за випуск паперових грошей. Пізніше відсотками почали послуговуватися, обчислюючи інші величини, які змінюються (зміна кількості населення, родючості землі та ін.).

У XIX ст. відсотки вже широко вживалися у статистиці та в інших науках, техніці, економіці, хімії, метеорології, сільському господарстві, у виробництві.

Нинішня ситуація.  У більшості країн банківська система складається з двох рівнів: комерційні банки — перший, нижній рівень (обслуговують фізичних та юридичних осіб із метою отримання прибутку); центральний банк — другий, вищий рівень. Здійснює емісійну та грошово-кредитну політику в країні, організовує міжбанківські розрахунки, систему рефінансування, координує роботу всієї банківської системи. В Україні це Національний банк України (НБУ).

Окремо варто сказати про системно-важливі банки. Це комерційні банки, які займають значну частку на загальному ринку, потенційний крах яких здатний привести до нестабільності фінансової системи держави. У 2021 році НБУ визначив Універсал банк, А-Банк, Альфа-банк, ОТП банк, Ощадбанк, Південний, Приватбанк, ПУМБ, Райффайзен Банк Аваль, ТАСкомбанк, Укргазбанк, Укрексімбанк і Укрсиббанк такими, які є системно-важливими для фінансової системи України.

Ввести поняття відсотків можна таким чином.

Соту частину будь-якої величини або числа називають відсотком (процентом). Слово «відсоток» замінюють знаком «%», тобто

1% = = 0,01

Наприклад: 1 коп. – один відсоток гривні, 1 см – один відсоток метра.

Слово «відсоток» («процент») походить від латинського слова per cent («на сотню»), що вказує зменшення одиниці виміру в 100 разів. Знак «%» прийшов, як вважають, від італійського слова cento («сто»), що у відсоткових розрахунках часто писалося скорочено cto. Звідси шляхом подальшого спрощення в скоропису літера t перетворилася на похилу риску (/) і виник сучасний символ для позначення відсотка.

Звертаю увагу, що на цьому етапі слід:

• формувати розуміння відсотків як частини будь-якого числа або числового значення величини (кілограм – це 1% центнера, ар – це 1% гектара);
• виробляти вміння:

• записувати відсотки у вигляді десяткового дробу;
• записувати у відсотках десяткові дроби;
• записувати звичайні дроби у вигляді десяткових, а потім у вигляді відсотків;

• вчити усно розв'язувати прикладні задачі:

1) З молока отримують 9% сиру. Скільки сиру можна отримати зі 100 кг молока?

2) Огірки містять у середньому 95% води.Скільки кілограмів води в 100 кг огірків?

3) Сплав містить 17% цинку. Скільки кілограмів цинку міститься в 100 кг сплаву? В 200 кг сплаву?

4) У домашній бібліотеці 700 книжок. Оленка прочитала за рік одну соту частину всіх цих книжок, а її брат Сергій – 1% усіх книжок домашньої бібліотеки. Порівняйте кількість книжок, які прочитали Оленка та Сергій.

5) Бригаді доручили відремонтувати ділянку дороги завдовжки 1200 м. Скільки метрів дороги бригада відремонтує, якщо виконає 1% завдання? 5% завдання? 70% завдання?

• дати можливість учням звикнути до введеного поняття, засвоїти іншу термінологію:

вся величина - це 100 %;

25 % величини – це 1/4 цієї величини;

половина деякої величини – це її 50 %;

30 % величини утричі більше, ніж її 10 %;

1/3 більше, ніж 25%;

4/9 деякої величини менше 50% цієї величини;

23% менше, ніж 1/4;

• використовувати геометричний матеріал (фронтальна робота, приклад завдання):

1) накресліть квадрат із стороною 10 см і поділіть його на 100 одиничних квадратів. Зафарбуйте:

а) 1% цих квадратів у зелений колір;

б) 7% цих квадратів у синій колір;

в) 15% цих квадратів у жовтий колір;

г) 21% цих квадратів у червоний колір;

2) яку частину прямокутника зафарбовано; знайдіть, скільки це становить відсотків (відповідь округліть до десятих).

Далі переходимо до розв'язування задач на знаходження відсотків від числа та числа за даним його відсотком. Автор підручника «Математика. 5клас» пропонує розв'язування задач двома способами. Методично доцільно спочатку знаходити один відсоток величини, а потім – кілька відсотків цієї величини.

Розглянемо задачу знаходження відсотків від заданого числа.

Задача. Площа поля становить 700 га. Пшеницею засіяли 67% поля. Скільки гектарів поля засіяли пшеницею?

Розв'язання. 1-ий спосіб. Знайдемо спочатку 1% від числа 700. Для цього треба 700 поділити на 100. Маємо 700 : 100 = 7. Отриманий результат треба помножити на кількість відсотків. Маємо 7 · 67 = 469 (га). Отже, пшеницею засіяно 469 га поля площею 700 га.

2-ий спосіб. Цей самий результат можна було отримати інакше: 67% = 0,67. Якщо виконати множення 700 на 0,67, то отримаємо

700 · 0,67 = 469 (га).

Отже, розв'язуючи першим способом, ми знайшли, скільки гектарів поля припадає на 1%, потім помножили цю кількість на відповідний відсоток. А розв'язуючи другим способом, виразили відсоток десятковим дробом і помножили дане число на цей дріб.

Розглянемо задачу знаходження числа за його відсотком.

Задача. З пшениці одержують 80% борошна. Скільки треба змолоти пшениці, щоб отримати 1200 кг борошна?

Розв'язання. 1-ий спосіб. Знайдемо, скільки кілограмів борошна припадає на 1%. Для цього треба 1200 поділити на 80. Маємо 1200 : 80 = 15. Щоб дізнатися, скільки пшениці треба змолоти, треба помножити 15 на 100 (оскільки вся пшениця становить 100%). Маємо 15 · 100 = 1500 (кг). Отже, треба змолоти 1500 кг пшениці.

2-ий спосіб. Цей самий результат можна було отримати інакше: 80% = 0,8. Якщо виконати ділення 1200 на 0,8, то отримаємо

1200 : 0,8 = 1500 (кг).

Отже, розв'язуючи першим способом, ми знайшли, скільки кілограмів борошна припадає на 1%, потім помножили цю кількість на 100. А розв'язуючи другим способом, виразили відсоток десятковим дробом і поділили дане число на цей дріб.

У 6 класі автори підручника пропонують більш складні задачі на відсоткові розрахунки, які можна розв'язувати за допомогою пропорцій. Розглянемо задачу на знаходження зміни відсотка за зміною числа.

Задача. У фермерському господарстві намолот пшениці  за перший день становив 50 т, а за другий день – 55 т. На скільки відсотків більше зібрали пшениці за другий день?

Розв'язання. За умовою задачі за перший день намолотили 50 т пшениці, що становить 100%. У задачі треба з'ясувати, на скільки відсотків 55 т пшениці більше за 50 т. Складемо короткий запис задачі:

І день: 50 т   –   100%

ІІ день: 55 т  –   (100 + х)%,

де х  –  кількість відсотків, на яку збільшилася маса пшениці. Складемо пропорцію:

Звідси 100 + х = , 100 + х = 110, х = 110 – 100, х = 10.

Отже, за другий день у фермерському господарстві зібрано пшениці на 10% більше.

Розв'язування задач – процес творчий. Його не завжди можна алгоритмізувати. Учнів треба вчити розв'язувати задачі, давати зразки: як аналізувати задачу, складати план, шукати спосіб її розв'язування (процес міркувань), оформляти розв'язання (логічну конструкцію).

Достатню увагу слід приділяти і задачам високого рівня складності, для яких треба проявити наполегливість і терпіння. Радість від розв'язування складної задачі –  нагорода для учнів. Розглянемо задачу 867 із зірочкою з підручника «Математика. 6 клас».

Задача. До просушування вологість зерна становила 23%, а після просушування 12%. На скільки відсотків зменшилася маса зерна після просушування? Колективне розв'язування задачі (після вивчення учнями умови) можна провести таким чином:

• Приймемо масу зерна до просушування за одиницю.

Скільки відсотків становить сухий залишок (суха маса) у зерні до просушування?

(100% – 23% = 77%)

• Яку частину займає сухий залишок у зерні до просушування? (0,77)
• Скільки відсотків становить сухий залишок у зерні після просушування?

(100% – 12% = 88%)

• Порівняйте маси сухих залишків у зерні до просушування та у зерні після просушування.

(Вони рівні)

• Яка ж  маса зерна після просушування?

(0,77 : 88% = 0,77 : 0,88 = = )

• Таким чином, ми прийняли масу зерна до просушування за 1 і знайшли, що маса зерна після просушування – 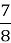. Складемо короткий запис:

1 – 100%

– (100 – х)%,

де х% – на стільки відсотків зменшилася маса зерна. Складіть пропорцію і розв'яжіть її

( =

Звідси

100 – х =7 100 : 8

100 – х = 87,5

х = 12,5

Отже, маса зерна після просушування зменшилася на 12,5%).

• Які види задач на відсотки застосовано у даній задачі? (знаходження числа за даним відсотком; знаходження зміни відсотка за зміною числа)

Під час вивчення теми «Відсотки» важливе значення має зацікавленість учнів у засвоєнні понять відсотків, відсоткових розрахунків. Задачі прикладного характеру виконують такі функції:

• допомагають учням зрозуміти зв'язок математики з повсякденним життям;
• готують здобувачів освіти до дорослого життя, у якому необхідність розрахунків (у тому числі відсотків) вимагається постійно.