Методичний посібник "Методика використання на уроках математики задач-“вкладок”"

Департамент освіти і науки

Полтавської обласної державної адміністрації

Відділ освіти Пирятинської міської ради Полтавської області

Пирятинський ліцей Пирятинської міської ради

Полтавської області

 

 

 

 

М.О.Філімонова

 

 

Методика використання на уроках математики задач-“вкладок”

 

(конспект уроку на тему

“Прямокутник. Площа прямокутника”, 5 клас)

 

 

 

Пирятин – 2017

Шкільна геометрична освіта передбачає пропедевтику систематичного курсу геометрії у процесі навчання математики у 5 – 6 класах. Саме у цей період в учнів формуються уявлення про основні геометричні фігури та їх властивості, уміння виконувати найпростіші вимірювання і побудови, розв'язувати задачі на обчислення значень геометричних величин (довжин, градусних мір кутів, площ, об'ємів). Тому понятійний апарат, графічні уміння і навички, отримані на цьому ступені вивчення курсу, мають стати міцним підґрунтям успішного вивчення геометрії в наступних класах. Таким чином, геометричний матеріал, призначений для вивчення у 5 – 6 класах, дозволяє з одного боку поглибити і розширити уявлення учнів про відомі їм геометричні фігури, а з іншого – має на меті підготувати школярів до вивчення систематичного курсу геометрії в 7 – 9 класах.

На мою думку, процес викладання геометричного матеріалу має специфічні риси:

1. Зміст курсу і методи його викладання мають опиратися на життєвий досвід і попередні знання школярів, причому основою курсу повинно бути максимальне використання наочності (моделі геометричних об’єктів, комп’ютерні презентації тощо).
2. Зміст курсу має бути логічно структурованим і органічно включатися в систему неперервної геометричної освіти.
3. Значна увага повинна приділятися формуванню усного і писемного мовлення учнів, їх грамотності.
4. Система вправ має бути спрямована з одного боку на розвиток просторової уяви та абстрактного мислення, а з іншого сприяти формуванню навичок виконання найпростіших логічних операцій.
5. Знайомство з новими поняттями, властивостями геометричних об’єктів має відбуватися на практичних роботах з елементами конструювання та вимірювальними роботами на місцевості.
6. Система вправ має включати значну частку прикладних задач, завдань на розвиток уміння бачити в навколишній дійсності геометричні фігури, здійснювати вимірювання “на око”.
7. Провідним методом вивчення геометричного матеріалу у                     5 – 6 класах є конкретно-індуктивний, проте з метою реалізації наступності вивчення геометрії в окремих випадках варто використовувати абстрактно-дедуктивний. Причому перехід від одного методу до іншого повинен здійснюватися виважено і доречно.

У курсі математики 5 – 6 класів вивчаються такі теми геометричного спрямування:

1. Пряма, промінь, відрізок, ламана. Кути

2. Многокутники. Площа прямокутника

3. Прямокутний паралелепіпед, куб, піраміда. Об’єм

Пропоную детальніше розглянути методи та прийоми вивчення теми “Прямокутник. Площа многокутника” з точки зору застосування методу математичного моделювання.

З поняттям “многокутник” учні знайомилися у процесі вивчення замкненої ламаної, тому основний акцент слід зробити на вивченні прямокутника (квадрата) і трикутника. Ці фігури образно відомі школярам ще з початкової школи. Однак заслуговують на увагу наступні моменти:

1.  При вивченні прямокутників, щоб відділити суттєві ознаки від несуттєвих, корисними будуть такі вправи: побудувати прямокутники з різним співвідношенням сторін та різним розміщенням; виготовити кілька моделей прямокутника з кольорового паперу, фанери тощо; знайти об’єкти у навколишньому середовищі, моделлю яких є прямокутник і т.д. Учні повинні засвоїти, що лише зміна градусної міри кутів порушує суттєві ознаки прямокутника. Аналогічні вправи слід пропонувати і при вивченні інших геометричних фігур, особливо коли мова ітиме про види трикутників.
2. Оскільки навичками знаходження периметру учні вже володіють, варто зупинитися на розв’язуванні практичних задач (наприклад, визначення довжини огорожі, розмірів пришкільної чи присадибної ділянки, футбольного поля тощо). Паралельно з цими мають бути завдання, в яких учням пропонується: вибрати масштаб і побудувати відповідне зображення (наприклад, розміщення кімнат власного будинку тощо); за даним периметром побудувати прямокутник (квадрат) і вказати кількість можливих побудов. Подібні завдання формуватимуть у школярів уміння співвідносити об’єкти навколишнього середовища з їх математичними еквівалентами, тобто будувати математичну модель.

Що стосується поняття “площа”, то її варто розглядати як величину, по відношенню до якої можуть бути встановлені критерії порівняння і яка має властивості схожі на властивості довжини. Однак процес знайомства учнів з поняттям “площа” має свою специфіку і здійснюється в кілька етапів:

1. введення поняття площі як величини;
2. знайомство з одиницями вимірювання;
3. вимірювання площ шляхом розбивання фігури на квадратні одиниці;
4. виведення правил обчислення площі;
5. розв’язування практичних задач.

Великі труднощі у школярів при розв’язуванні прикладних задач викликає процес заміни об’єктів, що описані в умові задачі, геометричними фігурами і термінами, оскільки для цього має бути гарно розвинене абстрактне мислення, що для 10 – 11-річних підлітків не є характерним. Тому на початкових етапах необхідно робити акцент на завданнях, в яких поряд з вихідним об’єктом зазначається його математичний еквівалент. Наприклад, математичним еквівалентом понять “цех”, “каністра” і т.д. є “прямокутний паралелепіпед”.

Задача 1. Приміщення цеху має форму прямокутного паралелепіпеда. Його довжина – 13 м, ширина – 12 м, а об’єм – 624 м3 . Обчисли його висоту.

Задача 2. Каністра має форму прямокутного паралелепіпеда, виміри якого 2, 3 і 4 дм. Скільки літрів бензину вміщується в ній? (1 л = 1 дм³)

Такі задачі сприяють формуванню і закріпленню в уяві дітей предметів, які мають і можуть мати форму прямокутного паралелепіпеда. Тому задачі, в яких немає прямого співставлення об’єкта і прямокутного паралелепіпеда (математичного еквівалента), в подальшому будуть розв’язуватися досить легко.

Також корисними будуть так звані задачі-“вкладки”, що передбачають побудову на базі однієї елементарної задачі системи завдань, розв’язання кожного з яких потребує залучення нових знань, активізації додаткових умінь та навичок. Наприклад, розглянемо таку задачу.

Задача 3. Класна кімната має розміри 5×8м. Знайдіть її площу.

Ця задача є елементарною, тому досить простими будуть для неї і математичні моделі (образна та знако-символьна), однак поставлені додаткові запитання дають змогу розкрити її прикладні можливості, збагатити і ускладнити модель. Зокрема:

1. Які ще лінійні розміри можуть бути у кімнати, яка рівновелика даній?
2. Чи існує в реальному житті кімната, один із лінійних розмірів якої дорівнює 1 м?
3. Як зміниться значення площі кімнати, якщо значення довжини кожної з її сторін збільшити удвічі?
4. Як зміняться значення лінійних розмірів кімнати, якщо значення її площі збільшити у 1,5 рази?

Запитання 1 – 2 формують в учнів розуміння реального походження даних, тобто дозволяють ситуацію, існуючу в математиці, перенести в реальну дійсність і з’ясувати її достовірність.

Запитання 3 – 4 сприяють засвоєнню структури формули для обчислення площі прямокутника.

Пропонуємо систему задач, створену на основі задачі 3.

Задача 4. Підлога класної кімнати має розміри 5×8м. Скільки банок фарби вагою 1 кг необхідно для фарбування підлоги, якщо витрати фарби на 1м² дорівнюють 120 г?

Задача 5. Якщо в кімнаті довжиною 8 м та шириною 5 м фарбувати нову підлогу, то технологія вимагає робити це тричі. Витрати для першого разу складають 150 г на м², для другого – 120 г на м², для третього – 70 г на м². Які загальні витрати фарби?

Після розв’язання цієї задачі варто задати учням кілька додаткових запитань типу:

1. Скільки банок фарби слід придбати, якщо вага однієї банки 0,75 кг?
2. Яку найменшу кількість банок фарби потрібно придбати, якщо в наявності є банки вагою 0,8 кг, 1,5 кг та 2 кг? 

Такі запитання сприятимуть різносторонньому аналізу ситуації і вибору можливих шляхів її вирішення.

Загалом задачі-“вкладки” яскраво демонструють процес ускладнення математичної моделі, сприяють удосконаленню навичок математичного моделювання та якісному формуванню в учнів загальнологічних прийомів розумової діяльності, хоча і вимагають від учителя додаткових зусиль та часу.

Пропоную один із варіантів проведення уроку формування умінь і навичок з теми “Прямокутник. Площа прямокутника” з використанням задач-“вкладок”.

 

 

 

 

 

 

 

 

 

 

 

 

Тема: Площа прямокутника

Мета: 

• формувати уміння і навички розв’язувати задачі практичного і логічного змісту, використовуючи формули площ;
• розвивати математичну мову учнів, логічне мислення, обчислювальні навички;
• виховувати культуру розумової праці, увагу, самостійність, активність, чесність.

Тип уроку: урок формування умінь і навичок

Обладнання:  підручник “Математика. 5 клас” А.Г.Мерзляк та ін.,  завдання для самостійної роботи, таблиця “Одиниці вимірювання площ”, комп’ютерна презентація “Площа прямокутника”, комп’ютерна презентація “Незакінчене речення”, комп’ютерна презентація “Фізкультхвилинка”.

Хід уроку

1. Організаційний момент

Учитель: Доброго дня! Сідайте. Розпочинаємо наш урок. Урок, щоб легко нам почати, слова важливі прошу пам’ятати:

• Будьте завзятими і не бійтеся помилитися.
• Міркуйте, творіть і дійте наполегливо.
• Мисліть активно, дійте оперативно.
• Продемонструйте свої кращі здібності.

 Успіху Вам!

2. Перевірка домашнього завдання

Учитель: На попередньому уроці ми ввели поняття площі прямокутника, встановили зв'язок між одиницями вимірювання площ. На сьогодні ви мали виконати №580 та №582

Вправа 580

1. 8 дм² = 800 см²; 16 дм² = 1 600 см²; 4 м² = 40 000 см²; 38 м² = 380 000 см²; 16 м ² 19 дм² = 161 900 см²; 74 м² 3 дм² = 740 300 см²
2. 340 000 м² = 34 га; 5 830 000 м² = 583 га; 53 км² = 5 300 га; 14 км² = 1 400 га;      5 км² 18 га = 518 га; 24 км² 6 га = 2 406 га.

Вправа 582

1. 48 а = 4 800 м²
2. 4 800 : 150 = 32 (м) – довжина поля
3. Р = 2×(32 + 150) = 364 (м)

Відповідь: периметр поля 364 

• Прошу консультантів дати інформацію про виконання домашнього завдання (учні – консультанти звітують про виконання домашнього завдання по рядах)
• Правильність виконання завдання ви можете звірити із розв’язанням на слайді.

Оголошення мети уроку

Учитель: Сьогодні на уроці ми продовжимо розв’язувати задачі на знаходження площ прямокутника, квадрата, а також покажемо застосування ваших знань на практиці, тому метою нашого уроку є:

 

 

 

 

 

 

 

 

 

Предмет математики настільки серйозний, що корисно не втрачати нагоди зробити його дещо цікавим (Блез Паскаль)

• Тому урок наш пройде незвично, а у цьому вам допоможе наш план.

 

 

 

 

 

 

 

 

 

 

3. Гра “Скарбничка знань” (Актуалізація опорних знань учнів)

Учитель: Повторення теоретичного матеріалу проведемо у вигляді гри “Скарбничка знань”, в якій ви даватимете відповіді на запитання:

• Що означає термін “ар”?   (Походить від латинського слова area - площа)
• Що в перекладі означає слово “гектар” ?   (Складається з двох слів гект (від грецьк . hekaton - сто) і ар 1га = 100а)
• Як зміниться площа квадрата, якщо кожну його сторону збільшити у 3 рази? (Збільшиться у 9 разів)
• Як зміниться сторона квадрата, якщо його площу зменшити у 25 разів? (Зменшиться у 5 разів)
• Як зміниться площа прямокутника, якщо одну сторону збільшити в 6 разів, а іншу – зменшити в 6 разів?  (Не зміниться)

4. Гра “Незакінчене речення” (Усне розв’язування вправ)

Учитель: Для подальшого розв’язування вправ і задач нам необхідно з’ясувати, чи добре ви знаєте, які властивості має площа і як обчислювати площу прямокутника і квадрата. Отже, закінчіть речення…

• Рівні фігури мають рівні…  площі
• Площа  фігури дорівнює… сумі площ її частин
• Площа прямокутника  із сторонами 11 см і 3 см дорівнює… 33
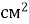
• Периметр квадрата площею 36 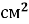дорівнює… 24 см
• Площа прямокутника дорівнює 56 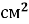. Знайдіть його ширину, якщо довжина дорівнює 8 см.  7см.

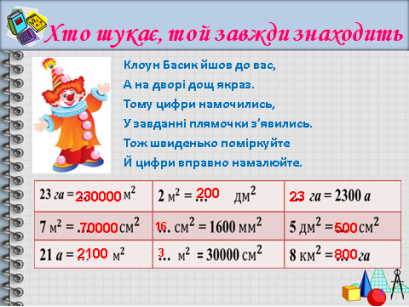5. “Хто шукає, той завжди знаходить”

 

 

 

 

 

 

 

 

 

 

6. “Знайди площу”  (Розв’язування задач)

Учитель: Розглянемо вправу 583. На малюнку зображено дві фігури. Потрібно знайти їх площу.

• Як знайти площу першої фігури?
• Якою властивістю ви скористалися?
• Запишіть розв’язання задачі у зошитах

(один із учнів записує розв’язання на дошці, а решта у зошитах)

1. 5*8 = 40 (см²) – площа першої фігури
2. 18*15 = 270 (см²) – площа другої фігури
3. 40+270 = 310 (см²) – площа заданої фігури

• Як знайти площу другої фігури?
• У чому відмінність?
• Зробіть висновки.

(учні записують розв’язання задачі на дошці і в зошитах)

1. 11*16= 176 (см²) – площа першої фігури
2. 11-8 = 3 (см) – ширина другої фігури
3. 3*6 = 18 (см²) – площа другої фігури
4. 18+176=194 (см²) – площа заданої фігури

7. “Фізкультхвилинка”

Учні встають з-за парт і повторюють рухи за зображенням на слайдах.

8. “Будівельно-ремонтна компанія” (Розв’язування задач практичного змісту)

Учитель: На даному етапі уроку наш клас перетворюється у будівельно – ремонтну компанію.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(40*120=4800 (г) = 4 кг 800 г)

 

(40*(150+120+70)=40*340=13 600 (г) = 13 кг 600 г)

9.  “Інтелектуальний марафон”

Для перевірки рівня засвоєння вами вивченого матеріалу проведемо самостійну роботу. (Учитель роздає завдання для самостійної роботи. Після написання самостійної роботи, учні обмінюються листками і за відповідями на дошці проводять взаємоперевірку, виставляють оцінки, а потім здають роботи учителю)

Варіант 1 1.Яку довжину має сторона квадрата площею 1 а? А. 1 дм.   Б. 1 м.   В. 10м.   Г. 100м. 2. Знайдіть площу прямокутника, якщо його сторони дорівнюють 2 см і 5 см. А. 7 .   Б. 14.   В. 20.   Г. 10. 3. Площа квадрата дорівнює 81. Чому дорівнює його сторона? А. 18 см.   Б. 9 см.   В. 8см.   Г. 10см. 4. Знайдіть периметр квадрата площею 49. А. 14 см.   Б. 28см.   В. 7 см.   Г. 12см. 5. Квадрат поділили на два рівні трикутники. чому дорівнює площа кожного з них, якщо периметр квадрата – 24 дм? А. 9 . Б. 288 . В. 18 . Г. 36 .

Варіант 2 1.Яку довжину має сторона квадрата площею 1 га? А. 1 км.   Б. 1 м.   В. 10м.   Г. 100м. 2. Знайдіть площу прямокутника, якщо його сторони дорівнюють 6 см і 7 см. А. 42 .   Б. 13.   В. 26.   Г. 84. 3. Площа квадрата дорівнює 25. Чому дорівнює його сторона? А. 52 см.   Б. 5 см.   В. 10см.   Г. 20см. 4. Знайдіть периметр квадрата площею 64. А. 16 см.   Б. 8см.   В. 32 см.   Г. 14см. 5. Квадрат поділили на два рівні трикутники. чому дорівнює площа кожного з них, якщо периметр квадрата – 16 дм? А. 32 . Б. 1288 . В. 8 . Г. 64 .

 

Варіант 1 В Г Б Б В

Варіант 2 Г А Б В В

10. “Домашнє завдання”

Повторити п. 21.

Виконати вправи  584, 586, 588

11. Підсумки уроку

Учитель підводить підсумок і виставляє оцінки

 

 

 

 

 

 

 

 

 

Учитель: Не достатньо опанувати премудрість, потрібно ще вміти нею користуватися. Отже, користуйтеся нею і йдіть вперед до знань цими трьома шляхами, які ми сьогодні відкрили для себе.