Математика – справді чарівна наука! Але, на жаль, далеко не всі школярі можуть це збагнути. Чому? З одного боку, все залежить від індивідуальної схильності дітей: комусь цікавіше малювання, а комусь історія. Але справа навіть не в цьому!
Часто у середніх і старших класах в межах шкільної програми математика сприймається як певна теорія, а для отримання правильного рішення необхідно виконувати ряд дій часто за єдиним алгоритмом. Тому в більшості школярів виникає сприйняття, що ця шкільна дисципліна зовсім не творча! Хоча, звісно, дуже багато залежить від учителя!
Пропонуємо 7 математичних трюків, узятих із книги А. Бенджаміна та М. Шермера «Магія чисел» і запозичених з японської методики, про які у шкільній програмі ані слова.
1. Множення на 9
Запропонуйте учням записати табличку множення чисел на 9. Зверніть їхню увагу на те, що існують цікаві закономірності, про які ані слова у шкільній програмі:
- При множенні послідовності від 1 до 9 на число 9, перші цифри в двозначних числах результатів зростають на 1, а другі цифри цього ж числа послідовно зменшуються на 1.
- Якщо записати поряд 2 стовпчики множення на 9 від 1 до 10 та від 10 до 1, то результати в кожному рядку двох стовпчиків будуть складатися з однакових цифр, які будуть стояти навпаки.
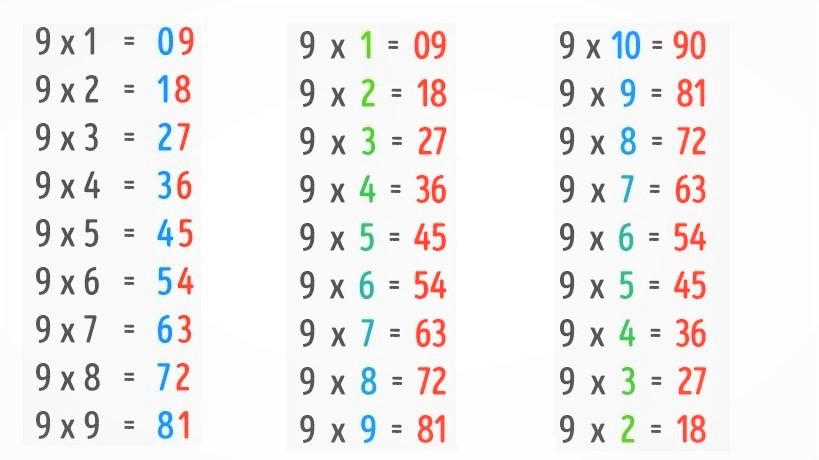
Лайфхак для школярів: як вивчити таблицю множення на 9:
Розглянемо на прикладі: обчислюємо 9х4. Для отримання двозначного числа результату, треба зменшити цифру 4 на 1 (4-1=3), а для отримання другої цифри – відняти від 10 саму цифру 4 (10-4=6). Результат –36.
Таким чином можна обчислити результат множення будь-якого однозначного числа на 9!
2. Множення за японським методом
Згідно з вимогами НУШ, таблиця множення в українських школах буде вивчатися лише з 4 класу. Але якщо спробувати опановувати множення за японським методом, то табличку вивчить навіть першокласник!
Приклад: Помножити 2 і 4
Згідно з математичною теорією, це означає, що необхідно обчислити 2+2+2+2=? або 4+4=?
У якості альтернативного способу можна скористатися графічним методом і обчислити кількість точок перетину відповідної кількості ліній.
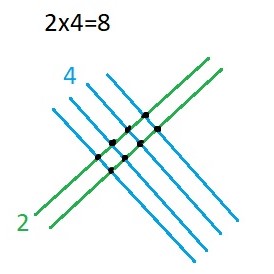
Таким чином можна множити і більш складні числа.
На малюнку нижче відповідним кольором позначені лінії, що відповідають певній цифрі, наведеній у прикладі.

Ций же спосіб можна використати і для більш складних обчислень, із якими, здавалося би, без калькулятора і не впоратися.
3. Додавання звичайних дробів із чисельником, який дорівнює 1
Після пояснення сенсу математичної теорії, покажіть учням прискорений варіант обчислення. Так, результатом додавання двох дробів є дріб, чисельник якого утворений сумою їхніх знаменників, а знаменник – множенням знаменників вихідних дробів.
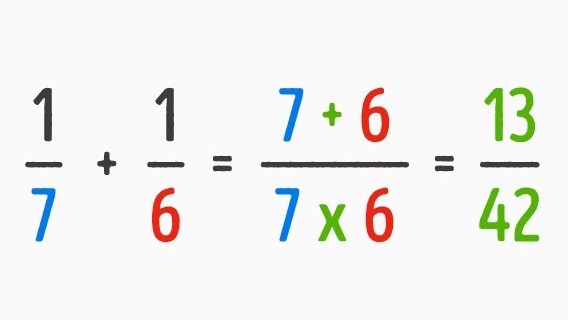
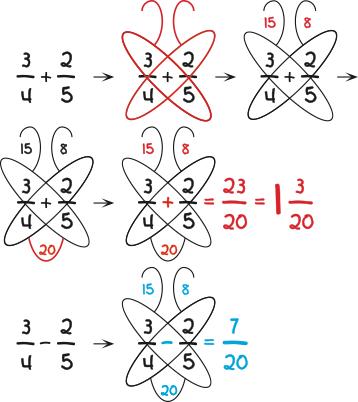
4. Метод «Метелик» для складання та віднімання дробів
Зазвичай вивчення дробів не викликає особливого захоплення у школярів. А спробуйте запропонувати вашим учням опанувати дроби за допомогою графічного прийому. Цей простий і швидкий спосіб не залишить школярів байдужими!
5. Множення будь-якого числа на 11
Здивуйте учнів та покажіть, як множення на 11 може бути простим та цікавим. Адже для цього достатньо виконати лише 1 дію, а не 2, як вивчається за шкільною програмою.
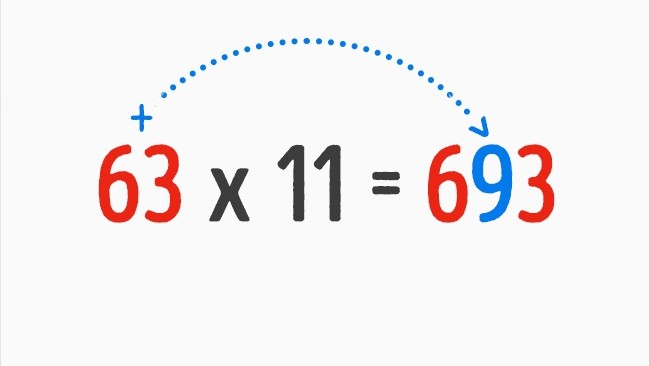
А як бути, якщо сума двох чисел складає 10 та більше? У такому випадку одиниці вписуємо поміж двома вихідними цифрами, а кількість десятків переносимо на наступний розряд.
Розглянемо на прикладі: 56х11 = 5(5+6=11)6 = 616.
А чи також легко помножити на 11 і більш складні числа? Так!
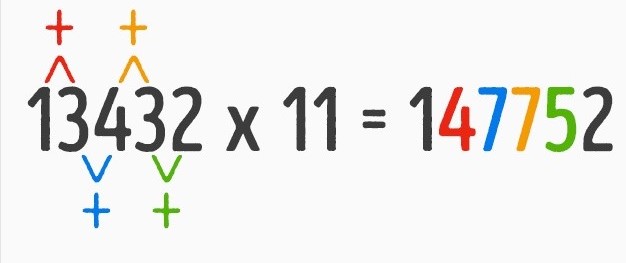
6. Множення двозначних чисел
Запропонуйте учням простий математичний приклад та запитайте, яким чином вони його пропонують вирішити. Щонайперше більшості спадає на думку метод стовпчика.
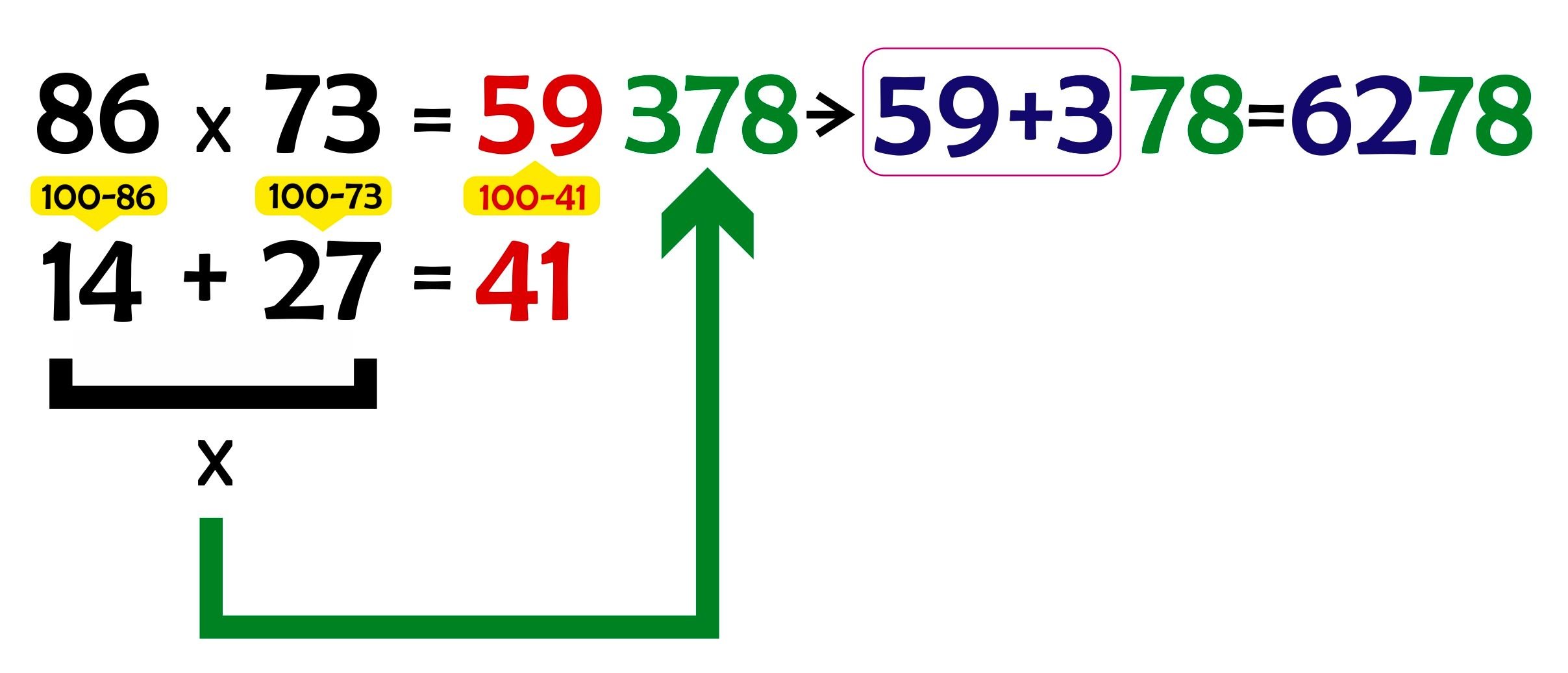
Доведіть учням, що множення двозначних чисел може бути швидким і цікавим!
Якщо приклад більш складний і друга група – не двох-, а трьохзначне число, тоді в отриманому п'ятизначному числі необхідно знайти суму двозначного числа і наступної цифри з трьох перших цифр.
7. Як легко обчислити відсоток від будь-якого числа
Як правило, для того, щоб обчислити відсоток від певного числа використовують метод пропорції. Його вивчають ще у молодшій школі, а згодом часто використовують у повсякденному житті. А як ще спростити цю математичну дію? Легко!
Приклад: знайти 40 % від 250.
Рішення:
Необхідно розділити обидва числа на 10.
40:10=4
250:10=25
2) Слід помножити отримані попередньо результати між собою:
4х25=100
Отже, 40% від 250 –100.
Математика – це легко і цікаво! Особливо, якщо дивитися на складні речі під правильним кутом, а краще – кількома!














Щоб залишити свій коментар, необхідно зареєструватись.