Позакласна робота з математики 5-6 класи

Передмова

    Сучасні потреби суспільства вимагають переходу на нову ,більш гнучку стратегію математичної освіти, ніж нинішня.

В умовах відтворення і зміцнення інтелектуального потенціалу нації, виходу науки і техніки в Україні на світовий рівень, інтеграції в світову систему освіти особливо важливим стає забезпечення належного рівня математичної підготовки підростаючого покоління. Це пов’язано з тим, що математика має великі можливості для розвитку логічного мислення, просторових уявлень і уяви, вміння моделювати ситуації.

     Першочерговим завданням, яке постає перед вчителями математики - розвиток логічного мислення учнів, основної складової при підготовці учнів до майбутньої трудової діяльності. Ким би не старався стати учень в майбутньому - йому треба вміти правильно і швидко міркувати, діяти організовано, враховуючи обставини і наявні ресурси.

      В останні роки зріс інтерес до математичної логіки - напряму сучасної математики, який швидко розвивається і широко застосовується.

       Природно виникає потреба у збірнику задач логічного характеру. Пропонований посібник і є спробою створити такий збірник. В ньому підібрані досить різноманітні вправи, які охоплюють різні форми задач логічного змісту.

       Посібник допоможе юним  любителям математики цікаво і корисно використати свій вільний час, а вчителі математики знайдуть  матеріал  для позакласної роботи, для проведення математичних гуртків у 5-6 класах, для підготовки учнів до участі в математичних олімпіадах.

       В посібнику наведена орієнтовна програма математичного гуртка для  учнів 5-6 класів та завдання, з вказаними відповідями і вказівками , щодо розв’язання  задач, відповідно до розділів програми.

 

 

 

 

Орієнтовна програма математичного гуртка

для учнів 5-6 класів

           Мета гуртка - розвивати логічне, творче мислення учнів 5-6 класів загальноосвітніх шкіл.

           Програма побудована з урахуванням  принципів математичної освіти:

 - бути цілісною системою формування особистості на основі досягнень математики;

 - бути безперервною і забезпечувати наступність у навчанні математики;

 - ґрунтуватись на засадах гуманізації навчально – виховного процесу;

 - на різних ступенях навчання здійснювати рівневу  і профільну диференціацію навчально – виховного процесу на основі базового змісту математичної освіти; 

 - навчання математики повинно мати розвиваючий характер і прикладну спрямованість; сприяти розвитку інтелекту, алгоритмічної культури, математичної інтуїції, вміння і бажання вчитися, застосовувати свої знання для розв’язання практичних і прикладних задач;

   - в організації навчального процесу доцільно надавати переваги методам активного навчання і його сучасним технологіям.

Провідну роль у здійсненні поставлених завдань відіграє вчитель математики.

Від його математичної, психолого – педагогічної та методичної підготовки, особистих якостей залежить підготовка конкурентно – спроможного, компетентного випускника школи, відповідно до рівня сучасних вимог.

 

 

 

 

 

 

 

 

 

5 – 6 класи

(1 год. на тиждень)

№	Зміст навчального матеріалу	Всього годин
1	Математичні ребуси	5
2	Логічні задачі математичного змісту	5
3	Площа знайома і несподівана	3
4	Математика шахової дошки	5
5	Лабіринти	4
6	Задачі на зважування, переливання, пересипання, перекладання	4
7	Логічні задачі	5
8	Математичні ігри	4
		35

   Основні вимоги до знань і вмінь учнів на кінець навчального року.

Учні повинні знати і розуміти:

  - поняття: «ребус», «кросворд», «математичний фокус», «лабіринт»;

  - правила математичних ігор: «морський бій», «стомахіон», «танграм»;

  - правила гри на шаховій дошці;

  - алгоритм розв’язування задач на зважування, перекладання;

  - поняття : «рівновеликий» і «рівно складений».

Учні повинні вміти:

  - читати математичні ребуси, кросворди;

  - розв’язувати нестандарті задачі логічного характеру на рух, на спільну роботу;

   - ходити лабіринтами геометричних фігур;

- розв’язувати задачі на розрізання і перекладання фігур;

 

 

 

І. МАТЕМАТИЧНІ РЕБУСИ

 

ВСТУП

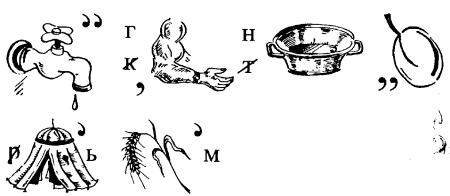
Ребус - це особлива задача, в якій текст подано зображенням предметів, цифрами, буквами, нотами.

Якщо частина зашифрованого слова співпадає з назвою предметів, то в ребусі вони зображаються малюнком, який відтворює ці предмети.

Подамо правила читання ребусів.

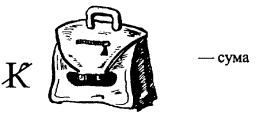
1) Якщо одна або більше ком поставлені перед зображенням предмета (предметів), то це означає, що від назви предмета (предметів) потрібно відкинути відповідну кількість букв зліва.

 

Щоб прочитати цей ребус, потрібно до слова "сто", зображеного цифрами 1 і 0, приєднати назву птаха "ворона", відкинувши перші дві букви — "в, о" - зліва. Читаємо ребус: сторона ( сто- /во/ -рона).

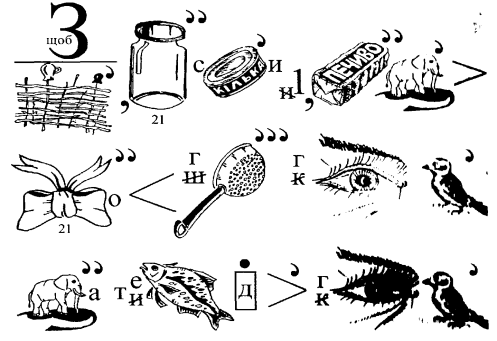
2) Якщо одна або більше ком поставлені після малюнка предмета (предметів), то це означає, що від назви предмета або предметів потрібно відкинути одну або більше букв справа.

 

 

 

 

 

В слові "чиж" відкидається перша буква справа /ж/, в слові "слон" - /н/. Отримаємо слово "число" (чи- /ж/ -сло /н/). Другий ребус читаємо: один (о- дин /я/).

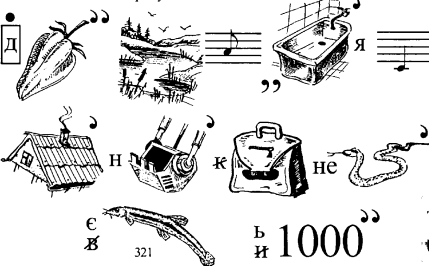
3) В деяких випадках в ребусі вказується, яку букву треба відкинути в середині слова. В розгадці ребуса вона опускається.

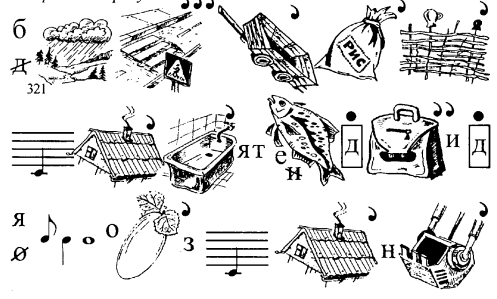
4) Інколи букву, яка міститься в слові, замінюють іншою. Наведемо приклад ребуса такої структури

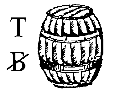
В цьому ребусі буква "б" в слові "бочка" перекреслена і замінюється буквою "т". Читається ребус "точка".

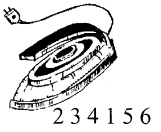
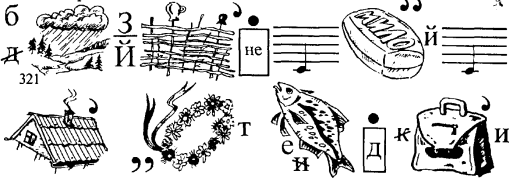
5) Суть наступного шифрування ребуса полягає в тому, що числа, записані під малюнком (інколи словом), показують місце тією чи іншої букви в зашифрованій частині ребуса.

На малюнку зображено силача. Під малюнком записані числа 3,2,4, 5 і 1. В розгадці ребуса букві "ч" відводиться перше місце, букві "й" • — друге, букві "с" — третє, букві "л" — четверте, букві "а" - п'яте. Читається ребус — "числа".

6) Якщо ж при попередньому способі відгадування ребуса деяка буква замінена іншою, то зашифрована частина ребуса подається, наприклад, так:

 

В ньому буквам п, р, а, с, к, а відповідно надане місце: 1,2,3, 4, 5, 6-е. В розгадці ребуса буква "с" має перше місце, "п" друге, "р" - — третє, "а" - — четверте, "к" - - п'яте (перед малюнком праски буква "к" перекреслена і замінена буквою "в"), "а" шосте. Отримуємо слово "справа".

7) В тому випадку, коли буква (букви) не входять в розгадку ребуса і відповідні їм порядкові номери (числа) перекреслені, то їм надаються останні місця.

В цьому ребусі першою записана буква "г". Місце цієї букви зберігається в розгадці ребуса. На другому місці слова "гора" записана буква "о", яка в розгадку ребуса не входить, тому їй в розгадці надано останнє, четверте, місце і ця цифра перекреслена. На третьому місці стоїть буква "р", але в розгадку ребуса вона входить і надаємо їй друге місце. На четвертому місці слова "гора" стоїть літера "а", їй надаємо третє місце в ребусі. Отримуємо слово "гра" і добавляємо букву "м". В результаті виходить, що слово "грам" (одиниця маси) — розгадка ребуса.

Інший варіант цього правила подамо на прикладі ребуса:

 

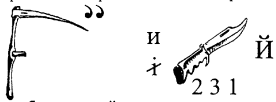
Розгадка ребуса: кожний.

8) При розв'язуванні ребуса, в якому буква (цифра) або сукупність букв (цифр) зображено в іншій букві, в текст розгадки ребуса вводиться буква "в" або "у".

 

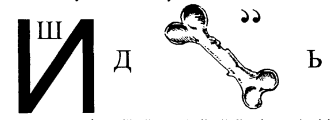
Розгадка: швидкість ("ш" - в - "й" - "д" -кістка /ка/ь).

9) На відміну від попереднього принципу розгадування ребу­са, цей здійснюється так: спочатку називається буква "в" або "у", потім букви, в яких зображені інші знаки, і на кінець — букви (слова і т.д.), які зображені всередині попередніх знаків.

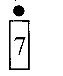- "в" - "і" - "сім". Розгадка ребуса — вісім

 

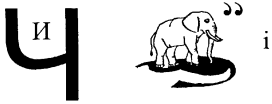
"в" - "ч" - "и" "слі". Розгадка ребуса — в числі

10) Коли в ребусі за одними знаками містяться інші, то спочатку називаємо склад "за", потім слово або сукупність слів, які стоять спереду, і в кінці те слово або сукупність слів, які записані на задньому плані.

 

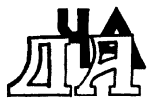за "да" - "ча". Розгадка ребуса—задача

 

11) Слова в ребусі можуть бути подані і таким розміщенням частини слів, як "перед".

Наведемо приклад такого ребуса

 

Відгадка ребуса: число передує (чи -сло перед - у - є).

12) Ребус можна задати дробом. Спочатку читається слово, записане над рискою, потім - прийменник "на", і в кінці - слово під рискою.

. В цьому випадку слово "десять" замінено словом "дцять" (десять). Читаємо ребус: дванадцять (два - на - дцять).

 

 

 

 

 

 

 

 

 

 

 

 

 

1.1.  ДОДАВАННЯ

1. Відгадайте ребуси. 

                                                                                                               

 

 

 

2. Прочитайте ребус

 

 

3. Відгадайте ребус

 

4. Прочитайте ребус

 

 

 

5. Прочитайте ребус

 

 

 

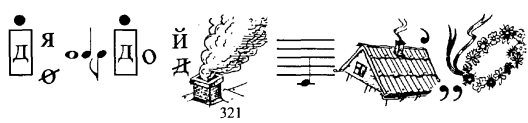
6. Прочитайте правило порядку виконання дій.

 

 

 

 

 

 

 

 

 

 

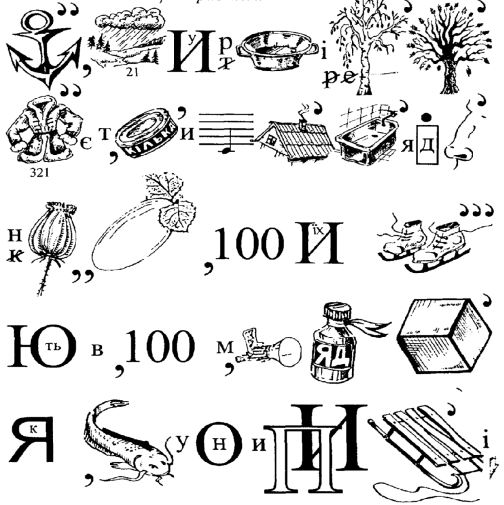
7. Прочитайте ребус

 

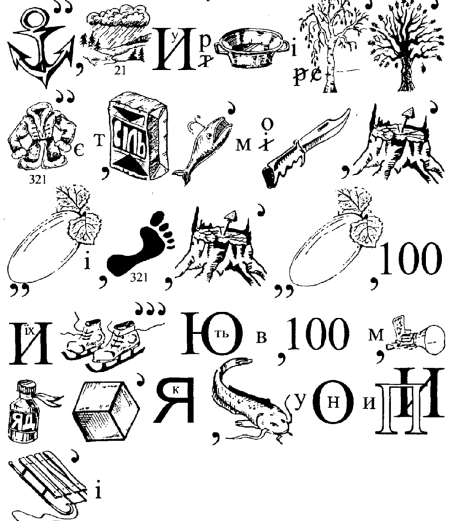
8. Відгадайте ребус

 

 

 

2.        ВІДНІМАННЯ

9. Прочитайте назви чисел при дії віднімання

 

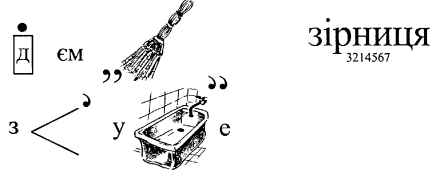
10. Прочитайте ребус

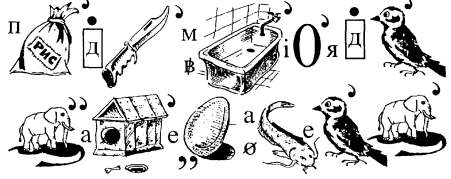
11. Прочитати правило, зашифроване ребусом

 

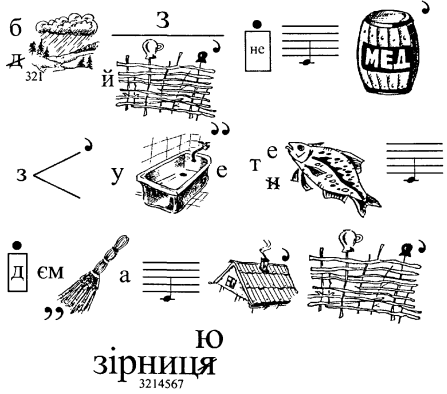
12. Відгадайте ребус

 

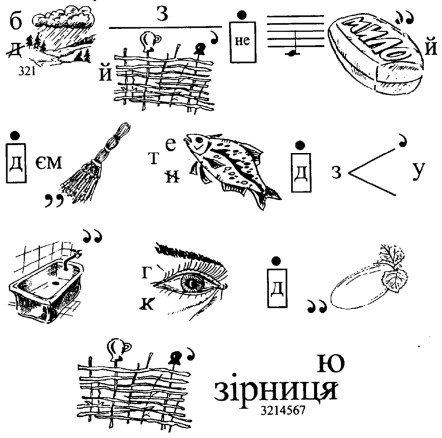
3.        МНОЖЕННЯ

 

13. Прочитайте ці слова

 

 

 

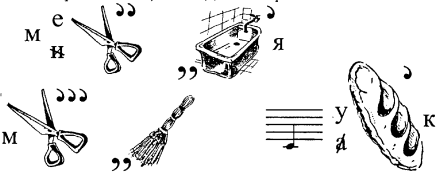
14. Про яку дію говориться в ребусі

 

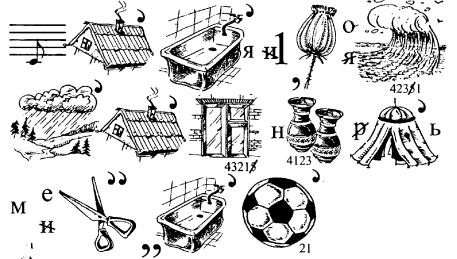
15. Прочитайте правило, яке записане ребусом

 

 

 

 

 

 

 

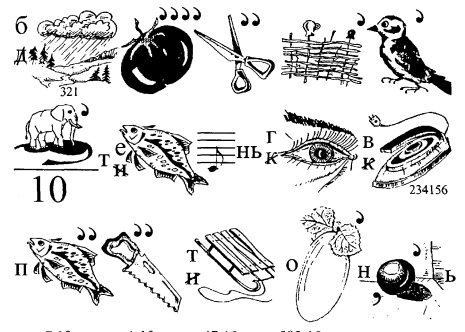
16. Прочитайте ребус

17. Розгадайте ребус

 

 

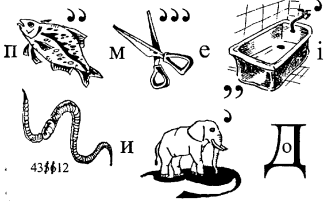
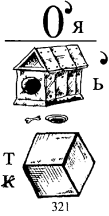
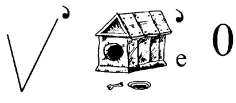
18. Відгадайте ребус

 

 

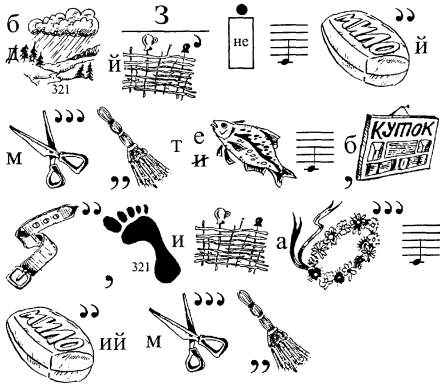
1.4. ДІЛЕННЯ

 

19. Відгадайте ребус

 

 

 

 

 

 

 

 

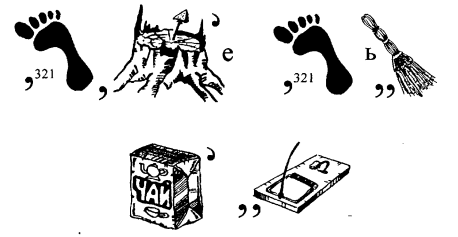
20. Прочитайте ребус

 

21. Відгадайте ребус

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

22. Розгадайте ребус

 

 

 

 

23. Про що говориться в ребусі

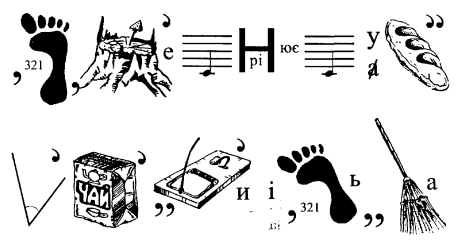
24. Прочитайте ребус

 

 

 

 

 

 

 

 

 

 

 

 

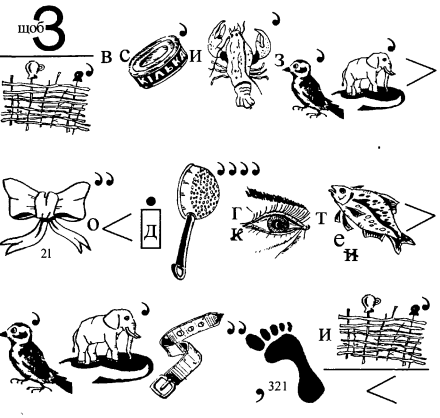
25. Відгадайте ребус

26. Розгадайте ребус

 

 

 

 

 

 

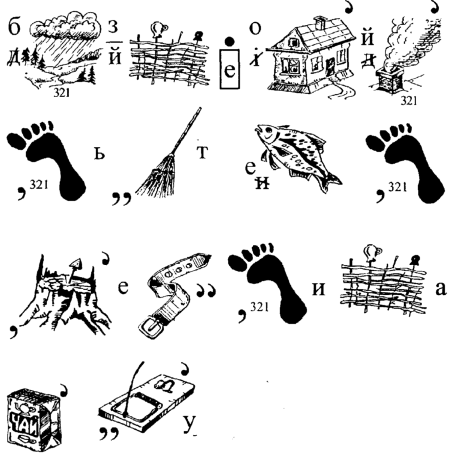
27. Прочитайте ребус

 

 

 

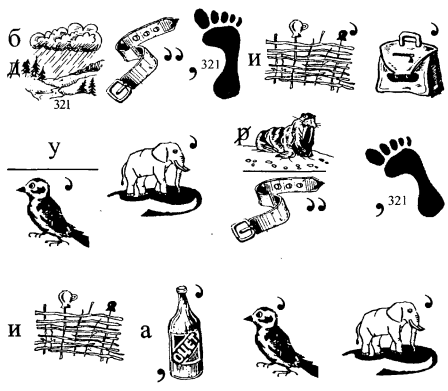
1.5. ДРОБИ

 

28. Про що говорить ребус

 

 

 

 

 

 

 

 

 

 

29. Відгадайте ребус

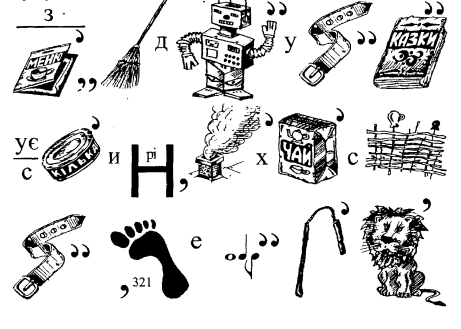
30. Прочитайте ребус

 

31. Що зашифровано в ребусі

 

 

 

 

 

 

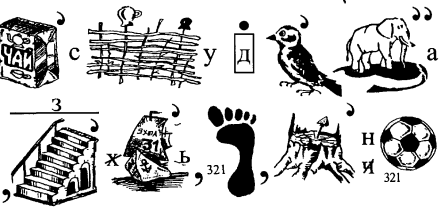
32. Про що йдеться в ребусі

 

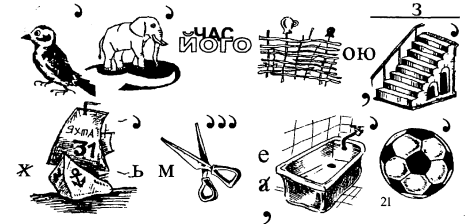
1.6.ОДИНИЦІ ВИМІРЮВАННЯ ДОВЖИНИ

 

33. Прочитайте ребус

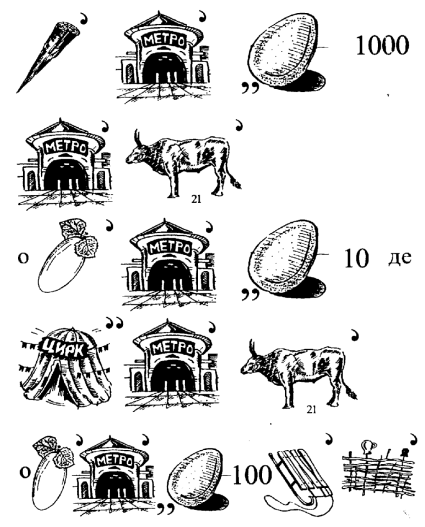
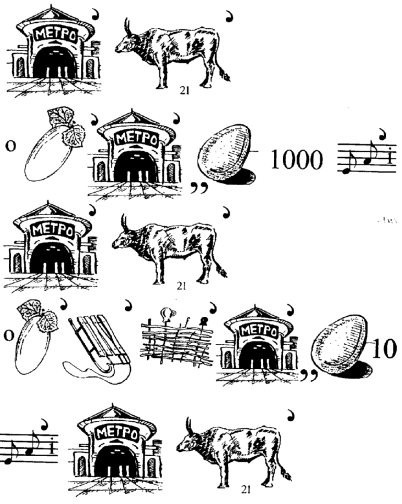
34.  Відгадайте ребус

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

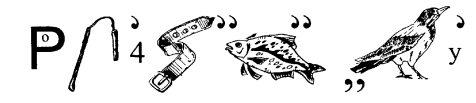
35. Про що йдеться в ребусі

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

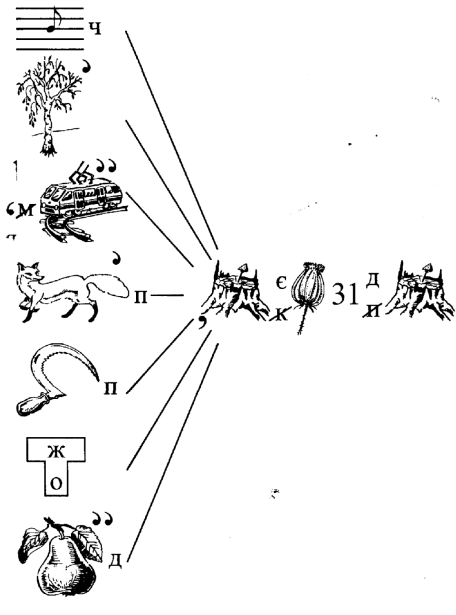
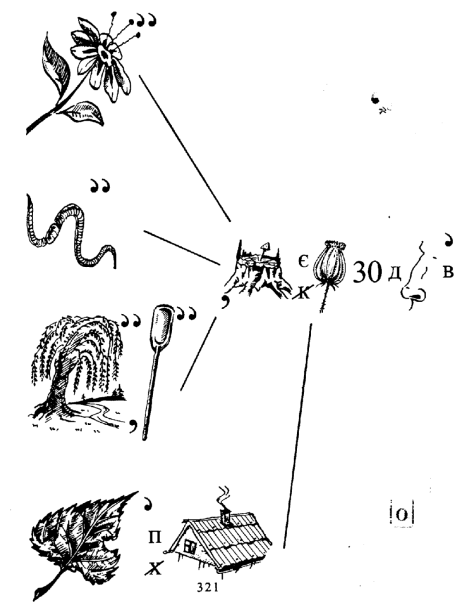
36.  Прочитайте ребус

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

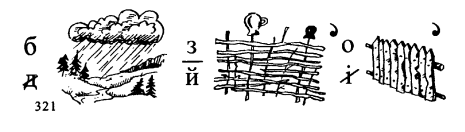
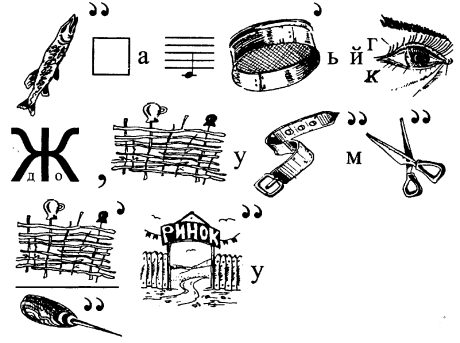
1.7. ГЕОМЕТРИЧНІ ФІГУРИ

 

37. Прочитайте ребус

 

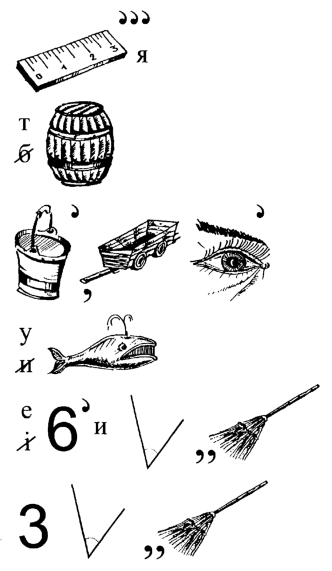
38. Відгадайте ребус

 

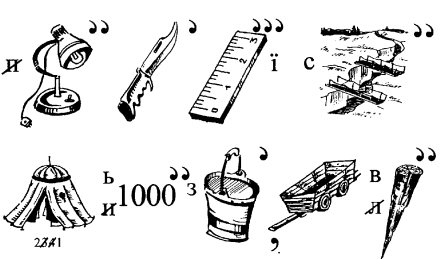
39.Прочитайте ребус

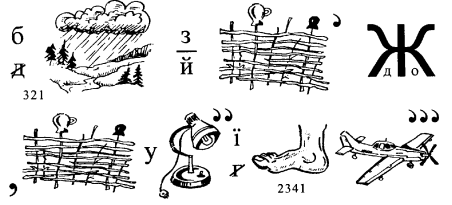
40.Відгадайте ребус

 

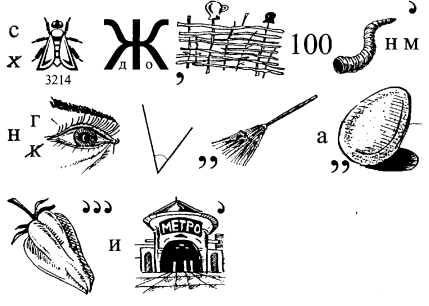
41. Розшифруйте ребус

42.  Прочитайте ребус

 

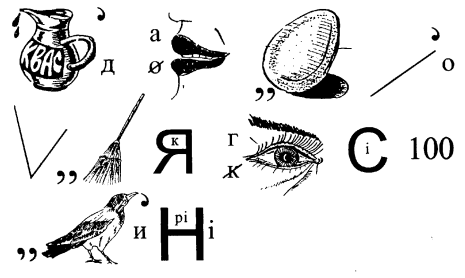
43. Відгадайте ребус

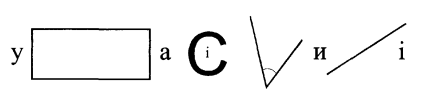
44. Прочитайте ребус

 

45. Розшифруйте ребус

 

 

46. . Відгадайте ребус

 

 

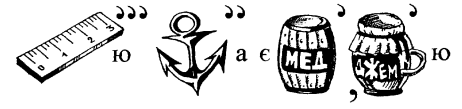
47.Відгадайте ребус

 

 

ВІДПОВІДІ

1.Додавання, доданок, сума, плюс, додати, невідомий доданок. Числа, які додають, називають доданками.

2.Щоб взнати, на скільки одне число більше або менше другого числа, треба від більшого відняти менше.

3.Від переставляння доданків сума не змінюється.

4.Щоб перевірити додавання, треба від суми відняти один з доданків.

5.Щоб знайти невідомий доданок, треба від суми відняти відомий доданок.

6.Якщо у виразі без дужок є тільки додавання, віднімання, то їх виконують в тому порядку, в якому вони записані.

7.Якщо у виразі без дужок є тільки множення і ділення, то їх виконують в тому порядку, в якому вони записані.

8.Задача складається з умови і запитання.

9.Від’ємник, зменшуване, різниця.

10.При відніманні нуля від числа, буде це саме число.

11.Щоб знайти невідоме зменшуване, треба до від’ємника додати різницю.

12.Щоб знайти невідомий від’ємник, треба від зменшуваного відняти різницю.

13.Множення, множник, добуток.

14.Додавання однакових доданків називають множенням.

15.Щоб помножити число на 10, треба до нього справа приписати один нуль.

16.При множенні будь-якого числа на 1 в добутку буде це саме число.

17.При множенні 0 на будь-яке число в добутку буде нуль.

18.Щоб знайти невідомий множник, треба добуток поділити на відомий множник.

19.Ділене, дільник, частка.

20.Число, яке ділять, називають діленим. Число, на яке ділять, називають дільником.

21.Ділити на нуль не можна.

22.При діленні числа на 1 в частці буде це саме число. При діленні 0 на число в частці буде 0.При діленні числа на це саме число буде 1.

23.Ділене дорівнює добутку частки і дільника.

24.Щоб взнати, в скільки разів число більше або менше від другого, треба більше число поділити на менше.

25.Щоб знайти невідоме ділене, треба дільник помножити на частку.

26.Щоб знайти невідомий дільник, треба ділене поділити на частку.

27.Щоб поділити суму на число, можна поділити число на один з множників, а потім на другий множник.

28.Число, записане під рискою, - знаменник дробу.

29.Знаменник дробу показує, на скільки рівних частин поділене ціле.

30.Число, записане над рискою, - чисельник дробу.

31.Частину від числа знаходять діленням.

32.Число за його частиною знаходять множенням.

33.Кілометр-це тисяча метрів. Один метр-це 10 дециметрів. Один метр –це 100 сантиметрів. Один метр – це 1000 міліметрів. Один сантиметр –це 10 міліметрів.

34.В році чотири пори року.

35.Січень, березень, травень, липень, серпень, жовтень, грудень має 31 день. Квітень, червень, вересень, листопад має 30 днів.

36.Щоб знайти площу прямокутника, досить його довжину помножити на ширину.

37.Лінія, точка, відрізок, кут, шестикутник, трикутник, чотирикутник, прямокутник, п’ятикутник.

38.Ламані лінії складаються з відрізків.

39.Щоб знайти довжину ламаної лінії, треба знайти довжину кожного відрізка і додати одержані числа.

40.Сума довжин сторін многокутника-це периметр.

41.Чотирикутник, в якого всі кути прямі, називають прямокутником.

42.Квадрат-це прямокутник, в якого всі сторони рівні.

43.У прямокутника всі кути прямі.

44.У прямокутника протилежні сторони рівні.

45.У квадрата всі сторони рівні.

46.Лінію, яка є межею круга, називають колом.

47.Точка, в якій міститься голка циркуля, - центр кола.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1.9. МАТЕМАТИЧНІ ФОКУСИ «ВГАДАЙ ЧИСЛО»

1.  Запиши чотиризначне число, в записі якого кожна наступна цифра на 1 більша за попередню. Потім запиши інше число тими самими цифрами, тільки в зворотному порядку. Відніми від більшого числа менше. Повтори це ще 3 рази, добираючи інші числа. Порівняй одержані результати. Що ти побачив?

(Результат : 3087 (той самий)

Наприклад. 1234, 4321 (4321 - 1234 = 3087.

2345, 5432; 5432 - 2345 =3087;

3456, 6543; 6543 - 3456 - 3087 і т. д.)

2. Василько задумав число, відняв від нього 4, помножив на 5, додав 3, розділив на 7 і одержав 9. Яке число задумав Василько?

(Василько задумав число 16.)

3. Невідоме число збільшили спочатку на 14, потім ще в 4 рази,
результат відняли від 110 і отримали 18. Яке невідоме число?

(Число 9.)

4. Невідоме число зменшили в 7 разів, до результату додали 25
і одержали 34. Яке невідоме число?

(Число 63.)

5. Задумали число. Зменшили його у 9 разів. До результату додали
37 і одержали 91. Яке число задумали?

(Число 486.)

6. Задумали число. Збільшили його на 9, результат помножили на 6 і отримали 282. Яке число задумали?

(Число 38.)

7. Число 80 поділили на задумане число, до частки додали 13, результат збільшили в 4 рази і отримали 72. Яке задумане число?

(Число 16.)

8. Задумали число. Збільшили його на 52, результат помножили на 7 і отримали 427. Яке число задумали?

(Число 9.)

9. Число 90 поділили на задумане число, до частки додали 29.
Результат збільшили в 5 разів і отримали 170. Яке число
задумали?

(Число 18.)

10.  До числа 3 додали задумане число, суму збільшили в 5 разів
і отриманий добуток відняли від 70. В результаті одержали 15.
Яке число задумали?

(Число 8.)

11.  До 8 додали задумане число, суму збільшили в 9 разів і отриманий добуток відняли від 200. В результаті одержали 65. Яке число задумали?

(Число 7.)

.

 

 

 

 

 

 

 

 

 

1.10. МАТЕМАТИЧНІ КРОСВОРДИ

Математичні кросворди дещо відрізняються від звичай­них. За даними умови треба по горизонталях або верти­калях вписати числа. В кожну клітку вписують одну цифру знайденого числа. Кому і нуль цілих (якщо вони є в числі) не пишуть. Якщо знайдене число наближене, його запи­сують із стількома значущими цифрами, скільки для цього дано кліток.

Якщо умові відповідає не одне число, то вибирають таке значення, яке «пов'язується» з цифрами інших рядків та стовпців кросворда.

Розглянемо приклад. Нехай треба розв'язати кросворд.

По горизонталі. 4. Добу­ток восьми різних простих чисел. 5. Точний квадрат. 7. Процентна сума, яка наросте за 2 роки в ощадній касі на 500 крб. при 2% річних. 8. Число, яке в 6 раз більше від суми його цифр. 9. Просте число. 10. Середня швидкість поїзда, який їхав з А до Б з швидкістю 48 км за годину, а з Б до А — з швид­кістю 72 км за годину.

По вертикалі. 1. Найменше спільне кратне чисел 225, 275 і 335. 2. Добуток трьох послідовних цілих чисел, сума яких 36. 3. Сума чотирьох чисел, про які відомо, що їх суми по три дорівнюють 211307, 206 650, 199 116 і 161 136. 6. Найбільший спільний дільник чисел 1015 і 2465. 7. Точний квадрат. 11. Число, яке в 10 раз більше від суми його цифр.

Кросворд 2

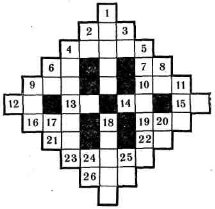
По горизонталі. 2. Точний квадрат. 4. Точний квадрат. 6. Число, яке більше від суми його цифр у 10 раз. 7. Точний квадрат. 9. Точний куб. 10. Точний куб. 12. Ціна товару, яка спочатку дорівнювала 25 крб., але двічі була знижена на 20%. 13. Точний квадрат. 14. Число, кратне 7. 15. Число, кратне 13. 16. Точний квадрат. 19. Точний сте­пінь 2. 21. Число, яке в 5 раз більше від суми його цифр. 22. Добуток двох послідовних парних чисел. 23. Найменше спільне кратне чисел 209, 297 і 363. 26. Число, кратне 11.

По вертикалі. 1. Об'єм прямокутного паралелепі­педа, виміри якого дорівнюють 29, 31, 32. 2. Добуток двох натуральних чисел. 3. Число, кратне 8. 4. Найменше семицифрове число, у якого всі цифри різні. 5. Найбільше семицифрове число, у якого всі цифри різні. 6. Число, кратне   13.   8. Добуток

двох послідовних нату­ральних чисел. 9. Най­більший спільний діль­ник чисел 1134, 2835 і 6237. 11. Найменше спільне кратне чисел 108, 243 і 324. 17. Число, яке більше від суми його цифр у 7 раз. 18. Точний квадрат. 20. Число, кратне 9. 24. Кіль­кість ігор між 7 футболь­ними командами, які зу­стрічаються по одному разу.   25. Просте число.

Кросворд З

По горизонталі. 2. Ціна 1 кг суміші з 6/сг цу­керок по 2,8 крб. і 2 кг цу­керок по 1,68 крб. 4. Най­менше спільне кратне чисел 245, 275 і 385. 6. Число, яке в сумі з числом, записаним тими самими цифрами в зво­ротному порядку, дорівнює 154, причому цифра десятків на 4 більша від цифри оди­ниць. 7. Найменше двоциф­рове просте число.

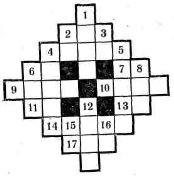
9.

10. Добуток шести послідовних натуральних чисел. 11. Най­більший спільний дільник чисел 8281 і 1001. 13. Середня швидкість руху мотоцикла, який з А до М їхав з швид­кістю 25 км за годину, а назад — з швидкістю в півтора раза більшою. 14. Площа квадрата, периметр якого дорівнює 940. 17. Число хвилин у третині доби.

По вертикалі.   1. Шлях  автомобіля, який першого дня проїхав 30%  шляху, другого дня у цієї   відстані,   а третього і четвертого дня 682 км, що залишилися. 2. Просте число. 3. Число, яке втричі більше за суму його цифр. 4. Добуток п'яти послідовних простих чисел. 5. Кількість робітників на чотирьох заводах, про які відомо, що на І, II і III —34 293 робітники, на І, III і IV — 39 335, на І, II і IV —39436, на II, III і IV —40041 робітник. 6. Сума простих чисел, які не перевищують 100. 8. Вага в тоннах вантажу, для перевезення якого потрібно п'ятитонних грузовиків на 42 менше, ніж грузовиків з вантажопідйомністю 2 т. 12. Добуток трьох послідовних непарних чисел. 15. Число, яке на 9 більше від числа, написаного тими самими цифрами в зворотному порядку. 16. Число, яке в 10 раз більше від суми його цифр.

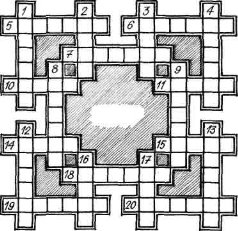
Кросворд. Перша ко­манда (весь клас) колектив­но відгадує слова по гори­зонталі, а друга — по вер­тикалі (мал. 68).

По горизонталі: 5. Компонент дії додавання. 6. Один з місяців року. 7. Одна з величин, що характеризує розмір прямокутника. 10. Сукупність поділок на лінійці. 11. Ста­ровинна російська міра довжини. 14. Знак для позначен­ня числа.  15. Початок дня.  18. Результат дії множення.

19.  Одна з числових характеристик ям, щілин, морів тощо.

20.  Елемент кута.

По вертикалі: 1. Неправильність у розв'язанні. 2. Двоцифрове число. 3. Мі­ра маси. 4. Число, на яке множать. 8. Математична наука, елементи якої вив­чають у початкових класах. 9. Завдання для усного чи письмового         обчислення.

12. Креслярський інстру­мент. 13. Розмір предмета в поперечнику. 16. Десять десятків. 17. Порядкове по­значення предмета.

 

 

Десяткова система

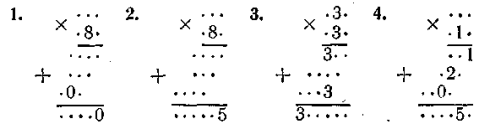
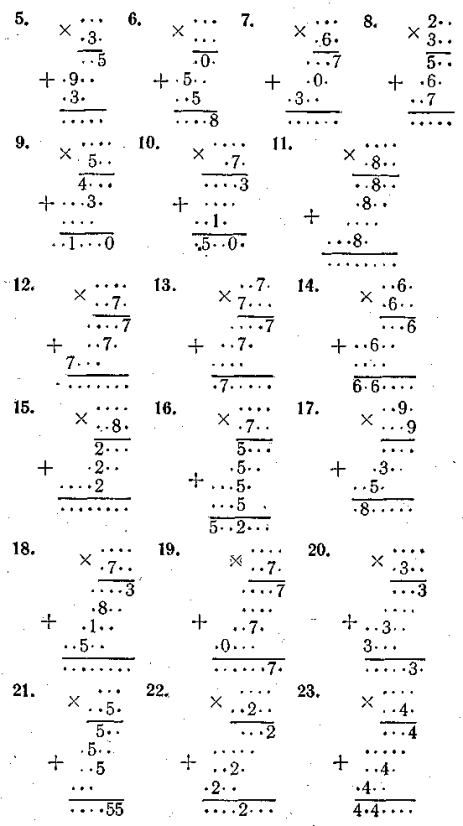
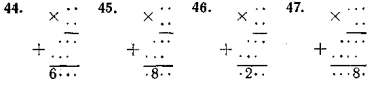
У вправах 36—39 другі стовпчики відрізняються від перших порядком множників, а у вправах 40—43 множники других стовпчиків записані тими самими цифрами, що й множники перших стовпчиків,   але у зворотному порядку.

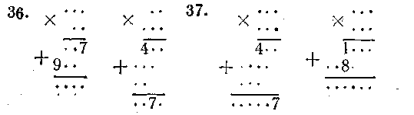
У вправах 44—47 крапками зашифровані  парні цифри.

Відтворення запису множення

Десяткова система

1. В результаті множення на 8 вийшло трицифрове число, а від множення на цифру одиниць множника — чотирицифрове. Отже, цифра одиниць 9, а перша цифра множеного 1. Множене більше від 1000:9 і менше від 1000:8. Оскільки добуток закінчується цифрою 0, то множене 120. Трете множення визначає цифру сотень множ­ника — 5.

3.  В результаті множення на 3 в добутку вийшло чотирицифрове число. Отже, цифра сотень множеного не менша від 3. Цифра оди* ниць множника 1. За останнім добутком цифра сотень множника не менша від 8. Оскільки цей добуток—непарне число, вона дорівнює 9,

4.  З другого добутку видно, що цифра десятків множеного 2, Оскільки добуток закінчується цифрами 51, останні цифри множни-ків: 1 і 1,9 і 9 або 7 і 3. Ці можливості треба перевірити.

5.  За кількістю цифр у добутках видно, що крайні цифри множ­ника менші від 3. Оскільки добуток закінчується цифрою 5, то цифри одиниць множеного і множника відповідно 5 і 1.

6.  Останній добуток закінчується цифрою 5. Оскільки (з пер­шого добутку) цифра одиниць множеного не 5, то 5 — цифра сотень множника. В множеному перша цифра 1,  остання — непарна. Другий

добуток починається з 15. Отже, множене не менше від 1500:9, тобто не менше від 167. Цифра одиниць множника парна і менша від 6. Перевірка показує, що це 4, а множене  177.

7.  Оскільки другий добуток має 3 цифри, то множене менше від 909:6, тобто не перевищує 151. З третього добутку видно, що воно більше від 1300:9, тобто більше від  144.

8.  Цифра одиниць множеного 9 (з третього добутку), а множ­ника 2 (з першого добутку). Цифра десятків множеного не менша 5.

9.  З третього добутку видно, що множене менше від 10 000 : 8= = 1250. Тому цифра одиниць множника 4, а цифра десятків—9. Отже, множник 594. Остання цифра множеного 0 або 5. Беручи до уваги, що множене більше від 1111, маємо два варіанти множеного: 1170 або 1215.

10.  За кількістю цифр у добутках видно, що остання цифра множника 9. Тому остання цифра множеного 7. За другим добутком і додаванням бачимо, що цифра десятків множеного 5. Тому цифра сотень множника 2.

11.  Цифра тисяч множеного 1, крайні цифри множника — по 9. Перший добуток не менший від 10 880. Тому множене не менше від 1209. Але не більше від 1250. Перший добуток не може дорівню­вати 11880, отже, множене 1209.

12.  З першого добутку видно, що цифра одиниць множника не­парна і більша від 7. Отже, це 9. Цифра одиниць множеного 3.

13.  За кількістю цифр у добутках видно, що цифра одиниць множника 9. Тому цифра одиниць множеного 3. Цифра тисяч мно­женого 1, цифра десятків множника 0. З другого добутку видно, що цифра сотень множника 1. Цифра сотень множеного 1, 2, або 3.

14.  Цифра десятків множника 0, а цифри одиниць і тисяч менші від 6. В другому добутку цифра сотень парна, отже, цифра одиниць множеного 7, 8 або 9.

15.  За кількістю цифр у добутках видно, що цифра тисяч множ­ника 9. Цифра тисяч множеного 1, тому цифра одиниць множника 2. З третього добутку видно, що цифра одиниць множеного 8. З того ж добутку видно, що множене менше від 1250, але не менше за 1158.

16.  Перша цифра множеного 1 або 2. Цифра тисяч множника непарна і менша від 5. Тому цифра одиниць множеного 5. Третій добуток визначає цифру десятків множеного — 6. Перевірка пока­зує, що цифра тисяч множеного не 1, а 2.

17.  З першого добутку видно, що множене починається цифрами 10. Тому цифра  десятків   множника 4. Цифра   сотень   множника 0.

18.  Остання цифра множника непарна і більша від 7, тобто це 9. Тому цифра одиниць множеного 7. З третього добутку видно, що множене починається цифрами 10, 11 або 13.

19.  Цифра одиниць множника непарна і більша від 7, отже, це 9. Тому цифра одиниць множеного 3. Додавання в стовпці десятків показує, що в першому добутку цифра десятків 6. Отже, цифра десятків множеного 6. Перша цифра множеного 1, друга —не нуль, але менша від 4.

20.  За кількістю цифр третього добутку видно, що цифра тисяч множеного не менша від 3. З четвертого добутку видно, що вона дорівнює 3. Цифра тисяч множника 1. Цифра сотень множеного 4 або 7. Цифра десятків множника 1 або 2.

21.  З останнього добутку видно, що цифра одиниць множеного 5, а цифра одиниць множника 1 або 3. Але цифра 3 не відповідає другому добутку. Отже, цифра одиниць множника 1. Цифра сотень множеного 5. Тому перші цифри множника—одиниці. Стовпець десятків визначає другу цифру множеного — нуль.

22.  Підрахунок кількості цифр у добутку показує, що множ­ник дорівнює 11201, тому   три   останні   цифри   множеного — двійки.

23.  Перша цифра останнього добутку 3 або 4. Якщо вона 4, то перша цифра множника 1 і перша цифра загального добутку дорів­нюватиме не 4, а 5. Отже, четвертий добуток починається цифрами 34. Цифра сотень множника 2. Цифра десятків множеного 2 або 7 цифра одиниць множника  1 або 2.

24.  Цифри одиниць співмножників З і 3,7 і 7 або 9 І 1.

25.   Третє множення показує, що В² закінчується цифрою J5. Отже, В = 1, 5 або 6. Але В ■ А закінчується на В, а В • Б закін­чується нулем. Отже, В = 5.

26.  Аналогічно до  вправи 25.

27.  З другого добутку видно, що А < 4, але не дорівнює 0 і 1. Отже, А = 2 або 3. З додавання видно, що Е = 9, А — Б + 1, при­чому Б — не 0 і не 1.

28.  З другого добутку видно, що А < 3. З суми видно, що п = = 9, Ж = 0, А = М + 1.' В той же час 5 = 8.

29.  З другого добутку видно, що А > 3. Оскільки А ■ В закін­чується цифрою В, то В = 0, або 5 і А — непарна цифра, або А = 6 і В — парна цифра.

30.  Оскільки С • С і С ■ X закінчуються на С, причому Л ф і 1 С ф 0, то С = 5, а X —непарна цифра. З першого добутку видно, що В = 2 або 7.

31.  З стовпця десятків видно, що □ більший від Д. Оскільки добуток Д • D закінчується Д (причому □ ф 1 і АФ 0), то або д = 5   і  □ — непарна  цифра, або   □ = 6 і Д — парна цифра.

32.  Добутки О на три різні цифри закінчуються на_О¥=0. Отже, О = 5. З кількості цифр видно, що Д<5. Оскільки це непарна цифра, яка не дорівнює 1, то Д = 3. Тоді останні цифри другого добутку 75, а перший добуток 705.

33.  З першого добутку видно, що У = 5 або 6. Але другий добуток показує, що U не 6. Отже, Н = 5, В - непарна цифра. Тому В -парна цифра 1 Ш =0. Як друга цифра множення на 5 ■ = 2 або 7. Оскільки р, першому добутку цифра тисяч менша за 5, то Н =2. Тепер легко побачити, що D = 4, В = 8 І т. д.                              .

34. Оскільки ■ не 0 і не І, а ■ • ■ закінчується цифрою В , то В =5 або 6. Оскільки останні цифри інших добутків різні, то В =6. З додавання десятків видно, що Н = 0, тому И = 5. Оскільки Я - непарна цифра, яка неї і менша за 5, то В =3. Тоді И =8 І D =2, a D =1. З першого добутку знаходимо множене.

35.  Т = 1. Далі випробовуємо значення У. Виявляється, що при У > 3 має бути Р = 0.

37. Друга цифра множника 0, цифра десятків його менша за 4 і непарна. Перевірка показує, що вона дорівнює 1. Отже, множе­не 407, перша цифра множника більша від 1, але менша за З, тобто  2.

38.  Друга цифра множника 0. Друге множення (на 7) визначає цифру сотень —2. Перша цифра другого добутку (друге множення) 1, тому перша цифра третього добутку 6.

39.  З першого добутку видно, що цифра одиниць множника 5, а цифра десятків парна, але менша від 5. Перевірка показує, що ця цифра не 4. Якщо вона 2, то приходимо до множення 743 • 225, яке відповідає умові задачі.

40.  Одна з останніх цифр множника 5. Оскільки добуток 1470 = = 98 • 15 = 42 ■ 35, треба перевірити обидві можливості.

41.  Середня цифра множеного 5. Тому перша цифра його 2 або 7. Якщо вона 7, то останній добуток не матиме середньої цифри 6. Отже, це 2.

Перша цифра множника 3. З другого добутку видно, що цифра одиниць множеного 6. Тоді цифра десятків множника 2.

42.  Добуток одиниць у першому множенні дорівнює 8, 18, 28 або 48. З цих варіантів тільки останній відповідає другому мно­женню. Добуток перших цифр (з другого множення) закінчується нулем. Виходить, перша цифра множеного 5, множника — парна.

43.   Нехай множене А6В, множник CXY. З другого добутку видно, що А або С дорівнює 5. Якщо А = 5, то Х — 7. Але це не підтверджується другим множенням.   Отже,   С = 5, А = 9, 7  або 3.

44.  Оскільки при додаванні переходу нема, то перша цифра дру­гого добутку 6. Отже, перші цифри множників — 8 і 8. Другі цифри — тільки 0 і 6.

45.  Стовпець десятків складається з 2 4-6, або 4 + 4, або 6+2, або 8 + 0. Випробовування показує, що придатний лише останній ва­ріант (60 • 48 = 2880).

46.  У стовпці сотень цифри 2 і 0. Це може бути тільки в разі множення 26 на 88.

47.   Якщо остання цифра 0, то можливий варіант 680 • 66, а якщо не 0, то варіант 668 • 66.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2. МАТЕМАТИЧНІ ЗАДАЧІ ЛОГІЧНОГО ЗМІСТУ

 

1.Три цифри п’ятицифрового числа – одиниці. Знайти це число, знаючи, що воно ділиться без остачі на 72(14112,41112,11160).

2.Три цифри п’ятицифрового числа – четвірки. Знайти це число, знаючи, що воно ділиться без остачі на 315(44415).

3.Знайти число, яке дорівнює квадрату суми його цифр (0,1,81).

4.Знайти двоцифрове і трицифрове числа, сума яких дорівнює 162, знаючи, що сума чисел, записаних тими самими цифрами в зворотному порядку, 504(124,38).

5.Івану і Миколі сказали, що число 150 розкладене на три різні натуральні множники. Івану дали аркуш з записаним середнім за величиною множником, а Миколі – аркуш з записаною різницею двох менших множників. Треба було визначити всі три множники.

Після того як обидва хлопці сказали, що ще не можуть відповісти на запитання, Іван, почувши відповідь Миколи, написав правильну відповідь. Побачивши це, і Микола написав правильну відповідь. Як міркували хлопці?

6.За квадратним столом сиділи чотири студенти. Філолог сидів проти Козира, поруч з істориком. Біолог сидів поруч з Валдейським. Сусіди Шадрова - Єгоркін та хімік. Проти кого сидів історик? (Проти Валдейського).

7. Головоломка моя зародилася в умові дачної квартири. Задача, так би мовити, побутова. Жилиця - назву її для зручності Трійкіною - поклала у спільну плиту 3 поліна своїх дров, жилиця П’ятіркіна -5 полін, жилець Безпаливний, у якого не було своїх дров, дістав від обох громадянок дозвіл зварити обід на спільному вогні. На відшкодування витрат він заплатив сусідкам 8 коп.Як повинні вони поділити між собою плату?

- Пополам, - поспішив заявити хтось. - Безпаливний користувався їхнім вогнем порівну.

- Е, ні, - заперечив другий, - треба взяти до уваги, яку участь у цьому вогні брали дров’яні вкладення громадянок. Хто дав 3 поліна, має одержати 3 коп.; хто дав 5 полін-одержує 5 коп. Ось це буде справедлива дільба.

- Товариші, - взяв слово той, хто затіяв гру і вважався тепер головою зборів.-Остаточні розв’язання головоломок давайте не оголошувати. Нехай кожний подумає над ними(Не можна вважати, що 8 коп. заплачено за 8 полін, по 1 коп. за поліно. Гроші ці заплачено тільки за третю частину від 8 полін, бо вогнем користувалися троє в однаковій мірі. Звідси виходить, що всі 8 полін було оцінено в 8*3, тобто в 24 коп., і ціна одного поліна-3 коп.

Тепер легко зрозуміти, скільки належить кожному. П’ятіркіній за її 5 полін належить 15 коп.; але вона сама користувалася плитою на 8 коп.; отже, їй належить одержати ще 15-8, тобто 7 коп. Трійкіна за 3 свої поліна має одержати 9 коп.; а якщо відняти 8 коп., що належать з неї за користування плитою , то їй належатиме  лише 9-8, тобто1 коп.

Отже, якщо поділити правильно, П’ятіркіна має одержати 7 коп., Трійкіна -1 коп.

 8.Cелянин і чорт

Йде селянин і плаче: «Життя моє гірке! Заїла нужда зовсім! В кишені пару копійок, і ті треба віддати. Хто б мені допоміг?»

Тільки про це подумав, як перед ним з’явився чорт.

- Якщо хочеш, я тобі допоможу. Бачиш цей міст через річку?

- Бачу! - ніяковів селянин.

- Перейдеш через міст-твої гроші-подвояться. І так кожного разу.

- Невже? - говорить селянин.

- Чесне слово! - запевняє чорт. Тільки кожного разу будеш віддавати мені 24коп.

-Я згідний! - відповідає селянин.

Перейшов він один раз-гроші подвоїлися. Кинув чорту 24коп.Перейшов через міст другий раз Гроші знову подвоїлися. Віддав чорту 24коп. і перейшов через міст третій раз. Грошей стало удвічі - рівно 24коп.Згідно договору селянин віддав чорту останні 24коп.

Скільки грошей у селянина було спочатку?(Розв’язування задачі потрібно розпочинати з кінця. Після третього переходу у селянина залишилося 24 коп., які він повинен був віддати.

Отже, після останнього переходу у селянина виявилося рівно 24коп,а значить перед цим у нього було 12коп.Але ці 12коп. залишилися у нього після того, як він віддав 24коп. Значить всього у нього було 36коп. Отже, другий перехід він розпочав з 18коп., а ці 18коп він отримав, як перший раз перейшов міст і віддав 24коп.Отже , після першого переходу у нього було 42 коп. Таким чином, селянин мав в кишені власних грошей -  21коп.)

9.Селяни і картопля

Йшли троє селян. Зайшли на постоялий двір відпочити і пообідати. Заказали зварити картоплі, а самі заснули. Господиня зварила картоплю, але не стала будити постояльців. Поставила їжу на стіл і пішла. Проснувся перший, побачив картоплю, порахував її, з’їв свою частину і знову ліг спати. Незабаром проснувся другий, який не знав, що перший вже поїв. Він порахував решту картоплі, з’їв третю частину і знову заснув. Після цього прокинувся третій, думаючи, що він проснувся першим, він порахував решту картоплі і з’їв третю частину також. Тут прокинулись його друзі і побачили, що залишилося 8 картоплин. Тоді всім все стало зрозуміло. Порахувати, скільки картоплин подала господиня на стіл, скільки картоплин з’їв кожний і по скільки мав з’їсти кожний, щоб всім досталось порівну? (Третій селянин залишив для перших двох 8 картоплин, кожному по 4 штуки. Значить, він сам з’їв 4 картоплини. Легко зрозуміти, другий селянин залишив своїм друзям 12 картоплин, по 6 кожному, значить, сам з’їв 6 картоплин. Звідси слідує, що перший селянин залишив 18 картоплин, по 9 штук на кожного, а сам з’їв 9 штук.

Отже, господиня подала на стіл 27 картоплин, і на долю кожного приходилось по 9 картоплин. Перший селянин з’їв всю свою долю. Таким чином, з 8 картоплин, які залишилися другому дісталося 3, а третьому 5 штук.)

10. Два пастухи

Зійшлося два пастухи, Іван і Петро. Іван каже Петру: «Віддай мені одну вівцю, тоді у мене буде овець у двоє більше, ніж у тебе!». А Петро відповідає: «Ні? Краще ти мені віддай одну вівцю, тоді у нас буде овець порівну!» Скільки овець було у кожного пастуха?(Зрозуміло, що більше овець було у першого пастуха, у Івана. Але на скільки у нього більше, ніж у Петра?

Якщо Іван віддасть одну вівцю не Петру, а комусь іншому, то чи стане в обох пастухів овець порівну? Ні, порівну у них було б тоді, коли б цю вівцю отримав Петро. Значить, якщо Іван віддасть одну вівцю не Петру, а комусь третьому, то у нього все-таки буде більше овець, ніж у Петра, але на скільки? Зрозуміло, що на одну вівцю, тому що, коли прибавити тепер до стада Петра одну вівцю, то в них стане порівну. Звідси слідує, поки Іван не віддасть нікому ні однієї своєї вівці, то у нього в стаді на дві вівці більше, ніж у Петра.

Тепер візьмемося за другого пастуха, за Петра. У нього, як ми знайшли, на дві вівці менше, ніж у Івана. Значить, якщо Петро віддасть одну свою вівцю не Івану, а комусь іншому, то тоді у Івана буде на три вівці більше, ніж у Петра. Але нехай цю вівцю отримає саме Іван, а не хтось інший. Тоді у нього буде на чотири вівці більше, ніж залишилося у Петра.

Але задача говорить, що у Івана в цьому випадку буде рівно вдвоє більше овець, ніж у Петра. Таким чином, у Петра залишиться чотири вівці після того, як він віддасть одну вівцю Івану, в якого стане вісім овець. Отже, спочатку в Івана було 7, а у Петра 5 овець.)

11.Поділ верблюдів.

Батько, маючи трьох синів, розпорядився, щоб після його смерті поділили стадо його верблюдів так, щоб старший син отримав половину стада, середній - третину і молодший – дев’яту частину всіх верблюдів. Батько помер і залишив 17 верблюдів. Сини розпочали поділ, але виявилось, що число 17 не ділиться ні на 2, ні на 3, ні на 9. За допомогою брати звернулися до мудреця. Той приїхав до них на власному верблюді і поділив стадо по заповіту. Як він це зробив? (Мудрець до стада прибавив свого верблюда, їх стало 18. Розділив це число по заповіту: старшому – 9, середньому – 6, молодшому – 2 верблюдів, забравши свого верблюда назад. Секрет полягає в тому, що сума частин на які було поділено стадо не дорівнювала 1. Дійсно, 1/2+1/3+1/9=17/18.)

12. Скільки води в бочці?

 В одній казці господар, наймаючи робітника, запропонував йому наступне випробування:

- Ось тобі бочка, наповни її водою рівно на половину, не використовуючи ні палки, ні  мотузки. Робітник виконав завдання. Як він це зробив? ( Він налив у бочку води так, щоб перехиливши її на бік поверхня води співпадала з верхньою точкою дна і нижньою точкою отвору зверху.)

13. Детективна   історія.

 На столі було виставлено в ряд бокали з недопитим вином. В одному із них була отрута. Потрібно було якнайшвидше знайти в якому бокалі отрута, звівши число проб до мінімуму. На допомогу прийшов професор математики. Він порахував бокали і сказав, щоб вибрали будь-який. Як пропонував професор провести аналіз? (Якщо кількість бокалі виражено не парним числом, то беремо пробу із одного, потім решту ділимо на дві групи, зливаючи з кожного потрошки. Виявляємо в якій групі бокалів отрута і т. д. , поки не дійдемо до бокалу із отрутою.)

14.До числа добавили 0,1 його, а потім відняли 0,1 суми і отримали990.Знайти це число. (1000).

15.До чисел 100 і 10 дописали справа цифру 1.Яке із чисел збільшилося на більше число відсотків?(1001% і 1010%).

16.Вовк просить Зайця підсунутися на 10 грам.

- Так хто  ж міряє відстань грамами? - здивувався Заєць.

- Ти ж учора казав, що до Заячого лісу 2 години ходу! Що відстань міряється годинами? - відповів Вовк.

Як їх помирити?

17.Довести, що середнє арифметичне трьох послідовних непарних, трьох послідовних натуральних і трьох послідовних парних чисел є число натуральне.(Сума трьох послідовних непарних чисел:2п-1+2п+1+2п+3=6п+3, а парних -6п+6.Перший і другий вираз діляться на 3 націло).

18.Відновіть цифру в у числі 1вв2, яке ділиться на 9.Не виконуючи ділення, встановіть, чи ділиться дане число на 12.

19.Як зміниться величина дробу, якщо чисельник збільшити на 200%, а знаменник зменшити на 50%?(Збільшиться в 6 раз).

20.Зібрано 100кг грибів. Аналіз показав 99% їхньої вологості. Після підсушування вологість стала 98%.Яка вага грибів після підсушки?(50кг).

21.Одна сторона прямокутника на 20% більша сторони квадрата, друга – на 20% менша сторони того ж квадрата. Знайти відсоткове відношення площі прямокутника до площі квадрата.(96%).

22.Два потяги рухаються назустріч один одному по паралельних коліях. Один із швидкістю 36км/год, другий-45км/год.Пасажир, який сидить у другому поїзді, замітив, що перший поїзд пройшов мимо його протягом 6 секунд. Яка довжина першого поїзда? (Швидкість переміщення пасажира, який знаходиться в другому поїзді, відносно першого буде 45+36=81км/год=45/2м/с.Довжина першого поїзда буде рівна 45/2*6=135м).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3. ПЛОЩА ЗНАЙОМА І НЕСПОДІВАНА

Вимірюй все, що піддається вимірюван­ню, і зроби таким усе, що не під­дається вимірюванню.

Г. ГАЛІЛЕЙ

Задачі на розрізування фігур і складання з отри­маних частин якихось інших фігур традиційно займають . почесне місце в цікавій математиці. Унікальну ко­лекцію їх зібрано в книзі Г. Ліндгрена «Занимательные задачи на разрезание» (М., 1977). В основі їх лежить відома з часів античної математики за­дача про рівновеликі і рівноскладені фігури. У ви­падку плоских многокутників рівновеликість фігур є необхідною і достатньою умовою їх рівноскладеності. Для многогранників рівновеликість не є достатньою умовою їх рівноскладеності.

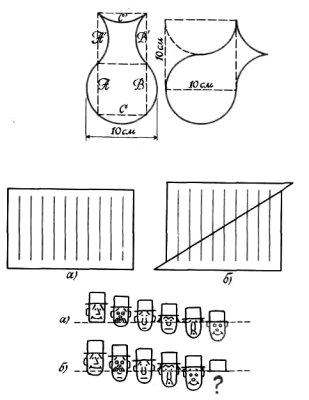
Створено багато цікавих задач на розрізування фігур — від простих, в яких прямокутник перетворюєть­ся в рівноскладений і, зрозуміло, рівновеликий йому квадрат до складніших, коли, криволінійна фігура перетворюється в прямокутник або квадрат (мал. 1).

Численні геометричні софізми засновано на принципі прихованого перерозподілу площ прямолінійних плос­ких фігур. Оскільки за одиницю вимірювання площ беруть площу квадрата, сторона якого дорівнює оди­ниці довжини, то здебільшого на малюнках до про­понованих софізмів площі фігур вже розбиті на оди­ничні квадрати.

1. Тепер накресліть на прямокутному аркуші па­перу 10 однакових вертикальних відрізків, про­ведіть пунктиром діагональ (мал. 2) і розріжте знайдену фігуру по пунктирній лінії. Зсуньте нижню частину прямокутника вздовж розрізу вниз і вліво на відстань між сусідніми лініями і полічіть лінії. Виявляється, їх лишилося тільки 9. Парадокс? Зви­чайно. Ще більшу несподіванку демонструють шість масок. Перемалюйте їх, а потім розріжте вздовж пунк-

Мал. 1-3.

тирної лінії і зсуньте одну частину відносно іншої на відстань між двома сусідніми масками (мал. 3). Тут, справді, є чому здивуватися: від однієї маски залишилася тільки верхівка капелюха. Так виникають перші парадокси, пов'язані з розрізуванням і при­хованим перерозподілом фігур, в результаті чого части­на даної фігури (частина площі, якась деталь фігури, частина малюнка) зникають або з'являються. Що­правда, лінія — це не площа, але маска — це вже не тільки частина площі, а й певні деталі на ній.

Дивно й те, що коли частинки розрізаної фігури повернути на свої місця, то зниклі деталі якимось таємничим чином з'являються. В чому тут річ?

2.  64 = 63.

Перший  варіант  міркувань

А Візьмемо квадрат, площа якого дорівнює 64 (це може бути і звичайна шахова дошка), і розріжемо дану фігуру на три частини (мал. 4, а). Переклавши їх, дістанемо рівноскладений з даним квадратом прямо­кутник (мал. 4, б). Таким чином, із квадрата, площа якого 64, дістали прямокутник, площа якого дорівнює 7X9 = 63 (мал. 4, б).   ■

Другий  варіант  міркувань

А Той самий квадрат розрізали на дві частини (мал. 5, а). Потім першу частину перемістили вгору і вправо. Якщо трикутник NCP відрізати і вмістити на вільному місці в лівому нижньому куті (AQRM), то матимемо прямокутник, площа якого становить 7X9 (мал. 5, б). Отже, 64 = 63.  ■

3.   143=145.

А В результаті перекроювання фігур площа фігури, рівноскладеної з даною, може виявитися не тільки меншою, а й більшою. У прямокутнику з розмірами 11X13 (мал. 6, а) проведемо діагональ, а потім знайдені прямокутні трикутники зсунемо по їхній спільній гіпотенузі в положення (мал. 6, б).

Одержана фігура складається із квадрата і двох рівних прямокутних трикутників. Площа їх дорівнює 12Х 12 + 0,5 + 0,5= 145. Оскільки площа даного прямо­кутника становить 11X13=143, то рівність 143=145 доведено.  ■

4.  63 = 64=65, 168=169, 441=442, 1155=1156, ... А  Квадрат ABCD,  площа  якого S = 64,  розрізали

на чотири частини (мал. 7, а). З них утворили прямо­кутник, трикутник і неопуклий восьмикутник. Квадрат і три одержані фігури рівноскладені. Але площа 5г прямокутника дорівнює площі S₃ трикутника, тобто 65, а площа S₄ восьмикутника дорівнює 63. Таким чином, довели: 63 = 64=65.

У нашому прикладі сторони квадрата було поділено на такі частини, що х = Ь, у = 3. Коли б ми поділили їх на частини х=6 і у=2, то з одержаних двох рівних трапецій і двох рівних прямокутних трикутників не вдалося б утворити прямокутник, лінія B\D\ якого очевидно була б ламаною. Не утвориться прямокутник при х=4—, (/=3— та інших значеннях х і у.

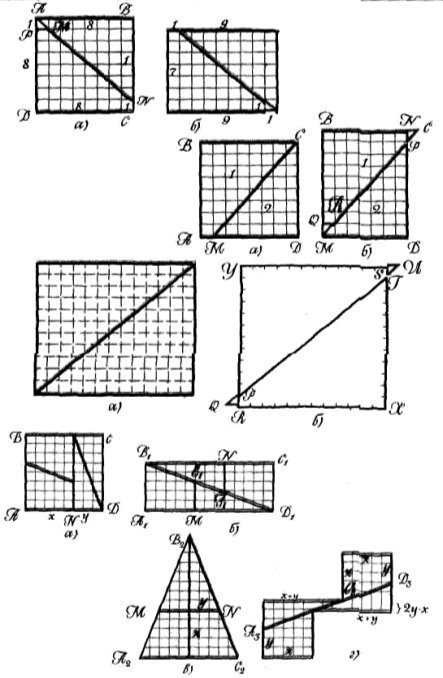
Мал. 4-7.

При х=5 і у=3 дістали прямокутник із сторонами:

х~\-х + у=2х + у=2 ■ 5 + 3=13, ^:=5,5, ==13X5=65.

Якщо сторони  квадрата,  площа якого  169 кв.  од.,

Мал. 8-9.

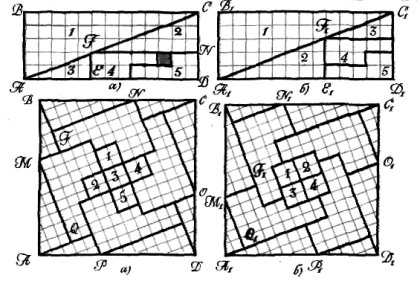
поділити на частини х=8, г/=5, а потім квадрат поділити на чотири частини (пари рівних трапецій і трикутників), то з них утворюється прямокутник із сторонами 2х + і/ = 2 • 8 + 5=21 і х=8. Отже/ Si = 168!

Якщо сторони квадрата 21X21=441 поділити на частини х=13, у = 8, то дістанемо прямокутник, у якого S,=(2x + y)x=(2- 13 + 8)- 13=442. А для квад­рата, площа якого S = 34X34= 1156, при х=2і, г/=13 маємо: S_l=(2x + y)y=(2 • 21 + 13) • 21 = 1155.

Як бачимо, при одних варіантах перетворень квад­ратів S[ — S==l, а при інших 5 —5і = 1. Легко по­казати, що подібні несподіванки чекають на нас при обчисленні площ трикутників, рівноскладених з від­повідними квадратами.   ■

5.  Знову 65 = 64.

▲ Прямокутник ABCD (мал. 8) розрізали по пря­мих лініях на такі 5 частин, що з них потім склали прямокутник заданих розмірів (5X13) од., а зафарбо­ваний квадратик зник. Відбулося «зникнення» одиниці площі) це означає, що 65 = 64.   Ш

6.   141 = 145.

А Квадрат ABCD, площа якого 145, розрізали на 17  містин   (мал. 9 , а).  Потім поміняли деякі з них

Мал.. 10-13.

місцями і знову утворили квадрат A₁ B₁ C ₁D₁ того самого розміру, причому один з п'яти маленьких квадратиків виявився зайвим (мал. 9, б), тобто знову 145=141. 

7.  104 = 105, 168==170, 1=2

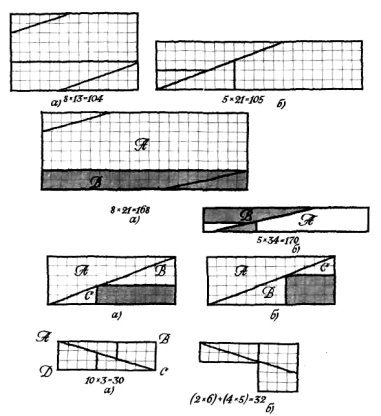
▲ Прямокутник, площа якого 8Х13=104, розріза­ли на чотири частини, з яких утворили прямокутник 5X21 = 105 (мал. 10).  В

А, Прямокутник, площа якого 8X21 = 168, розрі­зали на чотири частини (мал. 11), з яких утворено прямокутник 5X34=170. (Останній прямокутник зоб­ражено у вдвічі більшому масштабі).

▲   Прямокутник розбито на чотири частини (мал. 12). Поміняємо місцями трикутники В і С і обчислимо площу утвореного прямокутника. Він, як і даний прямо­кутник, складається з трьох трикутників (А, В і С) і зафарбованої частини. Але в даному прямокутнику було 16 од. зафарбовано, а в одержаному зафарбовано тільки 15 од. Тому площа його на 1 менша за площу даного і рівноскладеного з ним прямокутника.  

8.  30=32.

▲   Прямокутник ABCD, площа якого 30, розрізали на чотири частини. З них утворили два прямокутники, сума площ яких дорівнює 32 (мал. 13).  ■

9.  1=2=3.

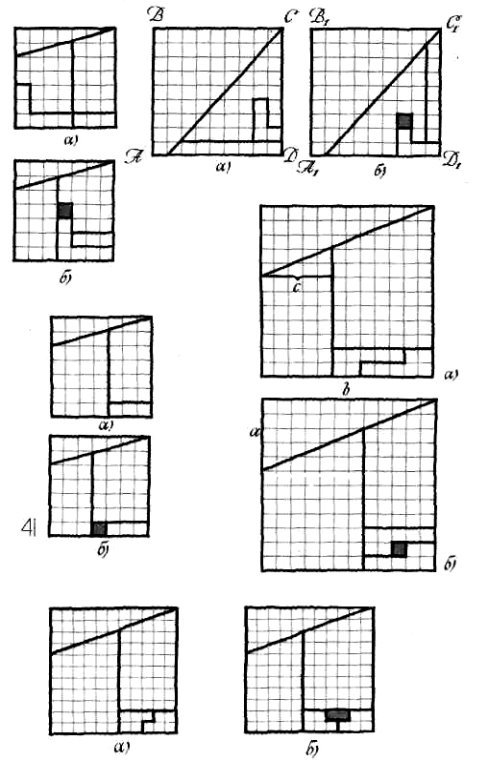
▲   Цікаві парадокси пов'язані з такими розрізуван­нями квадратів, що після перекладання частин знову ті ходять квадрати, з отворами в 1, 2, З і т. д. Найцікавіші  з них подано на мал. 14-19. 

Доведіть формулу, яка виражає залежність розміру отвору, що «виникає» при перекладанні частин роз­різаного квадрата, від довжин а і b катетів найбільшого трикутника і відстані від сторони квадрата до лінії вер­тикального розрізу (мал. 16). Площа отвору в квадрат­них одиницях дорівнює різниці між ас і найближчим до ас числом, кратним Ь. Наприклад, на малюнку 40 ас=25; число, найближче до 25 і кратне Ь, дорівнює 24, тому в результаті перекладання частин розрізаного квадрата дістанемо отвір в 1.

Слід застерегти, що хоча механізми утворення пара­доксів уже відомі читачам, проте точні обчислення, тобто пошук втраченої частини площі, щоразу потребуватиме творчої і чималої роботи. Щоб знайти площу, яку ми втрачаємо, і площу, яка зумовлює видимість цієї анігіляції.

10.  0=2=4 = 6 = 8=...=2я = ...

▲   В утворенні ряду парадоксів з перекроюванням прямокутників, наприклад на малюнку 20, великий три­кутник ABC не відіграє ніякої ролі, і його можна взагалі підкинути, залишаючи тільки розрізаний на чотири частини трикутник ACD. Після перекладання цих частин дістанемо прямокутний трикутник A ₁C₁ D₁ з отвором в 1, ніби рівновеликий даному (мал. 20).

З двох таких прямокутних трикутників можна діста­вати різні варіанти розрізування рівнобедрених трикутників, пов'язані з парадоксами про зникнення кількох   одиниць   площі   (мал.   21).   У   цих   випадках

Мал. 14-18

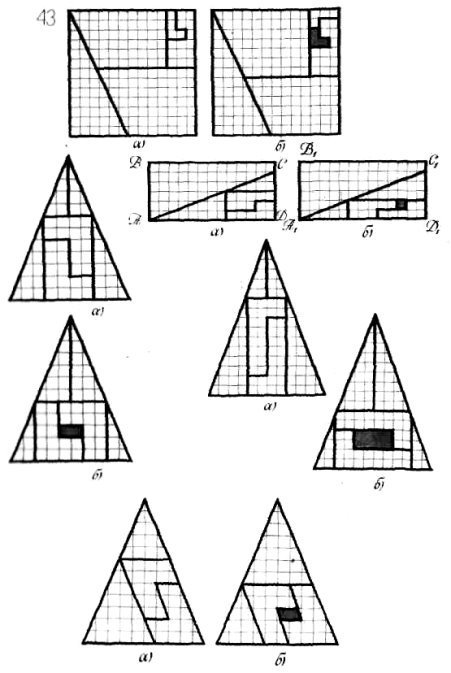
все зрозуміло, але далі доведеться пошукати причини втрати певного парного числа одиниць площі (див. мал. 22 (8), мал. 23, 24 (2), мал. 25 (4), мал. 26 (6)).

Мал. 19-23

11. 0  =1 = 2.

▲  Трикутник, площа якого 60, розрізали на 5 частин (мал. 27), перевернули їх на другий бік і склали з них

Мал. 24-29

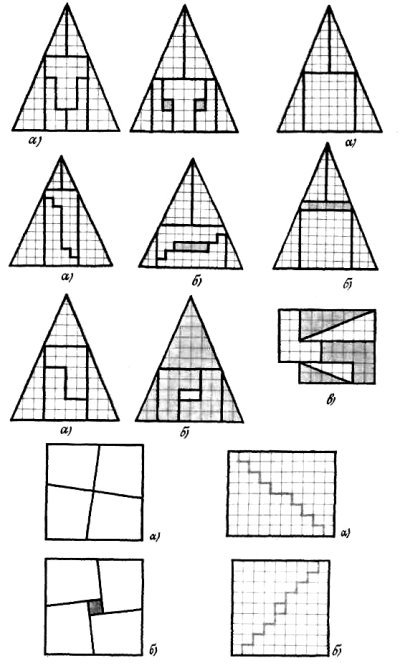
інший трикутник, всередині якого «дірка» з площею 2. 1 Повернувши лицевим боком лише три частини три­кутника, утворимо неопуклий шестикутник, площа якого дорівнює 59. 

12.  Невловима площа.

Перший  варіант  міркувань

▲   Повернемося до квадратів. Цього разу вони демонструють парадокси, засновані на принципово ін­ших методах. Можна, наприклад, розрізати квадрат па чотири рівні частини (мал. 28), а потім скласти їх по-іншому, так, що дістанемо квадрат такого ж розміру, як і даний, але з отвором всередині.

Так само можна розрізати й прямокутник з до­вільним відношенням довжин сторін.

Другий  варіант  міркувань

▲   Прямокутник можна розрізати тільки на дві частини, перекласти їх по-іншому і в результаті дістати прямокутник тих самих розмірів, але з отвором всередині (мал. 29). 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4. МАТЕМАТИКА ШАХОВОЇ ДОШКИ

ЛЕГЕНДА ПРО ШАХИ

Цій легенді понад 2000 років. Індійський цар Шерам покликав до себе винахідника шахової гри, свого підда­ного Сету, щоб нагородити його за дотепну вигадку. Сета, щоб поглузувати з царя, запросив за першу клітку шахо­вої дошки 1 зернятко пшениці, за другу — 2, за третю — 4, за четверту — 8, за п'яту — 16 зерняток і т. д., до шістдесят четвертої клітки.

Цар розгнівався — мовляв, винахідник надто мало про­сить. Однак після підрахунку з'ясувалося, що задовольнити прохання Сети неможливо.

Потрібно було видати: 18 446 744 073 709 551 615 зер­нят.

Це число читається так: 18 квінтильйонів 446 квадриль­йонів 744 трильйони 73 мільярди 709 мільйонів 551 тисяча 615.

Мал..№1

Таку кількість зерняток пшениці можна зібрати лише з урожаю планети, поверхня якої в 2000 раз більша усієї поверхні Землі.

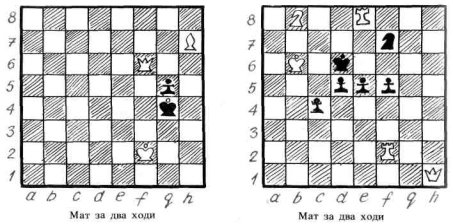
Завдання. Розв'яжи шахові задачі  (мал.  1).

Кінь - єдина шахова фігура, хід якої асиметричний. Найдавніша задача про шахового коня, коли кінь обходить все шахове поле, не заходячи в одну клітинку два рази. Потрібно обійти ходом коня всі клітинки шахової дошки розміром 8х8. Маршрут називається замкнутим, якщо кінь, побувавши на всіх клітинках, повертається у вихідне положення.

   Ніхто не знає, скільки різних способів існує для обходу конем всієї шахової дошки. Чи існує магічний маршрут, слідуючи яким, кінь може обійти всі клітинки шахової дошки, побувавши на кожній лише один раз?

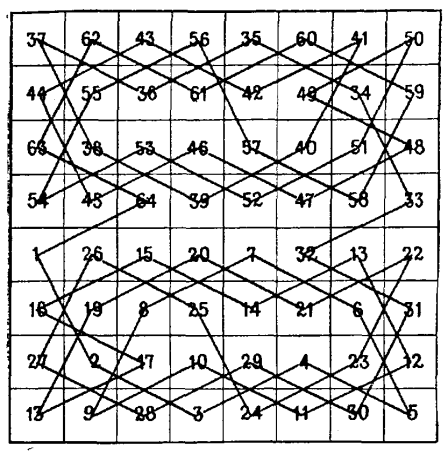
Розв’язок задачі, запропонований Ейлером.

 

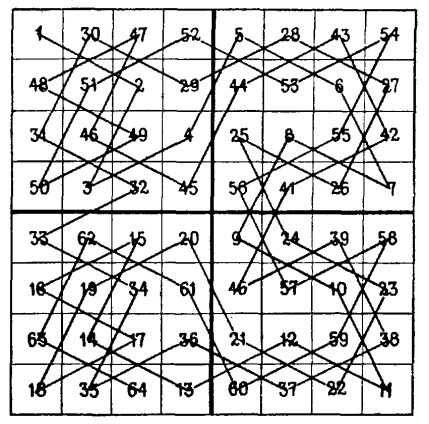
Перший напівмагічний обхід конем всіх клітинок шахової дошки. Сума чисел по будь-якій горизонталі, або вертикалі дорівнює 260.

1.Хід коня

На шаховій дошці розміщено чорні пішаки, як показано на малюнку. Поставте білого коня на будь-яку вільну клітинку шахової дошки з таким розрахунком, щоб цим конем можна було зняти з дошки  всі чорні пішаки, виконуючи при цьому найменше число ходів конем.

 

 

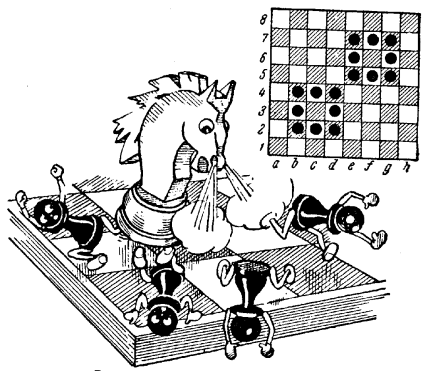
(Всі пішаки можна зняти за 16 ходів. Можна поставити коня так, щоб перший удар нанести по пішаку с2, потім по пішаку b4 і далі d3:b2:c4:d2:b3;e6:g7:f5:e7:g6:e5:f7:g5).

2.Фігуристи на шаховому полі

Фігуристку зацікавили квіти льодового килима. Їй захотілося одним рухом , звичайно з поворотами, проїхати через усі 64 квітки. Рухатися вона вирішила по прямих лініях так, щоб останній шлях привів до тієї квітки з якої починала. Вона пройшла цей шлях по 14 прямолінійних відрізках.

Фігурист, дізнавшись про досягнення дівчинки, поставив перед собою складну геометричну задачу: рухаючись лише по білих клітинках паркету і перетинаючи вершини кліток  не більше, ніж по одному разу, переміститися із лівого верхнього кутка поля в нижній правий куток, побувавши в  кожній білій  клітинці.Він пройшов свій шлях по 17 прямолінійних відрізках.

 

 

 

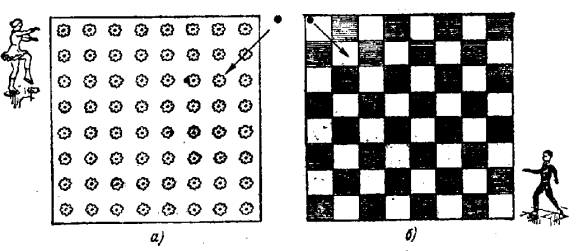
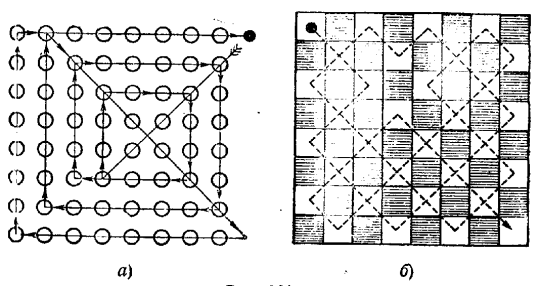
Маршрути фігуристів

 

3.Задача- жарт

Хлопчик намагається перевести шахового коня із лівого нижнього кутка шахової дошки у правий верхній куток так, щоб кінь побував на кожній клітинці дошки по одному разу. Чому він не може цього зробити?

 

 

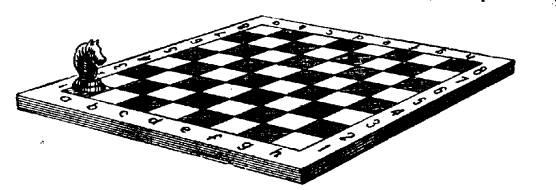
(Хід коня такий, що з чорного поля він може перейти на біле поле і т. д. Шахова дошка має 64 клітинки. Щоб потрапити в правий верхній куток, побувавши на кожній клітинці по одному разу, кінь повинен зробити 63 ходи.

 В початковому положенні  кінь стоїть на чорному полі і прийти має також на чорне поле.

  Це неможливо, так як 63-й хід непарний. А всяким непарним ходом кінь, який займає чорне поле, переводиться на біле поле).

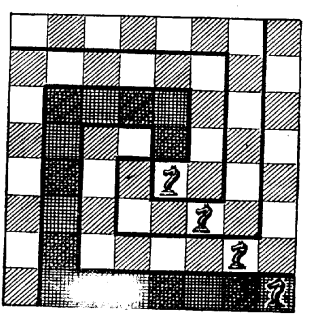
4.Кожному коню по конюшні

На малюнку зображена шахова дошка з 4 конями. Потрібно розрізати дошку на 4 рівні і однакові по формі частини, причому на кожній із частин має залишитися по коню.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5.ЛАБІРИНТИ

    Походження задач про лабіринти сягає у глибоку давнину і губиться в легендах.

     Слово лабіринт в перекладі із грецької означає ходи в підземеллях, катакомби.Найчастіше цим словом  називали штучно створені дуже складні споруди, які складалися з великого числа алей, галерей, перехресть і тупіків які заставляли того, хто туди потрапить, блудити в пошуках виходу.Про такі лабіринти складалися легенди.

Міфічний Дедал побудував на острові Кріт лабіринт для міфічного царя  Міноса. В центрі лабіринту жило чудовище Мінотавр. Ніхто не міг вийти із лабіринту і мимоволі ставав жертвою Мінотавра.Семеро юнаків і семеро дівчат приносили в жертву афіняни чудовиську кожний день. І нарешті, Тезей, вбив Мінотавра і вийшов із лабіринту за допомогою нитки із клубка царівни Аріадни.

   Малюнками лабіринтів прикрашали одяг імператорів. З часом лабіринти стали предметом розваги. Їх перенесли у парки на клумби

 

 

 

 

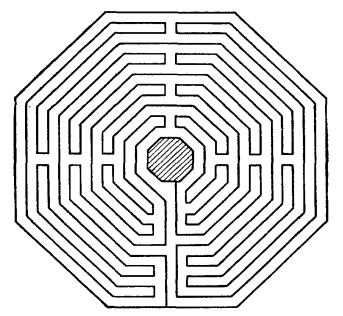
Лабіринт, викладений із каменю на підлозі храму святого Квентіна у Франції.  Вхід знизу по вертикальній лінії.

Лабіринт в Шартрському соборі у Франції.

«Дерновий» лабіринт. Англія. Графство Ессекс 1797р.

 

Італійський лабіринт ХVI ст.

1. Лабіринт.

Йдучи до річки, діти не помітили, як зайшли в парк-лабіринт. Вийти з нього допоміг Юрко. Знайди шлях, яким Юрко вивів загін з лабіринту

 

 

 

 

2.Знайди в лабіринті два шляхи, які ведуть до музею

 

 

 

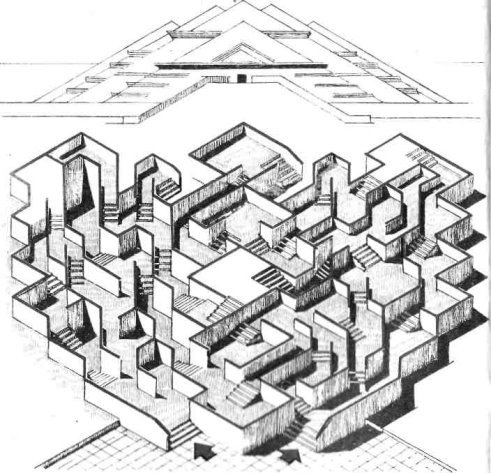
3. Числовий лабіринт. Визнач потрібну дію над двома числами, які розміщені в сусідніх крузі і квадра­ті. Рухатись треба у напрямі стрілки.

 

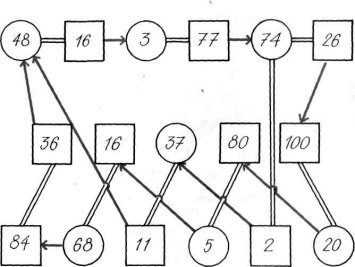
Найдовший шлях по лабіринту такий:

48:16=  3    77 —  3 = 74    74 + 26=100     100 — 20 = 80 80:   5 = 16    16 + 68 = 84    84 — 36 = 48

Знайди коротший шлях.

 

4. Автомобільний лабіринт. Водій має в'їха­ти в автомобільний лабіринт і через 40 секунд виїхати з нього.

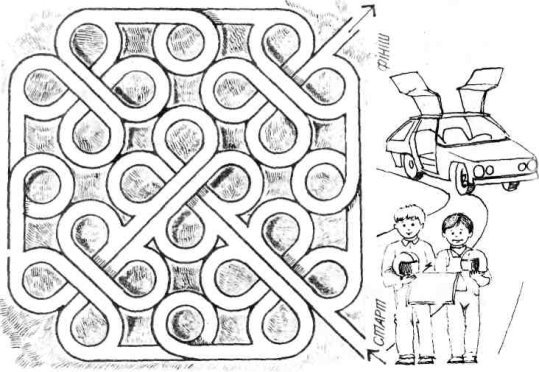
5. Маршрут листоноші. Листоноша розвіз пош­ту в 10 пунктів. Жодного разу він не проїздив по одній до­розі двічі. Який маршрут обрав листоноша? 

 

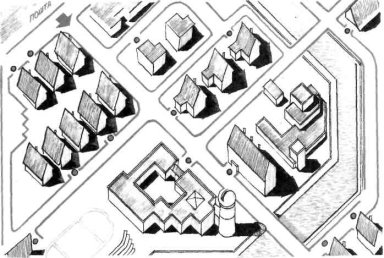
6. Треба пройти з нижнього лівого кута (круг 1) в нижній правий кут (круг 4) таким маршрутом, щоб сума чисел по лінії маршруту дорівнювала 50 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

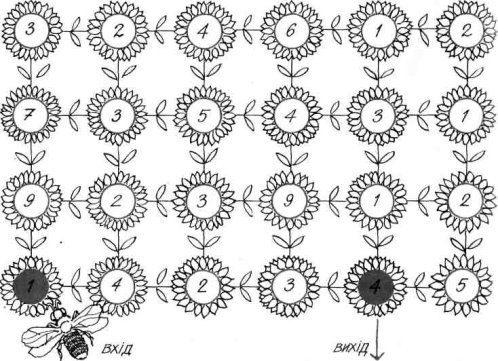
6.ЗАДАЧІ НА ЗВАЖУВАННЯ, ПЕРЕЛИВАННЯ, ПЕРЕКЛАДАННЯ  

1.Серед 80 однакових  на вигляд монет одна фальшива(вона легша). Як за допомогою чотириразового використання шалькових терезів без гир знайти фальшиву монету?

  (Покладемо на обидві шальки терезів по 27 монет. У випадку рівності ваг фальшива монета - в групі з 26 монет. Якщо ж рівності нема,  то фальшива монета в легшій групі з 27 монет. Аналогічно  з групи, де фальшива монета, беруть по 9 монет і кладуть на шальки. І так порівнюють до 1 монети).

 2.Є 27 рівних кубів одного кольору. 26 з них мають однакову вагу. Як за допомогою найменшої можливої кількості зважувань на терезах без гир відокремити куб, вага якого відрізняється від ваги інших, і дізнатися, важчий він чи легший від інших кубів?

   (Аналогічно до попередньої задачі).

  3.Чотири куби однакові на вигляд. Два мають однакову вагу, два інші легші і теж  мають однакову вагу. Скільки потрібно зважувань на шалькових терезах без гир, щоб відокремити важчі куби?

   (Покладемо на різні шальки терезів два куби. Якщо вони однакової ваги, то порівняємо перший і третій куб. Якщо перший важчий, то порівняємо перший з четвертим).

  4.Три купці повинні поділити між собою 21 бочку квасу, із яких 7 повних, 7 повних наполовину і 7 порожніх. Як вони можуть поділити між собою все це, щоб кожний отримав однакову кількість квасу, однакову кількість бочок. Переливати квас із бочки в бочку не можна.

   (Першому дісталося - 2 повних, 3 повних наполовину, 2 порожні.

    Другому - 2 повних, 3 повних наполовину, 2 порожні.

   Третьому - 3 повних , 1 повна наполовину, 3 порожніх).

  5. Старовинна головоломка. Маємо 8 мо­нет однакової вартості, серед них одна фальшива. Фальши­ва монета трохи легша за інші. Як визначити фальшиву монету двома зважуваннями на терезах з двома шальками без гирок? 

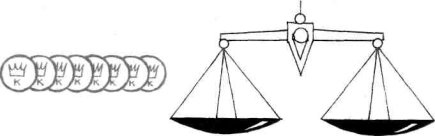
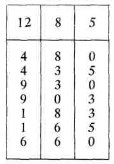
6. Про бочки і хлібний квас. Як поділити на 2 рівні частини 12 відер хлібного квасу, налитого у дванадцятивідерну бочку, користуючись для цього порожніми бочками: восьмивідерною і п'ятивідерною?

Відгадай цю головоломку, користуючись записами таб­лиці.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

7.ЛОГІЧНІ ЗАДАЧІ

Для шукача істини немає нічого кращо­го за саму істину, і не потрібно нехтувати істиною і зверхньо дивитися на тих. хто висловив її або передав: істиною нікого не можна принизити — навпаки, істина облагороджує кожного.                                                                                                 АЛЬ-КІНДІ

1. Взяли шість аркушів паперу. Деяк: з них розі­рвали   на   сім   частин.   Потім   деякі   з   частин   знову розірвали на сім частин.  Після цього усіх  клаптиків виявилося  67.  Доведіть,   що  під  час  підрахунку  до­пущено помилку.

2. У Змія Горинича 1000 голів. Богатир може відтяти за один раз 33, 21, 17 або 1 голову, але негайно відро­стають відповідно 40, 0, 14 або 10 голів. Якщо ж відтя­ти всі голови, то нові голови вже не виростуть. Чи може
богатир перемогти Змія Горинича?

3. У бідного лицаря було дві дуже правдиві дочки Ельза і Жанна. Навіть 1 квітня вони говорили правду. Тільки в день народження сестри могли сказати не­правду, і то лише тоді, коли у них запитували про день народження. 6 квітня 1442 року якийсь подорожній за­питав про день їхнього народження. Ельза відповіла: «Він був учора», Жанна сказала: «Він буде завтра». Наступного дня подорожній повторив своє запитання.
Ельза знову відповіла: «Він був учора», Жанна мовила: «Він буде завтра». Коли ж у Ельзи і Жанни був день народження?

4. Задача-диверсія. Під час другої світової  війни група англійських математиків запропонувала скинути на територію фашистської Німеччини листівки з текстом такої задачі: «На столі лежать 10 гаманців. У кожному з них 10 однакових монет. У дев'яти гаманцях монети справжні  (масою по 10 г кожна), а в одному гаманці всі монети фальшиві   (масою по  11 г кожна). Як за допомогою терезів і набору важків визначити лише од­ним зважуванням гаманець із фальшивими монетами?»

На розв'язування цієї задачі співробітники одного англійського науково-дослідного центру витратили по­над 10000 годин, чим, за підрахунками керівника цен­тру, завдали значних збитків воєнному потенціалу Англії. Тому, очевидно, скоріше жартома, ніж всерйоз, англійські математики й запропонували нанести таких же збитків задачею-диверсією своєму противникові. Задача складна і водночас елементарна. Сподіваємося, що ви розв'яжете її швидше, ніж англійські математики.

5. Жертва «товстої Верти». В першу світову війну німці обстрілювали Париж з велетенської гармати, яку французи прозвали «товстою Бертою». Ефект бомбар­дувань був невеликий.   Інколи доходило до курйозів. Якось в останній день одного з місяців війни снаряди
впали на старовинне кладовище. Все обійшлось. Сна­ряди зруйнували лише гробницю якогось воїна часів Відродження, прикрашену статуєю воїна з мечем, вико­нану в натуральну величину. Одна з вечірніх паризь­ких газет відгукнулась на цю подію логічною задачею, яка викликала справжню сенсацію. Ось її умова. Якщо помножити число місяця, коли це трапилося, на довжину (в ліктях) списа, який був в руці статуї, потім резуль­тат помножити на половину віку похованого воїна, а новий результат — на половину років від смерті воїна до часу, коли в його гробницю влетів снаряд товстої Берти, то буде 451 066.

Скільки років прожив воїн і в якому році його похо­вано?

6. Задача Льюїса Керролла. Як тільки король ді­знався,  що його  казна  майже  порожня  і  гроші,  які лишилися, доведеться витрачати економно, він відразу ж вирішив прогнати як можна більше своїх радників-
мудреців. їх у короля було дуже багато. Всі мудреці мали вельми імпозантну зовнішність, благородні сивини і носили розкішні мантії із зеленого оксамиту з золоти­ми ґудзиками. Єдине, що можна було б поставити їм у провину,— це суперечливість порад, які вони давали королю з будь-яких питань, і надмірну пристрасть до їди і питва з королівського столу (апетит у всіх мудре­ців був чудовий!).

Але за давнім законом, порушити якого не міг ні один король, при дворі завжди мало бути стільки мудреців, щоб серед них неодмінно знайшлися: сім слі­пих на двоє очей, два сліпих на одне око, п'ять зрячих на обоє очей, дев'ять зрячих на одне око.

Скільки мудреців довелося королю залишити при дворі, щоб не порушити давнього закону?

7. Задача Льюїса Керролла. Одному чоловікові дуже хотілося потрапити до театру. Квиток коштував 1 ши­лінг 6 пенсів, а  грошей в цього чоловіка було лише 1 шилінг (1  шилінг становить 12 пенсів). Подумавши, чоловік   вирішив   закласти   свій   шилінг   у   лихваря.

Лихвар уважно оглянув монету і, переконавшись, що вона не фальшива, дав чоловікові під заклад 8 пенсів. З 9 пенсами і квитанцією на 1 шилінг у кишені чоловік вийшов від лихваря і зустрів на вулиці приятеля, якому запропонував купити квитанцію за 9 пенсів. Тепер у чо­ловіка було 9 пенсів від лихваря і 9 пенсів від продажу квитанції. Цієї суми саме вистачило, щоб купити кви­ток у театр. Питається, хто і скільки втратив внаслідок усіх операцій?

8. Добрий чоловік порадив Іллі Муромцю: «Виру­шиш в дорогу — дістанешся до розвилки доріг. По­їдеш однією з доріг — коня загубиш, другою — сам за­гинеш». Вирішив Ілля пожертвувати конем, але, ді­ставшись до роздоріжжя, задумався: яка із доріг чим загрожує? Аж бачить на стовпчику написано: «Якщо хочеш дізнатися, якою дорогою тобі їхати, постав зу­стрічному мандрівникові одне запитання, на яке ти почуєш відповідь «так» або «ні». Але знай, що мандрів­ник може бути чоловіком, який завжди говорить тіль­ки правду або тільки неправду. Зумієш поставити пра­вильне запитання, із відповіді мандрівника довідаєшся, що на якій дорозі тебе чекає». Озирнувся Ілля, а біля роздоріжжя стоїть дідусь-мандрівник. Яке запитання Ілля йому поставив?

9. Кожум'яку мали покарати за те, що, розсердив­шись, він подер багато шкір, які виробляв для багатія. Суддя був аматором логіки і вважав, що у всьому ви­нуваті  ті,  хто  розсердив   Кожум'яку.   Щоб   виручити
доброго   молодця,   запропонував   йому   таку   задачу: «Перед тобою двоє дверей, одні ведуть на волю, дру­гі — в  неволю.   Біля  кожних  стоїть охоронець.  Вони абсолютно схожі, але один говорить тільки правду, а другий — тільки неправду. Постав лише одне запитання будь-якому охоронцеві і за його відповіддю знайди две­рі, які ведуть на волю. Знайдеш — будеш вільний, не знайдеш — бути біді». Кожум'яка знайшов, які двері вели на волю, і був звільнений. Яке запитання він поста­
вив охоронцеві?

10. Логік потрапив на острів, на якому жили два племені - правдолюби і брехуни. Перші говорили тіль­ки правду, а другі — тільки неправду.

Опинившись на роздоріжжі, логік запитав у зустріч­ного остров'янина, яка з двох доріг веде в село. Логі­ку не було відомо, з представником якого племені він розмовляє. Все ж він поставив лише одне запитання,

з відповіді на яке точно довідався, якою дорогою по­трібно йти, щоб потрапити в село. Яке запитання він поставив?

11Логік опинився на острові, заселеному трьома племенами.   Люди   одного   племені   говорили   завжди правду, другого — тільки неправду, а третього — чергу­вали у відповідях правду з неправдою. Зустрівши остро­в'янина, логік поставив перед ним два запитання, які вимагали точних відповідей («так» або «ні»), і тут же дізнався, з представником якого племені він розмовляв. Які питання поставив логік?

12. На острові Трисільському було всього три села: Правдиве, Напівправдиве і Неправдиве. Зрозуміло, що жителі першого села завжди говорили правду, друго­го — чергували   у   відповідях    правду   з    неправдою (перша відповідь мешканця цього села могла бути як
правдою, так і неправдою), жителі Неправдивого завжди говорили неправду.

Логік зустрів відразу п'ятьох остров'ян: Косого, Бо­роду, Кирпаня, Аваса і Довговуха. Бажаючи довіда­тися, хто з них з якого села, логік попросив перших двох розповісти йому по порядку, хто з якого села ро­дом. Косий відповів, що Борода — напівправдивець, Кирпань - правдивець, Авас — напівправдивець, а Довговух — неправдивець; Борода відповів, що Ко­сий — напівправдивець, Кирпань — неправдивець, Авас — правдивець, Довговух — напівправдивець. З цих від­повідей логік встановив, хто з п'яти остров'ян з якого села. Як він міркував?

13.      Стомившись від суперечок і літньої спеки, три давньогрецьких мудреці  прилягли спочити  і заснули. Поки вони спали, хтось із перехожих вимазав сажею їхні лоби. Прокинувшись і подивившись один на одного, мудреці розвеселились і почали сміятися, бо кожному
    здавалось, що двоє інших сміються один над одним. Нараз один з мудреців перестав сміятися: він здога­дався, що його власний лоб також вимазаний. Як він міркував?    

Відповіді.

1.         Кожного разу, коли один аркуш паперу рвали на сім частин, кількість клаптиків збільшувалася на 6. Оскільки спочатку було 6 аркушів паперу, той остаточне число їх мало бути кратним шести.
2.         Богатир міг відтяти голову Змієві в такій послідовності: 1000-21*47 тоді 13-1 тоді12+10 тоді 22-21 тоді 1-1=0.
3.         6 квітня — день народження Ельзи, її відповідь у цей день була  неправильною. З тих же міркувань встановлено, що день народження Жанни — 7 квітня.
4.         З першого гаманця потрібно взяти одну монету, з другого — дві, з третього — три,  ...  , з десятого - десять, усього 55 монет.  Якщо їх  маса  становитиме (550 + п), де п більше-рівне 1 і менше рівне 10, то фальшиві монети в гаманці з номером п.
5.         Якщо розкласти число 451 066 на прості множники, то дістанемо 2*7*11*29*101. Пам'ятаючи, що все трапилося в останній день місяця, приходимо до висновку,  що бомбардування відбулося 29 числа:
   інші множники або комбінації їхніх добутків не задовольняють умови задачі. Оскільки 29 — останній день місяця, то це було в лютому високосного року. Протягом першої світової війни був тільки один високосний рік— 1916.

                    Довжина списа, очевидно, становила 7 ліктів: спис завдовжки 2 лікті був би занадто коротким, а 11 лік­тів — занадто довгим. Лишаються три співмножники: 2, 11 і 101. Число 101 не може бути половиною років, які прожив солдат: 202 роки — нереальна тривалість життя. Отже, йому могло бути або 22 роки, або 44. Тоді 101 — це половина років, які минули від дня його смерті до 1916 року. Це означає, що він помер у 1714 ро­ці (1916 — 2- 101). Але це суперечить тій частині умови задачі, де говориться, що статуя була в стилі Відро­дження. Адже французьке Відродження закінчилося значно раніше 1714 р. Тому остаточний висновок має бути таким. Воїн прожив 22 роки. Половина років, які минули від дня його смерті, це: 2X101=202 роки. Минуло, таким чином, 404 роки. Тому помер він у 1916 — 404=1512 році.

6.         Розв'язання Льюїса Керролла:

Хоть суров закон, но он

Королем был обойден:

Кто хитер, сумеет ловко

Обойти закон уловкой.

Семь слепых и зрячих пять

Дважды стал король считать.

Мысли ход своей чудак

Обьяснить изволил так:

«Тот, кто слеп на оба глаза,

 Явно слеп на глаз один.

Тот, кто видит в оба сразу,

Может видеть й одним».

Дальше ясно все без слов:

Лишь шестнадцать мудрецов

Остается при дворе

Наносить урон казне.

7.                    Відповідь-Льюїса Керролла:

Ви, зрозуміло, думаєте, що в збитку виявився прия­тель заповзятого театрала і що втратив він 6 пенсів? Мій юний друже! Ваша відповідь неправильна, але ро­бить вам честь, бо показує, що ви не маєте ні найменшого уявлення про те, як діють лихварі: адже в своєму розв'язанні ви виходили із того, ніби лихварі займаю­ться своїм ремеслом безкорисливо.              9. Можливі чотири варіанти комбінацій дверей і охо­ронців:

1. Двері на волю. Охоронець — правдолюб.

2. Двері   на   волю.   Охоронець  говорить   неправду.

3. Двері в неволю. Охоронець — правдолюб.
4. Двері  в  неволю.  Охоронець говорить  неправду.

 Кожум'яка запитав одного з охоронців: «Що скаже твій товариш про    двері, які ти охороняєш?» У пер­шому і другому випадку він би почув відповідь: «Він скаже, що вони ведуть в неволю». У третьому і четвер­тому випадку відповідь буде: «Він скаже, що вони ве­дуть на волю».

10.                Одне з  можливих запитань може бути таким: «Якщо запитати будь-якого твого одноплемінника, чи веде ця дорога в село, чи відповість він «так»?» Якщо при цьому логік покаже на дорогу, яка веде в село, то
    кожний острів'янин відповість «так», якщо на дорогу, яка не веде в село, то кожний відповість «ні».
11.                Логік двічі запитав острів'янина:  «Чи  чергуєш ти правду з неправдою?» Почувши у відповідь двічі «ні», логік дізнався б,  що перед ним представник племені правдолюбів, дві стверджувальні відповіді говорили б про те, що перед ним представник закоренілих брехунів,
    відповісти «так» і «ні» міг лише представник третього племені.
12.                Косий, Борода і Авас — неправдивці, Кирпань -напівправдивець, Довговух — правдивець.
13.                Кожний з мудреців міг думати, що його лоб чис­тий. Перший переконаний, що його лоб чистий, і сміє­ться  над забрудненим  обличчям  другого  і  третього.

Задачі.

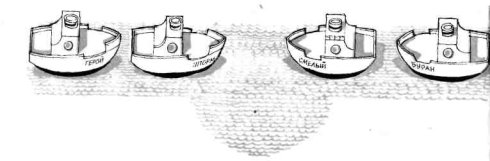
14. Зустріч теплоходів. По річці пливуть тепло­ходи «Герой» і «Шторм», а назустріч їм «Смельїй» і «Бу­ран». Річка тут така вузька, що двом кораблям розминутися важко. Але у цьому місці є затока, в якій може поміститися один теплохід. Як теплоходам розійтися?

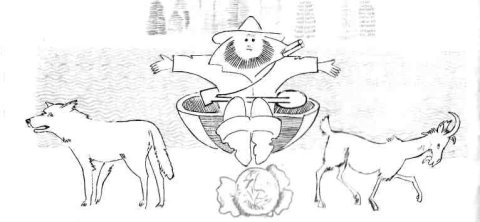
15. Вовк, коза і капуста. (Старовинна задача.) Мисливцю треба перевезти через річку вовка, козу і капусту. Човен настільки малий, що в ньому можуть по­міститися мисливець і з ним або вовк, або коза, або капуста. Вовка не можна залишати з козою, а козу з капустою. Що робити мисливцю? 

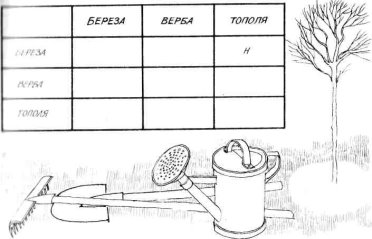
16. Садіння дерев. На згадку про прогулянку дівчатка  — Береза, Верба і Тополя — посадили три дерева: березу, вербу і тополю. Жодна з них не посадила дерева, ці і якого пішло її прізвище. Яке дерево посадила кожна дівчинка, якщо відомо, що Береза посадила не тополю?

Розв'яжи задачу, користуючись таблицею.

 

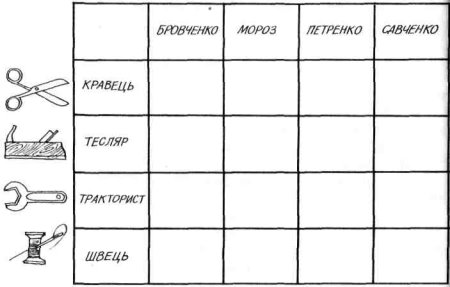
17. Бровченко, Мороз, Петренко і Савченко живуть на одній вулиці. Один з них кравець, другий — тесляр, тре-j тій — тракторист, четвертий — швець.

Одного разу кравець прийшов до свого друга тесляра, щоб попросити його полагодити двері, але йому сказали, що тесляр допомагає Морозу ремонтувати дах. Визнач професію кожного, якщо відомо, що: 1) Петренко не тес­ляр, а Савченко майже не знайомий з теслярем. 2) Мороз не вміє водити трактор, Петренко з трактористом добре знайомий. 3) Петренко не кравець.

Розв'яжи задачу, користуючись таблицею:

 

 

 

 

 

 

 

 

 

 

 

 

8.         МАТЕМАТИЧНІ ІГРИ

1. Гра «Танграм». Це ста­ровинна гра, якою захоплю­валися не тільки школярі, а й вчені. Щоб провести гру як змагання, треба з цупкого паперу вирізати два квадра­ти із стороною ЗО см. Кожен квадрат ділять на 7 частин за поданим зразком.

Грають дві команди, по 7 чоловік у кожній.  Перша

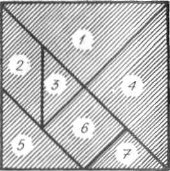
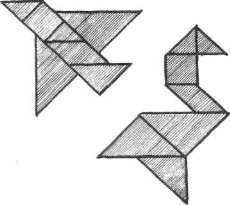
команда повинна з частин квадрата скласти за зразком фігуру гусака, а друга — літака.

Зауважимо, що з елемен­тів танграма можна скласти багато різних фігур: курку, кота, молоток, літак, кора­бель, поїзд тощо.

2. Морський бій

Гравців двоє. На аркушах у клітку кожен креслить по два квадрати із стороною у 10 кліток. Лівий квадрат вико­ристовується для позначення пострілів по ескадрі супер­ника, а на правому гравець розміщує свою ескадру з п'яти кораблів. Чотири кораблі бойові: на дві, три, чотири і п'ять щогл (кліток). П'ятий, чотирищогловий, корабель — госпі­таль (на малюнку штрихується).

На малюнках видно, як розмістили кораблі Тарас і Юрко. Зрозуміло, що в ході гри командири ескадр (гравці) не показують один одному розміщення кораблів.

По вертикалі клітки квадратів позначені числами, а по горизонталі буквами. За допомогою числа і букви визна­чається місце будь-якої клітки квадрата. Наприклад: 9, б; 9, в; 9, г — клітки трищоглового корабля Тараса, а 3, з; 4, з; 5, з — клітки такого самого корабля у Юрка. Під час гри клітки називають так: «дев'ять-бе, дев'ять-ве, де-в'ять-ге».

Правила гри. Гравці по черзі роблять по З постріли. Щоб зробити постріл, гравець називає клітку, яку хоче ви-

бити, наприклад, «чотири-ге». Цю клітку він позначає хре­стиком або точкою на своєму лівому квадраті, а його супер­ник — на квадраті своєї ескадри.

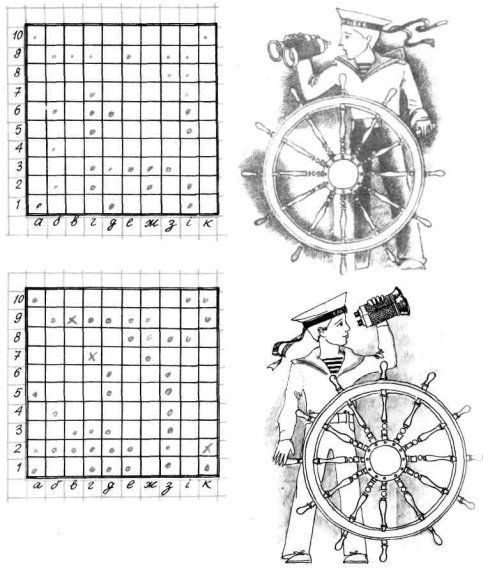
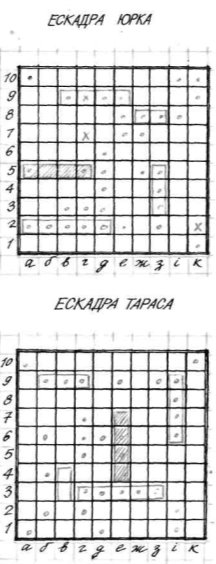
Кожного разу, коли гра­вець зробить 3 постріли (залп), його суперник по­відомляє результати. На­приклад, перший залп Та­раса був такий: 7, г; 9, г; 2, к. На малюнках ці постріли позначені хрестиками. Про результати залпу Юрко по­відомив так: «Один раз попав у чотирищогловий корабель». Яким саме по­стрілом влучено у кора­бель — не повідомляється.

Гра триває доти, доки в когось із гравців не будуть потоплені всі бойові кораблі. Корабель вважається по­топленим у тому разі, коли суперник влучить в усі кліт­ки, з яких він складається.

Корабель-госпіталь то­пити забороняється. Якщо в ході бою гравець влучить у госпіталь, то гравця штра­фують. Супернику надаєть­ся право зробити не З, а 6 пострілів.

Результати бою між ес­кадрами Тараса і Юрка видно з малюнків. Переміг Тарас — у нього залишився неушкодженим двощогло­вий корабель.

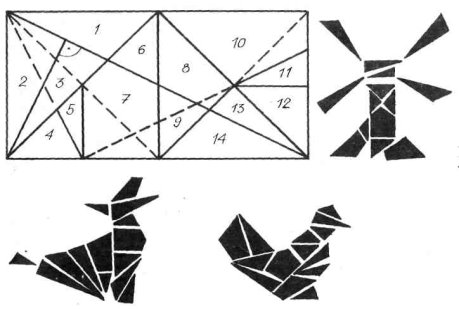
3. Стомахій — старовинна гра, яку винайшов Архімед. Прямокутну смужку, довжина якої у 2 рази більша за ширину, розрізають на 14 частин. З цих частин складають фігурки людей, тварин, різні предмети. Як це робиться, показано на кількох прикладах.

Спробуй скласти інші фігури.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Список  використаної і рекомендованої літератури.

1. Мартин Г. Математические новелльі . – М.; Мир, 1974.
2. Игнатьев Е. И. В царстве смекалки. – М.; Наука, 1979.
3. Лей фура В. Н. Змагання юних математиків України. – Л.; Каменяр, 2007.
4. Перельман Я. І. Жива математика. – К. ; Техніка, 1990.
5. Павлов О. Л. Математичний конкурс «Золотий ключик». – Л.; Каменяр, 2004.
6. Возняк Г. М. Позакласна робота. 5 – 7 класи. – Т.; Підручники і посібники, 1997.
7. Грицаєнко  Н. П. А ну, розв’яжи!. – К.; Радянська школа 1991.
8. Кордемський  Б. О. Математична смикала. – М. ; Наука, 1980.
9. Карнаух П. М. Цікаві завдання з математики. – Т. ; Навчальна книга – Богдан, 2005.
10. Богданович М. В. Математичні джерельця. – К. «Веселка», 1988.
11. Конфорович А. Г. Математичні софізми і парадокси. – К. «Радянська школа», 1983.
12. Сеня Я. Г. Математичні олімпіади школярів. – Р. 2002
13. Бернацька Т. В. Готуємось до математичної олімпіади. Л. 2002.