Презентація "Алгебраїчний та графічний способи розв'язання систем рівнянь з двома змінними"
Про матеріал
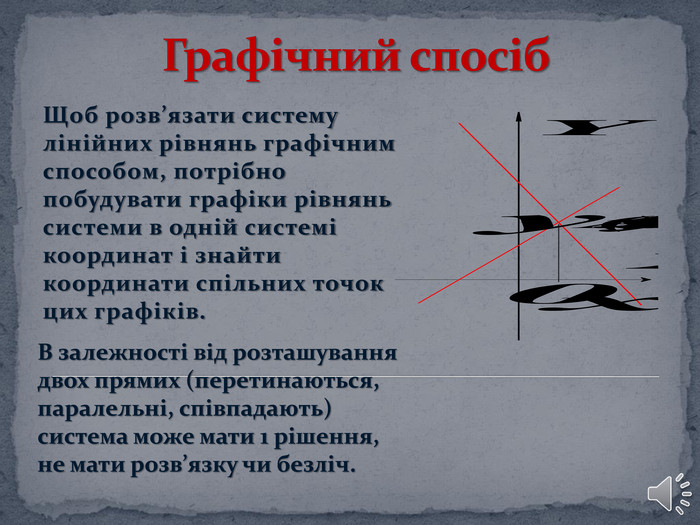
Дана презентація буде корисною для вивчення теми "Системи рівнянь з двома змінними" у 7 класі та у 8-9 класах як спосіб повторення матеріалу при підготовці до ДПА. В презентації розібрані різні види завдань. Перегляд файлу
Зміст слайдів
pptx
До підручника
Алгебра 7 клас (Мерзляк А.Г., Полонський В.Б., Якір М.С.)
До уроку
Системи рівнянь із двома змінними Оцінка розробки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку