Презентація "Числа Фібоначчі"
Про матеріал
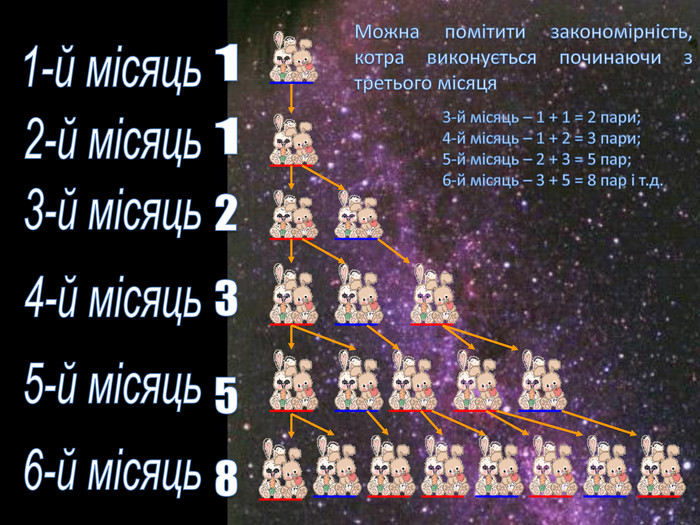
Презентація є додатком до уроку. В цій презентації учні знайомляться із новим поняттям ЧИСЕЛ ФІБОНАЧЧІ та іх використанні Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку