Презентація "Лінійні рівняння з параметрами, що задовольняють певним умовам"

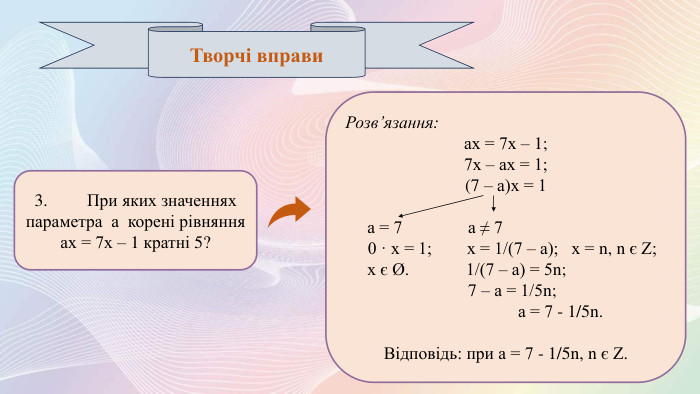
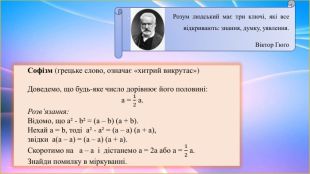
В презентації розглянуто приклади лінійних рівнянь з параметрами, що задовольняють певним умовам, методи їх розв'язування, дослідження кількості коренів рівняння в залежності від значень параметрів. Даний матеріал актуальний, оскільки вміння розв'язувати рівняння з параметрами знадобиться учням для написання ДПА і НМТ.