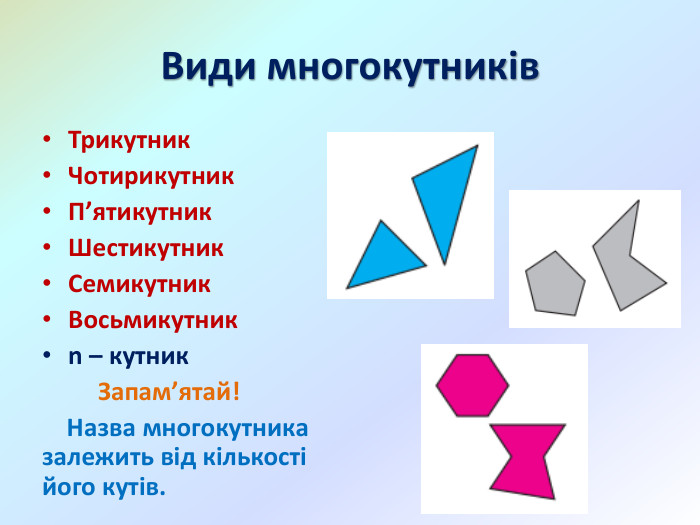
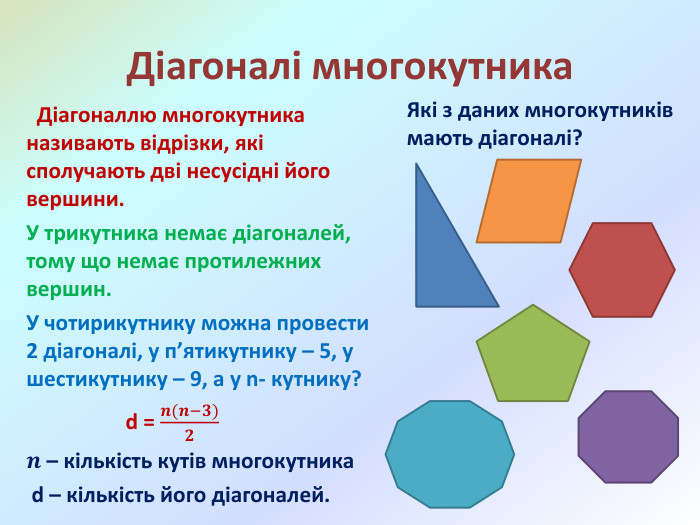
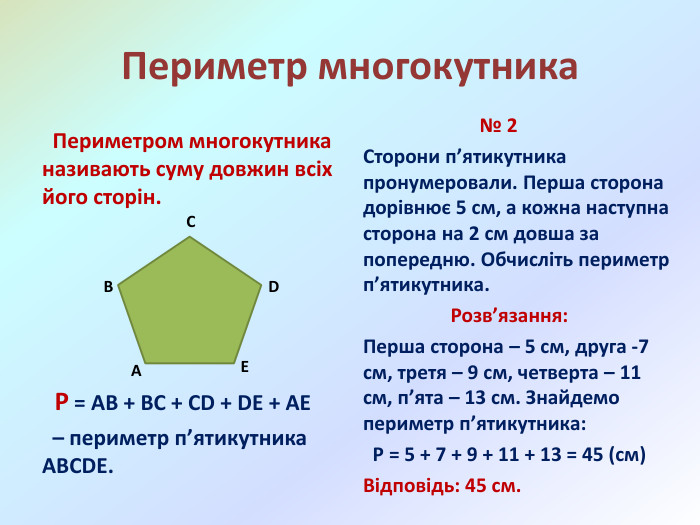
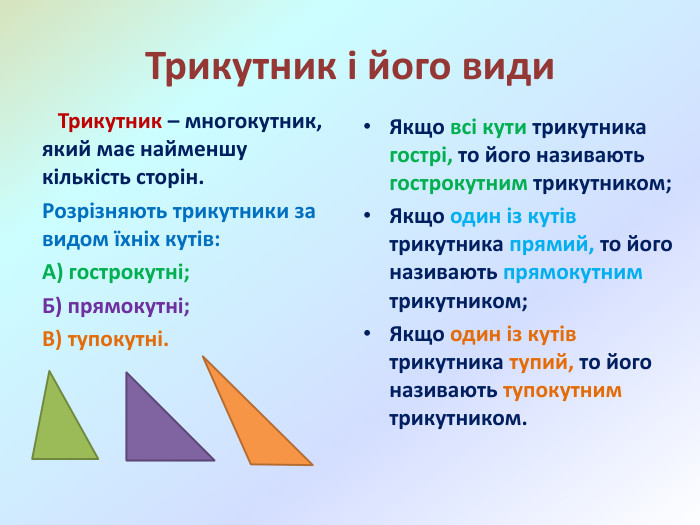
Презентація "Многокутники. Рівні фігури. Трикутники та їх види"
Про матеріал
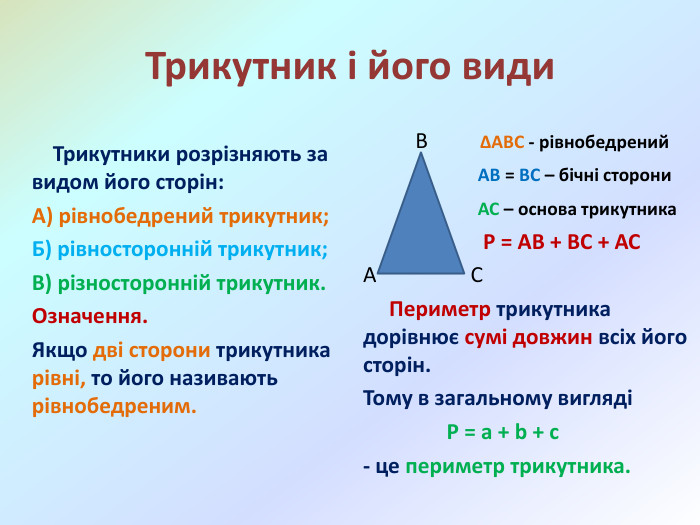
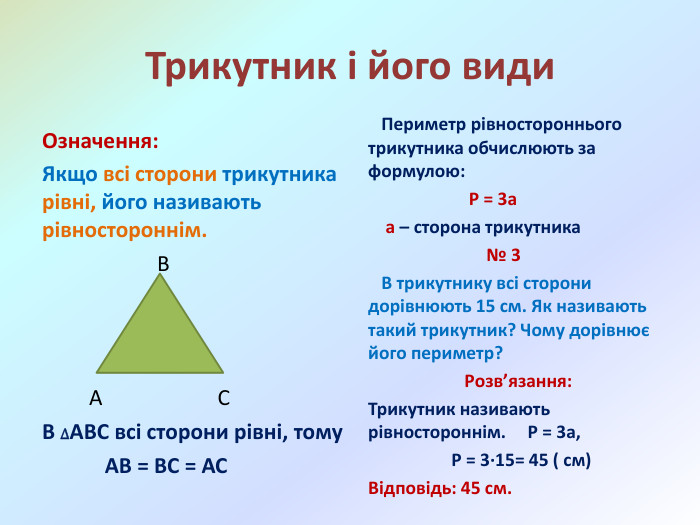
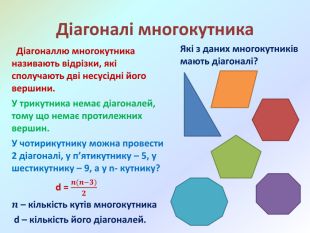
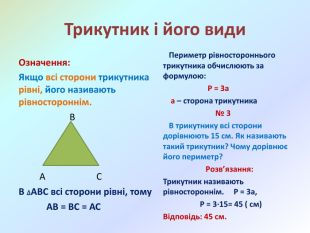
Презентація Многокутники. Рівні фігури. Трикутники та їх види" створена для проведення дистанційного уроку математики у 5 класі за програмою НУШ. Підручник "Математика" 5 клас, 2022 року.. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку