Розкладання многочленів на множники способом винесення спільного множника за дужки

Тема: Розкладання многочленів на множники способом винесення спільного множника за дужки

Мета:

Навчальна:  сформувати поняття розкладання многочлена на

                     множники; сформувати вміння розкладати многочлена на

                     множники способом винесення спільного множника за дужки;

Розвивальна: активізувати пізнавальну діяльність учнів;

                     формувати вміння  вибирати і використовувати необхідну

                     інформацію для розв’язування задач;

Виховна:     виховувати позитивне ставлення до навчання,

                    старанність, дисциплінованість.

• формувати пізнавальну компетентність (поняття розкладання многочлена на  множники);
• формування інтелектуальної компетентність (бліц-опитування );
• формування полікультурної компетентності (виховувати позитивне ставлення до навчання, старанність, дисциплінованість);
• формування комунікативної і практичної компетентностей, розвиток індивідуальних здібностей (робота з підручником).

Тип уроку: відкриття нових знань, умінь, навичок

Обладнання:  плазма, ноутбук, роздатковий матеріал

План уроку:

1. Організаційний етап. (1хв).

2. Перевірка домашнього завдання. (3хв)

3. Формування мети і завдань уроку(5хв.)

4. Актуалізація опорних знань. (5хв).

5. Засвоєння знань (27хв).

6. Підсумок  уроку. (3хв).

7. Домашнє завдання(1хв.)

Хід уроку

1.Організаційний етап

Доброго дня, діти! Як настрій? Готові до уроку? Сьогодні у нас буде дуже цікавий урок, на якому ви дізнаєтесь багато цікавої та корисної інформації для себе. Відкрийте зошити, запишіть сьогоднішнє число.

2. Перевірка домашнього завдання

3.Формування мети і завдань уроку

• Як обчислити у найзручніший спосіб вираз:  ?
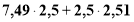• Зверніть увагу на те, що є спільного в обох доданках.
• Чи можемо ми поділити цей вираз на спільний множник?  ( Так, за розподільною властивістю) 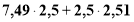= 2,5∙(7,49+2,51)=2,5∙10=25
• Як ви бачите можна розв’язати вираз простішим способом.

Тема  сьогоднішнього уроку «Розкладання многочленів на множники способом винесення спільного множника за дужки».

Отже, завдання уроку – зрозуміти, що означає розкласти многочлен на множники, засвоїти один із способів розкладання многочленів на множники: винесення спільного множника за дужки.

4. Актуалізація опорних знань

Отже, враховуючи поставлені цілі і план уроку, перейдемо до повторення теоретичних знань у вигляді бліцопитування «Вірю чи не вірю».У вас на партах лежать зелені та червоні картки. Я зачитую твердження,а ви уважно слухаєте і якщо я правильне твердження прочитала піднімаєте зелену картку,а якщо ні – червону. Щоб не заплутатись, пригадайте, на яке світло світлофора ми переходимо дорогу, а на яке стоїмо. Починаємо.

Бліцопитування

Чи вірите ви, що …

1) Одночлен – це добуток чисел, змінних і їх степенів? (так)

2) Многочлен – це сума кількох одночленів? (так)

3) Многочлен, який містить три доданки, називають кубічним многочленом? (ні)

4) Число, яке підноситься до степеня, називається основою степеня? (так)

5) Числовий множник одночлена, записаного у стандартному вигляді називається стандартний множник? (ні)

6) Третій степінь числа – це куб цього числа? (так)

7) Тотожність – це рівність, що містить невідоме? (ні)

8) Добуток кількох рівних множників – це квадрат числа? (ні)

9) Члени многочлена, що відрізняються тільки коефіцієнтами, називаються подібними членами? (так)

10) Многочлен стандартного вигляду складається з одночленів стандартного вигляду? (ні)

11) Значення невідомого, при якому рівняння перетворюється в правильну рівність, називається показником степеня? (ні)

А зараз усний рахунок

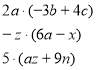
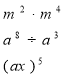
Молодці! Рухаємось далі.

5. Засвоєння знань

 Ви вже вмієте розкладати на множники натуральні числа. Наприклад,

        На множники розкладаються і многочлени.

        Розкласти многочлен на множники – це  означає замінити його добутком кількох многочленів, тотожним даному многочлену.

       Наприклад:

розкладається на такі множники (х+1) та (х-1), тому

є правильною. Одним із способів розкладання многочленів на множники – винесення спільного множника за дужки. Винести спільний множник за дужки можна, застосувавши розподільну властивість множення . Ці вирази тотожні тому правильною рівністю є

         Ця формула є записом алгоритму розкладання многочлена на множники способом винесення  спільного множника за дужки.

         Наприклад,   має спільний множник а, на підставі розподільного закону множення маємо :

Отже, многочлен ми розклали на такі множники, як а і (х+у). Ще наведемо приклади

5х+5у=5(х+у); 30+15с=15(2+с)

Іноді доводиться розкладати на множники і такі вирази, які мають спільний многочленний множник

Наприклад  

а(в-с)+х(в-с) спільний множник тут буде (в-с)

а(в-с)+х(в-с)=(в-с)(а+х). Ще цікаво знати, що один і той множник можна розкласти по-різному.

Алгоритм розкладання многочлена на множники способом винесення спільного множника за дужки.

1. Визначити спільний множник многочлена.
2. Винести спільний множник за дужки.

Робота з підручником.

№ 433 (Колективна робота.)

№435
 

№437

№441

6. Підсумки уроку

• Що ми вивчали сьогодні на уроці?
• Назвіть алгоритм розкладання многочлена на множники способом винесення спільного множника за дужки.

7.Домашнє завдання

Опрацювати §12

Розв’язати №434, №436