Розробка STREAM-уроку на тему: «Рекурсія в інформатиці і природі. Рекурсія в мистецтві.»

STREAM-урок на тему:

«Рекурсія в інформатиці і природі. Рекурсія в мистецтві.»

Розділ: Інформатика

Рівень (клас): 10 

Тип уроку: 2 по 40 хв.

Тема:  «Рекурсія в інформатиці і природі. Рекурсія в мистецтві.»

Мета:

S (наука) Інформатика: розкрити поняття «рекурсія», умови її утворення, ознайомитись з алгоритмом і задачами для опису мовою програмування рекурсії.

T (технологія): формування навичок самостійної дослідницької діяльності та вдосконалення вміння розв’язувати задачі прикладного характеру.

R (читання+письмо): акцент на розумінні змісту тексту, розвиток моторики, підготовка руки до письма.

E (інженерія): проєктування розв’язку задачі шляхом проведення експерименту.

A (мистецтво) ознайомитись з прикладами коли рекурсія зустрічається в мистецтві.

M (математика) вдосконалювати навички розв’язування задач.

Обладнання: комп’ютер, додаткові матеріали, аудіо та відео фрагменти.

Хід уроку

І. Організація учнів до уроку. Вчитель перевіряє підготовку учнів/учениць до уроку, сприяє організації уваги учнів/учениць (привітання, побажання хорошого настрою).

II. Актуалізація опорних знань. Постановка проблемного питання.

Ви коли-небудь бачили картинку в картинці? Ефект Дросте - це зображення з зменшеною версією самого себе всередині, яке, здається, триває вічно, створюючи унікальний оптичний досвід. Цифрова епоха вивела такі зображення на абсолютно новий рівень, зробивши їх чимось, з чим ми часто стикаємося. Ось докладніше про цей стиль зображень і про те, як він з'явився.

Оригінальна реклама какао Droste

Названий на честь голландського бренду какао, який використовував техніку на своїх упаковках, ефект Дросте став креативним способом художнього показу фотографій. У мистецтві він вважається прийомом зображення образу в образі - або навіть історії в історії - часто таким чином, що передбачає нескінченне повторення.

У наш час цей візуальний ефект можна зробити за допомогою цифрових маніпуляцій, а також за допомогою двох дзеркал, які відображають одне одного. Ефект Дросте продовжують використовувати бренди в логотипах.

Рис 1. Оригінальна банка для какао Droste 1904 року, розроблена Яном Міссетом (1861–1931). Фото з сайту wikipedia.org

Трикутник Серпінського - фігура, малі частини якої при довільному збільшенні є подібними до неї самої. Математичний опис такої фігури був запропонований польським математиком Вацлавом Серпінським в 1915 році. Цей трикутник є одним з найбільш ранніх прикладів так званого “фракталу” - нескінченно самоподібної геометричної фігури, кожен фрагмент якої повторюється при зменшенні масштабу, відомих з середньовіччя. 

Ми можемо бачити трикутник Серпінського на зображенні Римської мозаїки 3 — 4 століття в античному музеї міста Арль, Франція

Рис 2. Римська мозаїка. Фото з сайту wikipedia.org

Але точно ви часто бачили зображення космічних галактик чи незвичний симетричний візерунок на гілках деяких рослин, панцирах равликів чи деяких видах рослин.

Рис 3. Спіралі в природі. Фото взято з сайту https://successvector.com/

А чи задумувались ви що об’єднує всі ці зображення?? Тільки дуже схожий малюнок чи щось більше?

ІІІ. Визначення теми й мети уроку.

-                 Спробуйте визначити що об’єднує всі ці зображення? (Учні/учениці можуть помітити, що деякі зображення містять постійно повторювані фрагменти в своєму складі)

-                 Отже, сьогодні ми дізнаємося, що існує таке поняття як Рекурсія. Рекурсія (від лат. recursio – колообіг) досить поширене явище, яке зустрічається не тільки в в підручниках, а й у повсякденному житті.

IV. Зіткнення учнів з проблемою.

1. Вправа «Експеримент»

-                     Давайте спробуємо відтворити частину експерименту і спробувати отримати чи побачити рекурсію самостійно? Найпростіший спосіб побачити рекурсію - це навести Web-камеру на екран монітора комп'ютера, попередньо її включивши. Таким чином, камера буде записувати зображення екрану комп'ютера, і виводити його ж на цей екран, вийде щось на зразок замкнутого циклу. Ми будемо спостерігати щось схоже на тунель.

Рис 4. Знімок повторюваного екрану монітора. Фото автора.  

2. Вправа «Спостереження»

-                     Давайте пригадаємо, чи стояли ви колись на верхньому поверсі, вище сходів. Якщо подивитись униз, то можна побачити спірально закручувані сходи, що йдуть вниз до центру.

Рис 5. Гвинтові сходи в музеї Ватикан. Фото автора. 

3. Вправа «Творча»

-                     Давайте прочитаємо  вірш Анатолія Костецького «Вірш без кінця»

Я йду собі дорогою,
дорогою широкою,
аж тут назустріч — кіт.

— Куди ти йдеш дорогою,
дорогою широкою?—
мене питає кіт

і жде від мене слова,
а я й кажу котові:

— Я йду собі дорогою,
дорогою широкою,
аж тут назустріч — кіт.

"Куди ти йдеш дорогою,
дорогою широкою?"—
мене питає кіт

і жде від мене слова,
а я й кажу котові:

— Читай спочатку
знову!

THIS IS THE HOUSE THAT JACK BUILT

This is the house that Jack built.

 

This is the malt

That lay in the house that Jack built.

 

This is the rat,

That ate the malt

That lay in the house that Jack built.

 

This is the cat,

That killed the rat,

That ate the malt

That lay in the house that Jack built.

 

This is the dog,

That worried the cat,

That killed the rat,

That ate the malt

That lay in the house that Jack built.

 

This is the cow with the crumpled horn,

That tossed the dog,

That worried the cat,

That killed the rat,

That ate the malt

That lay in the house that Jack built.

 

This is the maiden all forlorn,

That milked the cow with the crumpled horn,

That tossed the dog,

That worried the cat,

That killed the rat,

That ate the malt

That lay in the house that Jack built.

 

This is the man all tattered and torn,

That kissed the maiden all forlorn,

That milked the cow with the crumpled horn,

That tossed the dog,

That worried the cat,

That killed the rat,

That ate the malt

That lay in the house that Jack built.

 

This is the priest all shaven and shorn,

That married the man all tattered and torn,

That kissed the maiden all forlorn,

That milked the cow with the crumpled horn,

That tossed the dog,

That worried the cat,

That killed the rat,

That ate the malt

That lay in the house that Jack built.

 

This is the cock that crowed in the morn,

That waked the priest all shaven and shorn,

That married the man all tattered and torn,

That kissed the maiden all forlorn,

That milked the cow with the crumpled horn,

That tossed the dog,

That worried the cat,

That killed the rat,

That ate the malt

That lay in the house that Jack built.

 

This is the farmer sowing his corn,

That kept the cock that crowed in the morn,

That waked the priest all shaven and shorn,

That married the man all tattered and torn,

That kissed the maiden all forlorn,

That milked the cow with the crumpled horn,

That tossed the dog,

That worried the cat,

That killed the rat,

That ate the malt

That lay in the house that Jack built.

 

V. Робота над гіпотезами, висловленими учнями.

Учні/учениці збирають та аналізують дані, необхідні для розв'язання проблеми. Вчитель виступає в ролі тьютора/фасилітатора, спонукає учнів/учениць до висунення ідей заохочувальними словами, підказками, надає диференційну допомогу.

1. Робота за науковим напрямком.

- Шановні учні/учениці! Проаналізуйте, що в побаченому привернуло вашу увагу?

Учні/учениці висловлюють свої думки і припущення.

2. Робота за технологічним напрямком

- Тепер давайте спробуємо виконати деякі вправи і спробуємо досягнувши результату зробити висновки.

Учням/ученицям пропонується виконати на аркушах із завчасно заготовленими трафаретними зображеннями малюнок: наприклад, намалювати гілку дерева, що розгалужується, або використовуючи один фрагмент, постійно повторюючи його, виконати повне зображення крижинки.

Рис 6. Фрагмент Рекурсивного дерева. Зображення з інтернету. 

Рис 7. Рекурсивна сніжинка.  Зображення з інтернету. 

3. Робота за інженерним напрямом.

-         Шановні учні/учениці, давайте спробуємо розв’язати класичну рекурсивну задачу за допомоги трьох штирів та кілець. Потрібно перекласти пірамідку з крайнього лівого штиря на крайні правий, виконуючи одні і ті самі кроки згідно схеми.

Учням/ученицям пропонується дивлячись на схему виконати декілька кроків, щоб перекласти кільця з одної пірамідки в іншу

Рис 8. Ханойська вежа Фото взято з сайту  https://dyermath.files.wordpress.com/

 

4. Робота за творчим напрямом.

-         Тепер давайте подивимось відеоролик та прослухаємо музичні композиції, в яких також реалізовано рекурсію.

Учням/ученицям пропонується, просканувавши qr-коди, прослухати фрагменти класичних музичних творів  де можна зустріти рекурсію:

- Канон "Pachelbel's Canon in D": У цьому відомому каноні Йоганна Пахельбеля, тема повторюється та розгортається на різних голосах, утворюючи складну інтеракцію між ними.

 

- "Болєро" Моріса Равеля: У цьому творі тема повторюється від початку до кінця, проте з кожним повторенням додається новий інструмент або шар, створюючи поступове наростання інтенсивності.

 

А також передивитись фрагмент відео з фрактальною графікою:

- "A Complicated Journey"  Mandelbrot Fractal Zoom. Найвідоміший фрактал Джона Бріггса.

 

5. Робота за математичним та інформатичним напрямком.

-         Припустимо, ми хочемо обчислити факторіал числа 5. Факторіал обчислюється для всіх невід’ємних чисел. Таким чином, ми будемо послідовно розкривати по одному множнику до тих пір, поки не досягнемо умови виходу з рекурсивного циклу. Умовою виходу з рекурсивного циклу в даному випадку буде досягненням останнім множником, що є факторіалом, значення нуль, тобто операція обчислення факторіала для нуля буде останньою для рекурсії. Це виглядатиме наступним чином:

5! = 5 × 4! => 

5 × 4 × 3! => 

5 × 4 × 3 × 2! => 

5 × 4 × 3 × 2 × 1! => 

5 × 4 × 3 × 2 × 1 × 0! => 

5 × 4 × 3 × 2 × 1 × 1 

 

А тепер спробуємо розв’язати цю задачу за допомоги Інформатики.

На прикладі мови програмування С++ ми розглянемо приклад використання рекурсії.

За допомогою мови програмування, наприклад С++, можливо зробити так, щоб функція зверталася сама до себе  - це і є рекурсія. 

Раніше ви вже вивчили поняття функції в С++, тепер ми можемо описати і рекурсивну функцію, знаючи, що вона може звертатись сама до себе.

Розв’яжемо раніше розглянуту задачу на знаходження факторіалу числа. Для цього застосуємо наступний фрагмент коду:

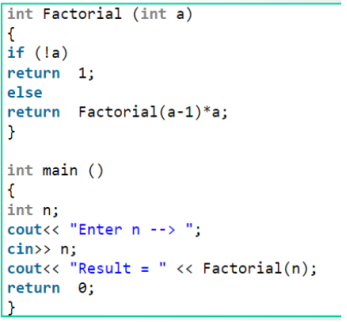
Рис 9. Фрагмент рекурсивної функції і її виклику у програмі. Фото автора.

 

VI. Загальний висновок. Учні/учениці за допомогою вчителя або самостійно формулюють висновки щодо проблемного питання, запропонованого на початку уроку (Поняття Рекурсії і використання рекурсії в різних сферах науки, мистецтва, тощо)

- Ну що ж, шановні учні/учениці! Ви старанно попрацювали, опрацювали багато матеріалів та отримали експериментальні результати. А тепер давайте пограємо у вікторину Kahoot! щоб закріпити пройдений матеріал. Приготуйте свої телефони і проскануйте qr-код. 

- Оцінювання роботи груп та окремих учнів/учениць.