Розв'язування оптимізаційних задач
РОЗВ’ЯЗУВАННЯ ОПТИМІЗАЦІЙНИХ ЗАДАЧ
Мета: формувати вміння розв’язувати оптимізаційні задачі у середовищі Wolfram|Alpha.
ПРАКТИЧНА ЧАСТИНА
Умова 1
Визначити елементи моделі оптимізаційної задачі і розв’язати її:
f(x)= x + sin x → min при 0 < = x < = 10
Хід роботи
- Визначте основні елементи оптимізаційної задачі: змінну величину, цільову функцію, критерій і обмеження.
- Відкрийте у вкладці вашого браузера https://www.wolframalpha.com.
- На головній сторінці в діалогове вікно введіть цільову функцію z і обмеження, використовуючи конструкцію
minimaze < функція> over [ <числовий проміжок>]

- Зверніть увагу на формат запису обмеження: їх потрібно записувати в формі числових проміжків у круглих або квадратних дужках, в залежності від умови.
- Запишіть розв’язок задачі: х = 0.

Умова 2
Розв’яжіть засобами СКМ Wolfram|Alpha задачу на оптимізацію:
Підприємство виготовляє 2 види фарб: для внутрішніх робіт (І) і для зовнішніх (Е). Для їх виробництва використовують сировину А і В. Максимально можливий добовий запас сировини А - 6 т, сировини В - 8 т. Добовий попит на фарбу для внутрішніх робіт перевищує попит на краску для зовнішніх робіт на 1 т, але не перевищує 2 т. Яку кількість фарби кожного виду потрібно виготовляти підприємству, щоб максимізувати прибуток від продажу, якщо ціна за 1 т фарби І - 2000 грн, фарби Е - 3000 грн?
Хід роботи
- Побудуйте математичну модель задачі. Для цього зручно представити дані задачі у вигляді таблиці (таблицю можна побудувати в текстовому редакторі):
|
Вид сировини |
Норми витрат сировини (т) на 1т фарби |
Запаси (т) |
|
|
Фарба Е (х) |
Фарба І (у) |
||
|
А |
1 |
2 |
6 |
|
В |
2 |
1 |
8 |
|
Ціна, тис грн |
3 |
2 |
|
-
Позначимо х - шуканий обсяг виробництва фарби Е, у - фарби І. Тоді цільова функція і обмеження будуть мати вигляд:
-
z = 3х + 2у
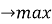
-
x + 2y
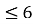
-
2x + y
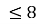
-
- x + y
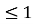
-
y
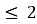
-
x
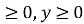
-
z = 3х + 2у
- Для розв’язання задачі відкрийте у вкладці вашого браузера https://www.wolframalpha.com.
- На головній сторінці в діалогове вікно введіть в діалогове вікно цільову функцію z і обмеження, використовуючи конструкцію
max <цільова функція> if <обмеження 1>, <обмеження 2>, ...

-
Запишіть розв’язок задачі в текстовому документі: х =
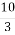 , у =
, у =  при zmax = 12
при zmax = 12 .
.
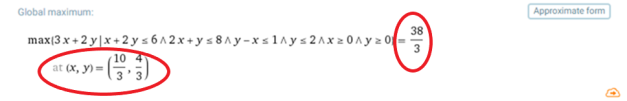
- Про виконання завдання повідомте вчителя.
Задачі для самостійного розв’язання.
Знайти екстремуми функції:
- f(x)= x 2 sin x → min при x є [0, +];
- f(x)= cox3 x + sin3 x → max при x є [-2, 1];
-
f(x)=
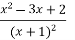 → min при x є [-2, 2];
→ min при x є [-2, 2];
-
f(x)=
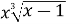 → max при x є [-7, 3].
→ max при x є [-7, 3].
Побудувати математичну модель задачі і розв’язати її:
- Для виготовлення трьох видів виробів А, В і С використовується токарне, фрезерне, зварювальне і шліфувальне обладнання. Затрати часу на обробку одного виробу для кожного з типів обладнання вказані в таблиці. У ній же вказаний загальний фонд робочого часу кожного із типів використовуваного обладнання, а також прибуток від реалізації одного виробу кожного виду. Потрібно визначити, скільки виробів і якого виду потрібно виготовити підприємству, щоб прибуток від їх реалізації був максимальним.
|
Тип обладнання |
Затрати часу (верстато-год.) на обробку одного виробу виду |
Загальний фонд робочого часу обладнання (год.) |
||
|
А |
В |
С |
||
|
Фрезерне |
2 |
4 |
5 |
120 |
|
Токарне |
1 |
8 |
6 |
280 |
|
Зварювальне |
7 |
4 |
5 |
240 |
|
Шліфувальне |
4 |
6 |
7 |
360 |
|
Прибуток (грн.) |
10 |
14 |
12 |
|
- При відгодівлі тварин кожна тварина щодня повинна одержувати не менше 60 одиниць поживної речовини А, не менше 50 одиниць речовини В і не менше 12 одиниць речовини С. Вказані поживні речовини містяться в трьох видах корму. Склад одиниць поживних речовин в 1кг кожного з видів корму наведений у таблиці.
|
Поживні речовини |
Кількість одиниць поживних речовин в 1кг корму виду |
Норми поживних речовин |
||
|
I |
II |
III |
||
|
А |
1 |
3 |
4 |
60 |
|
В |
2 |
4 |
2 |
50 |
|
С |
1 |
4 |
3 |
12 |
|
ціна 1кг корму (коп) |
9 |
12 |
10 |
|
Скласти денний раціон, що забезпечує отримання необхідної кількості поживних речовин при мінімальних грошових витратах.
-
Для виробництва двох видів виробів
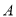 і
і 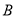 підприємство використовує три види сировини. Норми витрат сировини кожного виду на виготовлення одиниці продукції даного виду наведені в таблиці. У ній же вказаний прибуток від реалізації одного виробу кожного виду і загальна кількість сировини даного виду, яка може бути використана підприємством.
підприємство використовує три види сировини. Норми витрат сировини кожного виду на виготовлення одиниці продукції даного виду наведені в таблиці. У ній же вказаний прибуток від реалізації одного виробу кожного виду і загальна кількість сировини даного виду, яка може бути використана підприємством.
|
Вид сировини |
Норми витрат сировини (кг) на один виріб |
Загальна кількість сировини (кг) |
|
|
|
А |
В |
|
|
I |
12 |
4 |
300 |
|
II |
4 |
4 |
120 |
|
III |
3 |
12 |
252 |
|
Прибуток від реалізації одного виробу (грн.) |
30 |
40 |
|
Враховуючи, що вироби ![]() і
і ![]() можуть виготовлятися в будь-яких співвідношеннях (збут забезпечений), вимагається встановити такий план їх випуску, при якому прибуток підприємства від реалізації всіх виробів буде максимальним.
можуть виготовлятися в будь-яких співвідношеннях (збут забезпечений), вимагається встановити такий план їх випуску, при якому прибуток підприємства від реалізації всіх виробів буде максимальним.


про публікацію авторської розробки
Додати розробку
