Система уроків з математики в 5 класі по темі « Натуральні числа. Дії першого ступеня»

УРОК 1

Тема. Число. Натуральні числа. Натуральний ряд чисел і його властивості. Число нуль.

Мета: узагальнення і поглиблення знань учнів про натуральні числа. Розгляд властивостей натурального ряду чи­сел. Розвиток навичок логічного мислення учнів.

План уроку

 

І. Орієнтація

Учитель ще раз вітає учнів з початком нового навчального року, знайомить з підручником, іншими посібниками, якими вони мають користуватися: збірниками задач, дидактичними матеріалами то­що, розповідає про структуру підручника, знайомить з розділами, рубриками, параграфами тощо. Повідомляє тему і мету уроку.

 

II.  Презентація

1.Історичні відомості про натуральні числа

                 Евристична бесіда вчителя з учнями:

Натуральні числа виникли дуже давно. Число — одне з основних по­нять математики, яке дозволяє виразити результати лічби або вимірю­вання. Спочатку з'явились числа 1 і 2, трохи пізніше — 3. Комбінуючи ці числа, отримували числа до шести. А про все, що більше за шість, казали «багато». Це виражено в прислів'ях та приказках, де число 7 виступає синонімом слова «багато»: «Семеро одного не ждуть», «Сім раз відмір, один —відріж», «Один —із сошкою, а семеро —з ложкою». Згадайте й ви прислів'я та приказки, де йдеться про число 7.

Учні згадують прислів'я та приказки. Якщо учитель вважає за потрібне, таке завдання можна задати додому.

З плином часу люди навчались облічувати все більші і більші кількості. Довго вважалося, що існує якесь найбільше число. Наші пращури називали найбільше число «колода» і вважали його рівним 1096. І лише згодом люди зрозуміли, що найбільшого числа немає.

-Якщо треба порахувати кількість учнів у класі( зошитів на парті, поверхів у будинку тощо), то з якого числа починаємо лічбу?Отже, яке натуральне число є найменшим?

-Як відрізняється кожне наступне число від попереднього? А від наступного?

-Яке натуральне число передує числу 365, стоїть за числом 349?

 

2.Робота з підручником

Учитель пропонує дітям знайти в п. 1підручника  відповідь на пи­тання: «Які числа називаються натуральними?».

Отже, натуральні числа пов'язані з оточуючими нас предмета­ми. Натуральні числа показують кількість (число) предметів або порядок, в якому вони розташовані один за одним. Якщо сьогодні в класі присутні ____________ (учитель рахує) дівчаток та ___________ (учитель рахує) хлопчиків, то разом присутні ____________ (учитель рахує) учнів. А першим(ою) у журналі за списком є учень(иця) _________________ (учитель називає прізвище). Дванадцятим(тою) у списку є _________________(учитель називає прізвищі). Якщо число відповідає на питання «скільки?», то це кількісне число, а якщо на питання «який (яка) по порядку?», то це порядкове число. Запишемо перші десять натуральних чисел — одне за одним, у по­рядку зростання (один із учнів записує на дошці, інші — в зошитах).

Ви всі розумієте, що числа на цьому не закінчуються: за числом 10 йде 11, 12 і так далі, тому домовилися наприкінці ряду чисел ставити три крапки, що означає нескінченність записаного.

Знайдемо в п. 1  відповідний запис про  числовий зростаючий ряд: 1, 2, 3... Як називається такий числовий ряд? Які його властивості?

Після того як учні прочитають необхідний розділ підручника, учитель має добитися від них таких відповідей-висновків, які учні мають запам'ятати як властивості натурального ряду чисел.

1. Найменше число натурального ряду — 1, найбільшого немає.
2. Для кожного числа знайдеться таке, що більше за нього на 1.
3. Для кожного числа, крім 1, знайдеться таке, що менше за ньо­го на 1.
4. Число «нуль» не є натуральним, бо не вказує на кількість пред­метів.

Наприклад: 1,2,3,4,5,…- ряд натуральних чисел;

1,2,3.- не є рядом натуральних чисел

Слова учителя:

Ці чотири правила треба запам'ятати, бо вони будуть необхідни­ми під час розв'язування багатьох задач. Повторимо властивості на­турального ряду, розглянувши число 11. Йому передує 10, наступне за ним — 12. Числа 10, 11,12 стоять одне за одним у натуральному ряді чисел.

Натуральний ряд чисел нескінченний. Це легко довести таким прикладом. Назвіть будь-яке велике число. (Хтось з учнів має назвати вголос.) А яке число більше його на 1? (Учні називають.) Висновок: найбільшого числа немає, натуральний ряд чисел не­скінченний.

 

 

ІІІ. Практика на прикладах

Учитель наводить приклади кількісних чисел, демонструючи картки з рисунками і питаючи: «Скільки предметів на рисунку?». Діти відповідають, наприклад: 3 листочки, 5 яблук, 4 квадрати, 7 трикутників, 10 вишень, 1 груша, 2 ведмедики.

Слова учителя:

А тепер згадаємо казку, яка допоможе зрозуміти порядкові на­туральні числа (демонструються ілюстрації до казки «Ріпка»).

Учитель питає:   Учні відповідають:

Хто перший

(тримається за ріпку)?  Дід Андрушка

Хто другий?    Баба Марушка

Третя?     Онучка Гвінка

Четверта?    Собачка Фінка

П'ята?     Кішка Варварка

Шоста?    Мишка Сіроманка

Далі (якщо учитель вважає це доцільним) за такою ж схемою проводиться фронтальне опитування учнів з використанням рисунків-ілюстрацій до казки «Козенятко, яке вміло рахувати до 10».

Учитель обов'язково підводить підсумок обговореного, що має за мету закріпити поняття кількісних та порядкових чисел.

 

 

III. Керована практика

Розв'язування вправ

Учні усно розв'язують вправи з підручника та дають відповіді з місць.

 № 1°, 2°, 3°, 4°. – І рівень

№ 9.18,19. –ІІ рівень

 

Дидактична гра «Математичне лото»

Спосіб гри

1. Для гри необхідно підготувати два варіанти карток для лото загальною кількістю за числом учнів у класі.
2. Робота проводиться за варіантами.
3. Два учні (по одному від кожного варіанта) викликаються до дошки, інші працюють у зошитах.
4. Учитель зачитує питання, а учні закреслюють в картках ті клі­тинки, числа в яких, на їх думку, є відповідями на питання учителя. На кожне питання відводиться 20—25 секунд.
5. Взаємоперевірка відповідей, яка надалі буде називатися «вза­ємоперевірка в парах, звіряючись з дошкою», здійснюється таким чином. Учні, які працювали в зошитах, обмінюються своїми записами для взаємоперевірки, яка проходить одно­часно з перевіркою відповідей тих, хто працював за дошкою.
6. Максимальний бал за всі правильні відповіді — 10 (правильна відповідь на питання № 6 і 7 оцінюється у 2 бали).

Вигляд карток для гри

І варіант

1	0	999		100
	20		10	14
101	7	16		13

(Підказка для учителя: якщо учень правильно відповість на всі питання, незакресленими мають залишитися клітинки з числами 0; 14; 101.)

II варіант

98	100		7	22
	13	16		20
999	0	1	10

(Підказка для учителя: якщо учень правильно відповість на всі питання, незакресленими мають залишитися клітинки з числами 0; 98; 22.)

Питання для лото

1. Яке з чисел натурального ряду є найменшим?
2. Згадайте казку про вовка та козенят. Скільки було козенят?
3. Яке з двоцифрових чисел натурального ряду є найменшим?
4. Яке число є наступним за найбільшим двоцифровим числом?
5. Яке число передує 1000?
6. Якщо а = 15, то чому дорівнює а + 1?
7. Якщо а = 21, то чому дорівнює а – 1?
8. Яка річниця незалежності України святкується у цьому році?

(Підказка для учителя: у наведених картках для лото відпо­віддю на це запитання є число 13, яке треба замінити відповід­но до поточного року.)

 

IV. Незалежна практика

Для письмового розв'язування вправ до дошки викликаються один або декілька учнів.

 № 5, 6, 8,- І рівень

 № 21, 23,27

 

       V. Підсумок уроку

Фронтальне опитування

Опитування проводиться усно, учні відповідають з місць.

1. Якими числами користуються при лічбі предметів?
2. Чи існує найменше натуральне число? Найбільше?
3. Назвіть найбільше трицифрове число; найменше трицифрове число.
4. Якщо k означає деяке натуральне число, що не дорівнює 1, то як можна записати:

а) число, яке йому передує?

б) наступне за ним число?

5. Якщо п означає 200, то які числа означають:

а) п + 1? б) n – 1?     в) n – 10? г) п + 20?

6. Скільки всього існує одноцифрових, двоцифрових та трицифрових натуральних чисел?

 

V.  Домашнє завдання

1. Підібрати прислів'я та приказки, в яких згадується число 7 (на розсуд учителя).

 п. 1;   № 7, 9, 10- І рівень

           № 22,24,25-ІІ рівень
  

 

 

 

УРОК 2

Тема.  Нумерація натуральних чисел. Десяткова система числення.

Мета:  повторити, систематизувати і поглибити  знання  учнів про десяткову систему числення, ввести поняття класу і розряду числа; форму­вати вміння читати та записувати натуральні числа.

Обладнання: таблиця «Класи і розряди натуральних чисел»

План уроку

І. Пропедевтична практика

1.Інтерактивна вправа «Мікрофон»

1. Які числа називаються натуральними?
2. Які властивості має натуральний ряд чисел?
3. Чи належить натуральному ряду число нуль? Чому?
4. Чи є найбільше число в натуральному ряді чисел? Найменше?

 

2.Розв'язування вправ

1.Яке з наведених чисел є натуральним  і чому?

0; 234; 2/7; ; 13456; 1/3; 1.

2.Назвіть числа, між якими стоїть натуральне число : 100; 999; n.

3.Скільки натуральних чисел стоїть у натуральному ряду між числами:

35 і 55; 46 і 85; 27 і 40; 10 і 100? Як це обчислити?

4. Спробуйте встановити закономірність  у поданих рядах чисел і назвіть  наступні два числа в кожному ряду:

А) 2,4,6,8…, б)1,3,5,7….,в)1,10,100,1000….г)1,2,4,8…

 

ІІ. Орієнтація.

Вчитель повідомляє учням тему і мету уроку.

ІІІ.      Презентація

Учитель пропонує учням згадати, як називаються значки для запису натуральних чисел та скільки їх, а потім записує цифри на дошці. Учні повинні скопіювати цей запис у зошити. Доцільно роз­повісти учням матеріал історичної довідки. Свою розповідь учитель супроводжує записами на дошці або плакатами, які демонструє учням у необхідній послідовності.

 

Спосіб запису чисел називається нумерацією. У слов'янських народів колись використовувалась алфавітна нумерація. Перші дев'ять букв, над якими стояв спеціальний знак — (титло), відігра­вали роль перших дев'яти чисел. Ці дев'ять чисел зображені на рисунку (див. також [1]: форзац; [2]: с. 13).

        

Наступні дев'ять букв, позначені зверху титлом, показували десятки, а ще наступні дев'ять — сотні.

Великі числа слов'яни записували тими ж буквами, але для позначення тисяч був інший знак: .

Тобто число 1000 записували так:, а число 3000 — так:.

Число 10000 позначали: і називали «тьма».

Та нумерація, що прийнята зараз, виникла в стародавній Індії. Звідти її запозичили араби, а від арабів вона прийшла в Європу. Ця нумерація зручна: вона потребує всього 10 цифр, за допомогою яких можна записати будь-яке натуральне число. До речі, саме число залежить від місць (позицій), які займають ті чи інші цифри. Тому така нумерація отримала назву позиційної.

Але європейці познайомилися з позиційною нумерацією у XII сто­літті. До цього в Європі вживалася римська нумерація. Про неї ми поговоримо на іншому уроці.

Наступні чотири століття вживалися обидві нумерації, і тільки в XVI столітті позиційна нумерація стала в Європі загальноприй­нятою.

 

Таблиця класів і розрядів

Учитель вивішує на дошці таблицю класів і розрядів або пропо­нує учням розглянути таблицю в підручнику (посібнику), нагадую­чи, що таку таблицю діти вже вивчали в молодших класах,

 

Розв'язування вправ

Усне розв'язування вправ має за мету допомогти учням опра­цювати новий матеріал. Учні відповідають з місць.

 № 14.

Під час повторення нумерації треба показати учням, який великий мільйон.

Завдання. Обчислити, якою завтовшки була б книга в мільйон сторінок ?

(близько 50 метрів)

Мільйон людей

III.  Практика на прикладах

Розв'язування вправ

Розв'язування наведених вправ — письмове. Тому учитель викликає до дошки одного за одним декілька учнів.

 № 15, 17.

IV. Керована практика

1.Прочитайте число: а) 85369; б) 256 308; в) 103 200 ; г) 1 001 001.

2.Яке найбільше і яке найменше  чотирицифрове число можна записати за допомогою цифр 0,3,5,7, якщо кожну цифру використовувати один раз?

3.Запиши цифрами  число:

а) десять мільйонів сорок сім тисяч:

б) триста сорок п’ять мільйонів чотири тисячі шість;

в) 437 тисяч;  г) 53071 тисяча; д) 4 десятки мільйонів, 5 тисяч і 4 сотні.

V. Незалежна практика

               №,29,31,32

VІ. Підсумок уроку

Фронтальне опитування

1. Скільки ви знаєте цифр?
2. Які класи існують в позиційній системі числення?
3. Як називаються розряди, що входять до класу одиниць? до класу тисяч? мільйонів?
4. Прочитайте числа: 5835; 792. Що означає кожна цифра? (Чис­ла, запропоновані у цьому питанні, вчителю слід записати на дошці.)
5. Запишіть рік свого народження, зліва допишіть цифрами місяць і день свого народження. Прочитайте отримане число. Яка цифра в записі числа означає одиниці мільйонів? Десятки мільйонів? Чому вона не однакова у всіх або її не існує в записі числа? Чи є в записі розрядів класу тисяч такі цифри, які однакові для всіх учнів?

 

VІІ.  Домашнє завдання

п. 2; №16.26. – І рівень

№30,34,35- ІІ рівень

УРОК 3

Тема.  Класи та розряди натуральних чисел, більших ніж мільйон. Інші системи числення.

Мета: Ознайомлення з числами, більшими ніж мільйон, їх читанням і записом. Розвиток пізнавальної активності та логічного мислення при ознайомленні з матеріалом про інші системи числення та шляхом розв'язування задач і вправ.

План уроку

І. Пропедевтична практика

1.Математичний диктант

Схема проведення диктанту

1. Робота проводиться за варіантами.
2. Двоє учнів (по одному від кожного варіанта) працюють за дошкою, решта записують відповіді на запитання учителя в зошитах.
3. Здійснюється взаємоперевірка в парах, звіряючись з дошкою.
4. Зошити з диктантом учитель збирає для перевірки, після чого оцінює роботу учнів, що працювали за дошкою (максимальна оцінка — 10 балів, по 2 бали за кожне повністю правильно виконане завдання з п'яти). Під час перевірки роботи учнів, що працювали за дошкою, учитель має відповісти на запитан­ня учнів, якщо вони виникли.

Питання

І варіант  II варіант

1. Запишіть число:

а) 20 137   а) 40 215

б) 6012   б) 2049

в) 2 000 000   в) 13 000 000

г) 100 013   г) 40 200

2. Запишіть у вигляді суми розрядних доданків число:

а) 518    а) 623

б) 7203   б) 4075

3. Запишіть число, яке отримаємо із запису його у вигляді суми розрядних доданків:

а) 4000 + 200 + 10 + 3   а) 1000 + 300 + 1

б) 80000 + 500 + 9   б) 70 000 + 4000 + 40 + 9

4. Запишіть число, у якого:

а) 1 сотня 2 десятки 3 одиниці    а) 8 сотень 3 десятки 4 одиниці

б) 9 сотень 7 десятків   б) 4 сотні 5 одиниць

в) 2 тисячі 3 сотні 1 десяток       в) 5 тисяч 1 сотня 4 одиниці

5. Запишіть усі трицифрові числа, які можна утворити з даних нижче цифр, таким чином, щоб у одному числі цифри не повторювались, та знайдіть суму найменшого та найбільшо­го з них.

2; 0; 7    1; 0; 3

 

II. Орієнтація.

 Повідомлення теми і мети уроку.

ІІІ. Презентація

Для того щоб навчити учнів читати числа, більші ніж мільйон, учитель демонструє запис числа на дошці або відповідний плакат з таким записом:    567 421 028 943 426 841.

 

Щоб прочитати число, що записане в десятковій системі, його розбивають справа наліво на класи, по три цифри в кожному класі. Крайня зліва група цифр може налічувати три цифри, дві або одну. Найменший клас (останні три цифри справа) — клас одиниць, за ним, лівіше, йде клас тисяч. Є назви і для інших класів, наступних за класом тисяч: мільйони, мільярди, трильйони, квадрильйони, квінтильйони і т. д.

Читають числа зліва направо, називаючи трицифрові (двоциф­рові або одноцифрові) числа, які записані в даному класі, потім промовляють назву класу.

Учитель демонструє такий запис:

Клас мільярдів  Клас мільйонів  Клас тисяч  Клас одиниць

           604                    145                820          043

При читанні класу одиниць слово «одиниць» не проговорюють. Таким чином, число, що наведене на рисунку, читають так: шістсот чотири мільярди сто сорок п'ять мільйонів вісімсот двадцять тисяч сорок три.

 

Давайте розглянемо римську нумерацію. Ця непозиційна нумерація довгий час панувала в Європі. Навіть з того часу, як у XII сторіччі десяткова система числення потрапила до Європи, римська нумерація ще майже чотири сотні років була широко вжи­вана у європейців, проте все ж таки не змогла встояти перед більш практичною десятковою позиційною нумерацією.

Зараз всюди панує десяткова система, однак ми доволі часто зустрічаємося з римською нумерацією: наприклад, у назві школи І—ІІІ ступенів використовується запис за допомогою римських зна­ків. Ось вони. (Учитель демонструє запис деяких римських цифр і чисел та відповідних їм арабських: пише на дошці, використовує проектор.)

І	ІІ	ІІІ	ІV	V	VI	VII	VIII	IX	X
1	2	3	4	5	6	7	8	9	10
		L		C		D		M
		50		100		500		1000

 

Учитель розповідає учням правила запису римських чисел: одну й ту саму цифру більше трьох разів підряд не записують; якщо більша цифра стоїть перед меншою, то вони додаються; якщо менша цифра стоїть перед більшою, то менша відніма­ється від більшої.

Учитель наводить наступні приклади і пояснює учням, як перевести римське число в десяткове:

а) XXXII = 32;    г) ММШ = 2003;

б) DXL = 500 + 50 – 10 = 540;     д) CXLIX = 149.

в) MCMLXX = 1970;

  Римська система числення непозиційна, крім того, в ній від­сутній нуль, тому вести обчислення дуже складно. Але римська нумерація й досі збереглася для позначення століть, пам'ятних дат, ювілеїв, чисел на годинниках тощо.

Існують також інші системи числення. Наприклад, в сучасних обчислювальних машинах використовується двійкова система — одна з найдавніших систем числення, відома з IV ст. до н. є. У ній використовуються лише дві цифри: Oil. Тобто перші 10 чисел мають такий запис (учитель пише на дошці або демонструє плакат):

 

0	1	10	11	100	101	110	111	1000	1001	…
0	1	2	3	4	5	6	7	8	9	…

 

Як видно, це недесяткова позиційна система, бо від позиції цифри 0 або 1 залежить значення числа.

Найдавнішою системою числення вважається шістдесяткова, яка виникла у Стародавньому Вавилоні. Ми й досі поділяємо 1 хви­лину на 60 секунд, 1 годину на 60 хвилин.

Цікаво, що єгиптяни за 3000 років до н. є. використовували у за­пису таки знаки: для одиниць , для десятків — , для сотень —.

Наприклад, число 342 вони записували так: .

А хто може відповісти, як єгиптяни записували число 219? (Хтось з учнів має відповісти.)

Учитель пропонує учням матеріал підручника: с.16 «Хочеш знати ще         

              більше?»

 III. Практика на прикладах

 Розв'язування вправ

№60,61

 

IV. Керована практика

І рівень № 62,64

ІІ рівень №71, 73

V. Незалежна практика

Самостійна робота  (проектується через проектор на інтерактивну дошку)

Варіант 1.

1. Запишіть число: а) три мільйони чотириста тисяч; б) три мільйони чотири тисячі; в) три мільярди чотири мільйони; г) три мільярди чотириста тисяч.
2. Яке з поданих чисел є сумою найбільшого чотирицифрового числа та найменшого п’ятицифрового числа?

      а) 100 999;  б) 19 999;  в) 21 110;   г) 9 999.

3. Знайдіть серед поданих чисел таке, що є сумою всіх трицифрових чисел, у запису яких використано лише цифри 0 і 5.

а) 1 610;  б) 1 060 ;  в) 2 110  ;    г) 2 220.

 

Взаємоперевірка самостійної роботи.

 

VІ.    Підсумок уроку

Фронтальне опитування

Опитування проводиться усно, учні відповідають з місць. Завдання № 2 – 4  проектуються на дошку. Назви класів у завданні № 2 треба написати обов'язково, щоб ті з учнів, хто ще не запам'ятав їх, змогли б скористатися цією підказкою.

1. Які класи чисел ви знаєте?
2. Прочитайте записані на дошці числа.

млрд      млн тис.      одиниці

а) 729         843 999     425

б)  13          042 704     800

в)    5          003 200     101

г) 400         000 142     505

д)  20          003 800         003

3. Що означає цифра 5 у запису чисел: 25; 549; 54 005?
4. Скільки це: XX, V, VIII, X, IV, VI?

 

VII. Домашнє завдання

 п. 2, с. 14 – 16;

І рівень  № 63, 66,69

ІІ рівень № 74,76,79.

 

УРОК 4

Тема.  Додавання. Компоненти додавання. Переставна і сполучна властивості додавання.

Мета: повторення та узагальнення знань учнів про додавання натуральних чисел. Формулювання властивостей додавання, знайомство з буквеним записом цих властивостей. Формування вмінь і навичок застосування властивостей додавання.

План уроку

.

 

I. Пропедевтична практика

Вступна бесіда

Бесіда починається з фронтального опитування учнів за такими питаннями.

1. Як називаються числа, які додають?
2. Як називається результат додавання?
3. Що означає вираз: «одиниця переходить у старший розряд»?
4. Які цифри замінили зірочками, якщо додавання виконане правильно?

       

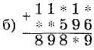
5. У записі 5555 поставте між цифрами знак «+», щоб отримати:
   а) 20;  б) 65;  в) 110; г) 560.
6. Знайдіть суму всіх одноцифрових чисел і запам'ятайте її. Як краще (зручніше) її обчислити?

(Відповідь для учителя: 0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = (0 + 9) + (1 + 8) +

+ (2 + 7) + (3 + 6) + (4 + 5) = 9 + 9 + 9 + 9 + 9 = 45.)

Учитель підводить учнів до висновку, що, якщо знаєш закони додавання, знаходити суму чисел більш зручно.

 

II. Орієнтація

Учитель пояснює учням, що знання властивостей додавання надає можливість швидко і правильно обчислювати суми — як письмово, так і усно. Повідомлення теми і мети уроку.

 

IІІ. Презентація

                               План вивчення теми

1.Приклади задач, для розв’язування яких необхідно виконати додавання чисел.

2. Додавання багатоцифрових чисел за розрядами(у стовпчик)

3. Властивість нуля при додаванні.

 

1. Учитель пропонує учням знайти суму чисел:

а) 889 + 143 + 111; б) 625 + 1240 + 375 + 760; в) 6580 + 1220 + 420.

Якщо учні виконують додавання в порядку запису, то учитель пропонує виконати додавання усно. Хто з учнів знає, як раціонально зробити додавання, той виходить до дошки і має записати:

а) 889 + 143 + 111= (889 + 111) + 143 = 1000 + 143 = 1143;

б) 625 + 1240 + 375 +760 = (625+ 375) + (1240 +760) = 1000 + 2000 = 3000;

в) 6580 +1220+ 420 = (6580 + 420) +1220 = 7000 +1220 = 8220.

Якщо ніхто з учнів не знає, як таким чином зробити додавання,

учитель має сам зробити на дошці наведені записи.

2. Учитель розповідає про формулювання та запис законів дода­вання у буквеному вигляді: a + b = b + a; (a + b) + c = a + (b + c).
3. Учитель пропонує учням розв'язати задачу.

Учора в магазин завезли тільки яблука — 240 кг, а сьогодні завезли тільки виноград — 320 кг. Скільки всього яблук завезли в магазин за два дні? Скільки всього винограду завезли в магазин за два дні?

Учні мають отримати відповідь у такому вигляді:

240 + 0 = 240 (кг) яблук;

0 + 320 = 320 (кг) винограду.

Учитель:

Запишемо відповідь цієї задачі у буквеному вигляді:

a + 0 = a; 0 + b = b.

4. У «сильному» класі доцільно розглянути суму двох чисел і один з доданків, порівнявши їх, тобто виконати таке завдання.

Який із записів завжди буде правильним?

a + b > a, a + b > a, a + b < a, a + b < a

(або a + b > b, a + b > b, a + b < b, a + b < b).

5. Після бесіди учитель робить висновок:

a + b > a, якщо b ≠ 0;

a + b ≥  a, якщо b — будь-яке число;

a + b ≤ a, якщо b = 0, a ≠ 0 або a = b = 0;

a + b < a — ніколи не справджується.

 

ІV.  Практика на прикладах

Розв'язування вправ

Розв'язуючи усні вправи, учні відповідають з місць; для розв'язування письмових вправ учитель викликає до дошки одного за одним декількох учнів.

1.  № 143,144,145 (усно); письмово № 156,157

 

V. Керована практика.

           І рівень №159,160

           ІІ рівень № 167,168,170

VI. Незалежна практика

Самостійна робота

1°. Знайдіть суму:

а) 8 300 005 796 + 83 999 095 408;  б)19247523841 + 4387689337.

2. Не використовуючи калькулятора, виконайте додавання, об­равши зручний порядок дій:

а) 1888 + 87239 + 1112;  б) 437 + 637849 + 62151.

3*. У трикутнику ABC сторона ВС менша ніж сторона АВ на 5 см, а сторона АС більша ніж сторона ВС на 3 см. Чому дорівнює периметр цього трикутника, якщо АВ = 16 см?

Учитель називає правильні відповіді а учні перевіряють  свої результати.

VIІ. Підсумок уроку

Як називаються компоненти при додаванні?

Як правильно додати числа в стовпчик?

Які властивості 0 ми вивчили?

VIІІ. Домашнє завдання

Вивчити  п.4.

І рівень №158,162

ІІ рівень №169,171,

 

УРОК 5

Тема. Додавання. Властивості суми.

Мета:  формування навичок додавання натуральних чисел з використанням законів додавання. Ознайомлення з властивостями суми. Перевірка стану засвоєння теми шляхом виконання самостійної роботи.

План уроку

 

І.   Пропедевтична практика

Для закріплення обчислювальних навиків та з метою розвитку логічного мислення доцільно розглянути такі вправи. Там де треба, учні мають пояснити хід своїх думок.

1. Визначте останню цифру результату.

1) 2743 + 849; 2)5004 + 1006; 3) 188999 + 19991; 4)100006 + 208.

2. Доведіть, не виконуючи обчислень, що дія виконана непра­вильно.

1) 2308 + 546 = 2815;  3) 18004 + 1579 = 19665;
2) 5102 + 3008 = 9200;             4) 103 + 8711 = 8999.

3. Порівняйте, не обчислюючи, та поясніть свою думку.

1) 47 + 54 і 50 + 60;  3) 572 + 16 і 500 + 10;

2) 33 + 72 і 30 + 70;  4) 211 + 146 і 300 + 200.

4. У кожному з прикладів знайдіть суму, потім розташуйте відповіді в порядку спадання. Якщо ви зробите все правильно, то отримаєте слово, яке є назвою найвищого у світі вулкана.

Л 746 + 354  Ю 540 + 360  Ь 140 + 260

А 27 + 72  Л 146 + 44   Я 188 + 112

Ь 104 + 46  Й 171 + 29   Я 117 + 3

К 36 + 64  Ь 276 + 724   Л 169 + 331

(Відповідь для учителя: Льюльяйльяка.)

 

II. Презентація

 

Розглянемо задачу. Оля з Оксанкою збирали гриби. Оля знайшла 24 опеньки і 18 підберезників, а Оксанка — 28 опеньків і 14 підберезників. Скільки грибів зібрала кожна з дівчаток?

Звісно, що всі зможуть розв'язати цю задачу і знайти від­повідь. Прошу підняти руки, хто розв'язав. (Уголос відповідають 1—3 учні.)

Проте цю задачу було вам запропоновано з іншою метою.

Давайте порівняємо кількість опеньків та кількість підберез­ників у кожної з дівчаток. Якщо опеньків Оля знайшла менше (на скільки?), то підберезників — більше (на скільки?).

Хто може пояснити, чому, хоча кожна з дівчаток зібрала різну кількість підберезників і опеньків, сума грибів у обох однакова?

Якщо діти не можуть пояснити, учитель пропонує задачу прості­шу, з меншими доданками, або іншого змісту. Наприклад: Мишко сьогодні піймав 6 карасиків та 4 коропи, а вчора — 2 карасики та 8 коропів. Який улов був у хлопчика кожного дня?

Після цього декілька учнів мають зрозуміти, до чого веде учитель. Тоді учитель пропонує дітям сформулювати властивість суми:

Якщо один із доданків збільшити, а другий зменшити на одне й те саме число, то сума не зміниться.

Щоб додати, наприклад, 18 до будь-якого числа усно, до цьо­го числа додають 20, а потім віднімають 2. Нехай треба додати 18 до 146. Доданок 18 збільшують на 2, а доданок 146 — зменшу­ють на 2. Так рахувати легше, а сума виходить та ж сама — 164:   146 + 18 = (146 – 2) + (18 + 2) = 144 + 20 = 164. (Запис учитель робить на дошці.)

 

ІІІ. Практика на прикладах

Розв'язування вправ

Відповіді при розв'язуванні усних вправ учні надають з місць, а для виконання письмових вправ учитель викликає до дошки од­ного за одним декількох учнів.

Обчислити зручним способом

158 +388 +1012+1242

273 +417 +127 +83

43 +89 +57  

2987 +1950+13+50+7000

IV . Керована практика

Обчислити зручним способом.(завдання на картках)

І рівень                                                      ІІ рівень

(146+322) +178                                            (56 +а)+14

784 +(179+116)                                              342 +(в+58)

625 + 481 +75 +219                                       805 +х+195

427+88+203+102                                            m+4563 +1837

Відповідь:

І .646; 1079;1400;820                                 ІІ. а+70; в+400; х+1000; m+6400.

          

V.  Незалежна практика.

 Самостійна робота

Варіант 1

1°. Знайдіть суму:

а) 7068907 + 5671354229; б) 1006 804 995 + 18096 914.

2. Не використовуючи калькулятора, виконайте додавання, об­равши зручний порядок дій: а) 49617 + 999 + 383; б)52681 + 4861 + 139.

3*. У трикутнику STR сторона ST дорівнює 24 см; вона на 8 см менша ніж сторона TR і на 4 см менша ніж сторона SR?. Знай­діть периметр трикутника.

Варіант 2

1°. Знайдіть суму:

а) 63 609 806 + 8611398615; б) 2077 960888 + 25063971.

2. Не використовуючи калькулятора, виконайте додавання, об­равши зручний порядок дій: а) 695 + 2305 + 57908; б)89716 + 9688 + 312.

3*. У трикутнику МКР сторона МК менша ніж сторона КР на 18 см, а сторона МР більша ніж сторона КР на 12 см. Знайдіть периметр трикутника МКР, якщо МК = 35 см.

V. Підсумок уроку

Учитель ще раз повторює з учнями закони додавання та влас­тивість суми.

 

VI. Домашнє завдання

І рівень №164,166

ІІ рівень № 173,175,190

 

 

УРОК 6

Тема.  Віднімання. Компоненти віднімання. Віднімання суми від числа і числа від суми.

Мета: сформувати поняття дії віднімання вивчення дії віднімання, компоненти віднімання. Формування навичок віднімання суми від числа і числа від суми.

План уроку

І. Пропедевтична практика

І.Математичний диктант    (проектується на дошку)

1.Яке  число  треба поставити  замість *, щоб сума 224 +*+1276 дорівнювала 2500 ?

1)100;     2) 0;            3) 50;            4)1000.

2.У якій з наведених сум вирази в дужках рівні?

1) (0+132) +(132+1)        3)(67+22) + (43+45)

2)(731+13) +(702+42)      4)  (30+40) +(75+0)

3. Яке з наведених чисел  дорівнює сумі 4м 76 см +3м 48 см?

1) 7м 76 см; 2) 7м 48см; 3)8м 24см;  4)7м 124 см.

4. Який із зазначених порядків виконання дій  є найзручнішим для обчислення  суми 83 +127 +273+417?

1) (83 +127) +(273+417)            3)  (83 +417) +(273+127)

2) (83 +273) +(127+417)            4)   (83 +127) +(417+273).

ІІ.Орієнтація.

 Дії додавання і віднімання натуральних чисел учні вже вміють виконувати з початкових класів. Сьогодні на уроці, ми пригадаємо, як називаються числа при відніманні, та як відняти від числа суму двох чисел і від суми відняти число?

IIІ.  Презентація

Задача1.На кінець І семестру у 5 класі було 11 учнів, що вчаться на достатньому рівні. Але за ІІ семестр кількість таких учнів збільшилась , і на кінець року таких стало 15 учні. На скільки  збільшилась кількість учнів 5 класу, що навчаються на достатньому рівні?

Розв’язання.

Якщо шукана кількість  учнів невідома (х), то умову задачі можна записати так: 11+ х =15. Потрібно знайти другий доданок  за відомою сумою і першим доданком. Х=15-11; х=4. і відняти від 15 число 11 –означає , що треба знайти таке х , яке б у сумі із числом 11 дало число 15.

  Після цього учні можуть сформулювати правило:

Відняти від числа а число в –означає знайти таке число х , яке б у сумі з в давало число а:         а- в = х,    х+ в = а,

При цьому  а- зменшуване; в-  від’ємник; х-різниця.

 

Задача 2. В універмазі було виставлено на продаж 48 телевізорів, 21 музичний центр, 16 відеомагнітофонів. До обіду було продано 24 телевізори, 18 музичних центрів, 12 відео­магнітофонів. На кінець робочого дня залишилось 4 телевізори, 1 музичний центр і 1 відеомагнітофон. Скільки одиниць кожного з електротоварів було продано після обіду?

Учитель пропонує розв'язати кожному ряду (або розбиває клас на три групи) свою міні-задачу — про один із трьох електротоварів, наголошуючи, що треба продумати два різних способи отримання відповіді. Біля дошки працюють два або три учні, решта пишуть у зошитах.

Зразки записів

Телевізори

1) 48 – 24 = 24 телевізори залишилося перед обідом.

2) 24 – 4 = 20 телевізорів продано після обіду.

Або: (48 – 24) – 4 = 48 – (24 + 4) = 48 – 28 = 20.

Музичні центри

1) 21 – 18 = 3 музичних центри залишилося перед обідом.

2) 3 – 1 = 2 музичних центри продано після обіду.

Або: (21 – 18) – 1 = 21 – (18 + 1) = 21 – 19 = 2.

Відеомагнітофони

1) 16 – 12 = 4 відеомагнітофони залишилося перед обідом.

2) 4 – 1 = 3 відеомагнітофони продано після обіду.

Або: (16 – 12) – 1 = 16 – (12 + 1) = 16 – 13 = 3.

Учитель:

У кожному з виразів ми врешті-решт від числа віднімали суму. Наприклад, у випадку з телевізорами ми мали таке.

(Учитель зосереджує увагу на такому записі:

(48 – 24) – 4 = 48 – (24 + 4) = 48 – 28 = 20.)

Після цього учитель наводить ще такі приклади:

745 – (245 + 10) = (745 – 245) – 10 = 500 – 10 = 490;

576 – (16 + 276) = (576 – 276) – 16 = 300 – 16 = 284.

Учитель:

Давайте за допомогою наступної задачі ретельно розглянемо, як відняти число від суми.

Задача 3.На столі лежали 4 яблука і 2 груші. Павлик взяв собі 1 яблуко, а потім Оля взяла 1 грушу. Скільки фруктів залишилося?

Учитель пише на дошці, учні копіюють його записи в зошитах. (Записи на дошці та в зошитах бажано зробити кольоровими: яблу­ка — зеленим, груші — жовтим; можна замінити груші на сливи та зробити відповідний запис синім кольором. Відповідь слід записати білим на дошці та чорним — у зошитах.)

1) (4 + 2) – 1 = (4 – 1) + 2 = 3 + 2 = 5 (фруктів) (Павлик).

2) (3 + 2) – 1 = (2 – 1) + 3 = 1 + 3 = 4(фрукти) (Оля).

Далі учитель разом з учнями узагальнює задачу, пояснюючи випадок, коли доданки не розділені за змістом, а є просто доданками:

(625 + 143) – 125 = (625 – 125) + 143 = 500 + 143 = 643.

Або:

(625 + 143) – 125 = (143 – 125) + 625 = 18 + 625 = 643 — незручно!

(116 + 72) – 96 = (116 – 96) +72 = 20 + 72 = 92.

 

III. Практика на прикладах

Тренувальні вправи

Відповіді при виконанні усних вправ учні надають з місць, а для виконання письмових учитель викликає до дошки одного за одним декількох учнів.

  1. Усно : № 195, 196,197. 

2. Письмово: І рівень №206,207,210

                        ІІ рівень  №239,240

 

IV. Керована практика

І рівень № 211,212

ІІ рівень №242,243.

V. Незалежна практика

І рівень.

1.Що означає відняти :1) від 19 число 6; 2) число 7 від 16?

2.На скільки число 63 більше від 38?

3) На скільки 45 менше за 64?

4) На яке число  треба зменшити число 24; 38;1;0,щоб отримати 1) нуль,2) ці самі числа.

ІІ рівень

1.Обчислити:

1) 428-(128+126); 2) (428-128) – 126 ;   3)( 428-126)-128; 4) (619 +282) -219;

5) ) (619  -219) +282;  6) ) (282 – 219) +619

Порівняйте  відповіді  у прикладах 1 і2, 3 ,4,5 і 6. Що ви помітили?

2.Задача.

    Від мотузки завдовжки 200 м відрізали 3 шматки. Упер­ше відрізали 28 м, удруге — на 15 м більше, ніж уперше, а втретє — на 17 м менше, ніж удруге. Якою є довжина решти мотузки?

 

 

VІ.   Підсумок уроку

Учитель проводить фронтальне опитування щодо знаходження компонентів віднімання. Далі він пропонує пояснити наведений запис і відповісти, яке повинне бути с у порівнянні з а і b.

(a + b) – c = (a – c) + b = (b – c) + a.

Далі учитель наводить ще один запис і запитує, які повинні бути b і с у порівнянні з a:

 a – (b + c) = (a – b) – c = (a – c) – b

Усні вправи

1 Обчисліть: 28-(18+3); 45-(35+7);(88+17)-28;(79+14)-14

2.Спростіть вираз : 28-(18+а);  45-(35+в); (88+х)-28; (у+14)-14.

 

VІІ.   Домашнє завдання

П.5

І рівень 208,209,213

ІІ рівень 241,244,248

УРОК 7

Тема:  Віднімання. Додавання та віднімання різниці. Віднімання числа від різниці.

Мета: Систематизація і поглиблення знань учнів з даної теми. Розгляд способів додавання і віднімання різниці чисел.

План уроку

 

І.   Пропедевтична практика

1.Учитель пропонує дітям перевірити свої результати виконан­ня домашнього завдання, звіряючись з готовими розв'язками (їх учитель заздалегідь пише на дошці або використовує кодоплівку чи плакат).

Підбивається стислий підсумок результатів, звертається увага на моменти, які потребують підвищеної уваги (завдання, з якими не впоралася не менш ніж третина учнів).

2.  Самостійна робота 

Варіант 1(достатній та високий рівень)

1. Знайдіть різницю: 5 004 026 301 – 4 937 848 916.

2. Знайдіть значення виразу, використовуючи властивості відні­мання:

а) (357 + 289) – 157; г) 876 – (398 + 476);

б) (863 + 471) – 371; д) 529 – (229 – 103);

в) 643 – (243 + 398); є) 7382 + 1618 – 1382.

3. Виконайте дії: (3 875 674 + 2 348 754) – 2 875 674.

4. За 3 години автомобіль проїхав 163 км. За першу годину він проїхав 65 км, а за другу — на 17 км менше, ніж за першу. Скільки кілометрів проїхав автомобіль за третю годину?

Варіант ІІ(середній рівень)

1. Обчисли

367 +633

65- (29+25)

(200+31)-100   (400+59)-200

262-  13-  50         484-  24 -  60

2.У шостому класі навчається 17 хлопчиків,що на 5 більше , ніж дівчаток. Скільки учнів у цьому класі?

 

 

II.   Керована практика

1.Розв'язування усних вправ

1.Як   зміниться різниця 245-132. якщо а) зменшуване збільшити на 25;     

 б) зменшуване зменшити на 13.

2.Як зміниться різниця 396-193 , якщо від’ємник :

а) збільшити на 7; б) зменшити на 13?

    Відповіді учні надають з місць.

Учитель  звертаючи увагу на правила:

a + (b – c) = (a + b) – c = (a – c) + b.

 

2.Тренувальні вправи

       І рівень

1. Знайдіть різницю:7 002 065 440 – 6 919 278 416;

                                   8 127 345 602 – 324 857 809

2. Знайдіть значення виразу, використовуючи властивості відні­мання:

а) (2593 + 1389) – 1593;  г) 9543 – (3989 + 1543);

б) (4597 + 3899) – 1899;  д) 742 – (242 – 125);

       в) 3697 – (2697 + 899);  є) 5124 + 4318 – 3124.

ІІ рівень

1. Виконайте дії: 6 574 328 – (2 574 328 + 2 697 849).

                    7837 247 – (3 594 789 + 2 837 247).

 

2. Дошку розрізали на 3 частини. Довжина першої частини 57 см, друга частина коротша за першу на 18 см і довша за третю на 10 см. Якою була довжина дошки?

ІІІ .Незалежна практика

Робота з підручником

І рівень №215,218,219

ІІ рівень №245,246,247

ІV.   Підсумок уроку

Учитель підводить підсумок уроку, звертаючи увагу на правила:

a + (b – c) = (a + b) – c = (a – c) + b.

V. Домашнє завдання

Принести, планшети, фломастери

І рівень  № 222,223.224

ІІ рівень №250,252,253

 

 

 

УРОК 8

Тема: Розв’язування вправ

Мета:  закріпити засвоєння учнями вміння застосовувати закони додавання та віднімання натуральних чисел;розвиток логічного мислення.

План уроку

 

I. Пропедевтична практика

 

1.Дидактична гра «Бліцтурнір»

Спосіб гри

1. Для гри необхідні планшети, маркери або фломастери (на попередньому уроці учитель дав завдання учням принести їх).
2. Завдання для гри учитель має заздалегідь написати на дошці (або підготувати плакати чи кодоплівку).
3. Учитель зачитує (або показує) питання, відповіді на які учні пи­шуть на планшетах. На кожну відповідь відводиться 10 секунд.
4. Перевірка правильності кожної відповіді здійснюється одразу. Перші з правильно наданих відповідей учитель фіксує, після чого учні стирають записи губкою або серветкою і готуються до наступного питання.
5. Учитель підводить підсумок гри, визначаючи переможця, і про­сить декількох учнів прокоментувати ті питання, що викликали труднощі, і відповіді на них.
6. Оцінки за гру виставляються за бажанням учителя.

 

Питання для гри

1. Які два числа необхідно додати до 18, щоб отримати 20?
2. Які два числа необхідно відняти від 42, щоб отримати 40?
3. Обчисліть:

1) 2 + 13 +2 8 + 7;  4) 20 + 10 + 50;

2) 21 + 5 + 9 +26;  5) 60 + 30 + 40;

3) 4 +2 3 + 6 +1 7;  6) 80 + 20 + 50.

4. Назвіть число, що записане як сума розрядних доданків:
   1. 4000000000 + 6000000 + 2000 + 1;
   2. 8000000 + 300000 + 4000 + 900;
   3. 500000 + 7000 + 600 +1.
5. Запишіть число, в якому:

1) 3 десятки і 2 одиниці;        3) 3 сотні й 7 десятків;

2) 2 десятки й 3 одиниці;        4) 7 сотень і 3 одиниці.

6. У кожній парі записів є однакові числа. Знайдіть їх.

1) 400 + 60 + 3 і 64 + 3;

2) 4100 + 3 · 10 + 6 і 400 + 30 + 6;

3) 1000 · 4 + 100 · 4 + 10 · 3 + 6 і 1436;

4) 6 · 1000 + 3 · 10 + 4 і 6000 + 300 + 4.

 

II Керована практика

 

Завдання № 1. Обчисліть за наведеним зразком.

Зразок:         126 + 36 = (126 + 40) – 4 = 166 – 4 = 162.

І варіант:     242 + 39; 513 + 29; 1456 + 28;

IIваріант:    573 + 27; 714 + 59; 676 + 98;

III варіант:  808 + 56; 302 + 79; 1207 + 39.

Перед виконанням завдання № 2 учитель викликає до дошки двох учнів, які мають заповнити пропуски у наведених нижче двох завданнях-прикладах, супроводжуючи свої записи коментарями.

1) 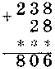                           2)

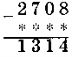
Для розв'язування завдання № 2 до дошки викликаються три учні (по одному від кожного варіанта), інші учні пишуть у зошитах.

 

 

Завдання № 2. Заповніть пропуски.

I варіант: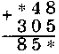     

 

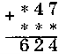
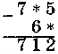
II варіант: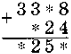    

 

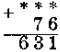
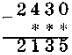
III варіант: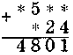    

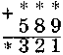
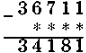
Завдання 3.За три дні в магазині було продано 219 кг апельсинів.За перший  день було продано 85 кг,що на 19 кг більше, ніж за другий. Скільки апельсинів було продано третього дня ? В який день було продано найбільше апельсинів?

Завдання 4.

Обчисли значення виразу:

234 112 +34 567-134012;

7 000 789-4 234-13 000 189

 

IІІ. Незалежна практика

І рівень.

Учні одержують кросворд з теми  «Додавання та віднімання натуральних чисел».

По вертикалі:

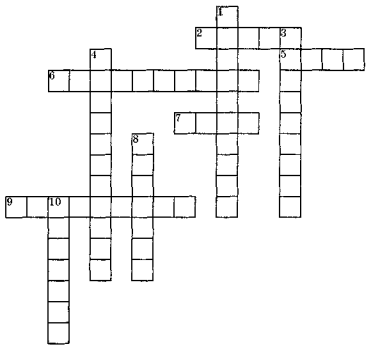1. Дія, за допомогою якої з'ясовують, на скільки одне число менше або більше за інше.

3. Назва закону додавання для кількох чисел.

4. Назва закону додавання для двох чисел.

8. Результат дії віднімання.

10. Число при дії додавання.

По горизонталі:

2. Знак, який використовують при записі дії віднімання.

5. Знак, який використовують при записі дії додавання.

6. Компонент дії віднімання, який записують на першому місці.

7. Результат дії додавання.

9. Дія, за допомогою якої знаходять загальну масу будь-чого.

 

 

 

   ІІ рівень. Гра «Хто швидше?»

1. Виконайте дії:  а) 16375 + 390332; б) 826 235 – 48081.

2. Обчисліть, на скільки число 29 714:

а) більше від 27 308;   б) менше від 39 767.

3. Обчисліть:

а) 5см 7мм + 7см 5мм ;   в) 725кг 127г + 1кг 923г;

б) 35га 8а – 14га 9а;   г) 5м 41см – 2м 79см.
4. Обчисліть зручним способом:

а) 8375 + 9625 – 6909;   б) 741 – (341 + 216).

5*. До будівельного майданчику привезли 340 т щебеню, що на 81 т більше, ніж піску, і на 103 т менше, ніж цементу. Скільки всього привезли будівельних матеріалів?

 

 V.  Домашнє завдання

І рівень.Самостійна робота №2 В-т І

ІІ рівень. Самостійна робота №2 В-т ІІІ ст..48

 

 

 

УРОК 9

Тема:   Самостійна робота  №1

Мета: Систематизація і поглиблення знань учнів шляхом розв'язування задач. Перевірка якості засвоєння основних моментів теми шляхом проведення само­стійної роботи. Розвиток логічного мислення, набуття навичок швидкої усної лічби.

План уроку

І.   Пропедевтична практика

 

Учитель поділяє клас на три групи-варіанти (для одної парти — різні варіанти) для проведення усної лічби. На дошці (кодоплівці) послідовно демонструються завдання для кожного варіанта. Учи­тель зачитує (або показує) питання, відповіді на які учні пишуть на планшетах. На кожну відповідь відводиться 10 секунд. Результати лічби учитель підводить як за варіантами, так і в цілому по класу.

І варіант               II варіант             III варіант

1) 353 + 745 + 647  1) 452 + 867-352       1) 436 + 671 + 563

2) 2427 + 641 – 427     2) 186 + 271 + 814       2) 3024 + 161 – 1024

3) 1208 – 495 + 792     3) 1663 – 278 + 337     3) 892 – 199 + 108

4) 6217 – 549 – 451   4) 8127 – 361 – 639     4) 2188 – 198 – 802

5) 83 + 49 + 51 + 17      5) 69 + 28 + 31 + 72      5) 49 + 68 + 51 + 32

 

IІ. Самостійна робота № 1

Варіант 1

1°. Виконайте дії:  а) 32 749 + 780 664; б) 286325 – 96162.

2°. Обчисліть, на скільки число 59 428:

а) більше від 54 609; б) менше від 79 529.

3. Обчисліть:

а) 14 см 8 мм + 3 см 9 мм;         в) 325 км 160 м + 24 км 875 м;

б) 5 кг 327 г + 14 кг 873 г;        г) 15 грн 3 к. – 2 грн 40 к.

4. Обчисліть зручним способом:

а) 274 + 1537 + 463;   б) 756 – (356 + 235).

5*. В одній школі навчається 518 дітей, у другій — на 64 менше, а в третій стільки дітей, скільки в першій та в другій школах разом. Скільки всього дітей навчається в цих школах?

 

Варіант 2

1°. Виконайте дії:  а) 499654 + 80261; б) 178214 – 94153.

2°. Обчисліть, на скільки число 48 234:

а) більше від 42 627; б) менше від 58 974.

3. Обчисліть:

а) 15грн 43к. + 21грн 78к.;      б) 36га 8а – 11га 9а;

в) 15т 6ц + 24т 8ц;   г) 3м 7см – 1м 41см.

4. Обчисліть зручним способом:

а) 241 + 2427 + 373;   б) (654 + 289) – 454.

5*. До магазину завезли фрукти: яблук 438 кг, груш — на 69 кг менше, а слив стільки, скільки яблук і груш разом. Скільки всього фруктів завезли до магазину?

 

Варіант 3

1°. Виконайте дії:  а) 294 732 + 40131; б) 854119 – 47254.

2°. Обчисліть, на скільки число 96 468:

а) більше від 85 254; б) менше від 116 948.

3. Обчисліть:

а) 4м 16см + 1м 89см;   в) 70 км 600 м – 2км 875 м;

б) 12т 8ц + 14т 6ц;   г) 1т 370кг – 890кг.
4. Обчисліть зручним способом:

а) 4105 + 2895 – 4937;   б) 849 – (249 + 176).

5*. В овочесховищі було 313 т картоплі. У понеділок привезли на 176 т більше, ніж було в овочесховищі, а у вівторок — на 43 т менше, ніж привезли в понеділок. Скільки тонн картоплі ста­ло в овочесховищі?

 

 

ІІІ.   Підсумок уроку

Учитель підбиває стислі підсумки, попереджає учнів, що на наступному уроці їм доведеться виконувати тематичну контрольну роботу, звертає увагу на виконання домашнього завдання, бо завдан­ня саме такого типу будуть запропоновані на контрольній роботі.

 

ІV. Домашнє завдання

Типові вправи-  ІІ рівень. ст..51

           Тестові завдання –І рівень

 

 

 

УРОК 10

Тема: Тематична контрольна робота № 1.

Додавання й віднімання натуральних чисел та їх властивості.

Мета уроку: перевірити рівень засвоєння теми  « Додавання й віднімання натуральних чисел та їх властивості»

Обладнання. картки

                                                   План уроку

 І. Організаційний момент.

Учні одержують зошити для тематичного контролю знань , записують дату .Вчитель роздає індивідуальні карточки з завданнями для контрольної роботи

                                        

ІІ. Виконання контрольної роботи

Варіант 1

1°. Виконайте дії:

а) 499654 + 80261;  б) 178214 – 94153;  в) 241 + 2427 + 373.

2°. Розв'яжіть рівняння: а) 36 – х = 29; б) х – 24 = 49.

3°. Знайдіть значення виразу (841+ х) – 425, якщо х = 725.

4.Обчисліть, обираючи зруч­ний порядок дій:

а) (324 + 546) – 124;  в) 1587 + 123 + 2413;

б) (841 + 529) – 429;  г) 449 – (49 – 18).

5. У ящику було 45 кг яблук. Після того як узяли частину яблук, у ящику залишилося 24 кг яблук. Скільки кілограмів яблук узяли з ящика?

6. Розв'яжіть рівняння 34 + (х – 10) = 39 і 84 – (у – 17) = 81. Знай­діть суму коренів цих рівнянь.

7*. На трьох ділянках посадили 126 кущів смородини. На першій і другій ділянках посадили 87 кущів, а на першій і третій — 68 кущів. Скільки кущів смородини посадили на кожній ді­лянці?

 

Варіант 2

1°. Виконайте дії:

а) 32749 + 780664;  б) 286325 – 96162;  в) 274 + 1537 + 463.

2°. Розв'яжіть рівняння: а) 27 – х = 18; б) х – 13 = 38.

3°. Знайдіть значення виразу (249 + х) – 617, якщо х = 1817.

4. Обчисліть, обираючи зруч­ний порядок дій:

а) (641 + 459) – 359;  в) 287 – (87 – 54);

б) 4127 + 1373 + 5873;  г) (1236 + 954) – 236.

5. У першій половині дня маляри пофарбували 18 м² даху. На­прикінці дня виявилося, що за день було пофарбовано 39 м² даху. Скільки квадратних метрів даху пофарбували маляри в другій половині дня?

6. Розв'яжіть рівняння 48 + (х – 21) = 68 і 96 – (у – 19) = 86. Знай­діть суму коренів цих рівнянь.

7*. Із трьох ділянок зібрали 667т зерна. З першої та другої ділянок зібрали 352т, а з другої та третьої — 454т. Скільки тонн зерна зібрали від кожної ділянки?

 

Варіант 3

1°. Виконайте дії:

а) 588 761 + 40 319;  б) 954 749 – 87 124;  в) 684 + 529 + 216.

2°. Розв'яжіть рівняння: а) 54 – х = 38; б) х – 17 = 26.

3°. Знайдіть значення виразу (1261+ х) – 785, якщо х = 1085.

4. Не використовуючи калькулятора, обчисліть, обираючи зруч­ний порядок дій:

а) (1873 + 1227) – 873;  в) 641 – (141 – 98);

б) 5124 + 676 + 4876;  г) (797 + 512) – 112.

5. На залізничну станцію прийшов поїзд із 97 товарних вагонів. Після того як частину вагонів відчепили, залишилося 48 ва­гонів. Скільки вагонів відчепили?

6. Розв'яжіть рівняння 27 + (х – 41) = 52 і 87 – (у – 25) = 83. Знай­діть суму коренів цих рівнянь.

7*. У трьох п'ятих класах 100 учнів. У 5-А і 5-Б 65 учнів, а в 5-А і 5-В – 66. Скільки учнів у кожному з класів?

 

Варіант 4

1°. Виконайте дії:

а) 724 564 + 90 737;  б) 843 524 – 29 846;  в) 392 + 474 + 626.

2°. Розв'яжіть рівняння: а) 83 – х = 45; б) х – 18 = 74.

3°. Знайдіть значення виразу (2526 + х) – 287, якщо х = 887.

4. Не використовуючи калькулятора, обчисліть, обираючи зручний порядок дій:

а) (7122 + 678) – 122;  в) (129 + 741) – 441;

б) 993 – (693 – 108);  г) 1271 + 549 + 2729.

5. На складі зберігалося 127 ящиків із фруктами. Після того як привезли ще партію ящиків із фруктами, на складі всього стало 173 ящики. Скільки ящиків із фруктами привезли на склад?

6. Розв'яжіть рівняння 63 + (х – 29) = 75 і 74 – (у – 18) = 63. Знайдіть суму коренів цих рівнянь.

7*. За три дні було скошено траву на лузі площею 35га. За перший і другий день було скошено траву на площі 22га, а за другий і третій — на площі 25га. Скільки гектарів лугу скошували кожного дня?

 

ІІІ. Домашнє завдання.

Повторити п.1-5.

Взяти канцелярське приладдя.