Стаття "Ігрові методики на уроках математики"
Ігрові методики навчання на уроках математики.
Гру, як метод, передавання досвіду старших поколінь молодшим люди використовували дуже давно. Сучасна дидактика, звертаючись до ігрових форм навчання на уроках, справедливо вбачає в них можливості ефективної взаємодії педагога та учнів, продуктивної форми їх спілкування з наявними елементами змагання, безпосередності, природного інтересу. А.Макаренко називав гру усвідомленою діяльністю, а радість гри – “радістю творчою”, “радістю перемоги”.
Якщо спочатку учень зацікавиться лише грою, то дуже швидко його вже цікавитиме пов’язаний з нею матеріал, в нього виникне потреба вивчити, зрозуміти, запам’ятати цей матеріал, тобто він почне готуватися до участі в грі. Гра дає змогу легко привернути увагу й тривалий час підтримувати в учнів інтерес до тих важливих і складних предметів, властивостей і явищ, на яких у звичайних умовах зосередити увагу не завжди вдається. Гра – це активне навчання. Систематичне використання ігор підвищує ефективність навчання. У дидактичних іграх діти спостерігають, порівнюють, класифікують предмети за певними ознаками, виконують аналіз й синтез, абстрагуються від несуттєвих ознак, роблять узагальнення. Багато ігор вимагають уміння висловлювати свою думку в зв’язній і зрозумілій формі, використовуючи математичну термінологію.
У сучасній школі, що акцентує увагу на активі-зації й інтенсифікації навчального процесу, ігрова діяльність використовується як:
• самостійні технології для опанування поняття, теми й навіть розділу навчаль-ного предмета;
• елементи більшої технології;
• урок або його частина;
• технології позакласної роботи.
На відміну від ігор узагалі, педагогічна гра має важливу ознаку – чітко поставлена мета навчання й відповідно до неї педагогічний результат, що мо-жуть бути обґрунтовані, визначені в очевидному вигляді й характеризуються навчально-пізнавальною спрямованістю. Ігрова форма занять створюється на уроках за допомогою ігрових прийомів і ситуацій, що є засобом спонукання, стимулювання учнів до навчальної діяльності. Наведу деякі приклади вико-ристання мною ігрових ситуацій на уроках математики. Описані нижче прийоми допомагають урізноманітнити форми опитування.
«Кубики». Це звичайні кубики з дитячого набору, на гранях яких знаходяться завдання ( функції, графіки, формули тощо ). Учень бере кубик, кидає його на стіл і відповідає «по зображенню», що опинилось на верхній грані, потім операція повторюється і т.д. Щоб простіше було слідкувати за відповідями, зручно фіксувати результат на дитячих рахівницях ( кожна позитивна відповідь відмічається пересуванням кульки ).
«Хрестики-нулики». Учневі дається завдання у вигляді таблиці з вихідними конкретними параметрами у стовбцях та рядках. В клітинках на перетині горизонталі та вертикалі проставляється «+» , якщо дані у стовбці та рядку відповідають одне одному, і «0» - якщо не відповідають. Завдання готується або на великому ватмані, або пишеться на відкидній дошці.
«Дерево». На дошці або таблиці зображується дерево – ялинка. На її стовбурі пишу назву теми, наприклад, «Квадратні рівняння». Учні по черзі виходять до дошки і пишуть на гілках назви основних понять, що входять до цієї теми та повісити відповідні ялинкові іграшки – це означає намалювати ялинкові кульки, прикрашені відповідними формулами.
«Квітка». На дошці малюється зображення квітки. В центрі квітки пишу тему. Учень або група учнів у пелюстках квітки повинні написати формули, що відносяться до даного поняття.
Гра «Математичне лото». На магнітній дошці розташовані хаотично картки-лото з питаннями і відповідями. Ви повинні вказати, як правильно:
Розмістити картки, щоб на дошці сформувався план розв’язування задачі і ланцюжок формул, які будуть використані вами для розв’язання задач.
Так на уроці з теми «Властивості функції.» застосовую гру «Математичне лото». Для кожної команди заздалегідь приготувала по два цупкі листи паперу. На одному з них і тільки з одного боку був кольоровий малюнок. Ці листи розділені на 25 рівних частин. На одному листі (основі) кожна частинка нумерується, і у ній записується завдання, а на другому листі ( з малюнком) на чистій стороні – відповідно відповіді до цих завдань. Цей другий лист розрізається на прямокутники, фрагменти малюнка змішуються, формується 5 пакетів по 5 карток у кожному. Для кожної команди приготували ще третій цупкий лист паперу. Кожний пакет і картки у ньому мають свій порядковий номер. Гра відбувається у два тури. І тур- теоретичний (відбірковий).У ньому беруть участь всі учні класу. Задаю запитання, учень який перший відповів правильно стає учасником ІІ тура. Таким чином набирається 4 команди по 5 учнів у кожній. Решта учнів стають помічниками учителя, з них обов’язково вибирають ведучого, спостерігачів та експертів. ІІ тур – практичний (гра). Ведучий читає одне з 25 завдань другого туру. Команди уважно слухають, при потребі письмово розв’язують це завдання. Відповідь міститься на картці в одного із членів кожної команди. Тоді цю кратку повинно покласти на відповідну клітинку листа-основи кольоровим боком до нього, а відповіддю догори. Якщо одночасно у декількох членів однієї команди знайшлася картка з правильною відповіддю ( що неможливо), то вони мають право на обговорення. Коли один з учасників обговорення впевнений у своїй правоті, то він кладе свою картку на потрібну клітинку таблиці, а решта учасників відмічають свої «засвічені» картки в експертів (- 1 бал). Якщо ж під час обговорення учні не прийшли до спільної думки, то вони всі за це отримують по одному штрафному балу. Коли таблиці кожної команди покрились відповідями експерти накривають таблиці третім листом і обережно перевертають все це на другий бік. Коли знімається верхня основа всі бачать чотири чудові кольорові картини. (при умові, що всі учасники розв’язали правильно всі завдання) Умови оцінювання: експерти і спостерігачі разом оцінюють результати гри. Якщо картина вийшла правильною , то команда виграє, і усі її члени отримують оцінку «11». Якщо ж є помилки, то картка яка псує зображення , вилучається. Картка пронумерована, отже відомий учасник гри , який припустився помилки. За це йому знижується оцінка на 2 бали, а команда не може претендувати на перемогу. Приклади завдань для другого тура :
- Для функції у=2х2-3х знайти у(1/2),у(-2)
- Для функції у=-3х+5 знайти х при якому у(х)=0, у(х)=-1
-
Область визначення функції у= -

-
Область визначення функції у=
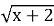
- Розв’язати рівняння 2х2-50=0
- Розв’язати рівняння 7х2=0
- Розв’язати рівняння 4х2+4=0
- Область значень функції у=х2-1
- Найбільше значення функції у= -3х2-1
- Функції f(х) і g(х) непарні. f(-2)=9, g(3)=-2.Обчислити -3 f(2)+2 g(-3)
-
Скоротити дріб
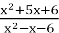
- Знайти координати точок перетину у=2х2+7х-4 та
у=2х-1
- Розв’язати графічно рівняння х3=2-х
-
Знайти область визначення функції у=
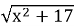
-
Знайти область визначення функції у=
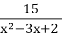
-
Знайти область визначення функції у=
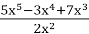
- Знайти найменше значення функції у= х2-9
- Зайти координати точок перетину функцій у=2х-х2 і
у= -2х
- Функції f(х) і g(х) парні. f(5)=2, g(-4)=-6.Обчислити -4 f(-5)+3 g(4)
- Знайти область значень функції у= (х+2)2+4
- Розв’язати рівняння 5х2+20х=0
-
Знайти область визначення функції у=
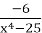
-
Знайти область визначення функції у=
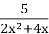
- Найменше значення функції у= х2-25
-
Знайти область визначення у=

Гра «Установи відповідність». На столах у роздавальному матеріалі зазначені назви функцій, їх графіки, формули, властивості, запишіть ланцюжок відповідностей.
Гра «Чи вмієте ви читати функції по графікам?». Накреслені графіки. Учні по графікам повинні визначити ту чи іншу властивість функції.
Добираючи ігри, продумуючи ігрову ситуацію, необхідно обов’язково поєднувати два елементи – пізнавальний та ігровий. Створюючи ігрову ситуацію відповідно до змісту програми, вчитель повинен чітко спланувати діяльність учнів, спрямовувати її на досягнення поставленої мети.
Дидактичні ігри допомагають вчителю виконати головну : не тільки дати учням певну базу знань, але й розвинути у них інтерес до навчання, навчити учитися.


про публікацію авторської розробки
Додати розробку
