Тема уроку: Паралельність площин. Розв’язування вправ.

Тема уроку: Паралельність площин.  Розв’язування вправ.

Мета уроку:

• освітня: закріпити вміння учнів застосовувати ознаки паралельності площин і властивості паралельних площин при розв’язуванні задач;
• розвивальна: організувати діяльність із розвитку уваги, математичного мовлення, робити висновки, узагальнювати факти, відпрацьовувати вміння говорити коротко, але по суті й переконливо;
• виховна: виховувати цілеспрямованість, вміння працювати в колективі, бути стійким перед труднощами, створювати ситуацію успіху для формування позитивного ставлення до себе «я можу у мене все вийде».

Тип уроку: удосконалення умінь і навичок.

Обладнання: мультимедійна дошка, проектор, слайди, конверт із завданнями.

• Очікувані результати: учні повинні вміти застосовувати ознаки паралельності площин і властивості паралельних площин при розв’язуванні задач.

Девіз уроку:

Не достатньо мати лише добрий розум.

Головне – це раціонально застосовувати його.

       Рене Декарт

ХІД УРОКУ

І. Організаційно-психологічна частина

Вітання з учнями. Почати сьогоднішній урок я вирішила зі слів            Е. Ільєнкова: «Досягнення успішного результату під час розв’язання задач – зовсім не привілей математики. Усе людське життя – це не що інше, як постійна постановка та бажання досягти успіху під час розв’язування все нових питань та проблем».

Як досягти успіху? Це питання постає перед нами практично щодня. І як доречно буде вам винести зі школи не тільки багаж теоретичних знань та практичних умінь, а й деякі рецепти досягнення успіху. Особливо є важливим це питання для нас зараз – бо ми вже почали роботу з підготовки до ДПА та ЗНО з математики.

1. Подивіться на екран.

Програма зовнішнього тестування з математики

Зміст навчального матеріалу	Знання	Предметні вміння та способи навчальної діяльності
Геометричні фігури. Аксіоми стереометрії. Взаємне розміщення прямих та площин у просторі. Побудови у просторі.	Аксіоми стереометрії, теореми та наслідки з них. Означення геометричних фігур у просторі та їх властивості. Взаємне розміщення прямих та площин у просторі.	Зображати геометричні фігури та їх елементи на площині. Використовувати правила паралельного проектування. Будувати перерізи многогранників і тіл обертання. Застосовувати означення, властивості та ознаки поданих у програмі геометричних фігур до розв’язування задач.

 

Слів не потрібно. Потрібно вміти застосовувати означення, властивості та ознаку паралельності площин  до розв’язування задач. Це є запорукою успішного складання зовнішнього тестування, шлях до вищих навчальних закладів, у стінах яких ви будемо навчатися для того, щоб стати кваліфікованими спеціалістами.

ІІ. Перевірка домашнього завдання

Одним із видів вашого домашнього завдання,  було створення   реклами теми «Паралельність площин», завдяки якій ви зможете переконатися у необхідності обраної теми для вашого подальшого життя.

 «Метод реклам»

 Реклама теми «Паралельність площин».

1. Увага!!! Якщо вас зацікавили ознаки паралельності площин та їх  властивості, то поспішайте підняти руку й хутчіш до дошки, щоб відчути впевненість у математичних знаннях. Вам гарантована висока оцінка.

Тож поспішайте!

2. Якщо вам набридло сидіти без діла, якщо ви хочете перевірити свої знання, - застосовуйте ознаку паралельності площин  та їх властивості при розв’язуванні задач. І ви дізнаєтеся, на що здатен ваш мозок!

ІІІ. Актуалізація опорних знань

1. Технологія «Асоціативний кущ».  Для розуміння наступного потрібно розуміння попереднього. Повторимо відомості про паралельні площини, це розширить ваші можливості у розв’язуванні задач.

             

        

Підготуємо наші зошити до роботи. Хочу нагадати, що під час роботи з діловими документами запорукою успіху є старанне, охайне. Уважне ставлення до цієї роботи. (Запис дати, теми.)

Графічний диктант

Якщо твердження правильне, учні ставлять знак , якщо неправильне — знак.

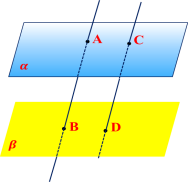
1. Якщо α ‖ β, то будь-яка пряма, паралельна площині α , буде паралельною і площині β.

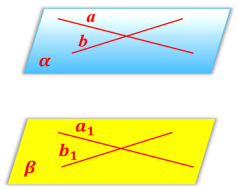
2. Якщо α ‖ β, то для будь-якої прямої a площини α існує паралельна їй пряма b площини β.

3. Якщо дві прямі, одна з яких лежить у площині α, а друга — у площині β, не мають спільних точок, то α ‖ β.

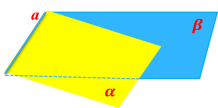
4. Якщо дві прямі площини α паралельні відповідно двом прямим площини β, то α ‖ β.

5. Якщо кожна пряма площини α паралельна площині β, то α ‖ β.

6. Якщо α ‖ β, то будь-яка пряма, що перетинає площину α, перетинає і площину β.

7. Якщо α ‖ β, то будь-яка пряма площини α паралельна площині β.

8. Якщо деяка пряма площини α паралельна площині β, то α ‖ β.

9. Якщо кожна пара прямих, одна з яких лежить у площині α, а друга — у площині β, не мають спільних точок, то α ‖ β.

10. Якщо α ‖ β, то для будь-якої прямої a площини α існує пряма b у площині β така, що a і b мимобіжні.

11. Якщо α ‖ β, то будь-яка пряма площини α є мимобіжною з будь-якою прямою площини β.

12. Якщо α ‖ β, то будь-яка пряма площини α паралельна кожній прямій площини β.

Ключ до диктанту дає можливість учням оцінити себе. Відповіді обговорюються, у разі потреби супроводжуються ілюстраціями.

Ключ-відповідь до графічного диктанту

---------- ----- ----- ----- -----

1     2    3     4   5  6  7    8   9 10  11   12

IV. Застосування знань учнів до розв’язування вправ

1. Робота біля дошки. Розв’язування задач з коментарем.

 Подивіться на екран. Перед вами три різнорівневі  задачі. Виберіть завдання свого рівня  та запрошую до дошки.

№ 297 (в) - середній рівень;

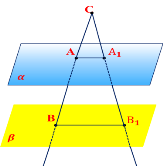Через точку С, яка лежить поза паралельними площинами α і β, проведено прямі а і b, що перетинають площину α в точках А і А₁, а площину β у точках В і В₁ відповідно. Знайдіть АА₁, якщо АС = 2 см, ВВ₁ = 8 см, СВ = АА₁.

1. № 301 – достатній рівень;

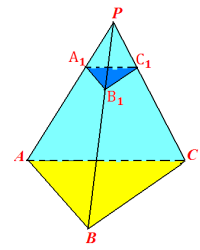
Точка А₁ ділить ребро РА тетраедра РАВС у відношенні РА₁ : А₁А = 2 : 3. Побудуйте переріз тетраедра площиною, яка проходить через точку А₁ паралельно площині (AВC). Обчисліть периметр і площину перерізу, якщо – рівносторонній трикутник і    AВ = 20 см.

 

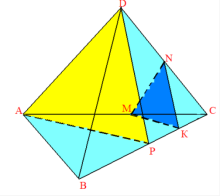Оскільки січна площина паралельна площині ANC, то вона паралельна прямим AN, NC і CA. Отже, січна площина перетинає бічні грані тетраедра по прямих, паралельних сторонам трикутника ANC. Проведемо через точку M пряму, паралельну AN, і позначимо буквами M і K точки перетину цієї прямої з ребрами DB і DA відповідно. Потім через точку K проведемо пряму, паралельну AC, позначимо буквою L точку перетину цієї прямої з ребром DC. Отже, трикутник KML — шуканий переріз.

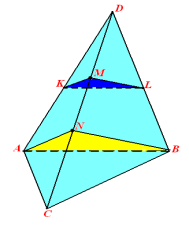
2. № 311 - високий рівень.

Дано тетраедр АВСD. Побудуйте переріз тетраедра площиною, яка проходить через точку M паралельно площині (ADP). Знайдіть сторони  перерізу, якщо AВ =  АC = 20 см, ВС = 16 см,  AD = DВ = DС = 17 см.

Оскільки січна площина паралельна площині BDC, то вона паралельна прямим DB, BC і DC. Отже, січна площина перетинає бічні грані тетраедра по прямих, паралельних сторонам трикутника BDC. Проведемо через точку M пряму, паралельну DB, і позначимо буквами M і N точки перетину цієї прямої з ребрами DA і AB відповідно. Потім через точку N проведемо пряму, паралельну BC, позначимо буквою K точку перетину цієї прямої з ребром AC. Отже, трикутник MNK — шуканий переріз.

 

 Технологія «Мозковий штурм».

Після презентації умови задачі, яку необхідно розв’язати, учитель пропонує всім висловити ідеї, коментарі, шляхи розв’язання. Усі пропозиції записуються на дошці в порядку їх оголошення без зауважень, коментарів чи запитань. Необхідно заохочувати всіх до висування якомога більшої кількості ідей. На слайді запис:

• Вкажіть усе, що спаде на думку.
• Не обговорюйте і не критикуйте висловлення інших.
• Розширення запропонованої ідеї заохочується.
• На закінчення обговорюються й оцінюються запропоновані ідеї.

Розв’яжіть задачу

Дано три паралельні площини: Нехай – точки перетину даних площин з довільною прямою. Довести, що відношення довжин відрізків : не залежить від прямої, тобто однакове для будь-яких двох прямих.

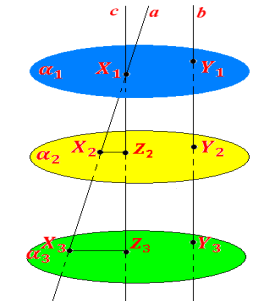Розв’язання

Нехай пряма a перетинає площини у точках відповідно. Нехай друга пряма b перетинає площини у точках Y₁, Y₂, Y₃ відповідно.

Доведемо, що.

Проведемо через точку пряму c, паралельну прямій b. Нехай c перетинає у точках і  відповідно. Площина, у якій лежать прямі a і c, що перетинаються, перетинає паралельні площини   по паралельних прямих і . Отже,, звідки випливає, що, однак за властивістю паралельних площин        , а  . Отже,  що. Таким чином, відношення не залежить від обраної прямої, що й треба було довести.

Примітка. Факт, доведений у задачі, називають теоремою Фалеса в просторі.

.

 

 

V. Систематизація знань, умінь під час виконання самостійної роботи

 Щоб сьогодні на уроці кожний міг з упевненістю сказати, що він досяг успіху, необхідно попрацювати над виконанням аналогічних завдань ще й самостійно. Давня китайська мудрість говорить: «… Покажи мені – і я запам’ятаю, дай мені діяти самому – і я навчусь…»

 Уміння працювати самостійно є дуже важливим і в навчанні, і в житті, тому на цьому етапі ми не тільки будемо систематизувати наші навчальні досягнення, а й продовжувати розвивати вміння працювати самостійно. Крім того, для досягнення успіху в житті важливим є наявність друзів, партнерів. Тому цю самостійну роботу ми проведемо у формі взаємодопомоги – у вас є вибір працювати повністю самостійно або скористатися допомогою. Перед вами картка із завданням різнорівневої самостійної роботи.

Самостійна робота

Середній рівень

№ 298 (в)

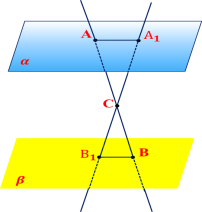
 Точка С лежить між паралельними площинами α і β. Через точку С проведено прямі а і b, які перетинають площину α в точках А і А₁, а площину β у точках В і В₁ відповідно.        Знайдіть АА₁, якщо АС = 1 см, ВВ₁ = 6 см, АВ = АА₁.       

Достатній рівень

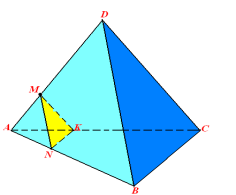
№ 300

Дано тетраедр АВСD. Побудуйте переріз тетраедра площиною, яка проходить через точку M паралельно площині (ANC). Обчисліть периметр і площину перерізу, якщо AN =  NC = 25 см,  AC = 14 см.

Розв’язання

Оскільки січна площина паралельна площині ANC,                                                                                                                                                                                                                                       то вона паралельна прямим AN, NC і CA. Отже, січна площина перетинає бічні грані тетраедра по прямих, паралельних сторонам трикутника ANC. Проведемо через точку M пряму, паралельну AN, і позначимо буквами M і K точки перетину цієї прямої з ребрами DB і DA відповідно. Потім через точку K проведемо пряму, паралельну AC, позначимо буквою L точку перетину цієї прямої з ребром DC. Отже, трикутник KML — шуканий переріз.

Високий рівень

1. № 310                                                                                                                                                                                                                                                                                                                                                                       

Дано тетраедр АВСD. Побудуйте переріз тетраедра площиною, яка проходить через точку M паралельно площині (ВC). Знайдіть периметр і площу перерізу, якщо – рівносторонній і його площа дорівнює 64 см².

 

 

 

 

 

Подивіться на екран, перевірте результати самостійної роботи. Підніміть руку ті, хто самостійно чи скориставшись допомогою дістав правильну відповідь. Молодці ви досягли успіху. Іншим раджу не засмучуватись – ви теж досягли певного успіху.

Український філософ і письменник Г. С. Сковорода писав: «Найкраща помилка та, яку допускають під час навчання».

VI  Домашнє завдання.

Працюючи разом, маючи поряд надійних партнерів ми досягли успіху. Але в житті і в навчанні часто для досягнення успіху треба вміти працювати без допомоги, повністю самостійно. Тому продовжувати працювати над розв’язанням задач з теми «Паралельність площин»  ви будете вдома, під час виконання домашнього завдання, яке ви оберете за своїм рівнем.             

Середній рівень:

Дві паралельні площини α і β перетинають сторону AB кута ABC у точках D і D₁, а сторону BC — відповідно в точках E і E₁. Знайдіть довжину відрізка DE, якщо BD = 12 см, BD₁ = 18 см, D₁ E₁ = 54 см.

Достатній рівень:

Точка K не лежить між паралельними площинами α і β. Через точку K проведено прямі a і b, які перетинають площину α у точках A₁ і A₂, а площину β — у точках B₁ і B₂ відповідно. Знайдіть KB₂ і KA₁, якщо A₁A₂:B₁B₂ = 3:4,     A₁ B₁= 7 см, KA₂ = 12 см.

Високий рівень:

Три прямі, які проходять через точку S, перетинають площину α у точках A, B, C, а паралельну площину β — у точках A₁, B₁, C₁ відповідно. Точка S лежить між площинами α і β,  SB:BB₁ = 2: 3. Знайдіть площу трикутника       A₁ B₁ C₁, якщо площа трикутника ABC дорівнює 16 см².

 

VII. Самооцінка учнів.

На початку уроку учні отримали картки самоконтролю, учитель пропонує учням заповнити їх. Оцінивши свою роботу на уроці і виставити собі від 0 до 3 балів за кожний із критеріїв.

• Я допомагав(ла) іншим учням, заохочував(ла) їх до роботи.
• Я вносив(ла) вдалі пропозиції, які були враховані в ході розв’язування.
• Я активно працював(ла) у групі.
• Я узагальнював(ла) думки інших та просував(ла) роботу класу вперед.

VIII. Підсумок уроку:

 Рефлексія ( усвідомлення результатів уроку – технологія «Мікрофон» )

1. Чи досягли ви очікуваних результатів особисто, клас у цілому ?
2. Що сподобалось особливо під час уроку ?
3. Над якими навичками, вміннями ще треба працювати?
4. Кому ти хочеш подякувати за роботу?

Вчіть свій розум та душу бачити хороше – і тоді дорога до успіху буде для вас відкрита.

 Дякую вам за підготовку та проведення цього уроку, за роботу на ньому. Бажаю всім присутнім успіху!