Урок. Конспект уроку з геометрії для 10 класу "Теорема про три перпендикуляра"

Урок з геометрії 10 клас

 

Тема уроку:  Теорема про три перпендикуляри

 

Мета:

•                   навчальна: актуалізація опорних знань з теми: «Перпендикуляр та похила»;  формування знань з теми: "Теорема про три перпендикуляри"; навчання учнів використанню отриманих знань при розв`язуванні задач.

•                   виховна: формування поваги до культури та історії свого народу; формування творчої, працелюбної особистості; розвиток духовної культури особистості; розвиток індивідуальних здібностей і забезпечення умов їх реалізації.

•                   розвиваюча: формування загально-навчальних вмінь та навичок (робота з підручниками, узагальнення, планування, самоконтроль тощо); сприяння розвитку волі, наполегливості під час навчання, розвитку пам’яті (уяви, технічного розвиток зацікавленості учнів).

Тип уроку:  урок засвоєння нових знань.

Обладнання та наочність: модель трьох перпендикулярів (зроблена з картона і трьох олівців), підручник.

 

Хід уроку

 

I. Організаційний етап

Вчитель вітається з учнями і оголошує мету, план уроку та завдання уроку. 

Вчитель: Сьогодні на уроці ми розглянемо теорему про три перпендикуляри,  навчимося її застосовувати при розв’язуванні різних задач, Ви зможете переконатися у необхідності її використання у повсякденному житті.

II. Актуалізація опорних знань

Вчитель: Перед початком роботи згадаємо матеріал попереднього уроку.

Вчитель проводить фронтальне опитування у вигляді бесіди.

 

Колективна робота учнів

1) Що таке перпендикуляр, проведений з даної точки до даної площини?

Основа перпендикуляра?

2) Що таке похила, проведена з даної точки до площини?

Що таке проекція похилої?

3)  Сформулюйте властивості перпендикуляра і похилої.

4) Скільки перпендикулярів можна опустити з даної точки до даної площини?

5) Скільки похилих можна побудувати з даної точки до даної площини?

                                                        А

 

 

 

 

 

 

(на дошці малюнок підказка)

 

Вчитель: Давайте об’єднаємося у групи за рядами, розв’яжемо задачу і запишемо відповідь на дошці.

 

Групова робота учнів

Задача 1(усно)

Назвіть на малюнку:  1. перпендикуляр; 2. основу перпендикуляра; 3. похилу; 4. проекцію похилої.

 

Робота в парах

Вчитель: Запропонуйте аналогічну задачу сусіду, обговоріть.

 

Мотивація  учіння

Значний внесок у розвиток геометрії зробили такі українські математики як Іван Федорович Тесленко (1908-1994) та Борис Якович Букрєєв (1859-1962).

Іван Федорович Тесленко створив підручник з геометрії, у якому дохідливо розкрив методи геометрії, розкрив особливості розв’язування планіметричних та стереометричних задач.

Борис Якович Букрєєв  працював в Києвському університеті і виховав не одне покоління науковців і вніс значний внесок у розвиток геометрії..

ІІІ. Пояснення нового матеріалу та способів виконання дій

Вчитель показує модель до теореми про три перпендикуляри і запитує: Чому дорівнює кут АСК та кут ВСК?

 ^К  мал.1

Відповідь учнів: Дані кути дорівнюють . (можна виміряти кути транспортиром)

Вчитель: Запишіть наступну теорему

Теорема( про три перпендикуляра)

Якщо пряма, проведена на площині через основу похилої, перпендикулярна до її проекції, то вона перпендикулярна і до похилої.

Вчитель: Зробіть  малюнок 1 у зошиті. Питання до класу:

Як на вашу думку, чому теорема називається теоремою про три перпендикуляра?

Відповідь учнів:(записуємо)

Вчитель: Спробуйте у теоремі змінити місцями умову та наслідок і запишіть теорему обернену до даної.

 

Індивідуальна робота учнів

Діти самостійно формулюють теорему, і своє трактування записують у зошити. По черзі учні зачитують свої варіанти.

Теорема( обернена)

Якщо пряма, проведена на площині через основу похилої, перпендикулярна до похилої , то вона перпендикулярна і до її проекції.

 

Вчитель: У мене є площина і пряма, що перетинає цю площину. Підкажіть, як знайти кут між прямою та площиною?

Учні висловлюють свої думки, показують відповідь на моделі. Після обговорення приходимо до правильного розуміння і записуємо означення.

Означення. Кутом між прямою і площиною називається кут між цією прямою і її проекцією на площину.

a-похила; b-проекція похилої а;

 

ІІІ. Розв`язування задач

Первинне закріплення

 

Колективна робота учнів

Вчитель: Пропоную розв'язати таку задачу усно

 

Задача 1(408)

 

Актуалізація знань

Вчитель: Як Ви вважаєте, які знання нам потрібні  при  розв`язуванні задач з цієї теми?

Учні:

1. Теорему Піфагора.

2. Співвідношення у прямокутному трикутнику.

 

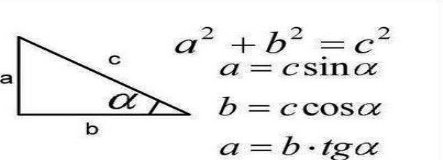
Доповнює вчитель і діти записують:

3.Якщо деяка  точка однаково віддалена від усіх сторін многокутника, то основа перпендикуляра, проведеного з цієї точки до площини многокутника, також однакова віддалена від сторін многокутника, тобто  є центром вписаного у многокутник кола.

 

Прикладне значення цієї теми

У реальному житті ми часто зустрічаємо точки простору, рівновіддалені від усіх сторін многокутника: шпиль вежі, вершина даху, вісь болта, вал шестерні, вершина опори ЛЕП. Отже, є потреба вивчити властивості всіх таких точок.

 

Колективна робота учнів

Задача 2

 

Відстань від точки М до сторін ромба АВСD дорівнює 15см, а до площини АВС – 9 см. Знайдіть радіус кола, вписаного в ромб.

Вчитель: Яке коло називається вписаним? Яку властивість дотичної Ви знаєте?

Дано: АВСД-ромб; МО=9 см МК=15 см Знайти ОК? Розв’язання: ОК-радіус вписаного кола; За т. Піфагора: ОК2=МК2-МО2 ОК2=152-92=(15-9)(15+9)=6*24=144 ОК=12 см Відповідь:12 см

Вчитель:  Пропоную учням за кожною партою записати відповіді до задачі 3, а тоді один у одного перевірити.

 

Робота учнів у парах

Задача 3

1.Кут(ДС1;АВСД)= Кут(ДС1;ДС). 2. Кут(В1Д;АВСД)= Кут(В1Д;ВД). 3. Кут(В1Д;ДД1С1С)=Кут(В1Д;ДС1).

 

Колективна робота учнів

Задача 4 (417.1)

З вершини В прямокутника АВСД проведено перпендикуляр ВМ до його площини. АВ=5 см, Вс=16 см, ВМ=12 см. Знайти відстані від точки М до СД і АД? (у підручнику є готовий малюнок, але краще дати задачу без готового малюнка)

Дано: АВСД-прямокутник; ВМ-перпендикуляр; АВ=5 см; ВС=16 см; ВМ=12 см. Знайти відстані від точки М до СД і АД? Розв’язання: АМ і СМ- шукані відстані(за т. про три перпендикуляра);   АВМ та СВМ-прямокутні (за озн. перпендикуляра): За теоремою Піфагора: АМ2=ВМ2+АВ2 АМ2=122+52 АМ=13 см СМ2=ВМ2+ВС2 СМ2=122+162 СМ=20 см Відповідь: АМ=13 см; СМ=20 см

 

Вчитель: Хто зробив задачу може спробувати самостійно розв'язати наступну задачу.

Вчитель вішає на дошку зображення будинку та пропонує тим хто бажає, зробити малюнок до задачі.

 

Індивідуальна робота учнів  при розв'язуванні задач прикладного змісту

 

Задача 5 

 

1.               Чотирисхилий дах будинку квадратної форми зі стороною 16м має висоту 6м. Скільки квадратних метрів дахового заліза піде на покриття, якщо витрати на згин і обрізки становлять 6%?

                                 

                          

 

Розв’язання:

                                                                    Нехай дано  квадрат АВСD ,

АВ = 16м. EO ┴ (ABCD) , EO=6м.

Оскільки т.Е рівновіддалена від сторін АВСD, то т.О – центр вписаного кола ( точка перетину діагоналей). Якщо ЕК ┴ СD, то за

оберненою теоремою про три перпендикуляри ОК ┴ СD, ОК=8 м.

З ∆ EOК, <O=90⁰, за теоремою Піфагора EK²= EO² + ОК².

.    S= 4S_∆CDE,         

       S_∆CDE=CD·ЕK=

·16·10=80(м²).

Оскільки таких трикутників чотири, то

S= 4·80= 320(м²).

S₁=320+0,06·320=339,2 (м²).

Відповідь: 339,2 м².

 

ІV. Формування нового навчального досвіду

Вчитель пропонує завдання на індивідуальних картках

Самостійна робота

1  варіант

Задача 1

 

Згідно даного малюнка запишіть усі похилі, перпендикуляри, проекції похилих та основи перпендикулярів.

Вкажіть для яких трьох перпендикулярів, зображених на малюнку, можна записати теорему про три перпендикуляри.

 

                                                        А

 

 

 

 

 

Задача 2

 

Дано куб АВСДА₁В₁С₁Д₁. Вказати кут між прямою А₁С та площиною ДСС₁.

 

І1  варіант

Задача 1

 

Згідно даного малюнка запишіть усі похилі, перпендикуляри, проекції похилих та основи перпендикулярів.

Вкажіть для яких трьох перпендикулярів, зображених на малюнку, можна записати теорему про три перпендикуляри.

                                                        В

 

 

 

 

 

 

Задача 2

 

Дано куб АВСДА₁В₁С₁Д₁. Вказати кут між прямою А₁С та площиною АВС.

V. Підведення підсумків. Повідомлення домашнього завдання.

Д/З  параграф 11-вивчити, 9 та 10-повторити

№409, 417(2)

Додаткове завд.: №418

 

 

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

 

1. Бурда  М.І. Геометрія:  підручник для 10 клас ,-К.:Зодіак, 2016.-176 с. 
2. Капіносов А.М. та інші. Математика: посібник для підготовки до зовнішнього незалежного оцінювання.- Тернопіль: Підручники і посібники, 2010.-400 с.