Творчий звіт з теми: «Активізація пізнавальної діяльності учнів на уроках математики у 5 - 6 класах»

 

 

 

 

 

Творчий звіт з теми:

«Активізація пізнавальної діяльності учнів на уроках математики

у 5 - 6 класах»

2018 – 2019р.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

При вивченні математики в класах дуже важливо не тільки дати дітям міцні знання, а й не відштовхнути школярів холодною сухістю і суворістю цариці наук, захопити їх цим предметом.

Зацікавити учнів математикою, показати їм могутність і красу, допомогти зрозуміти її — завдання кожного учителя математики. Здатність бачити цікаве і дивуватися приносять дітям радість, породжують творчі поривання, розвивають уяву, що дуже важливо на уроках математики. Працю вчителя в цьому напрямку значно полегшує поєднання прямого подвійного зворотного зв'язку з пізнавально - ігровими ситуаціями, тому що гра і дитина - невіддільні. По проблемам активізації пізнавальної діяльності свого часу було надруковано багато матеріалу. В цій роботі я пропоную декілька прикладів , методів та прийомів розвитку пізнавальної активності учнів, які використовуються мною на уроках математики в залежності від віку дітей, матеріалу, теми та особливостей класу.

Усі запропоновані прийоми народжуються поступово, протягом багатьох років роботи: частина з них запозичена з досвіду роботи інших вчителів, частина — із книг, методичних розробок, частина — мої розробки. Але всі вони пройшли перевірку часом, подобаються дітям і мені, як вчителю.

Однією із основних і першорядних задач при вивченні математики є      відпрацювання учнями навичок гарних усних обчислень. Але одноманітність завдань у вигляді прикладів на обчислення знижує зацікавленість як до рахунку так і до уроків взагалі. Тому вчителю необхідно мати про запас арсенал різних прийомів, направлених на відпрацювання обчислювальних навичок учнів і, в той же час, не зловживати працьовитістю дітей. З метою підготовки учнів до уроків можна пропонувати приклади, які оформлені у вигляді блок-схем; будувати алгоритми; великі приклади на багато дій розв'язувати за допомогою естафети.

Відпрацювання обчислювальних навичок сприяє гра “Рибалки” : з чотирьох — п'яти запропонованих на рибках прикладах діти 1-го варіанту «відловлюють» приклади з відповіддю, наприклад 5, а учні 2- го варіанту приклади з відповіддю 6.

Наступний вид завдань - приклади по колу, які допомагають дітям здійснювати самоконтроль, а вчителю полегшує перевірку робіт. Подобається учням, коли вчитель дає завдання на виправлення заздалегідь зроблених помилок у розв'язуванні, на відновлення частково стертих записів. Недописана фраза, недорозв’язувана  задача, недоказана умова в задачі стимулюють роботу учнів. Полюбляють діти всіх вікових категорій , коли уроки пожвавлені задачами - жартами, завданнями на увагу.

Найрізноманітніші форми кодування відповідей привертають увагу дітей не менш ніж цікава задача. Наприклад, ось такі чотири види таких завдань:

1.               Запрограмоване опитування.
2.               На дошці поряд з прикладом вчитель пропонує відповідь, закодовану літерами, учні розв’язують приклад, обирають правильну відповідь і записують у зошит літер v-код, яка співпадає з правильною відповіддю. Бажано, щоб в кінці обчислювання в учнів з’явилося слово. Можна закодувати літерами правильні відповіді до вправ домашнього завдання так, щоб отримане слово або словосполучення були темою уроку.
3.               Відповіді закрити картками. Діти дають відповідь, відкривають її, перегорнувши картку, закріплюють її поруч з відповіддю. На зворотному боці картки літери, які утворюють якесь слово, вислів (бажано похвалу).

Цілком зрозуміло, що це не повний перелік, при бажанні їх можна і урізноманітнити, і доповнити.

Під час усних обчислень з усім класом зручно використовувати різні ігри, проводити змагання між рядами.

Зокрема, за принципом приклади по колу будуються ігри “ Математичне доміно ”,  “Математичні бар’єри” .

На уроках математики зручно використовувати математичне лото двох видів: карточка з відповіддю накладається на карточку з прикладом; приклади подаються на дошці, а учні жетоном накривають карточку з відповіддю.  Другий вид лото зручніший , тому що одну карточку з числами — відповідями можна використовувати неодноразово.

Великий вибір ігор пропонує нам телебачення немає нічого складного для того, щоб провести  “Щасливий випадок ”, “Хто найрозумніший” і “Зоряний час”, але з математичним змістом запитань і завдань.

Форма вибору завдань учнями може бути також різноманітною: наприклад, кидком кубика, на граннях якого вказані номера завдань або обираючи одну з геометричних фігур, під якою вказані номери вправ, що дозволяє вчителю виявити психологічні особливості дитини (доброзичливі, як правило, обирають коло) або витяганням номерів, закодованих літерами (в кінці уроку з цих літер можна запропонувати скласти слово).

Назву ще ряд прийомів та методів за допомогою яких можна активізувати пізнавальну діяльність учнів.

1.      Груповий метод при розв’язуванні задач. Робота в парах.

2. Викладання матеріалу блоком. При цьому учні отримують так званий “математичний блок”, в якому зібрані

•         запитання для взаємного опитування ;
•         опорний конспект по даній темі;
•         обов’язкові наслідки;
•         залікове завдання; з цим “блоком” завдань учні працюють протягом вивчення всієї теми.

 3. Використання проблемних ситуацій.

 4. Різні форми роботи з підручниками.

  5. Використання різноманітних видів заохочень (жетони, слова, вручення посвідчень “кращому математику ”, диференціювання домашнього завдання).

 6. Використання на уроках елементів історизму, зацікавлення    (уроки - казки, уроки - мандрівки, уроки - кросворди).

 7. Спостереження за відповіддю, рецензування за схемою - планом.

Велике значення має організаційний момент кожного уроку. Як швидко налаштувати  дітей на роботу, але зробити це без понукань і суворості ? Я часто проводжу організаційний момент у вигляді “математичної зарядки”.

Заздалегідь готую декілька карточок із простими прикладами. Приклади даються із відповідями. На одних карточках відповіді правильні, а на інших - не -правильні. Кожна вправа зарядки складається з двох рухів. Вчитель по черзі показує класу карточки, а учні у відповідь виконують визначений рух.

Наприклад, якщо відповідь вірна - руки вгору, неправильна - руки вперед. Спочатку діти не можуть зосередитись, не попадають в ритм. Але поступово зосереджуються , а темп зарядки прискорюється, як підсумок, через 2-3 хвилини ми отримуємо клас, повністю підготовлений до роботи.

Зарядка може складатися з 2-3 вправ і проводитись по самим  різним методам .

Складання комплексів вправ корисно доручати дітям. Вони це виконують з великим задоволенням.

Наведу приклад математичної зарядки «Дільники і кратні» 

Перша  вправа: Правильна  відповідь – руки вперед  , неправильна – руки вгору.

  

2*0,3=0,6;	0,5*10=50;	7*12=84
6:100=0,6;	6:2=3	7+0,5=0,75.

 

Друга вправа: Всі стоять, руки на поясі, правильна відповідь - поворот праворуч, неправильна - поворот ліворуч

 2 — дільник числа 222;  1 - має один дільник;

15 — кратне 10;

Дуже допомагають активізувати учнів па протязі уроку так званий швидкий диктант. Від звичайних математичних диктантів їх відрізняють три особливості:

•   завдання не однакові за складністю. Спочатку пропонуються дуже легкі, а потім складніші і складніші.

Темп диктування змінюється від повільного до швидкого;

•                   Одночасно на закритій дошці працює один учень, що дає можливість зразу ж перевірити відповіді.

В курсі математики, на мій погляд, щонайбільше серйозних правил та означень. Як домогтися від дітей зацікавленого, захопленого вивчення цих правил? Для цього я використовую загальні опитування і гру в математичні карти.

Щодо загальних опитувань то я проводжу їх з самого початку вивчення теми. При опитуванні учнів вони самі вибирають серед відповідаючих найкращих знавців правил та означень. Перед заліковими уроками вони навіть “ екзамен ” складають на звання  “консультанта ”.  Ті , хто його отримує , стають моїми найпершими помічниками під час проведення залікових уроків. Кожен з них тепер опитує групу учнів з 3 - 4 чоловік, а мені здає “ маршрутний лист” Використання потреби дітей у грі породжує особливий вид ігор — дидактичні ігри і особливу форму занять - ігрову.  Під дидактичною грою підрозумівається гра, яка використовується з метою навчання і виховання.  Гра — продумана діяльність, мотивація якої лежить у самій діяльності. Вона не пов’язана з необхідністю, участь в ній визначається бажанням. Дидактична гра відрізняється тим, що участь у ній обов’язкова і визначається вимогою вихователя. Дидактичні ігри та ігрові заняття повинні бути різноманітними і розроблятися з урахуванням особливостей предмета. Вся різноманітність ігри повинна складати продуману систему. Це може послужити додатковим джерелом систематичних і міцних знань. Система ігор повинна включати види:

А) навчаючі і контролюючи (за призначенням);

Б) групові (колективні) і індивідуальні;

В) рухливі і тихі (за реакцією);

Г) “швидкісні” та “якісні” (за темпом)

Д) тематичні та універсальні;

Е) настільні, настінні та інші (за місцем проведення).

Така класифікація, проведена за різними підставами, не є остаточною та суворою, оскільки кожну з дидактичних ігор можна віднести до кількох видів. Наприклад, гра може бути і колективною, і навчаючою, і тихою тощо.

За призначенням будемо відрізняти ігри навчаючs і контролюючі. Гра називається навчаючою, якщо учні, приймаючи в ній участь, набувають нових навичок, знань, або змушені їх придбати перед грою. В другому випадку гра використовується як мотив, стимул для отримання нових знань. Гра називається контролюючою, якщо для участі в ній дітям достатньо мати відомі їм знання. Її метою є закріплення раніш отриманих знань, контроль їх.

На практиці частіше за все ігри бувають одночасно і навчаючі і контролюючі.

Лише в залежності від співвідношення між метою можна говорити про навчаючий або контролюючий характер тієї чи іншої гри.

Умовно можна виділити і виховуючи ігри, які мають за мету виховання окремих рис особливості (уваги, спостережливості, кмітливості тощо) і ніяких конкретних математичних занять не вимагає. Наприклад гра “Веселий рахунок” (на увагу, швидкість орієнтацію).

Відомо, що учням середніх класів притаманне відчуття колективізму, відчутно бажання приймати участь у житті колективу, як повноправний його член, прагнення спілкуватися з товаришами, приймати участь у спільній з ними діяльності. Тому їхні ігри частіше за все приймають колективні форми. Але їх цікавлять і індивідуальні ігри, але, як правило, пов’язані з розумовими зусиллями, тобто інтелектуальні ігри , в яких вони можуть перевірити свої розумові здібності. Більшість з них можна віднести до тих ігор, або, як їх називають, настільних. Це “математичне лото”, «математичні головоломки із сірниками». Деякі з них сприяють закріпленню навичок та умінь. Виходячи із особливості предмету математики, потрібно розрізняти два види ігор — змагань: по - перше, це ігри, перемога в яких забезпечується швидкістю дій без втрати якості розв’язувань (швидкістю виконання обчислень, перетворень, швидкістю розв’язування задач, доведення теорем тощо), умовно назвемо їх іграми на швидкість; по - друге, це ігри, перемога в яких забезпечується і швидкістю дій, але головним чином, правильністю розв'язувань, безпомилковим їх виконанням. Не стільки швидко, скільки точно.  Їх можна назвати іграми на якість.

Перші корисні тоді, коли потрібен автоматизм дій, другі — напрямлені на серйозні обчислення і застосовуються тоді, коли необхідна вдумлива робота над громіздкими обчисленнями, важкими задачами, теоремами тощо. Вони необхідні для виховання серйозного відношення до обчислень, по можливості є відокремленими від поспішливості, квапливості, які можуть перешкодити зосередженій роботі.

Найбільш важливими є ігри на якість, оскілки вони допомагають розв'язати одну задачу — активізувати розумову діяльність учнів, примусити їх активно розмірковувати над задачею, розвивати наполегливість, настирливість.

Слід розрізняти ігри одиночні і універсальні. До одиночних ігор віднесемо ті, правила яких не дають можливості міняти зміст ігри; вони розроблені з урахуванням особливостей конкретного матеріалу, їх ще називають тематичними. До універсальних ігор віднесемо ігри, які можуть бути розроблені по широкому колу питань шкільної програми, по будь-якій темі, розділу.

Для того , щоб навчання було ефективніше, необхідно всю різноманітність прийомів навчання, в тому числі і дидактичні ігри, використовувати в комплексі. Граючи, діти не помічають, що набувають тих або інших математичних навичок..

Дидактичні ігри на уроках математики можна використовувати для знайомства дітей з новим матеріалом і для його закріплення, для повторення раніш набутих понять для їх повного і глибокого усвідомлення, формування обчислювальних, графічних вмінь та навичок, розвитку основних прийомів мислення, розширення світогляду.

Систематичне використання ігор підвищує ефективність навчання. Дидактичні ігри підбираються у відповідності з програмою. Підбираючи ігри, продумуючи ігрову ситуацію, необхідно обов’язково поєднувати два елементи — пізнавальний і ігровий.

Створюючи ігрову ситуацію, вчитель повинен чітко спланувати діяльність учнів, направити їх на досягнення поставленої мети. Коли визначено завдання, вчитель надає йому ігровий задум, продумує ігрові дії. Через ігровий задум виникає зацікавленість до ігри. А коли з’являється особлива зацікавленість, виникає і активність, і творчі думки, і дії , і переживання за себе, команду або весь колектив — все, без чого не можлива ігрова діяльність.

Готуючись до уроку, вчитель повинен заздалегідь підготувати необхідний дидактичний матеріал, обміркувати послідовність ігрових дій, організацію учнів, обсяг ігор за часом, контроль, підведення підсумків і виставлення оцінок.

Проводити ігри ,створювати ігрову ситуацію важливо на кожному уроці.

Гру можна запропонувати на початку уроку (усний рахунок, повторення матерілу, який буде опорою всього уроку. Ігри ,які проводяться на початку уроку ,повинні “ розбудити ” думки учнів, допомогти їм зосередитися і виділити основне, головне, направити увагу на самостійну діяльність.

Наприклад ,перед вивченням поняття , “ дріб ”  учням було запропоновано дома вирізати по п’ять синіх, червоних, білих кругів.

На уроці вони отримали завдання розділити три круга порівну між чотирьох товаришів. Потім було завдання: віддати своєму сусіду 1/4, 2/4 частини круга. Так “граючи” долями круга, учні знайомились із додаванням та відніманням дробів, у яких однакові знаменники. Задача “ Поділити порівну 15 кругів між 4 учнями ” привела їх до поняття мішаного числа, правильного і неправильного дробу.

Іноді гра може бути фоном для побудови всього уроку. Коли учні вломленні, їм можна запропонувати рухливу гру.

Щоб ігрова діяльність на уроці проходила ефективніше і давала бажані результати, нею треба керувати, забезпечуючи виконання наступних вимог:

1.               підготовленість учнів до участі в грі. Кожен учень повинен засвоїти правила  гри, чітко усвідомити її мету, кінцевий результат, послідовність дій, мати необхідний запас знань;
2.               забезпечення кожного учня необхідним дидактичним матеріалом;
3.               чітке, зрозуміле пояснення завдань гри;
4.               складну гру слід проводити поетапно, доки учні не засвоять окремих дій, а далі можна запропонувати всю гру;
5.               дії учнів треба контролювати, своєчасно виправляти, направляти і оцінювати;

6) ні в якому разі не можна припускати приниження гідності (принижуючі порівняння, оцінка за поразку в грі, насміхання.)

Постільки гра повинна проводитись систематично, вчитель повинен обмірковувати все до найменших подробиць, а саме:

1) необхідно створити умови для проведення постійних ігор - змагань між учнями, які сидять на різних рядах, та для індивідуальних ігор;

2)  підібрати мінімальну кількість ігрового  матеріалу для проведення ігор;

3) обміркувати місце зберігання ігрового матеріалу;

4) ігровий матеріал повинен бути чітко систематизований і згрупований так, щоб ним було зручно користуватися;

5) слід звернути увагу на те, як розміщені діти. Учнів треба розсадити так, щоб за кожною партою сидів один учень сильніший по знанням, а другий слабший. У такому випадку ігри між сусідами по парті проходять ефективніше і постійно контролюються сильними учнями. Розсадити учнів по рядах треба так, щоб рівень їх знань і розумового розвитку був наближено однаковим, щоб можливість виграти міг кожен ряд учнів;

6) гра на уроці не повинна проходити стихійно, вона повинна бути чітко організованою і цілеспрямованою. Спочатку учні повинні засвоїти правила гри. Загальні правила повинні бути єдиними для всіх ігор, щоб в учнів поступово виробився стереотип. Крім того, зміст ігри, її форма повинні бути доступними, посильними для учнів.

Правила гри примушують учнів діяти строго по черзі або колективно, відповідати за викликом, уважно слухати відповідь товариша, щоб вчасно виправити його і не повторювати сказаного, бути дисциплінованими, не заважати іншим, чесно погоджуватися із своїми помилками.

Під час ігри вчитель повинен постійно контролювати діяльність учнів, виконання ними правил, спрямовувати гру запитаннями або репліками і непомітно підтримувати дітей, підбадьорювати їх, попереджувати виникнення можливих конфліктів між дітьми, не припускати помилкових дій. Ні в якому разі не можна захоплюватися тільки дидактичною метою гри, недооцінюючи і її виховне значення. Жодне порушення правил не повинно залишитися без уваги вчителя,

В залежності від обставин, він повинен знайти час і досить вимогливо справедливо вказати учню на його недоліки в грі, пояснити до чого призводять подібні вчинки (нечесність, несумлінне відношення до обов'язків) на виробництві, в повсякденному житті. Але під час гри не треба робити довгих зауважень, оскільки це псує настрій учнів, послаблює їх цікавість, гальмує їх увагу.

У грі повинні приймати участь усі учні класу. Тому завдання треб підібрати короткі, посильні, розраховані на відповіді всіх учнів класу.

Слід уникати одноманітності завдань, організовуючи їх таким чином, щоб дітям не треба було довго чекати включення в гру, бо це знижує їх зацікавленість.

Обов’язково треба обговорити, познайомити учнів із загальними правилами для учнів в ході ігри, а саме:

Уважно слухай та запам’ятовуй хід ігри, необхідні дії, їх послідовність.

1.               Пам’ятай, що успіх залежить від чіткого усвідомлення кінцевої мета, передбаченої грою, результат ігри. Не поспішай починати гру, не дослухавши до кінця вказівок вчителя.
2.               Уважно слухай відповідь товариша, щоб при необхідності виправити або доповнити його.
3.               Дочекайся своєї черги, не заважай товаришам, не роби зайвих рухів, будь дисциплінованим.
4.               Чесно визнавай свою помилку, якщо товариші довели, що ти неправий. Помилитися може кожний.
5.               Не хитруй, не шукай легкого нечесного шляху для перемоги, цим ти підводиш товаришів і губиш свій авторитет. Поважають тільки чесних, принципових, вимогливих, справедливих.

Дітей треба попередити і застерегти, що навіть тоді, коли все виконано правильно, але хоча б один з учнів ряду схитрував, то ряд займає останнє місце. Важливо, щоб не тільки вчитель, але і учні слідкували за чесністю дітей в грі.

Елементи гри, змагання, які включені в заняття, здійснюють великий вплив на учнів IV- VIII класів. Ігровий мотив є для них діючим підкріпленням пізнавальнго мотиву, сприяє утворенню додаткових умови для виникнення радощів успіху, задоволеності, почуття колективізму. Для них велике значення мають вдало підібрані ігрові ситуації, наповненні елементами загадковості, таємності. Це особливо характерно для учнів 5-6 класів. Вони з великим задоволенням приймають участь у різних за характером і формою гри. Цікаво при цьому , у учнів більш сильних більшою повагою користуються індивідуальні ігри — змагання на особисту першість, в яких вони можуть показати свої розумові здібності, перевірити свої вольові якості. Слабкі учні, навпаки, залюбки приймають участь у колективних іграх, у яких вони спільно з іншими мають можливість здобути перемогу, відчути радість успіху. Учні цих класів охоче приймають участь у іграх — змаганнях 1 як поміж командами свого класу, так і поміж класів. Ігри та ігрові форми повинні включатися не для того, щоб розважити учнів, а щоб зворушити в них потяг до подолання труднощів.

Мета введення їх полягає в тому , щоб вдало поєднати ігрові і навчальні мотиви і в такій діяльності поступово зробити перехід від ігрових мотивів до навчальних, пізнавальних. Для цього треба так розробити методику ігрових занять, щоб діяльність учнів була ігровою за формою, тобто викликала б ті ж самі емоції', хвилювання, що і гра, але одночасно давала можливість активно добувати необхідні відомості, ліквідувати прогалини в знаннях, сприяла б вихованню пізнавальної діяльності.

Наведу декілька прикладів застосування дидактичних ігор та ігрових ситуацій при вивченні математики в 5-6 класах на різних етапах уроку. Почну з перших уроків 6-го класу. В цьому році мені дали два шостих класи, тому переді мною постало завдання провести перші у роки так, щоб звернути увагу дітей на себе, як на викладача, зацікавити їх математикою, як предметом, щоб у них виникло бажання відвідувати мої уроки. Але, насамперед, перші уроки — повторення того, що вчилося в попередніх класах. Можна просто запропонувати розв’язати ті чи інші вправи, але набагато несподіваніше і цікавіше, для учнів, якщо урізноманітнити форми подачі умови. Для цього можна використати таблиці, схеми, програми, блок - схеми, магічні квадрати, лабіринти, направлені на розвиток логічного мислення, математичної мови, вміння пояснити “що?”, “чому? ”,  “як?”.

Отже, тема перших уроків (а уроки у нас проводяться парами) в 6 - му класі:

«В СВІТІ ТВАРИН»

55,6	66,3	33,6
22,3	22,7	00
33,7	44,1	11,4

 

Частина перша “ Все про бобрів ”

У нашій країні водиться багато бобрів. Бобер — великий гризун, який веде напівводяний спосіб життя, мешкає по лісових річках, споруджує з сухих гілок та мулу будиночки, поперед річок будує греблі довжинною 5 - 6 метрів.

 

 

 

Завдання №1 Визначте довжину тіла бобра (в дециметрах). А допоможе вам дивовижний квадрат (мал. №1)

1.        з першого рядка виберіть найменше число;
2.        з другого рядка виберіть найбільше число рядка
3.        з третього рядка виберіть не найменші і не найбільше;
4.        знайдіть суму трьох чисел — і ви отримаєте відповідь на запитання.

(3,6+2,7+3,7)=10, довжина тіла бобра 10дм. 10дм — скільки це сантиметрів? Порівняйте довжину тіла бобра зі своїм ростом.

 

 

Завдання №2  Визначте, скільки коштують 100 грамів жиру бобра. Відповісти вам допоможе блок — схема

Отже , 100 грамів жиру коштують 200 гр.

- Скільки коштує 1 кілограм жиру бобра?

- Яку частину 100 г. Становить від 1кг?

- Скільки жиру можна купить на 1000 гривень?

Бобри також відмінні плавці та пірнальники, вони декілька хвилин можуть знаходитись під водою.

 

 

 

Завдання №3 В рядках таблиці впишіть назви чисел : 900, 600, 1000, 500, 9. В одному із стовпців прочитайте назву числа, яке вказує, скільки хвилин бобер може знаходитися під водою.

				П	‘	Т	С	О	Т
	Д	Е	В	‘	Я	Т	С	О	Т
Д	Е	В	‘	Я	Т	Ь
				Т	И	С	Я	Ч	А
Ш	І	С	Т	Ь	С	О	Т

- 5 хвилин — скільки це секунд?

- Яку частину 5 — ть хвилин становить від 1 год.?

Частина друга “ чи знаєте ви?”

Найкрупніша наземна тварина — африканський слон. Визначте висоту і довжину тіла (в сантиметрах) африканського слона та його масу  (в кілограмах).

 

 

 

 

 

 

 

 

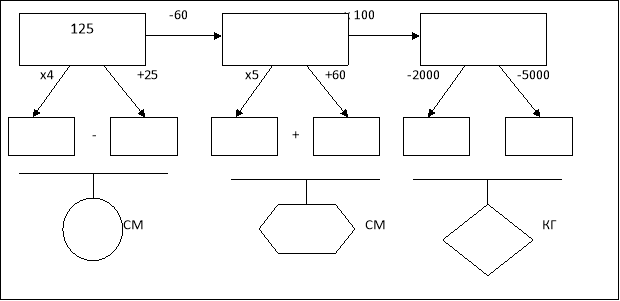
•                   Виразіть висоту і довжину тіла слона в метрах і сантиметрах ,масу тіла в кг.
•                   Поясніть, як від 500 відняти 150,  65 помножити на 5; до 325 додати 125; як помножити на 100?
•                   Маса навантаженого слоненяти в 60 разів менша від маси дорослого слона.| Знайти масу слоненяти.
•                   На скільки кілограмів маса дорослого слона більша маси навантаженого слоненяти?

Наведу ще декілька прикладів використання дидактичних ігор та ігрових ситуацій на різних етапах уроку, під час вивчення різних тем курсу.

 

При закріпленні понять масштаб, середнє арифметичне, побудова трикутників можна провести “Урок - казку”.

За горами, за лісами,

За широкими морями,

Не на небі — на землі,

Жив старий в одному селі.

Було в нього три сина:

Розумний був старший;

Середній так і сяк;

А молодший — ну зовсім ніяк.

Брати сіяли пшеницю

І возили її в столицю.

Напевне, столиця та була

Не дуже далеко від села.

Задача№1

Визначити відстань від села до столиці, якщо відомо, що на карт відстань між цими пунктами 3,7 см. , а масштаб карти 1:50000.

Там пшеницю продавали

Гарні гроші заробляли

 Бо з набитою сумою

Поверталися додому.

Задача№2

Визначити середню врожайність пшениці, яку знімали з полів батько із синами, якщо з першого поля зняли 2,1 ц., з другого 1,9 ц., з третього 1,8 ц., а з четвертого 2,2 ц.

3адача№3

Скільки вони заробили грошей, якщо за один центнер зерна брали        600 грн.?

3адача№4

Накреслити маршрут, за яким їхав Іванушка на конику - горбоконику, якщо відомо, що обручка знаходиться в місті М, терем з сонцем і місяцем в місті К, а сам цар, де відбувалися ці події, живе в місті В. Причому відомо що МВ =  5.3 см (по карті),КМ = 2,5  см, < М = 115°

 

Для формування усних обчислювальних навичок я використовую  так звані « приклади по колу» :

 

1,4+0,6 =				2,6 + 0,4 =
	- 1,7 =				-2,8 =
	*1,2 =				*1,8 =
	: 9 =				: 1,2 =
	+ 0,96 =				+ 0,97 =
	-0,2 =				- 0,1 =
	*5 =				*0,5 =
	:  0,02 =				:0,15 =

 

Віршована задача про кролів і гусей.

В хліві у бабусі

Жили кролі і гуси.

Баба дивною була

Їм рахунок так вела:

Стане вранці на поріг

Підрахує 300 ніг,

А тоді без зайвих слів

Нарахує 100 голів.

Всі на місці.

От і добре,

Можна йти відпочивати.

Відповість хто із дітей

Скільки там було гусей?

Хто зуміє нам сказати:

Скільки там було кроль чат?

Як узагальнюючий контроль над сформованістю навичок виконання дій із натуральними числами, і з десятковими дробами, і із звичайними дробами, можна проводить дидак-тичну гру “Конвеєр"

Для гри готуються карточки , на яких записано по одному зображенню. На початку уроку кожен учень отримує по одній карточці. Він повинен виконати завдання в своєму зошиті і після цього передати карточку товаришу, який сидить за ним. Від сусіда попереду він отримує нову карточку. (На першій парті вчитель кладе не одну, а зразу декілька карточок, щоб  “ конвеєр ” рухався безупинно весь запланований час).  По команді вчителя учні починають виконувати завдання. Вони  працюють напружено і зосередженно, оскільки затримка карточки викликає незадоволення цілої групи учнів, затримуючи карточку, учень затримує роботу всіх, хто сидить позаду нього і тим самим ставить під загрозу програвання всього ряду.

 

Під час вивчення теми «Звичайні дроби. Додавання та віднімання дробів з однаковими знаменниками» . Можна використовувати дидактичну гру «Ланцюжок»

4/11+3/11=	5/11+7/11 =	7/15+11/15= І
1/6+3/6=	11/16-5/16=	5/12+8/12=
41/60-11/60=	19/50+9/50=	11/8-7/8=
11/ 6-5/6=	9/13-6/13=	6/15+1/15=
5/8+5/8=	4/7+5/7=	5/6+3=
10/10-7/10=	41/60-11/60=	19/50-9/50=
1/7+6/7=	4/11+5/11=	5/8+8/8=

 

 

 

 

 

Кожному ряду видається картка, на якій записані нескладні завдання для кожного учня: розв’язати приклад, рівняння, нерівність тощо. Виконавши завдання, учень передає завдання учню, що сидить за ним, останній учень приносить лист до вчителя.

Перемагає той ряд, який давав найбільшу кількість правильних відповідей за найкоротший час. Щоб учень, який розв’язав приклад, не залишався без роботи, можна запропонувати всім “вільним” від роботи приклад на дошці.

Для використання обчислювальних навичок можна запропонувати гру “ Кращий обчислювач ”

Для гри вибирається  “обчислювач”, якому учні пропонують приклади для усного обрахунку до того часу, поки він не зіб’ється; потім його замінював той, хто пропонував останній приклад, і гра продовжується. Перемагав той, хто розв’язав найбільше.

Вдосконалення виконання дій із звичайними і десятковими дробами    можна проводити, використовуючи гру “ П’ятірка ”.

Спочатку умови прикладів дає вчитель, а потім їх складання можна  доручити учням, і це вони зроблять із задоволенням.

Сама гра полягає в тому,  що “5” отримував той учень, який ,виконуючи вказані завдання, перший піднімався по сходинкам як ліворуч, так і праворуч.

 

				5
			-0,11		х10
		+1,53				-0,8
	х5						+0,098
0,36/3								+0,012

 

Під час вивчення теми “ Дільники та кратні ” учні із задоволення приймали участь в змаганнях по рядах, граючи в гру “  Хоп! ”

“ Хоп!”

 

1-й варіант

вчитель пропонує дітям по одному рахувати по порядку від 1,  але замість чисел , які діляться на 2,5,9 тощо, казати “Хоп!”

Той, хто збився, виходить з гри. Можна гру ускладнити, говорячи “Хоп!” замість чисел, кратних 3 і 2, 5 і 3, 2 і 9 одночасно.

 

2-й варіант

вчитель говорить числа в будь - якому порядку, а учні, почувши число, кратне 2 (3,5,9,10,11,4,25 — за домовленістю) плескають у долоні і говорять: “Хоп!”

Наведу декілька прикладів  із завданнями до початку вивчення теми   “Координатна площина ”

Кожен учень отримує дві картки. Одна із завданням, тобто з переліком координат, а друга — з малюнком. Але малюнок не відповідає завданню. Учні виконують малюнки відповідно отриманому набору точок, а готовим малюнком користуються перевіряючи роботу товариша. Оскільки малюнок відповідає зовсім іншому набору точок , учень не може користуватися ним під час своєї роботи. Проте, він використовує готовий малюнок, коли треба порівняти, перевірити роботу товариша. Це також корисна дія. Учень, який тільки що зображував точки по заданим координатам, тепер повинен розв’язати зворотню задачу - за одною точкою знайти її координати. Точки записані в тій послідовності,  в якій їх треба з’єднати. У багатьох випадках перелік починається і закінчується однією і тією ж парою координат, а це означає, що лінія даного фрагменту малюнка повертається в відправну точку. Набори точок перелічені по фрагментах малюнка, тобто точки кожного нового фрагменту записані з нової строки.

Літак:

(-7;0), (-5;2), (7;2),

(9;5), (Ю;5), (10;1), (9;0), (-7;0),

(02), (5;6), (7;6), (4;2),

(0;1), (6;-3), (8;-3), (4;1), (0;1).

Вітрильник:

(0;0),(-10;1),(0;1б),(-1;2),(0;0),

(-9;0), (-8;-1), (-6;-2), (-3;-3) (5;-3), (10;-2), (12;-1),

(13;0), (-9;0),

(0;0), (0;16), (12;2), (0;0).

Людина, яка біжить:

(-8;1), (-б;2), (-2;0), (1;2), (5;1), (7;-4), (9;-3),

(-2;6), (0;8),(3;7), (5;5),(7;7),

(1;2), (3;9), (3;10), (4;11), (5;11), (6;11), (6;9),

(5;8), (4;8), (3;9).

Мухомор:

(-7;0), (-3;9), (-1;11), (1;11), (3;9), (7;0), (5;0), (1;3),

(-1;3),(-5;0),  (7;0),

(1;-9), (2;-8), (2;1), (1;3), (-1;3),(-2;-1),  (-2;-8), (-1;-9), (1;-9),

(-2;-1), (-3;-2), (-2;-2), (0;-2), (1;-3), (2;-2),

(3;-2), (2;-1),

(-2;6), (-2;7), (-1;7), (-1;6) ,

(3;2), (3;3), (4;3), (4;2).

(0;8), (0;9), (1;9), (1;8),

(-5;2), (-5;3), (-4;3), 9-4;20,

(0;4), (0;5), (1;5), (1;4)

Ракета:

(1;5), (0;6), (-1;5), (0;4), (0;-8), (-1;-10), (0;1), (0;-8),

(-4;-б), (-1 ;-10), (0;12), (1;10), (4;-б),

(-3;-6), (-6;-7), (-2;1) (-3;-6),

(2;1), (3;-б), (6;-7), (2;1)

Надалі ,коли діти виконали декілька завдань, вони починають із задоволенням самі складати подібні завдання.

Ось, наприклад, як у п’ятому класі можна проводити фізкультхвилинку.

“Таблипя множення “на пальцях”

Дуже добро, коли такі завдання супроводжуються презентацією, все видно на екрані.

А) Множення па 9:

покладемо руки на парту перед собою, будемо вважати, що кожен палець має свій номер: перший ліворуч - 1, другий - 2, третій - 3 і т.д.

При множенні на 9 піднімаємо той палець, номер якого означає множник. Кількість пальців ліворуч від піднятого означає число десятків добутку, а праворуч - число одиниць. Наприклад, щоб помножити 4 на 9 , піднімаємо четвертий палець. Ліворуч від нього 3 пальці, а праворуч — 6. отже 4*9=36.

Б) Множення чисел, більших від 5:

Нехай нам треба помножити 7 на 8.

На лівій руці, зігнутий в кулак, розгинаємо два пальці (7-5=2), на правій р 3 пальці (8-5=3). Кількість розігнутих пальців на двох руках складемо: 2+3=5. Це десятки добутку. Число зігнутих пальців помножимо: 2*6=6 - це одиниці.

Значить, 7*8=50+6=56

 Аналогічно, 6*8= (1+3)*10+4*2=48

 6*6=(1 + 1)*10+4*4=36.

Безумовно навчання - це велика праця, і не можна будувати уроки тільки на іграх.

Якщо уроки різноманітні і вивчення теоретичного матеріалу переплітається з ігровими ситуаціями, то процес навчання перетворюється для дітей в навчання із захопленням .Навчання із захопленням  - це зовсім не навчання з розвагами. Школа - не цирк, вона не може весь час розважати, вона і не повинна цього робити.

Учитися в школі із захопленням- це означає виховувати в собі почуття обов’язку, вчитися виконувати цей обов’язок з бажанням, з творчим підходом.

Кожному вчителю знайома ситуація, коли оцінки вже виставлені і учні не мають великого бажання працювати. Ось тут і настає черга урокам - жартам, урокам - кросвордам, урокам і казкам, використання ігрових ситуацій та дидактичних ігор.